Найти пересечение двух плоскостей по уравнению

Линия пересечения плоскостей онлайн

С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Линия пересечения плоскостей − теория, примеры и решения

Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α₁ и α₂:

Найдем уравнение линии пересеченя плоскостей α₁ и α₂. Для этого рассмотрим следующие случаи:

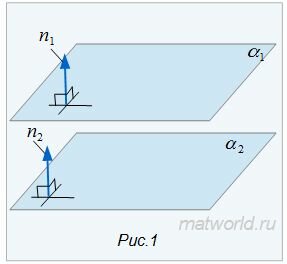Умножив уравнение (2) на λ, получим:

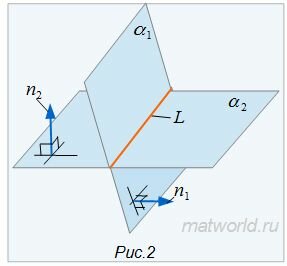Если векторы n₁ и n₂ не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:

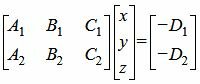(4)

Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.

Так как в системе линейных уравнений (4) векторы n₁=<A₁, B₁, C₁> и n₂=<A₂, B₂, C₂> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:

,

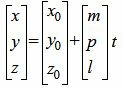(5)

Равенство (5) можно записать в следующем виде:

.

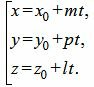(6)

Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α₁ и α₂. Полученное уравнение прямой можно записать в каноническом виде:

.

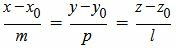Пример 1. Найти линию пересечения плоскостей α₁ и α₂:

Поскольку направляющие векторы n₁ и n₂ неколлинеарны, то плолскости α₁ и α₂ пересекаются.

Для нахождения линии пересечения влоскостей α₁ и α₂ нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:

.

(9)

Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

.

(10)

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 2 со строкой 1, умноженной на −2:

.

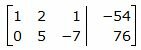Второй этап. Обратный ход Гаусса.

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:

.

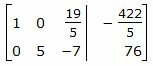Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

.

.

(11)

где t− произвольное действительное число.

Запишем (11) в следующем виде:

.

(12)

Получили уравнение линии пересечения плоскостей α₁ и α₂ в параметрическом виде. Запишем ее в каноническом виде.

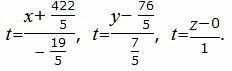(13)

Из равентсв выше получим каноническое уравнение прямой:

Ответ. Уравнение линии пересечения плоскостей α₁ и α₂имеет вид:

Пример 2. Найти линию пересечения плоскостей α₁ и α₂:

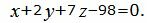(14)

(15)

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/2), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/2:

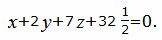(16)

Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α₁ и α₂ не совпадают. Следовательно они параллельны, т.е. не пересекаются.

Пример 3. Найти линию пересечения плоскостей α₁ и α₂:

(17)

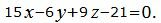(18)

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/3), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/3:

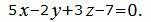(19)

Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α₁ и α₂ совпадают.

Как найти прямую пересечения двух плоскостей

С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Линия пересечения плоскостей − теория, примеры и решения

Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α₁ и α₂:

Найдем уравнение линии пересеченя плоскостей α₁ и α₂. Для этого рассмотрим следующие случаи:

Умножив уравнение (2) на λ, получим:

Если векторы n₁ и n₂ не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:

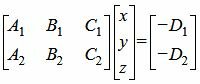(4)

Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.

Так как в системе линейных уравнений (4) векторы n₁= и n₂= не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:

,

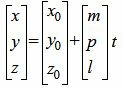(5)

Равенство (5) можно записать в следующем виде:

.

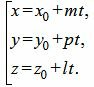(6)

Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α₁ и α₂. Полученное уравнение прямой можно записать в каноническом виде:

.

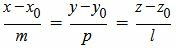Пример 1. Найти линию пересечения плоскостей α₁ и α₂:

Поскольку направляющие векторы n₁ и n₂ неколлинеарны, то плолскости α₁ и α₂ пересекаются.

Для нахождения линии пересечения влоскостей α₁ и α₂ нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:

.

(9)

Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

.

(10)

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 2 со строкой 1, умноженной на −2:

.

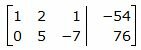Второй этап. Обратный ход Гаусса.

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:

.

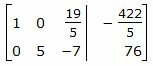Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

.

.

(11)

где t− произвольное действительное число.

Запишем (11) в следующем виде:

.

(12)

Получили уравнение линии пересечения плоскостей α₁ и α₂ в параметрическом виде. Запишем ее в каноническом виде.

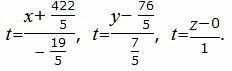(13)

Из равентсв выше получим каноническое уравнение прямой:

Ответ. Уравнение линии пересечения плоскостей α₁ и α₂имеет вид:

Пример 2. Найти линию пересечения плоскостей α₁ и α₂:

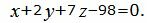(14)

(15)

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/2), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/2:

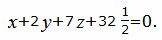(16)

Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α₁ и α₂ не совпадают. Следовательно они параллельны, т.е. не пересекаются.

Пример 3. Найти линию пересечения плоскостей α₁ и α₂:

(17)

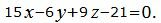(18)

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/3), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/3:

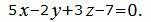(19)

Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α₁ и α₂ совпадают.

Пусть в канонических уравнениях прямой

коэффициент отличен от нуля, т. е. прямая не параллельна плоскости хОу. Запишем эти уравнения раздельно в таком виде:

При нашем условии уравнения (6) вполне определяют прямую. Каждое из них в отдельности выражает плоскость, причем первая из них параллельна оси Оу, а вторая — оси

Таким образом, представляя прямую линию уравнениями вида (6), мы рассматриваем ее как пересечение двух плоскостей, проектирующих эту прямую на плоскости координат xOz и yOz. Первое из уравнений (6), рассматриваемое в плоскости определяет проекцию данной прямой линии на эту плоскость; точно так же второе из уравнений (6), рассматриваемое в плоскости определяет проекцию данной прямой линии на плоскости yOz. Итак, можно сказать, что дать уравнения прямой линии в виде (6) — это значит дать ее проекции на плоскости координат хOz и yOz.

Если бы направляющий коэффициент был ранен нулю, то обязательно хотя бы один из двух других коэффициентов, например , был бы отличен от нуля, т. е. прямая не была бы параллельна плоскости yOz. В этом случае мы могли бы выразить прямую

уравнениями плоскостей, проектирующих ее на координатные плоскости записав уравнения (5) в виде

Таким образом, любая прямая может быть выражена уравнениями двух плоскостей, проходящих через нее и проектирующих ее на координатные плоскости. Но определять прямую совсем не обязательно именно такой парой плоскостей.

Через каждую прямую проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно, представляют собой уравнения этой прямой.

Вообще всякие две не параллельные между собой плоскости с общими уравнениями

определяют прямую их пересечения.

Уравнения (7), рассматриваемые совместно, называются общими уравнениями прямой.

От общих уравнений прямой (7) можно перейти к ее каноническим уравнениям. Для этой цели мы должны знать какую-нибудь точку прямой и направляющий вектор.

Координаты точки легко найдем из данной системы уравнений, выбирая одну из координат произвольно и решая после этого систему двух уравнений втносителыю оставшихся двух координат.

Для отыскания направляющего вектора прямой заметим, что этот вектор, направленный по линии пересечения данных плоскостей, должен быть перпендикулярным к обоим нормальным векторам этих плоскостей. Обратно, всякий вектор, перпендикулярный к параллелен обеим плоскостям, а следовательно, и данной прямой.

Но векторное произведение также обладает этим свойством. Поэтому за направляющий вектор прямой можно принять векторное произведение нормальных векторов данных плоскостей.

Пример 1. Привести к каноническому виду уравнения прямой

Выберем произвольно одну из координат. Пусть, иапример, . Тогда

откуда Итак, мы нашли точку (2, 0, 1), лежащую на прямой,

Находя теперь векторное произведение векторов получаем направляющий вектор прямой Поэтому канонические уравнения будут:

Замечание. От общих уравнений прямой вида (7) можно перейти к каноническим, и не прибегая к векторному методу.

Предварительно остановимся несколько подробнее на уравнениях

Выразим из них х и у через . Тогда получим:

Уравнения (6) называются уравнениями прямой в проекциях на плоскости

Установим геометрический смысл постоянных М и N: М представляет собой угловой коэффициент проекции данной прямой на плоскость координат (тангенс угла этой проекции с осью Oz), а N есть угловой коэффициент проекции данной прямой на плоскость координат (тангенс угла этой проекции с осью Oz). Таким образом, числа определяют направления проекций данной прямой линии на две плоскости координат, а значит, они характеризуют и направление самой данной прямой. Поэтому числа М и N называют угловыми коэффициентами данной прямой.

Чтобы выяснить геометрический смысл постоянных положим в уравнениях (6) прямой линии тогда получим: т. е. точка лежит на данной прямой. Очевидно, эта точка есть точка пересечения данной прямой с плоскостью Итак, суть координаты следа данной прямой линии на плоскости координат

Теперь легко сделать переход от уравнений в проекциях к каноническим. Пусть, например, даны уравнения (6). Решая эти уравнения относительно , найдем:

откуда непосредственно получаем канонические уравнения в виде

Пример 2. Привести канонические уравнения прямой

к уравнениям в проекциях на плоскости

Данные уравнения переписываем в виде

Решая первое из этих уравнений относительно х, а второе относительно у, найдем искомые уравнения в проекциях:

Пример 3. Привести уравнения в ппоекциях

к каноническому виду.

Решая данные уравнения относительно , получим:

Пример 4. Принести уравнения в проекциях

к каноническому виду.

Переписав систему уравнений в виде

Уравнения в проекциях можно получить и из общих уравнений прямой (7), решая общие уравнения относительно каких-нибудь двух координат, например х и у, если прямая параллельна плоскости хОу, то привести уравнения (7) к уравнениям (6) не удастся, но тогда можно привести уравнения (7) к уравнениям в проекциях на другую пару координатных плоскостей.

Если требуется общие уравнения прямой привести к каноническим, то можно предварительно перейти к уравнениям в проекциях.

Пример 5. Привести уравнения прямой

к каноническому виду.

Решая данные уравнения относительно х и у, найдем уравнения в проекциях

Выражаем из этих уравнений :

и получаем каноническне уравнения

Умножив каждым из направляющих коэффициентов на — 5, получим более простой вид канонических уравнений:

1. Взаимное расположение двух плоскостей.

Если две плоскости пересекаются, то система линейных уравнений задаёт уравнение прямой в пространстве.

То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:

Записать канонические уравнения прямой

Решение: Чтобы составить канонические уравнения прямой, необходимо знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….

1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? В системе уравнений нужно обнулить какую-нибудь координату. Пусть 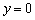, тогда получаем систему двух линейных уравнений с двумя неизвестными: . Почленно складываем уравнения и находим решение системы:

Таким образом, точка принадлежит данной прямой. Обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует проводить мысленно или на черновике.

Выполним проверку: подставим координаты точки в исходную систему уравнений: . Получены верные равенства, значит, действительно .

2) Как найти направляющий вектор прямой? Его нахождение наглядно демонстрирует следующий схематический чертёж:

Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей. А если , то вектор «пэ» найдём как векторное произведение векторов нормали: .

Из уравнений плоскостей снимаем их векторы нормали:

И находим направляющий вектор прямой:

Как проверить результат, рассматривалось в статье Векторное произведение векторов.

3) Составим канонические уравнения прямой по точке и направляющему вектору :

Ответ:

На практике можно пользоваться готовой формулой: если прямая задана пересечением двух плоскостей , то вектор является направляющим вектором данной прямой.

Записать канонические уравнения прямой

Это пример для самостоятельного решения. Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения и подставьте в моё уравнение (или наоборот).

Полное решение и ответ в конце урока.

Во второй части урока мы рассмотрим взаимное расположению прямых в пространстве, а также разберём задачи, которые связаны с пространственными прямыми и точками. Терзают меня смутные ожидания, что материала будет прилично, поэтому лучше всё-таки сделать отдельную веб страницу.

Добро пожаловать: Задачи с прямой в пространстве >>>

Решения и ответы:

Пример 4: Ответы:

Пример 6: Решение: Найдём направляющий вектор прямой:

Уравнения прямой составим по точке 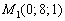и направляющему вектору :

Ответ: («игрек» – любое)

Пример 8: Решения и ответы:

в) Найдём направляющий вектор прямой: . Параметрические уравнения прямой составим по точке (можно выбрать точку «бэ») и направляющему вектору :

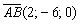
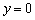
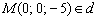
Пример 10: Решение: Найдём какую-нибудь точку, принадлежащую данной прямой. Пусть , тогда: . Точка . Найдём направляющий вектор прямой, используем формулу:

Составим канонические уравнения прямой по точке и направляющему вектору :

Ответ:

Дата добавления: 2015-05-10 ; Просмотров: 3974 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

5.4.4. Прямая, заданная пересечением двух плоскостей

Если плоскости пересекаются, то система линейных уравнений задаёт прямую в пространстве.

То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:

Задача 151

Записать канонические уравнения прямой

Решение: чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….

1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? Методом подбора. В системе уравнений обнулим какую-нибудь координату, например, . Тогда получается система двух линейных уравнений с двумя неизвестными: . Почленно складываем уравнения и находим решение системы:

Таким образом, точка принадлежит данной прямой. Но принадлежит ли? Выполним проверку – подставим её координаты в исходную систему уравнений:

Получены верные равенства, значит, действительно .

В процессе подбора обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует проводить мысленно или на черновике.

2) Как найти направляющий вектор прямой? Существует готовая формула: если прямая задана пересечением двух плоскостей , то вектор является направляющим вектором данной прямой.
В нашей задаче:

Однако всех формул не упомнишь и поэтому очень важно понимать, откуда они взялись. Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей: и , поэтому вектор «пэ» можно найти как векторное произведение векторов нормали: .
Из уравнений плоскостей «снимаем» их векторы нормали:
и находим направляющий вектор прямой:

Проверим результат с помощью скалярного произведения:
, ч.т.п.

И, наконец, завершающий этап:

3) Составим канонические уравнения прямой по точке и направляющему вектору :

Ответ:

Аналогичная задача для самостоятельного решения:

Задача 152

Записать канонические уравнения прямой

Будьте внимательны! Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения и подставьте в моё уравнение (или наоборот).

Полное решение и ответ в конце книги.

И сейчас самое время перейти к простейшим задачам с пространственной прямой: