Найти площадь поверхности заданной уравнением

Вычисление площади поверхности

Вычисление площади поверхности

1. Услуги проектирования
2. Двойной интеграл
3. Вычисление площади поверхности

Вычисление площади поверхности

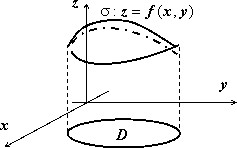
Пусть в пространстве задана кусочно-гладкая поверхность $\sigma $, однозначно проектирующаяся в область $\mathbf < \textit < D >> $ на плоскости $\mathbf < \textit < Оху >> $. Пусть эта поверхность задаётся уравнением $\sigma :\;z=f(x,y),\;(x,y)\in D$. Тогда площадь этой поверхности выражается формулой

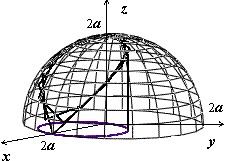
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >$ = 2$\mathbf < \textit < ax >> $ из сферы $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >$ = 4$\mathbf < \textit < a >> ^ < 2 >$ .

Решение:

Область $\mathbf < \textit < D >> $ — сдвинутый на $\mathbf < \textit < а >> $ единиц по оси $\mathbf < \textit < Ох >> $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $\mathbf < \textit < Оху >> $ и $\mathbf < \textit < Охz >> $:

Вычислить площадь cферы радиуса (a.)

Решение:

Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ < < x^2 >+ < y^2 >+ < z^2 >= < a^2 >> \;\; < \text < или >\;\;z = \sqrt < < a^2 >— < x^2 >— < y^2 >> . > $

Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ < S_ < \large\frac < 1 > < 2 >\normalsize > > = \iint\limits_R < \sqrt < 1 + < < \left( < \frac < < \partial z >> < < \partial x >> >\right) > ^2 > + < < \left( < \frac < < \partial z >> < < \partial y >> >\right) > ^2 > > dxdy > .$

Площадь поверхности полной сферы, соответственно, равна $S = 2 < S_ < \large\frac < 1 > < 2 >\normalsize > > = 4\pi < a^2 >.$

Далее:

Вычисление площадей плоских областей

Определение двойного интеграла

Специальные векторные поля

Поверхностный интеграл первого рода и его свойства

Вычисление объёмов

Определение криволинейного интеграла второго рода

Вычисление криволинейного интеграла второго рода. Примеры.

Поверхностный интеграл второго рода и его свойства

Критерий полноты <формулировка>. Лемма о нелинейной функции

Частные случаи векторных полей

Критерий полноты <формулировка>. Лемма о немонотонной функции

Вычисление двойного интеграла

Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

Примеры применения цилиндрических и сферических координат

Огравление $\Rightarrow $

Как найти площадь поверхности вращения с помощью интеграла

Прежде чем перейти к формулам площади поверхности вращения, дадим краткую формулировку самой поверхности вращения. Поверхность вращения, или, что то же самое — поверхность тела вращения — пространственная фигура, образованная вращением отрезка AB кривой вокруг оси Ox (рисунок ниже).

Представим себе криволинейную трапецию, ограниченную сверху упомянутым отрезком кривой. Тело, образованное вращением этой трапеции вокруг то же оси Ox, и есть тело вращения. А площадь поверхности вращения или поверхности тела вращения — это его внешняя оболочка, не считая кругов, образованных вращением вокруг оси прямых x = a и x = b .

Заметим, что тело вращения и соответственно его поверхность могут быть образованы также вращением фигуры не вокруг оси Ox, а вокруг оси Oy.

Вычисление площади поверхности вращения, заданной в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая, вращением которой вокруг координатной оси образовано тело вращения.

Формула для вычисления площади поверхности вращения следующая:

(1).

Пример 1. Найти площадь поверхности параболоида, образованную вращением вокруг оси Ox дуги параболы , соответствующей изменению x от x = 0 до x = a .

Решение. Выразим явно функцию, которая задаёт дугу параболы:

Найдём производную этой функции:

Прежде чем воспользоваться формулу для нахождения площади поверхности вращения, напишем ту часть её подынтегрального выражения, которая представляет собой корень и подставим туда найденную только что производную:

Далее по формуле (1) находим:

Ответ: длина дуги кривой равна

.

Пример 2. Найти площадь поверхности, образуемой вращением вокруг оси Ox астроиды .

Решение. Достаточно вычислить площадь поверхности, получающейся от вращения одной ветви астроиды, расположенной в первой четверти, и умножить её на 2. Из уравнения астроиды выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности вращения:

.

Производим интегрирование от 0 до a:

Ответ: площадь поверхности вращения равна .

Вычисление площади поверхности вращения, заданной параметрически

Рассмотрим случай, когда кривая, образующая поверхность вращения, задана параметрическими уравнениями

Тогда площадь поверхности вращения вычисляется по формуле

(2).

Пример 3. Найти площадь поверхности вращения, образованной вращением вокруг оси Oy фигуры, ограниченной циклоидой и прямой y = a . Циклоида задана параметрическими уравнениями

Решение. Найдём точки пересечения циклоиды и прямой. Приравнивая уравнение циклоиды и уравнение прямой y = a , найдём

Из этого следует, что границы интегрирования соответствуют

Теперь можем применить формулу (2). Найдём производные:

Запишем подкоренное выражение в формуле, подставляя найденные производные:

Найдём корень из этого выражения:

.

Подставим найденное в формулу (2):

.

И, наконец, находим

В преобразовании выражений были использованы тригонометрические формулы

Ответ: площадь поверхности вращения равна .

Вычисление площади поверхности вращения, заданной в полярных координатах

Пусть кривая, вращением которой образована поверхность, задана в полярных координатах:

Площадь поверхности вращения вычисляется по формуле:

(3).

Пример 4. Найти площадь поверхности, образованной вращением лемнискаты вокруг полярной оси.

Решение. Действительные значения для ρ получаются при , то есть при (правая ветвь лемнискаты) или при (левая ветвь лемнискаты).

Решение. Дифференциал корня из формулы площади поверхности вращения равен:

В свою очередь произведение функции, которой задана лемниската, на синус угла равно

.

Поэтому площадь поверхности вращения найдём следующим образом:

.

Вычисление площади поверхности с помощью двойного интеграла

Вы будете перенаправлены на Автор24

Основные формулы

Если везде в области $D$ на координатной плоскости $xOy$ для формулы $I=\iint \limits _f\left(x,y\right)\cdot dx\cdot dy $ положить $f\left(x,y\right)\equiv 1$, то, в соответствии со своим геометрическим смыслом, двойной интеграл будет численно равен площади $S$ области интегрирования $D$, то есть $S=\iint \limits _dx\cdot dy $. В полярной системе координат эта же самая формула приобретает вид $S=\iint \limits _ >\rho \cdot d\rho \cdot d\phi $.

Пусть некоторая поверхность $Q$ задана уравнениям $z=f_ <1>\left(x,y\right)$. Вычислим площадь той части поверхности $Q$, которая проецируется на координатную плоскость $xOy$ в область $D_ <1>$, где функция $f_ <1>\left(x,y\right)$ непрерывна и имеет непрерывные частные производные. Тогда искомую площадь можно вычислить по формуле $S=\iint \limits _ >\sqrt<1+\left(\frac<\partial z> <\partial x>\right)^ <2>+\left(\frac<\partial z> <\partial y>\right)^ <2>> \cdot dx\cdot dy $.

Если уравнение поверхности $Q$ задано в виде $x=f_ <2>\left(y,z\right)$ или $y=f_ <3>\left(x,z\right)$, то соответствующие формулы для вычисления площади поверхности имеют следующий вид:

Здесь $D_ <2>$ и $D_ <3>$ — области, в которые проецируется поверхность $Q$ на координатные плоскости $yOz$ и $xOz$ соответственно.

Применение формул на практике

Находим координаты точки $B\left(x_ ,y_ \right)$:

$y_ =2\cdot x_^ <2>-16\cdot x_ +31=2\cdot 6^ <2>-16\cdot 6+31=7$. Получаем $B\left(6,7\right)$.

Готовые работы на аналогичную тему

На горизонтальной плоскости $xOy$ находится вертикальное цилиндрическое сооружение. Пол сооружения (область $D$) имеет вид прямоугольника с вершинами $O\left(0,0\right)$, $M\left(5,0\right)$, $K\left(5,7\right)$ и $N\left(0,7\right)$. Крыша сооружения имеет вид купола и описывается уравнением $z=\sqrt <\left(4\cdot x+5\right)^<3>> +\sqrt <\left(2\cdot y+6\right)^<3>> $. Требуется с помощью двойного интеграла вычислить площадь крыши этого сооружения.

Его прямоугольный пол является правильным в направлении оси $Oy$. Прямые $x=a$ и $x=b$ ограничивают пол в направлении оси $Ox$ сзади и спереди, следовательно, $a=0$, $b=5$. Линии $\phi _ <1>\left(x\right)$ и $\phi _ <2>\left(x\right)$ ограничивают пол в направлении оси $Oy$ слева и справа, следовательно, $\phi _ <1>\left(x\right)=0$, $\phi _ <2>\left(x\right)=7$. Окончательно $S=\int \limits _<0>^<5>dx\cdot \int \limits _<0>^<7>\sqrt<1+\left(\frac<\partial z> <\partial x>\right)^ <2>+\left(\frac<\partial z> <\partial y>\right)^ <2>> \cdot dy $.

Таким образом, для нахождения площади нужно вычислить интеграл

\[S=\int \limits _<0>^<5>dx \int \limits _<0>^<7>\sqrt \cdot dy =\int \limits _<0>^<5>dx \int \limits _<0>^<7>\sqrt <144\cdot x+18\cdot y+235>\cdot dy .\]