Приближенное нахождение корней уравнения
Задание 2 . 1) Выбрав стартовую точку с координатами x01=0.5 и xo2=0.4, примените метод Ньютона–Рафсона, и с точностью e=0.000001 найдите минимум целевой функции:
Скачать решение
2) Выбрав ту же стартовую точку, примените метод наискорейшего спуска, и вновь найдите минимум целевой функции с точностью e=0.0001.
Пример №1 . Отделить корни аналитически и уточнить один из них методом половинного деления с точностью до 0,01.
Решение.
sin(x+3.14/3)-x/2=0. Скачать
Пример №2 . Определить и найти действительные корни с точностью до 0,001: а) x 4 – 2x – 1 = 0 — методами: 1) деления отрезка пополам; 2) касательных. б) 2log(x) — (x-2) 2 = 0 — методами: 1) хорд; 2) итераций.
Решение.
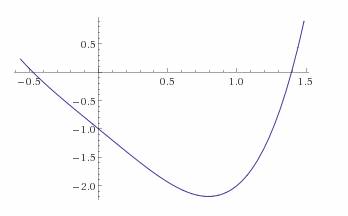
Найдем корни уравнения:
x 4 -2•x-1 = 0
Используем для этого Метод половинного деления (метод дихотомии).
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [-1;2] разобьем на 10 подынтервалов.
h1 = -1 + 1*(2-(-1))/10 = -0.7
h2 = -1 + (1+1)*(2-(-1))/10 = -0.4
Поскольку F(-0.7)*F(-0.4) 0, то a=-0.55
Итерация 2.
Находим середину отрезка: c = (-0.55 -0.4)/2 = -0.48
F(c) = 0.000907
F(x) = 0.19
Поскольку F(c)•F(x) > 0, то a=-0.48
Итерация 3.
Находим середину отрезка: c = (-0.48 -0.4)/2 = -0.44
F(c) = -0.0884
F(x) = 0.000907
Поскольку F(c)•F(x) 0, то a=1.25
Итерация 2.
Находим середину отрезка: c = (1.25 + 1.4)/2 = 1.33
F(c) = -0.57
F(x) = -1.06
Поскольку F(c)•F(x) > 0, то a=1.33
Итерация 3.
Находим середину отрезка: c = (1.33 + 1.4)/2 = 1.36
F(c) = -0.28
F(x) = -0.57
Поскольку F(c)•F(x) > 0, то a=1.36
Итерация 4.
Находим середину отрезка: c = (1.36 + 1.4)/2 = 1.38
F(c) = -0.12
F(x) = -0.28
Поскольку F(c)•F(x) > 0, то a=1.38
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 1.25 | 1.1 | 1.4 | -1.06 | -1.06 |
| 2 | 1.33 | 1.25 | 1.4 | -0.57 | -0.57 |
| 3 | 1.36 | 1.33 | 1.4 | -0.28 | -0.28 |
| 4 | 1.38 | 1.36 | 1.4 | -0.12 | -0.12 |
| 5 | 1.39 | 1.38 | 1.4 | -0.0415 | -0.0415 |
| 6 | 1.4 | 1.39 | 1.4 | -0.000217 | -0.000217 |
| 7 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0206 |
| 8 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0102 |
| 9 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.00498 |
Ответ:
x = 1.4; F(x) = 0.00498
Количество итераций, N = 9
Параметр сходимости.
α = (1.4 — 1.4)/9 = 6.5E-5
Посмотрите как можно быстро решить задачу.
Метод Ньютона онлайн
Данный онлайн калькулятор находит корень уравнения приближённо. В основе алгоритма его работы лежит метод Ньютона. Чтобы начать работу, необходимо ввести исходные данные своей задачи.
Методом Ньютона, найти корень (
максимальное кол-во итераций:
критерий останова вычислений:
Метод Ньютона является численным, т.е. корень уравнения находится приближенно. При этом можно заранее задать точность его нахождения.
Пусть нам дано уравнение
Формула для поиска корня уравнения выглядит следующим образом:
и — приближённые значения корня уравнения на -ой и ( )-ой итерациях соответственно, — значение функции в точке , — значение производной функции в точке .
Как видно, для того чтобы начать работу необходимо задать точку — начальное приближение для корня уравнения . От выбора точки зависит сойдётся ли алгоритм к решению или нет. Сходимость метода квадратичная, но она резко ухудшается если мы ищем кратный корень уравнения, т.е. если и одновременно , где — кратный корень уравнения .
Вычисления по приведённой выше формуле можно продолжать до бесконечности, соответственно на практике необходим некоторый критерий, который будет определять нужно ли нам продолжать вычисления или нет. Как правило, используется критерий останова вычислений на основе приращения или же на основе близости функции к нулю в некоторой точке .
Критерий останова вычислений на основе приращения задаётся следующей формулой:
т.е. различие (по модулю) между двумя последовательными приближениями к корню уравнения ( и ) должны быть меньше, некоторой наперёд заданной величины .
Критерий останова вычислений на основе близости функции к нулю определяется следующей формулой:
т.е. отличие (по модулю) между функцией в некоторой точке и нулём меньше .
В тоже время, если последовательность к корню не сходится, то критерии останова не сработают и процесс поиска корня будет продолжаться бесконечно. Чтобы предотвратить такую ситуацию, на практике вычисления прекращают после некоторого, заданного количества итераций.
На рисунке ниже приведена геометрическая интерпретация процесса поиска корня уравнения методом Ньютона.
В точке мы строим касательную к графику функции . Уравнение касательной в этой точке имеет вид:
Находим точку пересечения полученной касательной с осью абсцисс, т.е. рассматриваем точку с координатами . Подставляя координаты указанной точки в уравнение касательной, получаем следующее соотношение:
Из данного уравнения находим :
Продолжая данный процесс, получим формулу метода Ньютона, приведенную выше. Из-за того, что на каждой итерации фактически происходит построение касательной, метод Ньютона также иногда называют методом касательных.
Другие полезные разделы:
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
Численные методы решения нелинейных уравнений
В этом разделе приведены примеры решенных задач по теме нахождения корней нелинейных уравнений численными методами. На первом этапе обычно происходит локализация (отделение) корней (графически или аналитически), на втором — уточнение (поиск) корней разными методами: Ньютона, Стеффенсена, секущих, хорд, касательных, простой итерации.
Примеры приближенных решений нелинейных уравнений онлайн
Задача 1. Методом бисекции найти решение нелинейного уравнения на отрезке $[a;b]$ с точностью $\varepsilon = 10^<-2>$. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью $\varepsilon=10^<-4>$. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
Задача 2. Отделить корни нелинейного уравнения аналитически $2 arcctg x -x+3=0$.
Задача 3. Отделить корни нелинейного уравнения аналитически и уточнить один из них методом проб с точностью до 0,01. $$3x^4-8x^3-18x^2+2=0.$$
Задача 4. Отделить корни нелинейного уравнения графически (например, в среде EXCEL) уточнить один из них методом проб с точностью до 0,01. $$x^2-20 \sin x =0.$$
Задача 5. Отделите корни уравнения графически и уточните один из них методом хорд с точностью до 0,001. Уточните один из корней этого уравнения методом касательных с точностью до 0,001. $$ \sqrt
Задача 6.Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. $$\sqrt
Задача 7. На отрезке $[0;2]$ методом Ньютона найти корень уравнения $-x^3-2x^2-4x+10=0$ с точностью 0,01.
Задача 8. Методом хорд найти отрицательный корень уравнения $x^3-2x^2-4x+7=0$ с точностью 0,0001. Требуется предварительное построение графика функции и отделение корней.
Задача 9. Решить нелинейные уравнения с точностью до 0.001. $$1)\, x^3-12x-5=0\, (x \gt 0), \, 2)\, \tan x -1/x=0. $$
http://mathforyou.net/online/numerical/newton/
http://www.matburo.ru/ex_cm.php?p1=cmnu