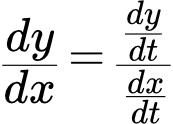Найти производную функции заданной параметрическими уравнениями

Производная функции заданной параметрически онлайн

Пусть функция задана в виде параметрических уравнений (т.н. параметрическое задание функции):

где x ( t ) , y ( t ) — дифференцируемые функции и x ‘ ( t ) ≠ 0 . Тогда производная

определяется по формуле:

где — производная от параметрического уравнения y ( t ) по параметру t и — производная от параметрического уравнения x ( t ) , по параметру t .

Наш онлайн сервис найдет производную от параметрической функции с подробным решением. Пример подробного решения, выдаваемого нашим сервисом, можно посмотреть здесь .

Производная параметрической функции

Результат

Примеры производных функции, заданной параметрически

• Степенные функции
• Тригонометрические функции

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Производная функции, заданной параметрическим способом

Формула производной

Пусть функция задана параметрическим способом:
(1)
где некоторая переменная, называемая параметром. И пусть функции и имеют производные при некотором значении переменной . Причем и функция имеет обратную функцию в некоторой окрестности точки . Тогда функция (1) имеет в точке производную , которая, в параметрическом виде, определяется по формулам:
(2)

Здесь и – производные функций и по переменной (параметру) . Их часто записывают в следующем виде:
;
.

Тогда систему (2) можно записать так:

Доказательство

По условию, функция имеет обратную функцию. Обозначим ее как
.
Тогда исходную функцию можно представить как сложную функцию:
.
Найдем ее производную, применяя правила дифференцирования сложной и обратной функций:
.

Доказательство вторым способом

Найдем производную вторым способом, исходя из определения производной функции в точке :
.
Введем обозначение:
.
Тогда и предыдущая формула принимает вид:
.

Воспользуемся тем, что функция имеет обратную функцию , в окрестности точки .
Введем обозначения:
; ;
; .
Разделим числитель и знаменатель дроби на :
.
При , . Тогда
.

Производные высших порядков

Чтобы найти производные высших порядков, надо выполнять дифференцирование несколько раз. Допустим, нам надо найти производную второго порядка от функции, заданной параметрическим способом, следующего вида:
(1)

По формуле (2) находим первую производную, которая также определяется параметрическим способом:
(2)

Обозначим первую производную, посредством переменной :
.
Тогда, чтобы найти вторую производную от функции по переменной , нужно найти первую производную от функции по переменной . Зависимость переменной от переменной также задана параметрическим способом:
(3)
Сравнивая (3) с формулами (1) и (2), находим:

Теперь выразим результат через функции и . Для этого подставим и применим формулу производной дроби:
.
Тогда
.

Отсюда получаем вторую производную функции по переменной :

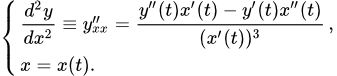
Она также задана в параметрическом виде. Заметим, что первую строку также можно записать следующим образом:
.

Продолжая процесс, можно получить производные функции от переменной третьего и более высоких порядков.

Заметим, что можно не вводить обозначение для производной . Можно записать так:
;
.

Пример 1

Найдите производную от функции, заданной параметрическим способом:

Пример 2

Найдите производную от функции, выраженной через параметр :

Раскроим скобки, применяя формулы для степенных функций и корней:
.

Находим производную . Для этого введем переменную и применим формулу производной сложной функции.

.

Находим искомую производную:
.

Пример 3

Найдите производные второго и третьего порядков от функции, заданной параметрическим способом в примере 1:

В примере 1 мы нашли производную первого порядка:

Введем обозначение . Тогда функция является производной по . Она задана параметрическим способом:

Чтобы найти вторую производную по , нам надо найти первую производную по .

Дифференцируем по .
.
Производную по мы нашли в примере 1:
.
Производная второго порядка по равна производной первого порядка по :
.

Итак, мы нашли производную второго порядка по в параметрическом виде:

Теперь находим производную третьего порядка. Введем обозначение . Тогда нам нужно найти производную первого порядка от функции , которая задана параметрическим способом:

Производная третьего порядка по равна производной первого порядка по :
.

Замечание

Можно не вводить переменные и , которые являются производными и , соответственно. Тогда можно записать так:
;
;
;
;
;
;
;
;
.

В параметрическом представлении, производная второго порядка имеет следующий вид:

Производная третьего порядка:

Автор: Олег Одинцов . Опубликовано: 22-01-2017