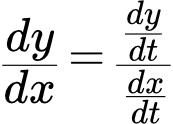Найти производную по параметру дифференциальные уравнения

Дифференцируемость решения по параметру и ее применения по начальным условиям

По этой ссылке вы найдёте полный курс лекций по математике:

Рассматривается система уравнений с параметром ц При каждом /i система имеет решение. Оно зависит не только от ty но и от выбранного значения параметра поэтому обозначается x(t, р). Теорема 1. Пусть при — область в Rn+I, М — интервал в R1) все функции a'(fi) непрерывны. Пусть при всех ft € М на отрезке t2] Э t0 решение x(t,p) задачи (1) существует и проходит в области D. Тогда это решение имеет производные dxjdp, непрерывные по (;t, ц).

Функции V4 = Qxjdp. (i = 1. п) удовлетворяют системе уравнений в вариациях В (2) производные от /• зависят от аргументов J, «j /i). xn(t9fi)9fi9 где — координаты решения /*) при том значении при котором разыскивается дх/др. Если решение x(t, ц) известно хотя бы при одном значении д, то система^!), позволяет найти дх/дц при этом ft. Систему (2) можно не запоминать, она получается посредством дифференцирования обеих частей системы (1) по \l\ при этом считаем, что х = x(t, /х), и дх

Найти дх/дц при \l — 0 от решения задачи Дифференцируемость решения по параметру и ее применения по начальным условиям. Решение примера. Условия теоремы 1 выполнены, так как функции / = х2 + 4fit р? и a(fi) = 2/i — 1 непрерывны и имеют непрерывные производные по х и ц. Дифференцируя (3) по ц и обозначая х^ = и, получаем Здесь \i = 0, а х — решение задачи (3) при ц = О, то есть задачи dx/dt = ж2, ж(1) = -1. Отсюда а: = -1 ft.

Теперь (4) принимает вид Решая это линейное уравнение (выкладки пропускаем), получаем и = t2 + d

2. Из начального условия находим с = 1. Итак, Доказательство теоремы. Зафиксируем /х € М. Имеем где — решение задачи (1), но с Д вместо ji, то есть Обозначим дробь в (5) через Д). Идея доказательства теоремы. Составляем дифференциальное уравнение для v(t9 Д) при Д Ф fi.

Его правая часть при Д /х стремится к правой части уравнения (2).

Поэтому и решение v(t9 Д) при Д /х, то есть дробь в (5), стремится к решению уравнения (2). Значит, предел в (5), то есть дх/дц9 существует и удовлетворяет уравнению (2). Из уравнений (6) и (1), вычитая и деля на Д — р, получаем Преобразуем первую дробь в (7). Положим Тогда Поэтому из (7) имеем Так как df/dx, df/Зц непрерывны по совокупности переменных, то подынтегральные функции непрерывны по , а интегралы непрерывно по t. Из (6) по теореме 7 §7 ж непрерывно по (;t, Д) — по совокупности переменных.

Поэтому последние два интеграла в (8) — непрерывные функции от Д), включая значение Д = Обозначая их #(*,Д) и Л(*,Д), получаем Функция v(t9 Ji) была определена при Д Ф ц. Доопределяем ее при Д = /м как решение уравнения (9) с начальным условием и(*0, ц) = a'(/i), полученным из начального условия (7) при . По теореме 7 §7 функция v(t9JT) непрерывна по Д, включая Д = /х.

Возможно вам будут полезны данные страницы:

При Д = /х имеем х* = х = /*), /1* = ц9 подынтегральные выражения в (8) не зависят от 8. Тогда в (9) матрица Я и вектор h принимают значения Таким образом, для v(t9fi) уравнение (9) и начальное условие v(t0,n) = a'(fi) совпадают с (2), то есть v(t9fi) удовлетворяет (2). В силу непрерывности Д) существует lim v(t9 Д) = То есть в (5) существует производная дх/дц = и координаты tf. вектора v(t9 ц) удовлетво- ряют системе уравнений и начальным условиям (2). Теперь пусть ц меняется на интервале М.

(и производные д/ди от них) непрерывны по (*,/*). По теореме 7 §7 решение системы (2), то есть производные тоже непрерывны по Дифференцнруемость решения по начальным условиям (следствие теоремы 1). Рассмотрим начальную задачу Пусть при (*,s) е D все функции Д и непрерывны, и на отрезке [t<912] Э t0 решение задачи (10) существует и проходит в области D. Тогда при существуют непрерывные производные решения £, по начальным условиям удовлетворяют системе Здесь решение задачи (10). Доказательство. Пусть xk0 = /х, а при t ^ fc ®f0 не зависит от Тогда система (10) удовлетворяет условиям теоремы 1.

Тогда решение x(t, ц) имеет непрерывные по t, ц производные по ц до порядка т включительно. Доказательство производится с помощью индукции по т. Для т = 1 утверждение теоремы 2 следует из теоремы 1. Пусть утверждение верно для производных до порядка 771 — 1 ^ 1. Докажем, что оно верно и для производных порядка т. Так как а функции и. = dxjdpi (i = 1. 7i) удовлетворяют системе (2), то надо проверить, что правые части в (2) имеют непрерывные производные по щ, fi до порядка т — 1 включительно.

1 по /i. Значйт, в (2) сложная функция принадлежит , аналогично dfjd^ также . По предположению индукции, примененному к системе (2), решение ир. ип системы (2) принадлежит по р. Так как ий =, то xt(t9 fi) G .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Производная функции, заданной параметрическим способом

Формула производной

Пусть функция задана параметрическим способом:
(1)
где некоторая переменная, называемая параметром. И пусть функции и имеют производные при некотором значении переменной . Причем и функция имеет обратную функцию в некоторой окрестности точки . Тогда функция (1) имеет в точке производную , которая, в параметрическом виде, определяется по формулам:
(2)

Здесь и – производные функций и по переменной (параметру) . Их часто записывают в следующем виде:
;
.

Тогда систему (2) можно записать так:

Доказательство

По условию, функция имеет обратную функцию. Обозначим ее как
.
Тогда исходную функцию можно представить как сложную функцию:
.
Найдем ее производную, применяя правила дифференцирования сложной и обратной функций:
.

Доказательство вторым способом

Найдем производную вторым способом, исходя из определения производной функции в точке :
.
Введем обозначение:
.
Тогда и предыдущая формула принимает вид:
.

Воспользуемся тем, что функция имеет обратную функцию , в окрестности точки .
Введем обозначения:
; ;
; .
Разделим числитель и знаменатель дроби на :
.
При , . Тогда
.

Производные высших порядков

Чтобы найти производные высших порядков, надо выполнять дифференцирование несколько раз. Допустим, нам надо найти производную второго порядка от функции, заданной параметрическим способом, следующего вида:
(1)

По формуле (2) находим первую производную, которая также определяется параметрическим способом:
(2)

Обозначим первую производную, посредством переменной :
.
Тогда, чтобы найти вторую производную от функции по переменной , нужно найти первую производную от функции по переменной . Зависимость переменной от переменной также задана параметрическим способом:
(3)
Сравнивая (3) с формулами (1) и (2), находим:

Теперь выразим результат через функции и . Для этого подставим и применим формулу производной дроби:
.
Тогда
.

Отсюда получаем вторую производную функции по переменной :

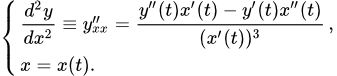
Она также задана в параметрическом виде. Заметим, что первую строку также можно записать следующим образом:
.

Продолжая процесс, можно получить производные функции от переменной третьего и более высоких порядков.

Заметим, что можно не вводить обозначение для производной . Можно записать так:
;
.

Пример 1

Найдите производную от функции, заданной параметрическим способом:

Пример 2

Найдите производную от функции, выраженной через параметр :

Раскроим скобки, применяя формулы для степенных функций и корней:
.

Находим производную . Для этого введем переменную и применим формулу производной сложной функции.

.

Находим искомую производную:
.

Пример 3

Найдите производные второго и третьего порядков от функции, заданной параметрическим способом в примере 1:

В примере 1 мы нашли производную первого порядка:

Введем обозначение . Тогда функция является производной по . Она задана параметрическим способом:

Чтобы найти вторую производную по , нам надо найти первую производную по .

Дифференцируем по .
.
Производную по мы нашли в примере 1:
.
Производная второго порядка по равна производной первого порядка по :
.

Итак, мы нашли производную второго порядка по в параметрическом виде:

Теперь находим производную третьего порядка. Введем обозначение . Тогда нам нужно найти производную первого порядка от функции , которая задана параметрическим способом:

Производная третьего порядка по равна производной первого порядка по :
.

Замечание

Можно не вводить переменные и , которые являются производными и , соответственно. Тогда можно записать так:
;
;
;
;
;
;
;
;
.

В параметрическом представлении, производная второго порядка имеет следующий вид:

Производная третьего порядка:

Автор: Олег Одинцов . Опубликовано: 22-01-2017