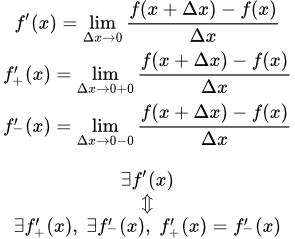Найти производную в точке если дано уравнение

Определение производной функции в точке

Определение производной

В определении (1), приращение аргумента является одной переменной, хотя ее обозначение состоит из двух букв: и . Обычно переменную принято обозначать одной буквой или буквой с одним или несколькими индексами. Но приращение в математическом анализе настолько часто встречается, что его обозначают с небольшим нарушением правил. Приращение функции также является одной переменной.

В приведенном выше определении, является независимой переменной, а – зависимой. зависит от двух переменных. Если использовать выражение , то приращение функции зависит от переменных x и . Если использовать , то зависит от x и . Но когда мы вычисляем производную в заданной точке x , то считаем, что x является постоянной. Тогда является функцией, зависящей только от одной переменной . Таким образом задача о нахождении производной в точке x сводится к задаче о вычислении предела от функции , зависящей от одной переменной при , или от функции , зависящей от одной переменной при .

В правой части (1) мы сделали замену, и перешли от переменной к переменной . Тогда . При ,
.

После того, как мы нашли производную в заданной точке, то x уже можно считать не фиксированным числом, а переменной. То есть предел (1) можно рассматривать как функцию от x .

Еще раз подчеркнем, что выражение является функцией от двух переменных: x и . А выражение , полученное после вычисления предела, зависит только от одной переменной x .

Обозначение производной

Обозначение Лагранжа

Наиболее популярным является обозначение Лагранжа. Производную функции обозначают как и саму функцию, добавляя штрих после ее характеристики: . Если функция задана алгебраическим выражением, то это выражение заключают в скобки, и ставят знак штриха справа за закрывающей скобкой: . При этом производная также является функцией от той же переменной x , что и . Правда область определения производной может не совпадать с областью определения функции, а является ее подмножеством.

Напомним, что в обозначении функции фигурируют три символа: независимая переменная, характеристика функции и зависимая переменная (см. «Определение функции»). Так, в выражении
(2) ,
x является независимой переменной, или аргументом функции; f – характеристикой функции; y – зависимой переменной, или значением функции. Обозначение зависимой переменной может совпадать или не совпадать с обозначением характеристики. Производную функции (2) обозначают так:
.

Независимую переменную производной обозначают так же, как и независимую переменную функции. В нашем случае это x .

Характеристику производной обозначают тем же символом, что и характеристику функции, добавляя штрих справа: .

Зависимую переменную производной обозначают аналогично характеристике, добавляя штрих к обозначению зависимой переменной функции. Так, для примера (2), это будет : .

Если функция зависит от нескольких переменных, например
(3) ,
но все кроме одной считают постоянными, то к характеристике производной добавляют нижний индекс, обозначающий ту переменную, по которой вычисляют производную. При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: . Здесь подразумевается, что переменные и мы считаем постоянными. Тогда в данном контексте, является функцией от одной переменной . К зависимой переменной производной также добавляют нижний индекс переменной, по которой выполняется дифференцирование:
.
Подобные производные функций от нескольких переменных называются частными производными. Детально они будут рассмотрены позже.

Нижний индекс добавляют и при вычислениях, связанных со сложными функциями. Пусть, например, функцию можно представить как сложную: , составленную из двух функций: и . При этом множества значений функций и совпадают. Поэтому их удобно обозначить одной переменной y . Тогда производную от y , выраженную через переменную x , обозначают как :
.
А производную от y , выраженную через переменную , обозначают как :
.

Обозначение производной по времени в физике

В механике и физике, производную по времени обозначают не штрихом, а точкой над зависимой переменной. Обычно время обозначают буквой t . Тогда
.

Обозначение Лейбница

В способе Лейбница, зависимую переменную обозначают в форме отношения дифференциалов:
.
Этот способ удобен, поскольку указывает, по какой переменной ведется дифференцирование. Такой способ применяется только для функций от одной переменной. Для функций от многих переменных используют обозначение частной производной: .

Иногда в форме дифференциалов обозначают характеристику производной, добавляя справа аргумент:
.
Однако этот способ скорее неудачен, и может привести к путанице.

Обозначение Коши

Также, для обозначения производной, используют обозначение Коши:
.
Но мы не будем им пользоваться.

Существование производной

Рассмотрим вопрос о существовании предела, который используется при вычислении производной, при заданном значении x :
(4) .
Здесь могут возникнуть три случая:
1) в точке x существует конечный предел (4);
2) существует бесконечный предел или ;
3) предела (4) не существует.

1) Если существует конечный предел (4), то говорят, что функция имеет производную в точке x .

2) Если в некоторой точке x существует бесконечный предел (4), то говорят, что производной в этой точке не существует. Это согласуется с определением, ⇑ в котором указано, что производной называется конечный предел. Однако при этом говорят, что функция f имеет в точке x бесконечную производную, равную или . Здесь стоит обратить внимание на различие в определении предела и производной. Возможна ситуация, когда предел (4) существует (равный бесконечности), но при этом производная не существует (хотя существует ее значение, равное бесконечности).
См. пример ⇓.

3) Если предела (4) не существует, то функция не имеет производной в точке x .

Производные справа и слева

Определение

Лемма об односторонних производных

Функция имеет в точке x производную тогда и только тогда, когда она имеет в этой точке производные справа и слева, и они равны: . При этом
.

Пусть существует производная функции в точке x . Это означает, что она определена в некоторой окрестности точки x , и существует конечный предел функции при :
.
Но тогда существуют правая и левая окрестности точки x , на которых определена. По теореме об односторонних пределах, существуют равные правый и левый пределы:
.
Отсюда следует, что в точке x существуют односторонние производные
.

Пусть теперь, в точке x , существуют равные односторонние производные:
.
Это означает, что существуют правая и левая окрестности точки x , в которой определена . И существуют односторонние равные пределы:
.
Отсюда следует, что существует двусторонняя окрестность точки x , на которой определена . И по теореме об односторонних пределах, существует двусторонний предел:
.
Это означает, что в точке x существует производная
.

Следствие

Если функция имеет в точке x не равные односторонние производные, то она не имеет производной в этой точке.

Действительно, допустим противное. Пусть функция имеет в точке x не равные односторонние производные, но при этом имеет производную в этой точке. Тогда, согласно лемме об односторонних производных, она имеет в этой точке равные производные слева и справа, что противоречит предположению.

Примеры вычисления производной, используя определение

Все примеры Здесь и далее мы приводим подробные решения примеров, в которых нужно вычислить производную функции , используя определение производной ⇑.
решение ⇓ ; ⇓ ; ⇓ .

Пример

Все примеры ⇑ Найти производную функции , используя определение производной.

Функция определена для всех x . Поэтому она определена в любой окрестности любой точки x . Используем определение (1). Считаем, что x – фиксированное число, то есть что его значение задано. Найдем приращение функции в точке x :

.
Находим отношение приращения функции к приращению ее аргумента:
.
Находим предел функции , зависящей от переменной . При этом считаем, что x является фиксированным, заданным числом:
.

Итак, мы нашли производную:
.
Поскольку вычисленный нами предел существует, и является конечным числом для всех x , то функция имеет производную для всех значений аргумента x .

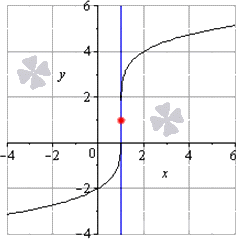
Пример бесконечной производной +∞

Все примеры ⇑ Найдем производную функции .

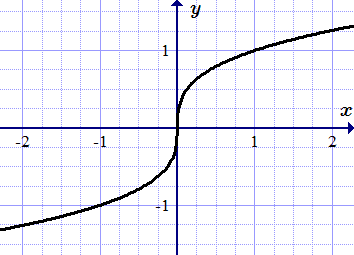
Производная функции в точке x = 0 равна плюс бесконечности.

Функция определена для всех x . Найдем отношение приращения функции к приращению ее аргумента в точке x :
.
Применим формулу . Тогда
;
(5) .
Считаем, что x является фиксированным числом. Тогда отношение является функцией от одной переменной : . При она определена для всех . При она определена для всех .

Пусть . Тогда:
.
Пусть . Подставим в (5) :
.
Поскольку , то
.

Таким образом мы нашли, что функция имеет производную для всех . При функция не имеет производной, она равна .

Пример

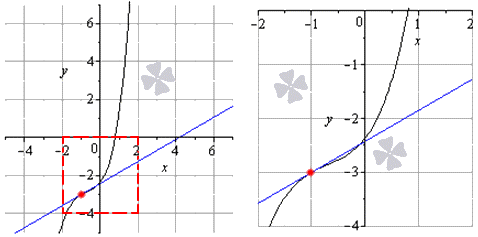
Все примеры ⇑ Найдем производную функции . Покажем, что несмотря на то, что функция определена для всех x , ее производная в точке не существует.

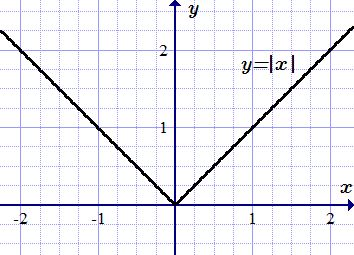
Функция y = |x| не имеет производной в точке x = 0 .

Функция определена для всех значений аргумента x . Поэтому она определена в любой окрестности произвольной точки x .

3. Рассмотрим точку . В ней
.
Найдем производную справа в точке . При этом ,
.
Теперь найдем производную слева в точке . В этом случае ,
.

Итак, мы нашли, что односторонние производные в точке существуют, но они не равны друг другу:
.
Согласно следствию леммы об односторонних производных, производной функции в точке не существует.

;
;
.
В точке производная не существует.

Использованная литература:
Г.Е. Иванов. Лекции по математическому анализу. Часть 1. Москва, МФТИ, 2018.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов . Опубликовано: 05-12-2020 Изменено: 08-11-2021

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

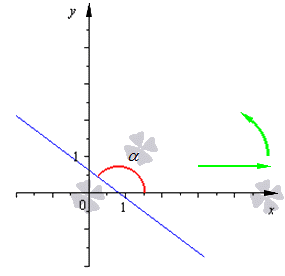
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

• Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
• Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
• Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
• Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

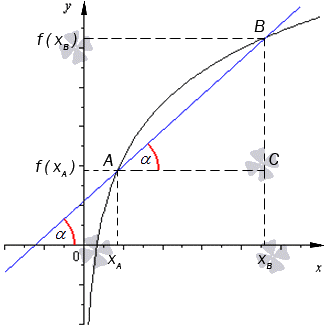
По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f ( x B ) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) — это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) — f ( x A ) x B — x A или k = f ( x A ) — f ( x B ) x A — x B , причем уравнение необходимо записать как y = f ( x B ) — f ( x A ) x B — x A · x — x A + f ( x A ) или
y = f ( x A ) — f ( x B ) x A — x B · x — x B + f ( x B ) .

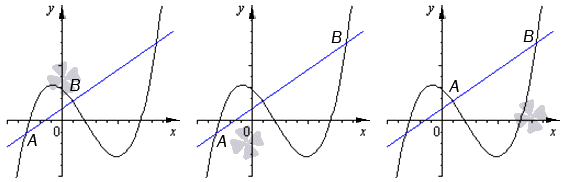
Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .

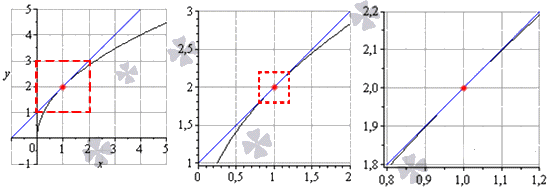
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

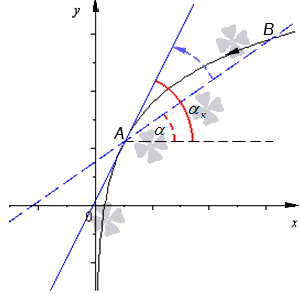
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

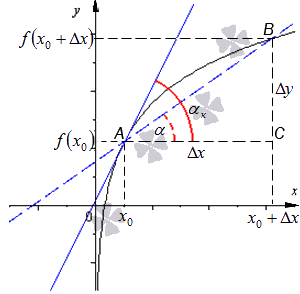
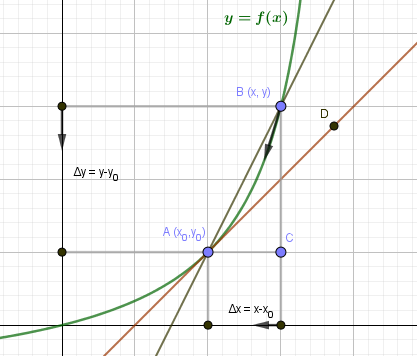
Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .

Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .

Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .

Необходимо найти производную в точке со значением — 1 . Получаем, что

y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5

Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

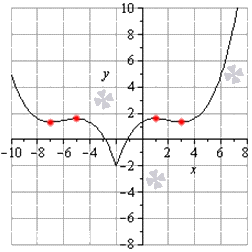
Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где

1. Касательная не существует;
2. Касательная располагается параллельно о х ;
3. Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что

y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )

Необходимо продифференцировать функцию. Имеем, что

y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )

Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3

Вычисляем значение функции в точке х = — 2 , где получаем, что

1. y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
2. Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .

Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .

— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3

Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

1. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 0

Другое уравнение имеет два действительных корня, тогда

1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3

Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

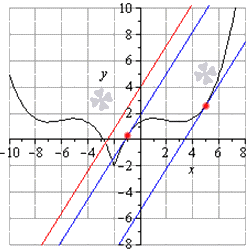
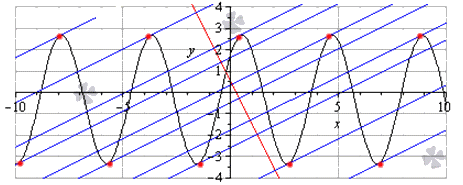
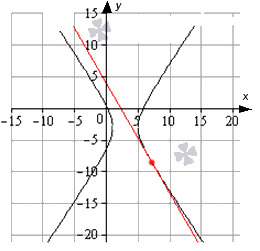
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.

y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk

3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z — множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

y 0 = 3 cos 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3

y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

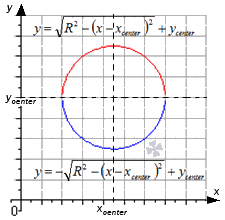
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.

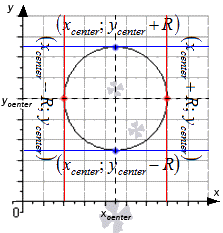
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .

Касательная к эллипсу

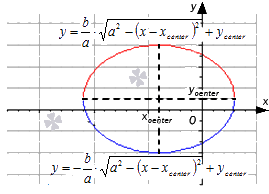
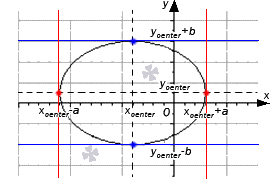
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r y = — b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

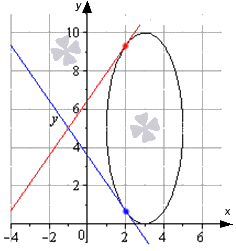
Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид

y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

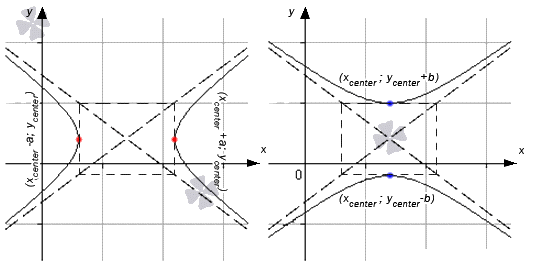
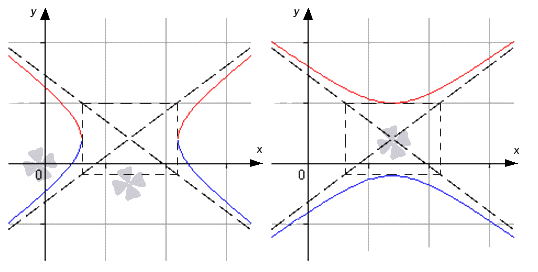
Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r или y = b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .

Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3

Ответ: уравнение касательной можно представить как

y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .

Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = — 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4

Имеем, что точки касания — 23 4 ; — 5 + 3 4 .

Ответ: уравнение касательной принимает вид

Определение, физический и геометрический смысл производной

п.1. Приращение аргумента и приращение функции

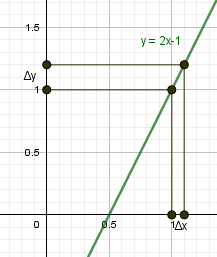	\begin 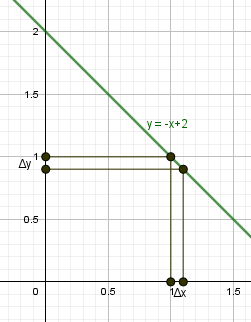y=2x-1\\ x_0=1,\ x=1,1 \end Найдем приращение аргумента и функции. \begin \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=2\cdot 1,1-1=1,2\\ f(x_0 )=f(1)=2\cdot 1-1=1\\ \triangle y=f(x)-f(x_0 )=1,2-1=0,2\gt 0 \end
	\begin y=-x+2\\ x_0=1,\ x=1,1 \end Найдем приращение аргумента и функции. \begin \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=-1,1+2=0,9\\ f(x_0 )=f(1)=-1+2=1\\ \triangle y=f(x)-f(x_0)=0,9-1=-0,1\lt 0 \end

п.2. Определение производной

Например:
Найдем производную функции \(f(x)=x^2-4\) в точке \(x_0=3\)
Значение функции в точке: \(f(x_0 )=3^2-4=5\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда: \begin f(x)=f(x_0+\triangle x)=(x_0+\triangle x)^2-4=(3+\triangle x)^2-4=9+6\triangle x+\triangle x^2-4=\\ =5+6\triangle x+\triangle x^2 \end Приращение функции: $$ \triangle y=f(x)-f(x_0)=5+6\triangle x+\triangle x^2-5=6\triangle x+\triangle x^2=\triangle x(6+\triangle x) $$ Производная: $$ f'(x_0)=\lim_<\triangle x\rightarrow 0>\frac<\triangle x><\triangle y>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(6+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(6+\triangle x)=6+0=6 $$ Ответ: 6

п.3. Физический смысл производной

Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами \(\triangle x=\) 300 км поезд преодолевает за \(\triangle t=\)4 часа. Мы легко можем найти его среднюю скорость: $$ v_=\frac<\triangle x><\triangle t>,\ \ v_=\frac<300><4>=75\ (\text<км/ч>) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.

Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:

Или, ближе к физике/химии/биологии:

п.4. Геометрический смысл производной

Пусть на плоскости задана кривая \(y=f(x)\).
Выберем на кривой две точки \(A(x_0,y_0)\) и \(B(x,y)\). Прямая AB будет секущей для кривой \(y=f(x)\). Угол наклона прямой AB определяется угловым коэффициентом: $$ k_=tg\angle A=\frac=\frac<\triangle y> <\triangle x>$$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: \(\triangle x=AC\rightarrow 0\). В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_=\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:

п.5. Алгоритм поиска значения производной в заданной точке

На входе: уравнение функции \(y=f(x)\), точка \(x_0\)
Шаг 1. Найти значение функции в заданной точке \(y_0=f(x_0)\).
Шаг 2. Задать приращение аргумента \(\triangle x=x-x_0\), найти приращение функции \(\triangle y=f(x)-f(x_0)=f(x_0+\triangle x)-f(x_0)\).
Шаг 3. Найти предел \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=f'(x_0)\)
На выходе: значение производной в точке \(x_0\)

Например:
Найдем значение производной в точке \(x_0=1\) для функции \(y=x^2-3\).
Значение функции в заданной точке: \(f(x_0)=1^2-3=-2\)
Пусть \(∆x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=((1+\triangle x)^2-3)-(-2)=\\ =1+2\triangle x+(\triangle x)^2-1=2\triangle x+(\triangle x)^2=\triangle x(2+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2+\triangle x)=2+0=2 \end Искомая производная в заданной точке: \(f'(1)=2\)
Ответ: 2

п.6. Алгоритм поиска уравнения производной

На входе: уравнение функции \(y=f(x)\)
Шаг 1. Задать приращение аргумента \(\triangle x\), найти выражение для приращения функции \(\triangle y=f(x+\triangle x)-f(x)\).
Шаг 2. Найти предел выражения \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=f'(x)\)
На выходе: уравнение производной \(y\ ‘=f'(x)\) в любой точке \(x\).

Например:
Найдем общее уравнение производной для функции \(y=x^2-3\).
Пусть \(∆x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=((x+\triangle x)^2-3)-(x^2-3)=\\ =(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2x+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2x+\triangle x)=2x+0=2x \end Ответ: уравнение производной \(y\ ‘=2x\)

п.7. Примеры

Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) \( f'(1),\ \text<если>\ f(x)=2x \)
По условию \(x_0=1\)
Значение функции в заданной точке: \(f(x_0 )=2\cdot 1=2\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=2(1+\triangle x)-2=2+2\triangle x-2=2\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<2\triangle x><\triangle x>=2 \end Искомая производная в заданной точке: \(f'(1)=2\)
б) \( f'(3),\ \text<если>\ f(x)=3x^2 \)
По условию \(x_0=3\)
Значение функции в заданной точке: \(f(x_0 )=3\cdot 3^2=27\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=3(3+\triangle x)^2-27=3(9+6\triangle x+(\triangle x)^2)-27=\\ =27+18\triangle x+3(\triangle x)^2-27=3\triangle x(6+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<3\triangle x(6+\triangle x)><\triangle x>=3\lim_<\triangle x\rightarrow 0>(6+\triangle x)=3(6+0)=18 \end Искомая производная в заданной точке: \(f'(3)=18\)

в) \( f'(-1),\ \text<если>\ f(x)=4x-1 \)
По условию \(x_0=-1\)
Значение функции в заданной точке: \(f(x_0)=4\cdot (-1)-1=-5\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=(4(-1+\triangle x)-1)-(-5)=-5+4\triangle x+5=4\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<4\triangle x><\triangle x>=4 \end Искомая производная в заданной точке: \(f'(-1)=4\)

г) \( f'(2),\ \text<если>\ f(x)=x^3 \)
По условию \(x_0=2\)
Значение функции в заданной точке: \(f(x_0)=2^3=8\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=(2+\triangle x)^3-8=\\ =2^3+3\cdot 2^2\cdot \triangle x+3\cdot 2\cdot (\triangle x)^2+(\triangle x)^3-8=\\ =12\triangle x+6(\triangle x)^2+(\triangle x)^3=\triangle x\cdot (12+6\triangle x+(\triangle x)^2 ) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x\cdot(12+6\triangle x+(\triangle x)^2)><\triangle x>=\lim_<\triangle x\rightarrow 0>(12+6\triangle x+(\triangle x)^2)=12+0+0=12 \end Искомая производная в заданной точке: \(f'(2)=12\)

Ответ: а) 2; б) 18; в) 4; г) 12

Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции \(y=f(x)\):
a) \( f(x)=C\), где C – постоянная величина
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=C-C=0 \end Отношение \(\frac<\triangle y><\triangle x>=\frac<0><\triangle x>=0\)
Предел \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>0=0\)
Производная \(y\ ‘=C’=0\)

б) \( f(x)=x\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=x+\triangle x-x=\triangle x \end Ищем предел: \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x><\triangle x>=\lim_<\triangle x\rightarrow 0>1=1\)
Производная \(x\ ‘=1\)

в) \( f(x)=x^2\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2x+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2x+\triangle x)=2x+0=2x \end Производная \((x^2)\ ‘=2x\)

г) \( f(x)=x^3\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^3-x^3=\\ =(x+\triangle x-x)((x+\triangle x)^2+x(x+\triangle x)+x^2)=\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2)><\triangle x>=\\ =\lim_<\triangle x\rightarrow 0>((x+\triangle x)^2+x(x+\triangle x)+x^2)=(x+0)^2+x(x+0)+x^2=3x^2 \end Производная \((x^3)\ ‘=3x^2\)

e) \( f(x)=kx+b\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=k(x+\triangle x)+b-kx-b=k\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x>=\lim_<\triangle x\rightarrow 0>k=k \end Производная \((kx+b)\ ‘=k\)