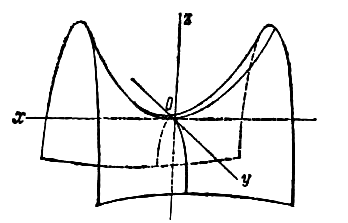
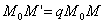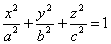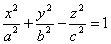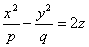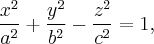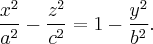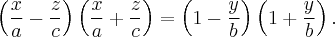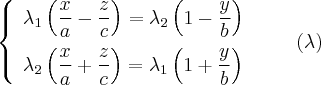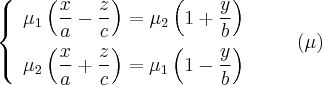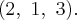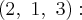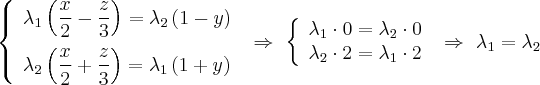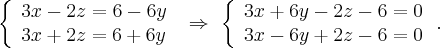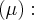Найти прямолинейные образующие поверхности задаваемой уравнением

Найти прямолинейные образующие поверхности задаваемой уравнением

Глава 46. Поверхности второго порядка

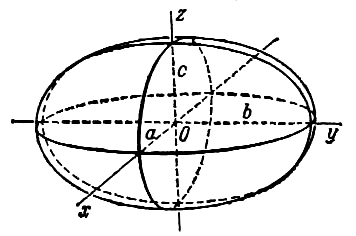
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

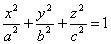
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

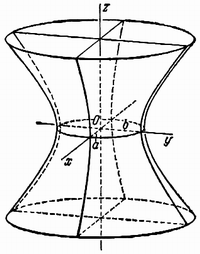
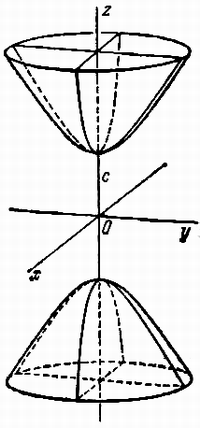
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

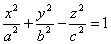
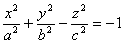
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

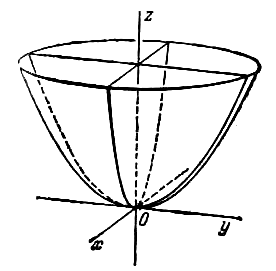
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

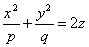
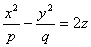
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

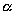
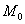
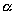
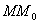
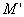
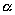
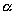
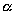
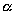
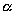
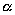
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .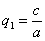

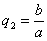
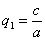
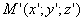
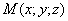
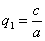
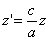
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

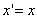
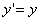
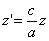
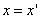
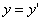
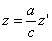
Предположим, что M(x; y; z ) — произвольная точка сферы

.

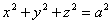
Заменим здесь x, y, z их выражениями (7); получим

,

.

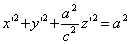
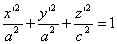
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

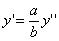
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

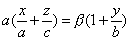
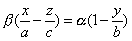
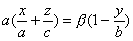
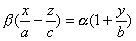
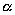
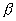
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

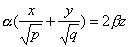
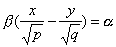
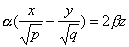
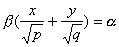
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

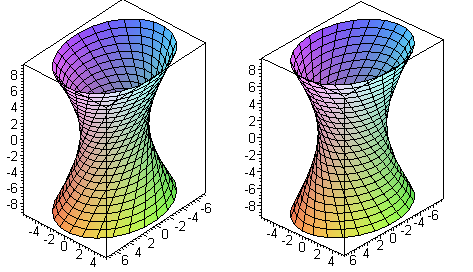
Прямолинейные образующие на поверхности однополостного гиперболоида

Уравнение однополостного гиперболоида имеет вид:

Разложим на множители:

Рассмотрим следующую систему линейных уравнений:

Каждое линейное уравнение задает в пространстве плоскость. Данные плоскости не параллельны, следовательно эта система из двух линейных уравнений задает прямую. Покажем, что эта прямая лежит на Однополостный гиперболоид. Действительно, если точка принадлежит этой прямой, то она удовлетворяет каждое из линейных уравнений системы, следовательно удовлетворяет произведения этих уравнений, то есть уравнению однополостного гиперболоида.

Это утверждение справедливо для любых 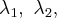которые не равны нулю одновременно. Итак, мы получили уравнение одной семьи прямолинейных образующих на Однополостный гиперболоид.

Уравнение второй семьи :

Теорема. Однополостный гиперболоид несет на себе две семьи прямолинейных образующих, имеющих следующие свойства:

· через любую точку проходит ровно одна прямая с каждой семьи ;

· любые две образующие из разных семей лежат в одной плоскости;

· любые две образующие с одной семьи является скрещивающимися;

· любые три образующие с одной семьи не параллельны одной плоскости.

Доказательство можно посмотреть в методичке.

Пример. Найти прямолинейные образующие поверхности 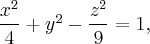которые проходят через точку

Запишем уравнение первой семьи прямолинейных образующих 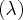и подставим координаты точки

Можем взять любые числа, удовлетворяющие этому равенства, например: 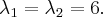Получаем уравнение прямолинейной образующей с первой семьи :

Уравнение второй семьи

Возьмем, 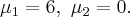получаем уравнение прямолинейной образующей с другойсемье :

Найти прямолинейные образующие поверхности задаваемой уравнением

С помощью векторов мы ввели понятие пространства и его размерности, в частности трехмерного. Рассмотрим в нем поверхности, которые «похожи» на поверхности, образованные вращением кривой второго порядка вокруг ее оси симметрии. Например, сфера может быть получена вращением окружности вокруг диаметра. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. Наряду с такими поверхностями мы встретимся и с более сложными случаями.

Пусть в пространстве задана прямоугольная декартова система координат.

Поверхность второго порядка – геометрическое место точек, декартовы прямоугольные координаты которых, удовлетворяют уравнению вида

в котором хотя бы один из коэффициентов отличен от нуля. Уравнение (2.48) называется общим уравнением поверхности второго порядка.

Уравнение (2.48) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую поверхность второго порядка. В зависимости от значений коэффициентов общего уравнения (2.48) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из канонических видов, каждому из которых соответствует определённый класс поверхностей второго порядка. Среди них выделяют пять основных классов поверхностей: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением.

Перечисленные поверхности второго порядка относятся к так называемым нераспадающимся поверхностям второго порядка. Можно говорить о случаях вырождения – распадающихся поверхностях второго порядка, к которым относятся: пары пересекающихся плоскостей, пары мнимых пересекающихся плоскостей, пары параллельных плоскостей, пары мнимых параллельных плоскостей, пары совпадающих плоскостей.

Наша цель – указать канонические уравнения для поверхностей второго порядка и показать, как выглядят эти поверхности.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется эллипсоидом (рис. 2.22) .

1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что .

2. Эллипсоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно координатных осей,

· плоскостной симметрией относительно начала координат.

3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс (см. рис. 2.22).

Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии – центром эллипсоида. Числа а, b , с называются полуосями. Если полуоси попарно различны, то эллипсоид называется трехосным.

Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.

Примечание. Сфера является частным случаем эллипсоида при а= b =с. Тогда все равные полуоси обозначают R и уравнение (2.49) после умножения на R 2 принимает вид .

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется эллиптическим параболоидом (рис. 2.23) .

1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.

2. Эллиптический параболоид обладает

· осевой симметрией относительно оси 0z ,

· плоскостной симметрией относительно координатных осей 0xz и 0yz .

3. В сечении эллиптического параболоида плоскостью, ортогональной оси 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y –парабола. (см. рис. 2.23).

Можно получить эллиптический параболоид симметричный относительно оси 0х или 0у, для чего нужно в уравнении (2.50) поменять между собой переменные х и z или у и z соответственно.

Если полуоси равны a = b , то параболоид называется параболоидом вращения и может быть получен вращением параболы вокруг ее оси симметрии. При этом в сечении параболоида вращения плоскостью, перпендикулярной оси 0z , получается окружность.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется гиперболическим параболоидом (рис . 2.24).

Свойства гиперболического параболоида.

1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Гиперболический параболоид обладает

· осевой симметрией относительно оси 0z ,

· плоскостной симметрией относительно координатных плоскостей 0xz и 0yz .

4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.

5. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется однополостным гиперболоидом (рис. 2.25) .

Свойства однополостного гиперболоида.

1. Однополостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Однополостный гиперболоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно всех координатных осей,

· плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y, – гипербола (см. рис. 2.25).

Если в уравнении (2.52) a = b , то сечения однополостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется двуполостным гиперболоидом (рис. 2.26) .

1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что | z |≥ c и неограничен сверху.

2. Двуполостный гиперболоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно всех координатных осей,

· плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , при | z |> c получается эллипс, при | z |= c – точка, а в сечении плоскостями, перпендику­лярными осям 0x и 0y , – гипербола (см. рис. 2.26).

Если в уравнении (2.53) a = b , то сечения двуполостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется двуполостным гиперболоидом вращения.

Примечание. Если уравнение поверхности в прямоугольной системе координат имеет вид: F ( x 2 + y 2 ; z )=0, то эта поверхность – поверхность вращения с осью вращения 0z. Аналогично: F ( x 2 + z 2 ; y )=0 – поверхность вращения с осью вращения 0у, F ( z 2 + y 2 ; x )=0 – с осью вращения 0х

С учетом данного примечания могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси 0х или 0у.

Цилиндрическая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и остающейся параллельной своему исходному положению. Множество прямолинейных образующих представляет собой непрерывный каркас цилиндрической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая. Неподвижная кривая, по которой скользит образующая, называется направляющей. Если направляющая линия является кривой второго порядка, то и цилиндрическая поверхность – второго порядка.

Если уравнение поверхности не содержит в явном виде какой–либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.

Достаточно нарисовать на плоскости х0у направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 0z. Для наглядности следует построить также одно–два сечения плоскостями, параллельными плоскости х0у. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Аналогично поступают, рассматривая направляющую в плоскости х0z или у0z.

Цилиндрическая поверхность является бесконечной в направлении своих образующих. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения – его основаниями. Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают:

1) эллиптические – нормальное сечение представляет собой эллипс (рис. 2.27а), каноническое уравнение

2) круговые – нормальное сечение круг, при a = b = r уравнение

3) гиперболические – нормальное сечение гипербола (рис. 2.27б), каноническое уравнение

4) параболические – нормальное сечение парабола (рис. 2.27в), каноническое уравнение

5) общего вида – нормальное сечение кривая случайного вида.

Если за основание цилиндра принимается его нормальное сечение, цилиндр называют прямым (рис. 2.27). Если за основание цилиндра принимается одно из косых сечений, цилиндр называют наклонным. Например, наклонные сечения прямого кругового цилиндра являются эллипсами. Наклонные сечения прямого эллиптического цилиндра в общем случае – эллипсы. Однако его всегда можно пересечь плоскостью, наклонной к его образующим, таким образом, что в сечении получится круг.

Конической поверхностью называется поверхность, производимая движением прямой, перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку и пересекает данную линию. Данная прямая называется образующей, линия – направляющей, а точка – вершиной конической поверхности (рис. 2.28).

Конусом называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая боковой поверхностью, – основанием конуса. Перпендикуляр, опущенный из вершины на плоскость основания, называется высотой конуса.

Конус называется прямым круговым, если его основание есть круг, а высота проходит через центр основания. Такой конус можно рассматривать как тело, происходящее от вращения прямоугольного треугольника, вокруг катета как оси. При этом гипотенуза описывает боковую поверхность, а катет – основание конуса.

В курсе геометрии общеобразовательной школы рассматривается только прямой круговой конус, который для краткости называется просто конусом.

Если вершина конуса расположена в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат, то уравнение эллиптического конуса имеет вид:

( a >0, b >0, c >0). (2.58)

При а = b конус становится круговым.

Примечание. По аналогии с коническими сечениями (аналогично теореме 2.1) существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x 2 = 0 описывается пара совпадающих плоскостей, уравнением x 2 = 1 – пара параллельных плоскостей, уравнением x 2 – y 2 = 0 – пара пересекающихся плоскостей. Уравнение x 2 + y 2 + z 2 = 0 описывает точку с координатами (0;0;0). Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии