Расстояние между прямыми в пространстве онлайн
С помощю этого онлайн калькулятора можно найти расстояние между прямыми в пространстве. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между прямыми в пространстве − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
 . . | (1) |
 , , | (2) |
Прямые (1) и (2) в пространстве могут совпадать, быть паралленьными, пересекаться, или быть скрещивающимся. Если прямые в пространстве пересекаются или совпадают, то расстояние между ними равно нулю. Мы рассмотрим два случая. Первый − прямые параллельны, и второй − прямые скрещиваются. Остальные являются частыми случаями. Если при вычислении расстояния между параллельными прямыми мы получим расстояние равным нулю, то это значит, что эти прямые совпадают. Если же расстояние между скрещивающимися прямыми равно нулю, то эти прямые пересекаются.
1. Расстояние между параллельными прямыми в пространстве
Рассмотрим два метода вычисления расстояния между прямыми.
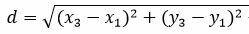  |
которое и является расстоянием между прямыми L1 и L2 (Рис.1).
 |
Пример 1. Найти расстояние между прямыми L1 и L2:
 | (3) |
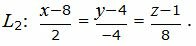 | (4) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Найдем проекцию точки M1 на прямую L2. Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.
Для того, чтобы плоскость α было перепендикулярна прямой L2, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L2, т.е. в качестве нормального вектора плоскости α можно взять направляющий вектор прямой L2. Тогда уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) имеет следующий вид:
| m2<x−x1)+p2(y−y1)+ l2(z−z1)=0 | (5) |
| 2(x−1)−4(y−2)+ 8(z−1)=0 |
После упрощения получим уравнение плоскости, проходящей через точку M1 и перпендикулярной прямой L2:
| 2x−4y+ 8z−2=0 | (6) |
Найдем точку пересечения прямой L2 и плоскости α, для этого построим параметрическое уравнение прямой L2.
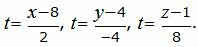 |
Выразив переменные x, y, z через параметр t, получим параметрическое уравнение прямой L2:
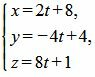 | (7) |
Чтобы найти точку пересечения прямой L2 и плоскости α, подставим значения переменных x, y, z из (7) в (6):
 |
Решив уравнение получим:
 | (8) |
Подставляя полученное значение t в (7), получим точку пересеченияпрямой L2 и плоскости α:
 |
Остается найти расстояние между точками M1 и M3:
 |
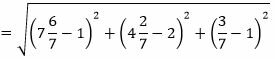  |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.2506.
Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Во первых, проверяем параллельность прямых L1 и L2. Если направляющие векторы прямых L1 и L2 коллинеарны, т.е. если существует такое число λ, что выполнено равенство q1=λq2, то прямые L1 и L2 параллельны.
Данный метод вычисления расстояния между параллельными векторами основана на понятии векторного произведения векторов. Известно, что норма векторного произведения векторов 
 |
Вычислим координаты вектора 
 |
Вычислим векторное произведение векторов 
 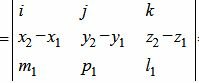 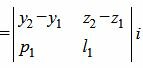  |
Вычисляя определители второго порядка находим координаты вектора c:
Далее находим площадь параллелограмма:
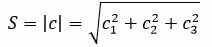 . . |
Расстояние между прямыми L1 и L2 равно:
 , , |
 , , |
Пример 2. Решим пример 1 методом 2. Найти расстояние между прямыми
 | (25) |
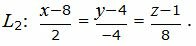 | (26) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Векторы q1 и q2 коллинеарны. Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.
Построим вектор 
Вычислим векторное произведение векторов 

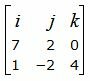 |
Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов 
   |
Таким образом, результатом векторного произведения векторов 
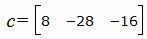 |
Поскольку векторное произведение векторов 
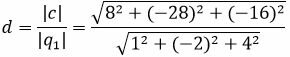  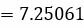 |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.25061.
2. Расстояние между скрещивающимися прямыми в пространстве
Пусть задана декартова прямоугольная симтема координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 (уравнения (1) и (2)).
Пусть прямые L1 и L2 не параллельны (паралельные прямые мы расстотрели в предыдущем параграфе). Чтобы найти расстояние между прямыми L1 и L2 нужно построить параллельные плоскости α1 и α2 так, чтобы прямая L1 лежал на плоскости α1 а прямая L2 − на плоскости α2. Тогда расстояние между прямыми L1 и L2 равно расстоянию между плоскостями L1 и L2 (Рис. 3).
 |
Поскольку плоскость α1, проходит через прямую L1, то он проходит также через M1(x1, y1, z1). Следовательно справедливо следующее равенство:
| A1x1+B1y1+C1z1+D1=0. | (27) |
где n1=<A1, B1, C1> − нормальный вектор плоскости α1. Для того, чтобы плоскость α1 проходила через прямую L1, нормальный вектор n1 должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
| A1m1+B1p1+C1l1=0. | (28) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (29) |
Решая систему линейных уравнений (27)−(29), с тремя уравнениями и четыремя неизвестными A1, B1, C1, D1, и подставляя в уравнение
| A1x+B1y+C1z+D1=0. | (30) |
получим уравнение плоскости α1. (Как построить уравнение плоскости, проходящей через прямую, параллельно другой прямой подробно изложено здесь).
Аналогичным образом находим уравнение плоскости α2:
| A2x+B2y+C2z+D2=0. | (31) |
Плоскости α1 и α2 параллельны, следовательно полученные нормальные векторыn1=<A1, B1, C1> и n2=<A2, B2, C2> этих плоскостей коллинеарны. Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).
Тогда расстояние между параллельными плоскостями вычисляется формулой:
 . . |
Полученное расстояние между плоскостями α1 и α2 является также расстоянием между прямыми L1 и L2.
Пример 3. Найти расстояние между прямыми
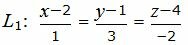 | (32) |
 | (33) |
Построим плоскость α1, проходящую через прямую L1, параллельно прямой L2.
Поскольку плоскость α1 проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(2, 1, 4) и нормальный вектор n1=<m1, p1, l1> плоскости α1 перпендикулярна направляющему вектору q1 прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
| A1x1+B1y1+C1z1+D1=0. | (34) |
а условие параллельности прямой L1 и искомой плоскости α1 представляется следующим условием:
| A1m1+B1p1+C1l1=0. | (35) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (36) |
| A1·2+B1·1+C1·4+D1=0. | (37) |
| A1·1+B1·3+C1·(−2)=0. | (38) |
| A1·2+B1·(−3)+C1·7=0. | (39) |
Представим эти уравнения в матричном виде:
 | (40) |
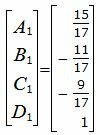 | (41) |
Искомая плоскость может быть представлена формулой:
| A1x+B1y+C1z+D1=0. | (42) |
 |
Упростим уравнение, умножив на число 17.
 | (43) |
Построим плоскость α2, проходящую через прямую L2, параллельно прямой L1.
Поскольку плоскость α2 проходит через прямую L2 , то она проходит также через точку M2(x2, y2, z2)=M2(6, −1, 2) и нормальный вектор n2=<m2, p2, l2> плоскости α2 перпендикулярна направляющему вектору q2 прямой L2. Тогда уравнение плоскости должна удовлетворять условию:
| A2x2+B2y2+C2z2+D2=0. | (44) |
а условие параллельности прямой L2 и искомой плоскости α2 представляется следующим условием:
| A2m2+B2p2+C2l2=0. | (45) |
Так как плоскость α2 должна быть параллельной прямой L1, то должна выполнятся условие:
| A2m1+B2p1+C2l1=0. | (46) |
| A1·6+B1·(−1)+C1·2+D1=0. | (47) |
| A1·2+B1·(−3)+C1·7=0. | (48) |
| A1·1+B1·3+C1·(−2)=0. | (49) |
Представим эти уравнения в матричном виде:
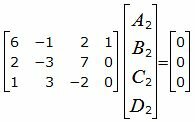 | (50) |
 | (51) |
Искомая плоскость может быть представлена формулой:
| A2x+B2y+C2z+D2=0. | (52) |
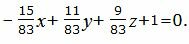 |
Упростим уравнение, умножив на число −83.
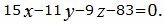 | (53) |
Расстояние между построенными плоскостями (43) и (53) будет расстоянием между прямыми (1) и (2).
Запишем формулы уравнений плоскостей α1 и α2 :
| A1x+B1y+C1z+D1=0. |
| A2x+B2y+C2z+D2=0. |
Поскольку нормальные векторы плоскостей α1 и α2 совпадают, то можно найти расстояние между плоскостями α1 и α2, используя следующую формулу:
 | (54) |
 |
Упростим и решим:
 |
Расстояние между прямыми равно: d=4.839339
Расстояние между 2 прямыми в пространстве
Вы будете перенаправлены на Автор24
Очень часто на практике необходимо найти расстояние между точкой и некой прямой линией или между двумя прямыми линиями в пространстве, например, иногда определять расстояние между двумя линиями приходится и в реальной жизни. Хорошая иллюстрация такого примера — это знак, который вешают на мосты для грузовиков, указывающий максимальную высоту грузовика, которая может проехать под данным мостом.
Расстояние от верхней грани грузовика и нижней грани в данном случае определяют как расстояние между двумя прямыми.
Расстояние между 2 прямыми в пространстве — это отрезок, соединяющий две прямые линии по наикратчайшему расстоянию между ними, то есть перпендикулярный к обеим прямым.
Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной заданной прямой и плоскостью, в которой лежит вторая прямая.
Чтобы было чуть проще понять, что это такое, давайте повторим определение скрещивающихся прямых:
Скрещивающиеся прямые — это две прямые, которые не лежат в одной плоскости и не имеют каких-либо совместных друг для друга точек.
Соответственно, для того чтобы найти расстояние между скрещивающимися прямыми в пространстве, необходимо от одной из прямых опустить перпендикуляр на плоскость, в которой лежит другая прямая.
Расстояние же между двумя параллельными прямыми в пространстве является одинаковым на протяжении всей длины параллельных прямых, то есть перпендикуляр, опущенный из одной параллельной прямой на другую, всегда будет одной и той же длины вне зависимости от того, из какой именно точки его опустили.
Метод координат для определения расстояния между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми в пространстве можно найти используя метод координат, для этого необходимо:
Готовые работы на аналогичную тему
- Найти координаты точек $M_1$ и $M_2$, лежащих на прямых $a$ и $b$ соответственно.
- Вычислить икс, игрек и зет направляющих векторов для прямых $a$ и $b$.
- С помощью векторного произведения векторов $\overline$ и $\overline$ нужно найти вектор-нормаль для плоскости, в которой лежит прямая $b$. Затем необходимо записать общее уравнение плоскости: $A (x – x_0) + B(y – y_0) + C(z – z_0) = 0$, и от него перейти к нормированному виду уравнения плоскости следующего вида: $ x \cdot cos α + y \cdot cos β + z \cdot cos <γ>– p = 0$, где $cos α, cos β$ и $cos γ$ — координаты единичного нормального вектора плоскости, а $p$ — свободный член, это число равно расстоянию от точки начала координат до плоскости.
- Для вычисления расстояния от точки $M$ до искомой плоскости, нужно воспользоваться следующим уравнением: $M_1H_1 = |x_1 \cdot cos α + y_1 \cdot cos β + z_1 \cdot cos <γ>– p|$, где $x_1, y_1, z_1$ – координаты точки $M_1$, лежащей на прямой $a$, а $H_1$ — точка, лежащая на искомой плоскости.
Найти расстояние между двумя скрещивающимися прямыми, заданными уравнениями: $d_1$: $\frac
Рисунок 1. Расстояние между двумя скрещивающимися прямыми в пространстве
Для этого воспользуемся следующей формулой:
Сначала найдём смешанное произведение векторов. Для этого найдём точки, лежащие на данных прямых, и их направляющие вектора:
$d_1$: $\frac
$d_2$: $\begin
а её направляющий вектор — $\overline
Теперь найдём вектор $\overline
Найдём смешанное произведение векторов:
$\overline
Теперь найдём векторное произведение векторов:
$[|\overline
$[|\overline
Длина этого векторного произведения составит:
Соответственно, длина между скрещивающимися прямыми составит:
Даны две параллельные несовпадающие прямые $g$ и $m$, ниже приведены уравнения для них. Определить расстояние между ними.
Расстояние в этом случае для них вычисляется по следующей формуле:
$\overline
Радиус-вектор для первой прямой будет $r_1=\<1; -1; -3\>$, а направляющий вектор $s_1 = \<4; 6; 8\>$.
Радиус-вектор для второй прямой будет $r_2=\<-1; 1; 3\>$, а направляющий вектор $s_2 = \<2; 3; 4\>$.
Найдём векторную разность радиус-векторов:
Теперь найдём её произведение с направляющим вектором для первой прямой:
$[\overline
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 09 01 2022
Взаимное расположение прямых в пространстве
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями
где — точки, принадлежащие прямым и соответственно, a — направляющие векторы (рис.4.34). Обозначим через вектор, соединяющий заданные точки.
Перечисленным выше случаям взаимного расположения прямых и соответствуют следующие признаки:
– прямые и скрещивающиеся векторы не компланарны;
– прямые и пересекаются векторы компланарны, а векторы не коллинеарны;
– прямые и параллельные векторы коллинеарны, а векторы не коллинеарны;
– прямые и совпадают векторы коллинеарны.
Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:
Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности. Поэтому:
– прямые и скрещивающиеся определитель отличен от нуля;
– прямые и пересекаются определитель равен нулю, а вторая и третья его строки не пропорциональны, т.е.
– прямые и параллельные вторая и третья строки определителя пропорциональны, т.е. а первые две строки не пропорциональны, т.е.
– прямые и совпадают все строки определителя пропорциональны, т.е.
Расстояние между параллельными прямыми
Найдем расстояние между параллельными прямыми, заданными каноническими уравнениями (рис.4.35)
где — произвольные точки на прямых и соответственно, а координаты направляющих векторов прямых пропорциональны:
Искомое расстояние равно высоте параллелограмма, построенного на векторах и , и может быть найдено по формуле (4.35).
Расстояние между скрещивающимися прямыми
Напомним, что расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра, т.е. кратчайшее расстояние между точками этих прямых.
Найдем расстояние между скрещивающимися прямыми, заданными каноническими уравнениями
где — произвольные точки на прямых и соответственно.
Искомое расстояние равно высоте параллелепипеда, построенного на векторах (рис.4.36), т.е.
— смешанное и векторное произведения векторов. Как показано выше, прямые и скрещивающиеся тогда и только тогда, когда векторы некомпланарные, т.е.
Отсюда следует, что вторая и третья строки не пропорциональны. Поэтому векторы неколлинеарные, т.е. и знаменатель в правой части (4.38) отличен от нуля.
Угол между прямыми
Угол между прямыми определяется как угол между их направляющими векторами. Поэтому величина острого угла между прямыми
вычисляется по формуле
Пример 4.16. Найти расстояние между прямой, проходящей через точки , и осью абсцисс. Найти величину острого угла между этими прямыми.
Решение. Каноническое уравнение оси абсцисс имеет вид так как ось проходит через точку а — ее направляющий вектор. Каноническое уравнение прямой получено в примере 4.15,»а»:
Полагая по формуле (4.38) получаем:
Острый угол находим по формуле (4.39):
Взаимное расположение прямой и плоскости
Возможны три случая взаимного расположения прямой и плоскости:
– прямая и плоскость пересекаются, т.е. имеют одну общую точку;
– прямая и плоскость параллельны, т.е. не имеют общих точек;
– прямая лежит в плоскости, т.е. все точки прямой принадлежат плоскости.
Получим признаки для всех этих случаев. Пусть прямая и плоскость заданы уравнениями:
т.е. прямая проходит через точку коллинеарно вектору а плоскость перпендикулярна вектору
Перечисленным выше случаям взаимного расположения прямой и плоскости соответствуют следующие признаки:
– прямая и плоскость пересекаются векторы и не ортогональны (рис.4.37,а);
– прямая и плоскость параллельны векторы и ортогональны, а точка не принадлежит плоскости (рис.4.37,б);
– прямая лежит в плоскости векторы и ортогональны, а точка принадлежит плоскости (рис.4.37,в).
Учитывая свойство скалярного произведения векторов получаем:
– прямая и плоскость пересекаются ;
– прямая и плоскость параллельны
– прямая лежит в плоскости
Угол между прямой и плоскостью
Угол между прямой и плоскостью определяется как угол между прямой и ее ортогональной проекцией на плоскость (рис.4.38). Из двух смежных углов и , как правило, выбирают меньший. Если прямая перпендикулярна плоскости (ее ортогональная проекция на плоскость является точкой), то угол считается равным . Если обозначить и углы, образованные наклонной с перпендикуляром к плоскости, то
Поскольку угол (или ) равен углу между направляющим вектором прямой и нормалью к плоскости , то . Записывая скалярное произведение через координаты множителей, получаем формулу вычисления угла между прямой и плоскостью:
Отсюда, например, следует полученное ранее необходимое условие параллельности прямой и плоскости.
http://spravochnick.ru/geometriya/rasstoyanie_mezhdu_2_pryamymi_v_prostranstve/
http://mathhelpplanet.com/static.php?p=vzaimnoe-raspolozhenie-pryamyh-v-prostranstve