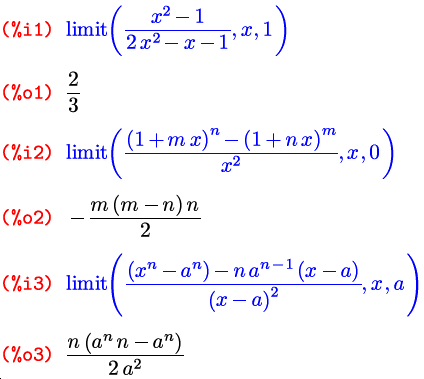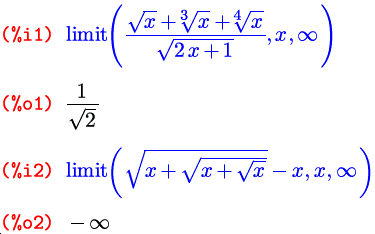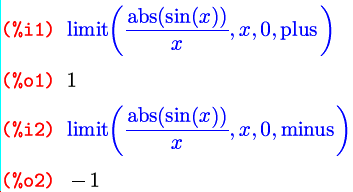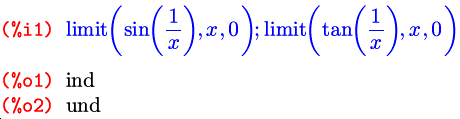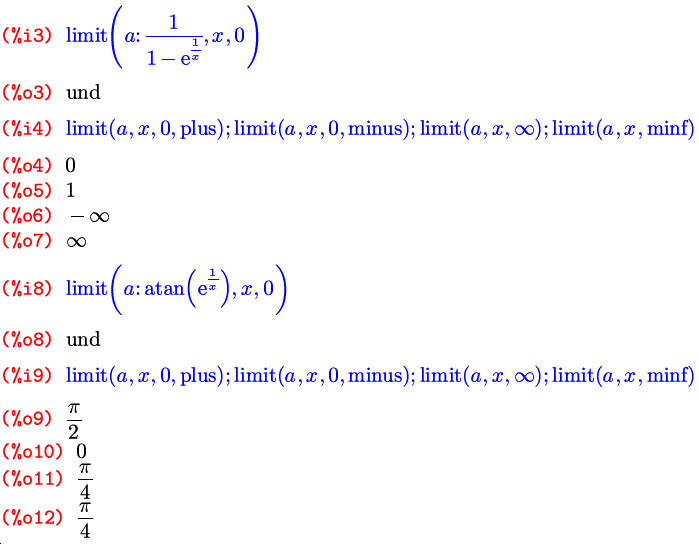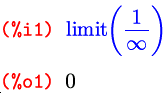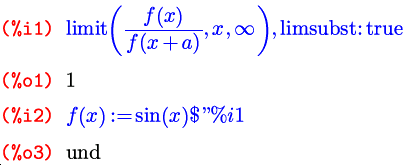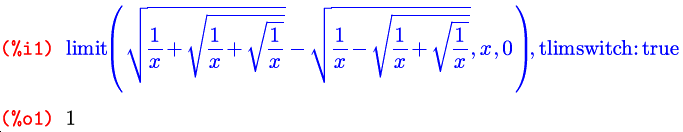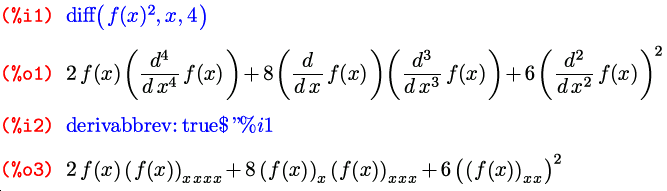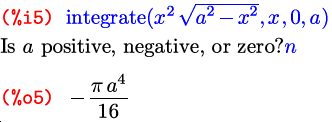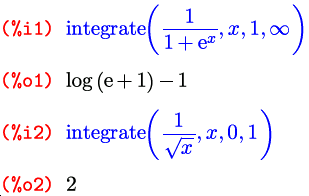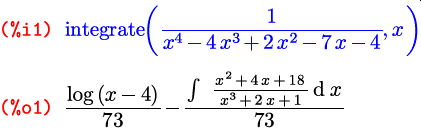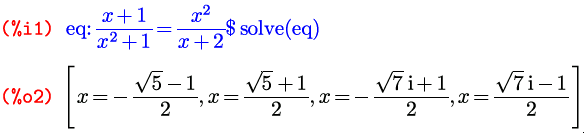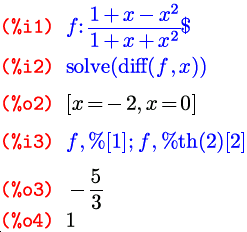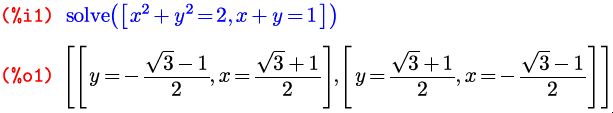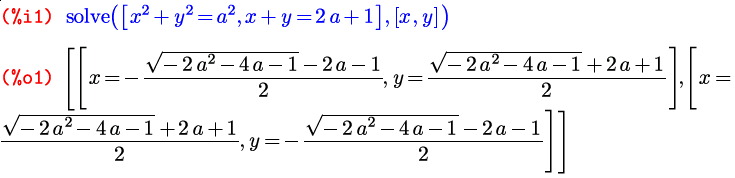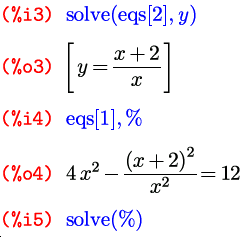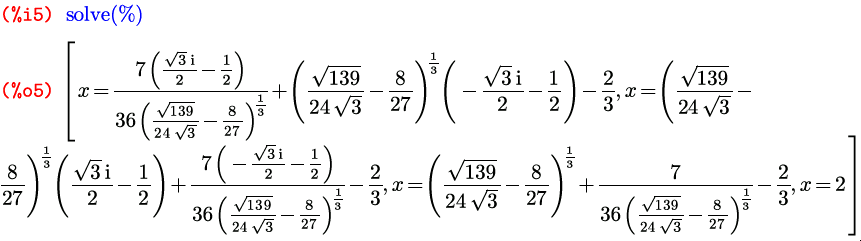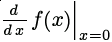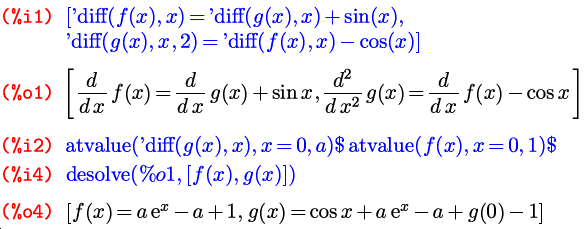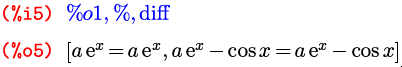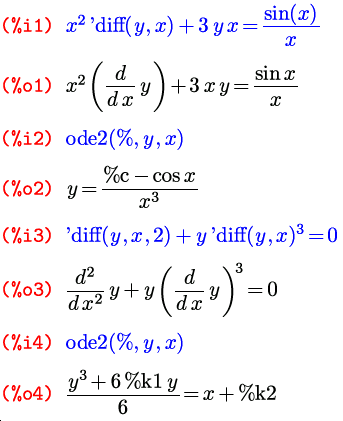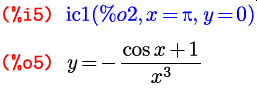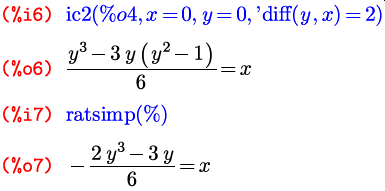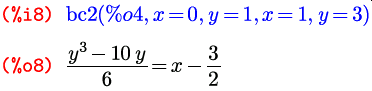Найти решение дифференциального уравнения в maxima

Дифференциальное уровнение в системе Maxima

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Кафедра информатики и вычислительной техники

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ В СИСТЕМЕ MAXIMA

Автор реферата: Д. С. Тарасов, студент 4 курса группы МДФ-113 очной формы обучения _______________________________________

Содержание

В рамках проекта создания искусственного интеллекта в 1967 году в Массачусетском технологическом институте была инициирована разработка первой системы компьютерной алгебры Macsyma. Программа в течение многих лет использовалась и развивалась в университетах Северной Америки, где появилось множество вариантов системы. Maxima является одним из таких вариантов, созданным профессором Вильямом Шелтером (William Schelter) в 1982 году. В 1998 году он получил официальное разрешение Министерства энергетики США на выпуск Maxima под лицензией GPL. А начиная с 2001 года Maxima развивается как свободный международный проект, базирующийся на SourceForge [2].

В настоящее время Maxima — это система компьютерной математики, которая предназначена для выполнения математических расчетов (как в символьном, так и в численном виде) таких как:

– графическая визуализация вычислений;

– решение уравнений и их систем;

– решение обыкновенных дифференциальных уравнений и их систем;

– решение задач линейной алгебры;

– решение задач дифференциального и интегрального исчисления;

– решение задач теории чисел и комбинаторных уравнений и др.

В системе имеется большое количество встроенных команд и функций, а также возможность создавать новые функции пользователя. Система имеет свой собственный язык. Она также имеет встроенный язык программирования высокого уровня, что говорит о возможности решения новых задач и возможности создания отдельных модулей и подключения их к системе для решения определенного круга задач.

Интерфейс основного окна Maxima

После запуска системы Maxima с графическим интерфейсом wxMaximа появляется рабочее окно программы (Рис. 1).

Рис. 1. Вид рабочего окна системы Maxima

Структура окна, как видно из рисунка, имеет стандартный вид:

– строка заголовка, в которой располагается название программы и информация о том, сохранен ли рабочий документ (если документ сохранен, то прописывается его имя);

– панель меню программы – доступ к основным функциям и настройкам программы. В ней находятся функции для решения большого количества типовых математических задач, разделенные по группам: уравнения, алгебра, анализ, упростить, графики, численные вычисления. Заметим, что ввод команд через диалоговые окна упрощает работу с программой для начинающих пользователей;

– панель инструментов — на ней находятся кнопки для создания нового документа, быстрого сохранения документа, вызова окна справки, создания ячеек ввода, прерывания вычислений, кнопки для работы с буфером обмена и др.;

– рабочая область — непосредственно сам документ, в котором формируются ячейки ввода и выводятся результаты выполненных команд;

– панель с кнопками — набор кнопок для быстрого вызова некоторых команд: упростить, решить уравнение или систему, построить график и др.;

В системе Maxima команда — это любая комбинация математических выражений и встроенных функций. Каждая команда завершается символом «;», причем в случае его отсутствия система сама добавит этот символ.

После того, как система загрузилась, можно приступать к вычислениям. Для этого следует добавить так называемую ячейку ввода, в которую вводится команда системе выполнить какое-либо действие.

Систему можно использовать в качестве мощного калькулятора для нахождения значений числовых выражений. Например, для того, чтобы найти значение произведения 120 и 1243, надо:

– на панели инструментов нажать кнопку Insert input cell (или нажать на клавиатуре клавишу Enter). В результате в рабочей области будет сформирована ячейка ввода.

– далее с клавиатуры вводим команду: 120*1243 и нажимаем комбинацию клавиш Ctrl+Enter. Выполнение вычислений в системе Maxima

Таким образом, в документе были сформированы две строки: (%i1) — ячейка ввода и для нее (%о1) — ячейка вывода. Каждая ячейка имеет свою метку — заключенное в скобки имя ячейки. Ячейки, в которых размещаются входные данные (формулы, команды, выражения) называют ячейками ввода. Они обозначаются %iChislo, где Chislo — номер ячейки ввода (i — сокращенно от английского словаinput — ввод). Ячейки, в которых размещаются выходные данные (списки значений, выражения) называют ячейками вывода. Они обозначаются %oChislo, где Chislo — номер ячейки вывода (о

— сокращенно от английского слова output — вывод).

Почему же имена ячеек начинаются с символа %? Разработчики системы Maxima посчитали удобным начинать имена всех встроенных служебных имен: констант, переменных, зарезервированных слов, с этого символа. Сделано это для того, чтобы избежать возможных накладок с пользовательскими именами.

В системе Maxima предусмотрена возможность ввода сразу нескольких команд в одной строке. Для этого одна команда от другой отделяется символом «;». При этом формируется одна строка ввода и столько строк вывода, сколько команд было задано.

Для обозначения конца ввода команды можно вместо точки с запятой использовать знак $. Это бывает удобно в том случае, если вывод результата вычисления на экран не нужен; тогда его можно «заглушить». Заглушенный результат при этом все равно будет вычисляться.

Имена функций и переменных в системе Maxima чувствительны к регистру, то есть прописные и строчные буквы в них различаются.

Задание команды в ячейке ввода и формирование ячейки вывода при нажатии комбинации клавиш Ctrl+Enter, называют отдельной сессией работы с системой Maxima.

Рассмотрим синтаксис базовых функций системы Maxima.

Операции математического анализа

Для нахождения сумм предназначена функция sum. Синтаксис функции:

Sum(выражение, переменная, нижняя граница изменения переменной, верхняя граница изменения переменной)

Если присвоить последнему аргументу значение системной переменной положительной бесконечности «inf», то это станет признаком отсутствия верхней границы и будет рассчитываться бесконечная сумма. Так же бесконечная сумма будет рассчитываться, если присвоить аргументу «нижний предел изменения переменной» значения системной переменной отрицательной бесконечности «minf». Эти же значения используется и в других функциях математического анализа.

Для нахождения конечных и бесконечных произведений используется функция product. Она имеет такие же аргументы, что и в функции sum.

Для нахождения пределов используется функция limit.

limit(выражение, переменная, точка разрыва)

Если аргументу «точка разрыва» присвоить значение «inf», то это будет признаком отсутствия границы.

Для вычисления односторонних пределов используется дополнительный аргумент, который имеет значение plus для вычисления пределов справа и minus — слева.

Например, выполним исследование непрерывности функции arctg(1/(x — 4)). Эта функция неопределенна в точке x = 4. Вычислим пределы справа и слева:

Как видим, точка x = 4 является точкой разрыва первого рода для данной функции, поскольку существуют границы слева и справа, которые равняются соответственно -PI/2 и PI/2.

Для нахождения дифференциалов используется функция diff. Синтаксис функции:

diff(выражение, переменная1, порядок производной для переменной1 [,переменная2, порядок производной для переменной2,…])

где выражение — это функция, которая дифференцируется, второй аргумент является переменной, по которой нужно брать производную, третий (необязательный) — порядок производной (по умолчанию — первый порядок).

Вообще обязательным для функции diff является только первый аргумент. В таком случае функция возвращает дифференциал выражения. Дифференциал соответствующей переменной обозначается через del(имя переменной):

Как видим из синтаксиса функции, пользователь имеет возможность определить одновременно несколько переменных дифференцирования и задать порядок для каждой из них:

Если использовать параметрическую функцию, то форма записи функции изменяется: после имени функции записываются символы «:=», а обращение к функции осуществляется через ее имя с параметром:

Производная может быть вычислена в заданной точке. Это осуществляется так:

Функция diff используется также и для обозначения производных в дифференциальных уравнениях, о чем идет речь ниже.

Для нахождения интегралов в системе используется функция integrate. Для нахождения неопределенного интеграла в функции используются два аргумента: имя функции и переменная, по которой происходит интегрирование. Например:

В случае неоднозначного ответа Maxima может задать дополнительный вопрос:

Ответ должен содержать текст из вопроса. В данном случае, если значение переменной y больше «0», это будет «positive» (положительное), а иначе — «negative» отрицательное). При этом допускается ввод только первой буквы слова.

Для нахождения определенного интеграла в функции следует указать дополнительные аргументы: пределы интеграла:

Maxima допускает задания и бесконечных пределов интегрирования. Для этого для третьего и четвертого аргументов функции используются значения «-inf» и «inf»:

Для нахождения приближенного значения интеграла в численном виде, как отмечалось ранее, следует выделить результат в ячейке вывода, вызывать на ней контекстное меню и выбрать из него пункт «To Float» (преобразовать в число с плавающей точкой).

Способна система вычислять и кратные интегралы. Для этого функции integrate вкладываются одна в другую. Ниже приводятся примеры вычисления двойного неопределенного интеграла и двойного определенного интеграла :

Решения дифференциальных уравнений

По своим возможностями в части решения дифференциальных уравнений Maxima ощутимо уступает, например, Maple. Но Maxima все же позволяет решать обычные дифференциальные уравнения первого и второго порядков, а также их системы. Для этого — в зависимости от цели — используют две функции. Для общего решения обычных дифференциальных уравнений используется функция ode2, а для нахождения решений уравнений или систем уравнений по начальным условиям — функция desolve.

Функция ode2 имеет такой синтаксис:

ode2(уравнение, зависимая переменная, независимая переменная);

Для обозначения производных в дифференциальных уравнениях используется функция diff. Но в этом случае с целью отображения зависимости функции от ее аргумента она записывается в виде ‘diff(f(x), x), а сама функция — f(x).

Пример. Найти общее решение обычного дифференциального уравнения первого порядка y’ — ax = 0.

Если значение правой части уравнения равняется нулю, то ее вообще можно опускать. Естественно, правая часть уравнения может содержать выражение.

Как видим, во время решения дифференциальных уравнений Maxima использует постоянную интегрирования %c, которая с точки зрения математики является произвольной константой, определяемой из дополнительных условий.

Осуществить решение обычного дифференциального уравнения можно и другим, более простым для пользователя, способом. Для этого следует выполнить команду Уравнения > Solve ODE (Решить обычное дифференциальное уравнение) и в окне «Решить ОДУ» ввести аргументы функции ode2.

Maxima позволяет решать дифференциальные уравнения второго порядка. Для этого также применяют функцию ode2. Для обозначения производных в дифференциальных уравнениях используется функция diff, в которой добавляют еще один аргумент — порядок уравнения: ‘diff(f(x), x, 2). Например решение обычного дифференциального уравнения второго порядка a·y» + b·y’ = 0 будет иметь вид:

Совместно с функцией ode2 можно использовать три функции, применение которых позволяет найти решение при определенных ограничениях на основании общего решения дифференциальных уравнений, полученного функцией ode2:

ic1(результат работы функции ode2, начальное значение независимой переменной в виде x = x ₀ , значение функции в точке x ₀ в виде y = y ₀ ). Предназначена для решения дифференциального уравнения первого порядка с начальными условиями.

ic2(результат работы функции ode2, начальное значение независимой переменной в виде x = x ₀ , значение функции в точке x ₀ в виде y = y ₀ , начальное значение для первой производной зависимой переменной относительно независимой переменной в виде (y,x) = dy ₀ ). Предназначена для решения дифференциального уравнения второго порядка с начальными условиями

bc2(результат работы функции ode2, начальное значение независимой переменной в виде x = x ₀ , значение функции в точке x ₀ в виде y = y ₀ , конечное значение независимой переменной в виде x = x _n , значение функции в точке x _n в виде y = y _n ). Предназначена для решения краевой задачи для дифференциального уравнения второго порядка.

Подробно с синтаксисом этих функций можно ознакомиться в документации к системе.

Выполним решение задачи Коши для уравнения первого порядка y’ — ax = 0 с начальным условием y(п) = 1.

Приведем пример решения краевой задачи для дифференциального уравнения второго порядка y»+y=x с начальными условиями y(o) = 0; y(4)=1.

Следует иметь в виду, что достаточно часто система не может решить дифференциальные уравнения. Например при попытке найти общее решение обычного дифференциального уравнения первого порядка получаем:

В таких случаях Maxima или выдает сообщение об ошибке (как в данном примере) или просто возвращает значение «false».

Другой вариант решения обычных дифференциальных уравнений первого и второго порядков предназначен для поиска решений с начальным условиями. Он реализуется с помощью функции desolve.

desolve(дифференциальное уравнение, переменная);

Если осуществляется решение системы дифференциальных уравнений или есть несколько переменных, то уравнение и/или переменные подаются в виде списка:

desolve([список уравнений], [переменная1, переменная2. ]);

Так же как и для предыдущего варианта, для обозначения производных в дифференциальных уравнениях используется функция diff, которая имеет вид ‘diff(f(x), x).

Начальные значения для переменной предоставляются функцией atvalue. Эта функция имеет такой синтаксис:

atvalue(функция, переменная = точка, значение в точке);

В данном случае предусматривается, что значения функций и (или) их производных задаются для нуля, потому синтаксис функции atvalue имеет вид:

atvalue(функция, переменная = 0, значение в точке «0»);

Пример. Найти решение дифференциального уравнения первого порядка y’=sin(x) с начальным условием.

Заметим, что и при отсутствии начального условия функция также сработает и выдаст результат:

Это позволяет осуществить проверку решения для конкретного начального значения. Действительно, подставляя в полученный результат значение y(0) = 4, как раз и получаем y(x) = 5 — cos(x).

Функция desolve дает возможность решать системы дифференциальных уравнений с начальными условиями.

Приведем пример решения системы дифференциальных уравнений с начальными условиями y(0) = 0; z(0) = 1.

Тихон Тарнавский. Maxima. Алгебра и начала анализа

Из встроенного функционала Maxima в первую очередь стоит обратить внимание на несколько групп функций: работу с пределами, дифференцирование, интегрирование, поиск решений уравнений — как «просто», так и дифференциальных.

«Предельничаем»…

Собственно полноценных функций для нахождения предела существует в Maxima аж одна. Но зато какая! Она может принимать три различных варианта списка аргументов, и кроме того, на ее действие влияют еще и три флага. Но давайте по порядку. Зовут эту функции вполне соответственно ее действию: limit ; и в самом стандартном варианте ее вызов выглядит как limit(выражение, переменная, точка) , то есть то, что в математической записи выглядит как lim _{x → a} f ( x ), в контексте Maxima запишется как limit(f(x), x, a) :

Maxima может искать пределы не только в конечных точках, но и на бесконечности. Среди стандартных обозначений программы существуют универсальные названия для разных бесконечностей: плюс-бесконечность записывается через inf (от слова infinity, как нетрудно догадаться), минус-бесконечность — через minf (от minus infinity); для комплексных чисел бесконечность, как известно, одна, и она (комплексная бесконечность) обозначается полным словом infinity . При работе с пределами все три обозначения могут как использоваться при вводе, так и возникать в виде найденного значения предела; отдельно здесь надо отметить один момент касательно работы с интерфейсом к Maxima в редакторе TeXmacs: символы inf и minf при выводе здесь отображаются в своей традиционной математической нотации, то есть как ∞ и −∞; символ вместо inf можно, кроме того, использовать еще и при вводе.

Второй вариант вызова функции limit() — это расширенная версия первого: limit(выражение, переменная, точка, направление) , для поиска односторонних пределов. Для предела справа в качестве «направления» указывается plus , для предела слева — minus :

Пределы справа и слева еще иногда называют соответственно пределами сверху и снизу. Хотя правильнее в таком случае говорить полностью: «предел при x , стремящемся к a сверху», в том числе чтобы не создавать путаницы с верхним и нижним пределами, которые суть совершенно другое.

Кроме упомянутых выше бесконечностей, на выходе возможно появление и еще двух обозначений, на случай, если заданный предел не существует: ind (от слова indefinite — неопределенный) и und (от слова undefined — опять же неопределенный). В документации первое из этих обозначений описано как indefinite but bounded (не определен, но ограничен), что дает предположить, что функция, не имеющая предела, при этом ограничена либо в окрестности предельной точки, либо на всей прямой. Какое из этих предположений имелось в виду, мне так и не удалось понять, потому как на практике ни одно из них не соответствует действительности. Вывода ind мне не удалось добиться ни на одной функции, радикально отличающейся от «канонической» (в том смысле, что фигурирующей в стандартном примере из комплекта) функции sin(1/x) .

Здесь все правильно, tan(1/x) не ограничена в окрестности нуля. А вот дальше начинаются чудеса:

Как видите, первая функция имеет конечные односторонние пределы в нуле, а вторая ограничена вообще на всей оси — и тем не менее… Но это, думаю, не столь критично: главное, что наличие любого из этих символов в качестве вывода дает нам понять, что искомого предела не существует.

Функция limit() в третьем варианте — limit(выражение) — предназначена уже не для поиска собственно пределов, а для упрощения выражений, содержащих символы inf и minf :

Выражения такого рода могут возникать, к примеру, при подстановках в формулы результатов вычисления каких-то других пределов или интегралов.

Такая способность — принимать различные списки аргументов — не является в Maxima чем-то особенным; она свойственна очень многим встроенным функциям, как и различное действие в зависимости от значений разнообразных переключателей. Это достаточно удобно: не нужно запоминать много разных имен функций (для поиска пределов, к примеру, используется исключительно функция limit ); для вычисления производных, в том числе и частных, — функция diff (с которой мы уже бегло ознакомились в первой статье и сейчас продолжим это знакомство); для нахождения интегралов, как определенных, так и неопределенных — функция integrate (с которой мы тоже сегодня познакомимся). Имена наиболее часто используемых функций запомнить несложно, а о дополнительных ключах или флагах, в случае чего, можно прочитать во встроенной справке, набрав ? имя-функции .

Об этих самых ключах к функции limit и осталось рассказать. Первый ключ называется lhospitallim и задает максимальное количество применений правила Лопиталя; название ключа и происходит от фамилии ученого, давшей название самому правилу, которая в оригинале пишется как L’Hospital. Напомню, правило это гласит, что в случае неопределенности вида 0/0 или можно продифференцировать числитель и знаменатель — и предел от этого не изменится. Ограничитель количества применений этого правила нужен для того, чтобы избежать зацикливаний, которые могут случиться для бесконечно дифференцируемых функций, у которых в данной точке равны нулю либо бесконечности все производные. По умолчанию значение lhospitallim равно четырем, и мне не удалось сходу придумать пример, когда этого не хватает — ведь функция поиска предела использует не только правило Лопиталя, но и другие соотношения; и для всех заданных мною соотношений двух функций с корнями выше четвертого порядка в искомой точке предел был успешно найден и при умолчательном значении.

Второй ключ к функции limit — это флаг limsubst , который, будучи выставлен в true , позволяет этой функции производить подстановки внутрь неизвестных выражений. По умолчанию этот флаг равен false , что исключает ошибки вроде такой:

И, наконец, последний дополнительный параметр — еще один флаг, по имени tlimswitch . По умолчанию он тоже выключен, а если его включить, функция limit будет, при невозможности найти предел другими способами, пытаться его найти путем разложения подпредельной функции в ряд Тейлора в окрестности заданной точки:

Но в случае поиска односторонних пределов, в тех точках, где они не равны между собой, то есть полного предела не существует, этим флагом нужно пользоваться с осторожностью: при его включении функция limit может вернуть в качестве полного предела один из односторонних:

Реально у этой функции в точке ноль только предел справа равен единице; а предел слева — нулю.

И последнее: почему я употребил в начале по отношению к функции limit() слово «полноценная». Потому что кроме нее существует еще одна «недофункция» — tlimit() ; она представляет собой фактически просто-напросто вызов самой функции limit() с поднятым флагом tlimswitch , то есть пытается при необходимости разложить «подпредельную» функцию в ряд Тейлора вне зависимости от реального значения этого флага. Другими словами вызов tlimit(аргументы) полностью аналогичен записи limit(аргументы) , tlimswitch:true ; только чуть короче. И аргументы она может принимать точно такие же.

…дифференцируем и интегрируем

О функции diff я кое-что уже рассказывал в первой статье, и здесь это «кое-что» только напомню. В двух упомянутых тогда вариантах вызова эта функция принимала один либо два аргумента. С двумя, diff(выражение, переменная) , она возвращает производную от «выражения» по заданной переменной; с одним, diff(выражение) — полный дифференциал заданного выражения. Другими словами, запись diff(f, x) равнозначна математическому обозначению d f /d x , а diff(f) — d f .

Но это еще не все. Кроме одного либо двух, эта функция может также принимать любое нечетное число агрументов вида diff(выражение, переменная, порядок, переменная, порядок, …) и возвращает при этом производную либо смешанную частную производную от выражения заданных порядков по заданным переменным. К примеру, diff(f, x, 3) означает d 3 f /d x 3 , а diff(f, x, 1, y, 2, z, 1) — d 4 f /d x d y 2 d z . Единственный флаг, имеющий прямое отношение к самой функции diff — это флаг derivabbrev, который влияет на отображение производных в ячейках вывода Maxima. По умолчанию он равен false , и производные обозначаются в виде дробей с буквой d; если же его выставить в true , производные будут отображаться в сокращенном виде, с переменными дифференцирования записанными в виде индексов:

Кроме того, функция diff используется еще и для обозначения производных в дифференциальных уравнениях. Но об этом чуть позже, а сейчас перейдем к интегрированию.

Основная функция интегрирования называется, как я уже говорил, integrate и имеет два варианта вызова: для нахождения неопределенного и определенного интегралов. Первый выглядит как integrate(выражение, переменная) , второй — как integrate(выражение, переменная, нижний-предел, верхний-предел) :

Вы, наверное, обратили внимание еще на один момент в ячейках %i4 – %o4 . Когда в выражении используется какой-либо независимый символ, результат, вообще говоря, может зависеть от значения этого символа. Если при этом о возможных значениях символа ничего не известно, то Maxima задаст вам один или несколько вопросов об этом значении, и решение будет искать в зависимости от ваших ответов на них. Так, в этом примере значение определенного интеграла напрямую зависит от знака параметра a:

Кроме обычных определенных интегралов Maxima умеет искать также и несобственные интегралы, то есть такие, у которых неограничена либо область интегрирования, либо подынтегральная функция; и делается это все той же функцией integrate :

В случае, если искомый интеграл не сходится, будет выдано сообщение об ошибке, говорящее о том, что интеграл расходящийся:

В случае, если интеграл не может быть найден, он либо целиком возвращается в несовершенном виде, либо упрощается частично и на выходе получается некоторая формула, включающая в несовершенном виде интеграл той части подынтегрального выражения, которую проинтегрировать не удалось:

Кроме функций diff и integrate , в Maxima есть еще много разнообразных возможностей, связанных с производными и интегралами, в частности, функции для численного расчета значений определенных интегралов, а также инструменты, применимые при работе с дифференциальными и интегральными уравнениями. И разнообразны они настолько, что для того, чтобы рассмотреть подробно и с примерами их все, не хватило бы всего этого цикла. А более тезисно, хотя и на английском языке, они описаны в документации. Посему с этой темой на этом прекращаем и движемся дальше.

Решайте, сударь!

А дальше мы рассмотрим уравнения и их системы, и даже не столько рассмотрим, сколько порешим… то есть, конечно, порешаем. Уравнения и системы уравнений решаются в Maxima тоже одной и той же функцией, и тоже уже вам слегка знакомой по первой статье: это функция solve . Но прежде чем рассмотреть ее подробнее, нужно сказать пару слов о списках, или векторах, в Maxima; поскольку именно в виде списков solve возвращает корни, да и принимает параметры в случае решения системы уравнений, а не одного уравнения.

Синтаксис списков в Maxima весьма прост; это перечисление элементов в квадратных скобках: [элемент1, элемент2, …, элементN] . Особенность — не в синтаксисе. Основное достоинство Maximaльных списков в том, что их элементами могут быть совершенно любые выражения: символы, арифметические выражения, вызовы функций, присвоения, уравнения, другие списки… Додумать можете сами. Поэтому списки и во встроенных функциях применяются достаточно широко. Функция solve в своем простейшем варианте, для решения одиночного уравнения, в качестве аргументов никаких списков, напомню, не принимает (а принимает либо уравнение и символ, относительно которого его надо решать, либо только уравнение, если символ в нем всего один). А вот в качестве результата она уже и в таком варианте возвращает список, состоящий из всех корней заданного уравнения:

Как видите, функция solve находит все комплексные корни уравнения, а не только действительные.

К элементу списка можно обратиться с помощью тех же квадратных скобок, указав в них номер элемента после имени списка. Напомню, что равенство, переданное в качестве дополнительного параметра функции ev, означает подстановку переменной в вычисляемое выражение. Вот так мы можем осуществить проверку решения, подставив корень из выданного списка в исходное уравнение:

Точно таким же образом можно обратиться и к любому другому элементу списка:

Вообще говоря, в качестве первого аргумента функции solve можно задавать не только уравнение, а вообще любое выражение. При этом «корни выражения» (не являющегося уравнением) ищутся в том самом смысле, в каком эта фраза понимается в математике: корни выражения — это те значения переменной, на которых выражение обращается в ноль. Возможность такой записи позволяет, к примеру, легко найти критические точки любой непрерывной функции (а заодно и вычислить значения функции в этих точках):

В этом примере есть еще два важных момента. Первый — функция %th() . Она, как видно из контекста, вызывается как %th(n) и возвращает n -ю с конца ячейку вывода. Это, так же как и обозначения % и _ , удобно, чтобы не обращать внимания на номера ячеек, и кроме того, применимо в командных файлах Maxima, которые могут загружаться в том числе и прямо из интерактивной сессии (с помощью функции load ) — и тогда просто заранее неизвестно, начиная с какой ячейки данный файл загружен. И второй момент: здесь проиллюстрировано, что в Maxima операция индексирования списка доступна не только по отношению к именам переменных, но и к вызовам функций; другими словами, если функция возвращает список значений, мы можем выбрать одно конкретное из них, написав его номер в квадратных скобках прямо после вызова функции.

Вернемся к функции solve . А именно, перейдем теперь к решению систем уравнений. Для этого существует такой вариант записи: solve([уравнение1, уравнение2, …], [переменная1, переменная2, …]) ; либо сокращенный, аналогично варианту для одиночного уравнения: если количество уравнений и количество неизвестных равны, список неизвестных можно не писать: solve([уравнение1, уравнение2 …]) (не забудьте квадратные скобки, иначе Maxima примет его за вариант с одним уравнением).

Здесь возвращается список из нескольких списков, каждый из которых соответствует одному решению системы. В качестве подстановок можно использовать как такие списки целиком (например, в данном контексте, %o1[1] ), так и отдельные их элементы (например, %o1[1][1] ).

В случае, когда уравнений меньше, чем неизвестных, solve поступит точно так же, как и в случае одного уравнения с несколькими символами: все неуказанные будет воспринимать как параметры:

Если solve не находит точных решений, она может, как и integrate , вернуть уравнение или систему уравнений в некотором упрощенном виде, а может и самостоятельно попытаться решить систему численно:

В таком случае, если вам все же нужны точные значения корней (в аналитической записи), либо если они не найдены даже в числах, можно попробовать решить уравнения по очереди, выражая одно неизвестное через другое:

И подставляя в оставшиеся уравнения:

Теперь можем подставить обратно — и найти значения второй неизвестной, например, для первого и последнего корней из последнего списка:

Функция solve имеет довольно большое количество различных переключателей, из которых может пригодиться в своем не-умолчательном значении в первую очередь один: solveradcan . Умолчание здесь равно false , а выставив этот флаг в true , мы заставим solve , помимо его умолчательного поведения, применять radcan — функцию по упрощению показательных, логарифмических и степенных (с рациональными степенями) функций. Это делает работу функции solve более медленной (потому по умолчанию этот режим и выключен), но в некоторых случаях может помочь разрешить проблемы, которые без этого ключа приведут к невозможности найти точное решение.

И снова дифференцируем и интегрируем

Помимо «просто» уравнений, Maxima позволяет также решать и обыкновенные дифференциальные уравнения первого и второго порядка. Функций, непосредственно занимающихся решением таких уравнений, существует две. Первая из них занимается поиском частных решений линейных дифференциальных уравнений и систем таких уравнений; зовут ее desolve , от слов differential equation solve. Эта функция принимает два аргумента, первый из которых — уравнение либо список уравнений, а второй — соответственно одна переменная или список переменных. Если не заданы значения функций и/или их производных в нуле, то в найденном решении они просто отображаются в виде f(0) или

задать эти значения позволяет функция atvalue(выражение, переменная = точка, значение) ; то есть, в данном случае atvalue(f(x), x=0, значение) или atvalue(‘diff(f(x)), x=0, значение) . Производные в уравнениях и системах, решаемых с помощью этой функции, должны быть записаны непременно в виде ‘diff(f(x), x) , а не просто ‘diff(f, x) , а сами функции, соответственно, тоже в виде f(x) , а не f — нужно продемонстрировать зависимость функции от ее аргумента.

И конечно же, точно так же как для обычных уравнений и систем, здесь мы тоже можем проверить решение с помощью подстановки, но только надо еще дополнительно задать принудительное вычисление производных, так как в уравнениях они фигурируют в несовершенной форме:

Вторая функция из этой группы называется ode2 и предназначена она для решения обыкновенных дифференциальных уравнений первого и второго порядка; ее название происходит от фразы ordinary differential equations of 1st or 2nd order. Пишется она так: ode2(уравнение, зависимая-переменная, независимая-переменная) . Здесь уже независимая переменная указывается в списке параметров функции явно, и потому обозначения вида y(x) не нужны: и функция, и переменная обозначаются просто одиночными буквами. Также в отличие от предыдущей функции, ode2 ищет не частное, а общее решение. Произвольная константа в решении уравнения первого порядка обозначена через %c ; в решении уравнения второго порядка таких констант, естественно, две, и обозначаются они как %k1 и %k2 .

В дополнение к функции ode2 существуют три функции для поиска частных решений на основе полученных общих. Иначе говоря, эти функции, получая конкретные условия относительно значения функции-решения в заданной точке, находят исходя из этих значений соответствующие им величины интегральных констант. Одна из этих функций предназначена для обработки решения дифференциального уравнения первого порядка. Она называется ic1 (i от initial value — начальное значение; c от constant — константа; 1 от 1 st order — первого порядка) и принимает три аргумента: первый — само решение, в том виде, в котором его находит функция ode2 ; второй — значение независимой переменной ( x -координаты), третий — значение функции (зависимой переменной, у ) при этом значении x и возвращает частное решение, проходящее через точку с заданными координатами ( x , y ):

И две функции работают с решениями уравнений второго порядка. Так как в общем решении уравнения второго порядка фигурируют две независимые константы, то эти функции задают уже по два условия для поиска частного решения. Первая функция выглядит как ic2(общее решение, x, функция-в-точке-x, производная-в-точке-x) . Расшифровка названия аналогична предыдущей функции. Действует тоже аналогично ей, а в качестве второго условия задает значение производной в той же заданной точке:

И последняя функция называется bc2 (b от boundary value — граничное значение; а дальше все как в предыдущей). Ее аргументы: первым, как и в двух остальных вариантах, идет само общее решение, возвращенное функцией ode2 ; после него идут две пары значений: x ₀, y ₀, x ₁, y ₁, задающие две точки, через которые должен проходить график функции-решения:

Касательно дифференциальных уравнений все этими функциями и заканчивается, никаких дополнительных ключей к ним не предназначено.

В следующий раз мы поговорим о средствах построения графиков функций и о средствах автоматизации: условных операторах, циклах и управляющих условиях, налагаемых на различные символы и выражения.

Вопросы о Maxima или этого сайта: Списки рассылки

«Т. Н. Губина, Е. В. Андропова РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В СИСТЕМЕ КОМПЬЮТЕРНОЙ МАТЕМАТИКИ MAXIMA Учебное пособие Елец — 2009 УДК 519.62+519.63+004.94 ББК 32.973.26-018 Г 93 . »

5 шаг. Находим решение, используя разностную схему Также можно использовать и неявные разностные схемы. В этом случае частные производные заменяются конечно-разностными аппроксимациями, но u i1, j не выражаются в явном виде через значения на предыдущих слоях. Для определения u i1, j на каждом временном шаге необходимо решать систему уравнений. При использовании неявных схем можно вести вычисления с достаточно большим шагом.

Преимущество неявных схем перед явными в том, что в неявных схемах шаг сетки можно сделать достаточно большим, не опасаясь, что ошибки округления «разрушат» решение.

ГЛАВА 3 НАХОЖДЕНИЕ РЕШЕНИЙ

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В

СИСТЕМЕ MAXIMA

3.1. Встроенные функции для нахождения решений дифференциальных Перейдем к более подробную рассмотрению функций и команд, с помощью которых можно находить решения дифференциальных уравнений.

Система компьютерной математики Maxima может с успехом решать следующие виды дифференциальных уравнений первого порядка: с разделяющимися переменными, линейные, нелинейные уравнения, однородные, неоднородные. Виды уравнений второго порядка: с постоянными коэффициентами, линейные однородные с непостоянными коэффициентами, которые могут быть преобразованы к уравнению с постоянным коэффициентам, уравнение Эйлера, уравнения, разрешимые методом вариации постоянных, и уравнения, которые допускают понижение порядка.

Рассмотрим команды системы Maxima для нахождения решений дифференциальных уравнений и их систем в символьном виде:

desolve (eqn, x) — ищет частные решения линейных дифференциальных уравнений первого и второго порядков desolve ([eqn_1. eqn_n], [x_1. x_n]) (сокращенно от слов «differential equation solve») — ищет частные решения систем линейных дифференциальных уравнений первого и второго порядков.

Эта функция принимает два аргумента, первый из которых – уравнение либо список уравнений, а второй – соответственно одна переменная или список переменных.

Если не заданы значения функций и/или их производных в нуле, то в дать эти значения позволяет функция atvalue(выражение, переменная=точка, значение), то есть, в данном случае atvalue(f(x),x=0, значение) или atvalue(‘diff(f(x),x)=0, значение). Производные в уравнениях и системах, решаемых с помощью этой функции, должны быть записаны в виде ‘diff(f(x),x).

Если функция desolve не может найти решения, то она возвращает значение false.

ode2(eqn, dvar, ivar) — предназначена для решения обыкновенных линейных дифференциальных уравнений первого и второго порядка. Решение ищется в общем виде. Принимает три аргумента: eqn – само дифференциальное уравнение, зависимая переменная dvar, и независимая переменная ivar. Данная функция может возвращать решение в явном и неявном виде.

Здесь уже зависимая переменная указывается в списке параметров функции явно, поэтому обозначения вида y(x) не нужны. Функция и переменная обозначаются одиночными буквами.

Как и для обычных уравнений и систем, мы можем проверить решение с помощью подстановки, но только надо еще задать принудительные вычисления производных, так как в уравнениях они фигурируют в несовершенной форме.

Произвольная константа для уравнений первого порядка обозначается через %c. В уравнениях второго порядка константы обозначаются как %k1 и %k2.

Если функция ode2 не может получить решение по какой-либо причине, то она возвращает значение false, при этом возможен вывод сообщения об ошибке.

В дополнение к функции ode2 существуют три функции для поиска частных решений на основе полученных общих. То есть, эти функции, получая конкретные условия относительно значения функции-решения в заданной точке, находят исходя из этих значений соответствующие им величины интегральных констант. Перечислим их.

ic1(solution, xval, yval) — предназначена для обработки решения дифференциального уравнения первого порядка с начальными условиями. Принимает три аргумента: первый – само решение, в том виде, в котором его находит функция ode2, второй – начальное значение независимой переменной в форме x = x0, третий – значение функции yval при указанном значении xval в виде y = y0. Возвращает частное решение, проходящее через точку с заданными координатами (xval, yval).

ic2(solution, xval, yval, dval) — предназначена для обработки решения дифференциального уравнения второго порядка с начальными условиями.

Принимает четыре аргумента: solution — общее решение уравнения, найденное с помощью функции ode2, xval — начальное значение независимой переменной в форме x = x0, yval — начальное значение зависимой переменной в форме y = y0, и dval — начальное значение для первой производной зависимой переменной относительно независимой переменной, в форме (y, x)= dy0.

bc2(solution, xval1, yval1, xval2, yval2) — предназначена для нахождения решения граничной задачи для дифференциального уравнения второго порядка. Здесь solution — общее решение уравнения, найденное с помощью функции ode2, xval1 — значение независимой переменной в первой граничной точке, задается в виде x=x1, yval1 — соответственно значение зависимой переменной в точке x, задается также в виде y=y1, xval2, yval2 – вторая граничная точка, задается в той же форме, что и первая точка.

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Функция plotdf позволяет строить траектории и поле направлений дифференциального уравнения первого порядка или автономной системы двух обыкновенных дифференциальных уравнений первого порядка. Эта функция входит в дополнительный пакет, поэтому для ее использования следует первоначально его загрузить командой load(plotdf). Функция Plotdf требует установки модуля Openmath, который входит в пакет xMaxima.

Для построения поля направлений дифференциального уравнения перdy Синтаксис функции:

plotdf(dydx. options. ) plotdf(dvdu, [u,v]. options. ) plotdf([dxdt,dydt]. options. ) plotdf([dudt,dvdt], [u,v]. options. ) Здесь dydx, dxdt и dydt — выражения, которые зависят от x и y, dvdu, dudt и dvdt — выражения, которые зависят от u и v. В дополнение к этим двум переменным, могут использоваться опции. Они могут выбираться с помощью пунктов меню, а также задаваться с помощью специальных команд.

В системе Maxima есть дополнительный пакет contrib_ode, который позволяет находить решение нелинейных дифференциальных уравнений первого и второго порядка.

Для того чтобы можно было использовать команды этого пакета, его необходимо сначала подключить с помощью команды load(contrib_ode).

Заметим, что возможности пакета contrib_ode расширяются с каждой новой версией системы Maxima.

Синтаксис команды: contrib_ode (eqn, y, x) Для корректного выполнения поиска решения с использованием команды contrib_ode ей нужно передать три аргумента:

1. Само дифференциальное уравнение, которое требуется решить (в правой части дифференциального уравнения должен стоять ноль) 2. Имя зависимой переменной — искомой функции 3. Имя независимой переменной — аргумента функции.

Если дифференциальное уравнение система может решить, то она возвращает решение или список решений, причем каждое решение может быть представлено в одном из следующих видов:

1. Искомая функция выражена в явном виде.

2. Искомая функция выражена в неявном виде.

3. Решение получено в параметрическом виде с параметром t%.

4. Дифференциальное уравнение преобразуется к другому дифференциальному уравнению относительно функции u%.

В случае, если решение не может быть получено, команда contrib_ode возвращает сообщение об ошибке и значение «false».

3.2. Решение дифференциальных уравнений и их систем в символьном Рассмотрим ряд примеров на нахождение решений дифференциальных уравнений с помощью встроенных функций системы.

Пример 1. Найти частное решение дифференциального уравнения с разделенными переменными sin x dxdy=0 при начальном условии y 0=4.

Решение. Для решения уравнения в системе Maxima выделим производную функции y явно, поделив обе части уравнения на dx : sin x y ‘ =0.

Зададим уравнение в строке ввода и обозначим его eqn.

Зададим начальное условие y 0=4 :

Теперь задаем команду для нахождения искомого частного решения:

В том случае, если не задать предварительно начальные условия, то система выдаст ответ в виде:

Как видно, если мы подставим условие y 0=4, то решения совпадут.

Пример 2. Найти частное решение линейного дифференциального уравнения первого порядка 5 y ‘8 y= x при условии y 0=1.

Решение. Зададим уравнение под именем eqn и начальное условие (заметим, что знак умножения нужно прописывать каждый раз явно):

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Теперь воспользуемся командой desolve для поиска частного решения:

Пример 3. Найти частное решение системы линейных дифференциальf ‘ ( x) = g ‘ ( x) + sin x Решение. Зададим каждое из уравнений системы.

Зададим начальные условия:

Ищем частное решение:

Для нахождения общего решения дифференциального уравнения в системе Maxima используется команда ode2. Рассмотрим ряд примеров.

Пример 4. Найти общее решение линейного дифференциального уравdy нения первого порядка x 1 способ. Зададим уравнение в ячейке ввода.

Теперь решим уравнение. Для этого в ячейке ввода задаем команду ode2(eq1, y(x), x) и оцениваем. В результате получим:

2 способ. В нижней части окна программы на панели инструментов нажимаем на кнопке Решить ОДУ. Появляется диалоговое окно, в котором надо задать само дифференциальное уравнение, имя искомой функции и имя независимой переменной:

После нажатия на кнопке OK получаем решение:

Как видим, решения совпали.

В некоторых случаях система может выдавать решения в неявном виде — в виде общего интеграла.

Пример 5. Найти общее решение дифференциального уравнения Решение. Задаем дифференциальное уравнение Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Решаем уравнение:

Пример 6. Найти общее решение уравнения Бернулли y ‘ 2 e x y=2 e x y.

Решение. Задаем уравнение и обозначаем его eqn.

В том случае, если система не может решить дифференциальное уравнение, она возвращает значение false или выдает сообщение об ошибке.

Пример 7. Найти общее решение уравнения Клеро y=x y ‘ y ‘ 2.

Решение. Зададим уравнение и воспользуемся командой ode2 для его решения.

Рассмотрим ряд примеров на нахождение решений обыкновенных дифференциальных уравнений первого порядка с начальными условиями.

Для этого используется команда ic1.

Пример 8. Найти общее решение дифференциального уравнения 2 x y ‘ =x y и найти его частное решение, удовлетворяющее начальному условию y 1=0.

Решение. Найдем общее решение дифференциального уравнения и обозначим его rez.

Теперь воспользуемся условием y 1=0.

Как видно, система нашла решение в неявном виде. Разрешим полученное уравнение относительно y и тем самым найдем решение в явном виде.

Пример 9. Найти частное решение дифференциального уравнения xx y dy yx y dx=0 при y 1=1.

Решение. Аналогично предыдущему примеру, ищем общее решение дифференциального уравнения.

Далее находим частное решение.

Пример 10. Решить задачу Коши для дифференциального уравнения Решение. Находим решение задачи Коши с помощью команды ic1.

Для упрощения полученного результата разрешим его относительно y.

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Для нахождения решений дифференциальных уравнений второго порядка используются те же команды, что и для уравнений первого порядка.

Однако при решении начальной и граничной задач используются другие команды. Рассмотрим на примерах.

Пример 11. Найти общее решение дифференциального уравнения второго порядка 15 y ‘ 26 y= y ‘ ‘.

Решение. Зададим исходное уравнение:

Для поиска общего решения используем команду ode2.

Выполним проверку найденного решения. Для этого зададим команду в следующем виде:

Из полученного ответа не видно, правильно ли было получено решение. Упростим полученный результат.

Отсюда видно, что левая часть уравнения eqn равна его правой части, следовательно, решение было найдено правильно.

Пример 12. Найти общее решение дифференциального уравнения второго порядка y ‘ ‘6 y ‘ 9 y=0.

Решение. Зададим исходное уравнение:

Находим его решение.

Пример 13. Найти общее решение дифференциального уравнения второго порядка y ‘ ‘2 y ‘ 10 y=0.

Решение. Зададим исходное уравнение:

Находим его решение.

Пример 14. Решить задачу Коши для дифференциального уравнения Решение. Зададим уравнение и обозначим его eqn.

Воспользуемся командой ic2 для нахождения решения начальной задачи для дифференциального уравнения второго порядка.

Попробуем упростить полученное решение, применив команду раскрытия выражения expand.

Выполним проверку найденного решения.

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Упростим результат после подстановки решения в исходное уравнение.

Таким образом, решение найдено правильно.

Пример 15. Найти решение уравнения y ‘ ‘ y= x, удовлетворяющее краевым условиям y 0=0, y 4=1.

Решение. Зададим исходное уравнение.

Найдем общее решение уравнения.

Воспользуемся командой bc2 для решения краевой задачи.

Пример 16. Решить дифференциальное уравнение: y ‘ 2x y y ‘=0.

Подключим пакет contrib_ode и зададим дифференциальное уравнение eqn. Найдем решение дифференциального уравнения и запомним его под именем ans. Убедимся в правильности найденного решения. Для этого воспользуемся командой ode_check и выполним проверку найденных решений.

Пример 17. Решить дифференциальное уравнение: y ‘ 2x y ‘ y =0.

Как видим, решение получено в параметрическом виде. С помощью команды method можно посмотреть метод, примененный для нахождения решения дифференциального уравнения:

Пример 18. Решить дифференциальное уравнение: y ‘ = x y2.

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima 3.3. Построение траекторий и поля направлений дифференциальных Пример 1. Построить интегральную кривую дифференциального уравdy x нения dx =e y, проходящую через точку 2,0.1, и поле направлений.

Подключим пакет plotdf с помощью команды load(plotdf)$. Зададим команду для построения интегральной кривой уравнения и поля направлений.

В результате у нас будут образованы две ячейки ввода с именами (%i1) и (%i2).

После оценивания ячейки ввода %i2 откроется окно программы OpenMath с результатом выполнения команды.

Как видно, окно имеет несколько пунктов меню для работы с графическим изображением. Меню Масштабировать позволяет увеличивать и уменьшать график. Меню Настройка позволяет изменять некоторые установки: решаемое уравнение, начальная точка и направление вычисляемой траектории, шаг интервала интегрирования и др. С помощью меню Сохранить может быть сохранен построенный график в PostScipt файл.

Пример 2. Построить интегральную кривую и поле направлений систеdz Построим интегральную кривую, определенную этими двумя уравнениями и проходящую через точку (z, v) = (6,0). Установим начальные значения параметра m второго уравнения системы равным 2. Воспользуемся опцией slider, которая позволит нам изменять значения параметра m в интерактивном режиме с помощью бегунка в левом нижнем углу графического окна.

Вводим две команды:

В результате получаем:

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Как видно из построений, начальное значение параметра m установлено равным 2. Передвигая бегунок полосы прокрутки, мы можем менять исходную систему, а соответственно и фазовый портрет системы:

Пример 3. При каких значениях параметра a особая точка системы только одна и является седлом? узлом? фокусом? Дать чертеж траекторий при a=8.

Составим характеристическое уравнение и найдем его корни. Для этого зададим матрицу. Выберем пункт меню Алгебра –Enter Matrix (Ввести матрицу). Появится диалоговое окно, запрашивающее размерность матрицы.

После задания размерности нажимаем OK и в следующем диалоговом окне вводим элементы матрицы:

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima При нажатии на кнопке OK создаются ячейки ввода и вывода с матрицей.

Вычислим определитель матрицы и найдем собственные значения матрицы.

Вычислим произведение собственных значений матрицы 1 2 :

Так как система Maxima не умеет решать неравенства в символьном виде, то определим графически знак полученного произведения 1 2 при различных значениях параметра a. Для этого воспользуемся пунктом меню Графики-Plot 2d (График 2D), заполним значения полей в появившемся диалоговом окне следующим образом (при выборе формата Встроенный график будет располагаться не в отдельном окне, а в самом документе):

В результате получим следующее построение:

Из графика видно, что 1 2 =4a12= = 0 при a=3. Остается посмотреть на знак дискриминанта и определить, при каких значениях a собственные значения являются действительными, а при каких комплексными, числами.

Вычислим дискриминант выражения d, предварительно представив его в виде квадратного трехчлена:

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Определим знак дискриминанта при различных значениях параметра Тогда, согласно классификации особых точек [см., например, 1, с.112получаем:

1. При a3 имеем 1 2 0, особая точка – седло.

2. При a=3 имеем 1=0, 2 =4, особых точек много.

3. При 3a4 корни вещественные, 1 2 0, особая точка устойчивый узел (при a=4 — вырожденный узел).

4. При a4 корни комплексные, особая точка устойчивый фокус.

Подтвердим рассуждения построениями. Построим поле направлений для исходной системы уравнений, положив, что значение параметра a меняется от -8 до 10, тем самым мы сможем, изменяя положение бегунка полосы прокрутки, просмотреть все возможные варианты особых точек. За начальТ.Н. Губина, Е.В. Андропова ное значение параметра a возьмем значение равное 8 (согласно условию задачи). Задаем команду для построения поля направлений:

В результате у нас откроются два графических окна – одно с изображением поля направлений и траекторией, проходящей через точку (2,1), второе – с изображением значений функций x[t] и y[t] параметра t (чтобы это окно убрать, необходимо из строки для построения поля направлений удалить команду [versus_t,1]).

Для большей наглядности добавим еще несколько траекторий в окне поля направлений (щелкая левой кнопкой мыши в поле направлений) и тем самым убедимся в том, что у нас особая точка является устойчивым фокусом.

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Передвинем бегунок полосы прокрутки в позицию меньше 3. Получим геометрическую картину, называемую седлом.

При a, изменяющемся от 3 до 4, имеем устойчивый узел.

Для значения параметра a=3 изменим команду plotdf следующим образом.

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Как видно из построений, система дифференциальных уравнений действительно имеет множество особых точек.

3.4. Реализация численных методов решения задачи Коши для обыкновенных дифференциальных уравнений Во второй главе пособия были рассмотрены численные методы решения обыкновенного дифференциального уравнения первого порядка и приведены примеры решения одной задачи Коши методами Эйлера, Эйлера-Коши, Рунге-Кутта.

отрезке [0,1] с шагом h=0.2. Найти точное решение задачи и найти величину абсолютной погрешности в указанных точках.

Решим поставленную задачу с помощью системы Maxima и сравним полученные результаты.

Зададим концы отрезка, на котором будем искать решение, и шаг:

Найдем количество точек разбиения отрезка с шагом h :

Сформируем два пустых одномерных массива размера n1 для хранения значения координат точек [ x, y ] искомого решения:

Зададим начальное условие:

Для этого используем цикл с параметром.

Используя расчетную формулу Эйлера () главы 2, заполним массив Выведем полученное решение на экран:

Выполним построение ломаной Эйлера (найденного решения задачи (4.1)) средствами пакета draw:

Для нахождения точного решения задачи Коши воспользуемся встроенной командой desolve. Дифференциальное уравнение запомним под именем eq1:

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Задаем начальное условие:

Находим точное решение задачи Коши (4.1):

Вычислим значения функции в точках отрезка [0,1] с шагом h=0.2.

Найдем величину абсолютной погрешности:

Для решения задачи (4.1) методом Эйлера сформируем еще три пустых массива x2, y2 и вспомогательный массив z.

Зададим начальное условие:

Заполним массив x 2 значениями, начиная с 0.2 до 1 с шагом h.

Для этого используем цикл с параметром.

Теперь воспользуемся расчетной формулой Эйлера-Коши и найдем решение:

Выведем найденное решение на экран:

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Выполним построение найденного решения задачи (4.1) средствами пакета draw:

Найдем величину абсолютной погрешности:

В системе Maxima для нахождения численного решения задачи Коши методом Рунге-Кутта (четвертого пордяка точности) есть встроенная функция rk. Для того, чтобы она стала активной, требуется подключить пакет dynamics с помощью команды:

Теперь задаем команду для нахождения решения:

Выполним построение найденного решения задачи (4.1) средствами пакета draw:

Можно выполнить построение всех трех интегральных кривых в одной системе координат.

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima Как видим, метод Эйлера дает самое плохое приближение к точному решению задачи Коши (4.1).

3.5. Реализация конечно-разностного метода решения краевой задачи для обыкновенных дифференциальных уравнений Постановка задачи (5.1): Найти решение уравнения y ‘ ‘2y’ x =5 на ( n=3 ) с начальными условиями [0,4 ; 0,7] Решение задачи (5.1.) было рассмотрено во второй главе. Здесь же выполним решение краевой задачи конечно-разностным методом в системе Maxima.

Вводим обозначения и задаем значения переменных:

Разбиваем отрезок [a, b] на равные части с шагом h=0.1, n=3.

Формируем список, содержащий все точки отрезка:

Сформируем пустую квадратную матрицу a размера n1 :

Теперь заполним матрицу а по формулам:

Для заполнения коэффициентами первых двух уравнений системы воспользуемся циклом с параметром:

В двух последних уравнениях поменяем значения некоторых элементов с помощью оператора присваивания:

Теперь заполним столбец свободных членов:

Выведем полученные матрицы на экран:

Получили систему линейных уравнений, записанную в матричном виде ay=b, где y — искомое решение. Найдем его матричным способом.

Глава 3 Нахождение решений дифференциальных уравнений в системе Maxima 3.6. Реализация метода сеток для дифференциальных уравнений в частных производных Во второй главе мы рассмотрели суть метода сеток для нахождения численных решений дифференциальных уравнений в частных производных.

Выполним реализацию конечно-разностного метода в системе компьютерной математики Maxima.

значений U i, j размера mn.

Задаем значения a=1, k =0,1.

Заполняем первую и вторую строки массива U начальными условиями u x,0=sin, ut x,0=0 ( нулевой начальной скорости соответствует совпадение значений (смещений) в первом и втором столбцах).

Заполняем первый и последний столбец массива U граничными условиями u 0, t=u m, t=0 (на концах струны смещение равно нулю в любой момент времени).

Находим решение, используя разностную схему Для вывода полученного решения в виде поверхности преобразуем наш массив U в функцию двух переменных:

Теперь выполняем построение:

1. Найти решение дифференциального уравнения в Maxima:

2. Найти решение уравнения в Maxima, удовлетворяющее указанным начальным условиям. Построить график решения.

3. Найти решение дифференциального уравнения в Maxima:

4. Решить задачу Коши для дифференциального уравнения y ‘ = f x, y на отрезке [a, b] при заданном начальном условии y a =c с шагом h : методом Эйлера, методом Эйлера-Коши, методом Рунге-Кутты порядка.

5. Используя метод конечных разностей, найти решение краевой задачи для обыкновенного дифференциального уравнения второго порядка с шагом h=0,1.

6. Найти решение системы дифференциальных уравнений в Maxima:

7. Найти решение системы дифференциальных уравнений в Maxima:

8. Исследовать особые точки системы в Maxima. Начертить на фазовой плоскости траектории системы:

9. Методом сеток с шагом h найти приближенное решение волнового моугольной области [0, m][0, n ], используя явную разностную схему.

Граничные условия: на концах струны смещение равно 0 в любой момент времени: u 0, t=u m, t=0. Начальные условия:

0= m=0. Шаг изменения времени выбирается самостоятельно (так, чтобы разностная схема была устойчивой). Результат представить в виде поверхности.

a=1, m=39, n=45, h=1, x =0,2 x cos 10.Методом сеток с шагом h=1 пространственной переменной и = временной координаты найти приближенное решение уравнения тепu x,t u x, t квадрате [0, n][0, n], используя неявную разностную схему. Граничu 0, t= g 1 t= x=0, 0tn, виде поверхности.

11.Методом сеток с шагом h найти приближенное решение уравнения угольной области [0, a][0, b], используя явную разностную схему.

Граничные условия: u a,t =g1 t x=a,0tb.. Начальное условие:

u x,0= f xt=0,0xa.. Шаг изменения времени выбирается самостоятельно (так, чтобы разностная схема была устойчивой). Результат представить в виде поверхности.

a=40, D=2,b=60, h=1, f x=cos x, g 1 t=1, g 2 t =cos a=30, D=10, b=20, h=1, f x =sin x /2, g 1 t=0, g 2 t=sin 1. Додиер Р. Коротко о Maxima (пер. на русский Бешенов А), 2007. (ЭВ) 2. Житников В. Компьютеры, математика и свобода // Компьютерра, 3. Олейник О.А. Роль теории дифференциальных уравнений в современной математике и ее приложениях // Соросовский образовательный журнал, 1996, №4, с. 114-121.

4. С. Фарлоу. Уравнения с частными производными для научных работников и инженеров: пер. с англ./ под редакцией С.И. Похожаева. — М.: Мир, 1985. — 384 с.

Сливина Н.А. Профессиональные математические пакеты в образовании // Педагогические и информационные технологии в образовании. – № 2.

– http://scholar.urc.ac.ru:8002/Teachers/ methodics/journal/numero2/ slivina.html 6. Тарнавский Т. Maxima — алгебра и начала анализа // LinuxFormat, № 11, 2006 (ЭВ) 7. Тарнавский Т. Maxima — графики и управляющие конструкции // LinuxFormat, № 11, 2006 (ЭВ) 8. Тарнавский Т. Maxima — максимум свободы символьных вычислений // LinuxFormat, № 7, 2006. (ЭВ) 9. Тарнавский Т. Maxima — укротитель выражений // LinuxFormat, № 9, 2006 (ЭВ) 10. Тарнавский Т. Maxima — функции и операторы // LinuxFormat, № 8, 2006 (ЭВ)

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

В СИСТЕМЕ КОМПЬЮТЕРНОЙ МАТЕМАТИКИ MAXIMA

Формат 60 х 84 /16. Гарнитура Times. Печать трафаретная.

Отпечатано с готового оригинал-макета на участке оперативной полиграфии Елецкого государственного университета им. И.А.Бунина.

Государственное образовательное учреждение «Елецкий государственный университет им. И.А. Бунина»

«№ 2499 Методические указания для изучения курса ЭКОЛОГИЯ к выполнению контрольной работы для студентов всех специальностей заочной формы обучения Иваново 2006 В методических указаниях приведены содержание дисциплины, варианты заданий, список вопросов контрольной работы, варианты и условия задач с примерами их решения, содержание лабораторных работ по курсу, а также список рекомендуемой литературы. Составитель: Валентина Ивановна Яницкая Научный редактор А. М. Осипов 1. Цели изучения дисциплины. »

«Электронный учебно-методический комплекс Спецглавы высшей математики Авторы: доцент кафедры ВМ В.Г. Крупин, доцент кафедры ВМ И.В. Стаценко Направление 210400 Радиотехника, подготовки: профили: Радиотехнические средства передачи, приема и обработки сигналов; Аудиовизуальная техника; Бытовая радиоэлектронная аппаратура; Радиоэлектронные системы; Радиофизика Дисциплина: Спецглавы высшей математики (3,4 семестр) Адрес ресурса: Контактная Почтовые электронные адреса авторов ресурса, по которому. »

«В.Г. Крец, А.В. Шадрина ОСНОВЫ НЕФТЕГАЗОВОГО ДЕЛА ИЗДАТЕЛЬСТВО ТПУ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИНСТИТУТ МЕЖДУНАРОДНОГО ОБРАЗОВАНИЯ И ЯЗЫКОВОЙ КОММУНИКАЦИИ В.Г. Крец, А.В. Шадрина ОСНОВЫ НЕФТЕГАЗОВОГО ДЕЛА Учебное пособие Издательство Томского политехнического университета УДК 622. Крец В.Г., Шадрина А.В. Основы. »

«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Кафедра физики Кандауров И.В., Мезенцев Н.А., Мешков О.И., Мучной Н.Ю., Пиндюрин В.Ф., Симонов Е.А. МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ЯВЛЕНИЙ НА ЭВМ Методическое пособие Часть I Общие сведения о курсе Справочная информация по языку PASCAL Построение графиков функций Новосибирск 2000 Данное пособие является первым в серии учебно-методических материалов по специализированному курсу Моделирование физических явлений на ЭВМ. »

«Белорусский государственный университет Химический факультет Кафедра физической химии Л.А.Мечковский Л.М.Володкович Развернутая программа дисциплины “Физическая химия” с контрольными вопросами и заданиями Учебно-методическое пособие для студентов химического факультета специальности Н 03.01.00—химия Минск 2004 1 УДК. ББК. Рецензенты Кандидат химических наук доцент Г.С. Петров Кандидат химических наук доцент А.Ф. Полуян Мечковский Л.А., Володкович Л.М. Развернутая программа дисциплины. »

«ГЕОДЕЗИЯ С ОСНОВАМИ КОСМОАЭРОСЪЕМКИ (Учебно-методическое пособие) Казань, 2008 г. Казанский государственный университет Геологический факультет Кафедра геофизики Учебно-методическое пособие по спецкурсу Методы полевой геофизики для студентов геофизической и нефтяной специальностей. Печатается по постановлению учебно-методического совета геологического факультета КГУ. Протокол № 2008 года. Составители: Комаров Р. В., Минсафин Г.З. 2 СОДЕРЖАНИЕ Содержание -3 Тема 1. Основные понятия геодезии -. »

«Государственное образовательное учреждение высшего профессионального образования КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Гравиразведка учебно-методическое пособие для слушателей курсов повышения квалификации специальности Геофизика по программе Методы поисков и разведки месторождений полезных ископаемых в промысловой и разведочной геофизике Казань 2009 Утёмов Э.В. Гравиразведка Печатается по решению Редакционно-издательского совета ГОУ ВПО Казанский государственный университет им. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНСТРУКЦИЯ ПО СОДЕРЖАНИИЮ И ПОРЯДКУ СОСТАВЛЕНИЯ КУРСОВОЙ РАБОТЫ ПО КУРСУ СТРУКТУРНАЯ ГЕОЛОГИЯ И ГЕОЛОГИЧЕСКОЕ КАРТИРОВАНИЕ Издательско-полиграфический центр Воронежского государственного университета 2008 Утверждено научно-методическим советом геологического факультета февраля 2008 г., протокол № Рецензент проф. А.Д. Савко Авторы: С.А. »

«Владимирский государственный университет ЛАБОРАТОРНЫЕ РАБОТЫ ПО ДИСЦИПЛИНЕ ВЫСОКОМОЛЕКУЛЯРНЫЕ СОЕДИНЕНИЯ Методические указания в двух частях Часть 1 Владимир 2004 Министерство образования Российской Федерации Владимирский государственный университет Кафедра технологии переработки пластмасс ЛАБОРАТОРНЫЕ РАБОТЫ ПО ДИСЦИПЛИНЕ ВЫСОКОМОЛЕКУЛЯРНЫЕ СОЕДИНЕНИЯ Методические указания в двух частях Часть 1 Составитель Н.А. КОЗЛОВ Владимир УДК 678.64 (076.5) Рецензент Кандидат химических наук, доцент. »

«Министерство образования и науки Российской Федерации ГОУ ВПО Тамбовский государственный технический университет Рабочая тетрадь для лабораторных работ студента Ф.И.О. группа _ Подписано в печать 31.08.2009 Формат 60 84/16. 2,79 усл. печ. л. Тираж 200 экз. Заказ № 320 Издательско-полиграфический центр ТГТУ 392000, Тамбов, Советская, 106, к. 14 Тамбов Издательство ТГТУ 2009 УДК 535 ББК В343я73-5 Б907 Рецензент Доктор технических наук, профессор кафедры Автоматизированные системы и приборы ТГТУ. »

«В.А. Павлов Устройства отображения ПК Учебное пособие для вузов Рекомендовано учебно-методическим объединением вузов по университетскому политехническому образованию в качестве учебного пособия для студентов, обучающихся по специальности 220100 Вычислительные машины, комплексы, системы и сети Саров СарФТИ 2003 УДК 681.3 П12 Рецензенты: к-т техн. наук, доцент кафедры Компьютерные системы и сети МГТУ им. Н.Э. Баумана И.В. Баскаков; кафедра Вычислительная техника Нижегородского государственного. »

«МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Ухтинский государственный технический университет (УГТУ) Определение пористости горных пород Методические указания Ухта, УГТУ, 2013 УДК 552:539.217 (076.5) ББК 26.34я7 П 31 Печерин, В. Н. П 31 Определение пористости горных пород [Текст] : метод. указания / В. Н. Печерин, Н. П. Демченко. – Ухта : УГТУ, 2013. – 14 с. Методические указания предназначены для выполнения. »

«Министерство образования и науки РФ ГОУ ВПО Ярославский государственный педагогический университет им. К.Д. Ушинского В.В. Афанасьев, А.В. Муравьев, И.А. Осетров, П.В. Михайлов Спортивная метрология Учебное пособие Ярославль 2009 УДК 519.22; 796:311 Печатается по решению ББК 75 в 631.8+22.172 редакционно-издательского А 94 совета ЯГПУ им. К.Д. Ушинского Рецензенты: доктор педагогических наук, профессор М.Н. Жуков доктор физико-математических наук, профессор ЯФ РОАТ В.А. Коромыслов Афанасьев. »

«Петрозаводский государственный университет Изучение явлений дифракции лазерного излучения на простейших дифракционных структурах Методические указания к лабораторной работе ПЕТРОЗАВОДСК 1999 Рассмотрены и рекомендованы к печати на заседании редакционной комиссии по отрасли науки и техники Общая и ядерная физика 4 ноября 1998 года Печатаются по решению редакционно-издательского совета университета Составители: С.А. Чудинова, доцент, В А. Трухачева, доцент Данное издание осуществлено при. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Амурский государственный университет Кафедра Физики УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ ФИЗИКА КОНДЕНСИРОВАННОГО СОСТОЯНИЯ ВЕЩЕСТВА Основной образовательной программы по специальности 010701.65 — Физика Благовещенск 2012 1 2 СОДЕРЖАНИЕ 1. Рабочая программа учебной дисциплины 4 2. Краткое изложение программного материала 3 3 Методические. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Государственное образовательное учреждение высшего профессионального образования Амурский государственный университет (ГОУВПО АмГУ) Компьютерная графика Учебно-методический комплекс дисциплины по направлению подготовки 010600.68 – Прикладные математика и физика Утвержден на заседании кафедры теоретической и экспериментальной физики _ 20г., (протокол № от _20г. ) Зав. кафедрой Е.А. Ванина Печатается по решению редакционно-издательского совета. »

«Министерство образования Российской Федерации Ярославский государственный университет им. П. Г. Демидова А.Б. Чурилов ВВЕДЕНИЕ В НАНОЭЛЕКТРОНИКУ Учебное пособие Ярославль 2002 УДК 621.382.017.7(075.8) ББК 385я73 Ч93 Рецензенты: кафедра общей физики ЯГПУ им. К.Д. Ушинского; д–р физ.–мат. наук В.К. Смирнов Чурилов А.Б. Введение в наноэлектронику: Учеб. пос. / Яросл. гос. ун-т. Ярославль, 2002. 132 с. ISBN 5-8397-0249-8 Учебное пособие является введением в физику и технологию микроэлектроники с. »

«Федеральное агентство по здравоохранению и социальному развитию Государственное Образовательное Учреждение Высшего Профессионального Образования Амурская Государственная Медицинская Академия Б.В.Кравец МЕДИЦИНА КАТАСТРОФ учебное пособие для студентов, обучающихся по специальностям: 060101 – лечебное дело, 060103 – педиатрия, 060105 – стоматология, 060104 – медикопрофилактическое дело, 060112 – медицинская биохимия, 060113 – медицинская биофизика, 060114 – медицинская кибернетика Благовещенск. »

«КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ КАФЕДРА ФИЗИКИ ТВЕРДОГО ТЕЛА Л.Д. Зарипова ЗАЩИТА ОТ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ (методическое пособие) КАЗАНЬ 2008 УДК 530.145 БКК 22.31 И 83 Рекомендовано в печать Ученым Советом физического факультета Казанского государственного университета Рецензент: к.ф.-м.н, доцент, заведующий кабинетом изотопных методов исследований КИБ КНЦ РАН Манапов Р.А. Зарипова Л.Д. И 83 Защита от ионизирующего излучения: Учебно-методическое пособие для. »

«КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИНСТИТУТ ФИЗИКИ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ ПО АТОМНОЙ ФИЗИКЕ ГЕЛИЙ-НЕОНОВЫЙ ЛАЗЕР Казань 2012 Печатается по решению Учебно-методической комиссии Института физики КФУ УДК 539.25 Гайнутдинов Р.Х., Ильин Г.Г., Коновалова О.А., Сибгатуллин М.Э. методические указания к выполнению лабораторной работы по атомной физике Гелий-неоновый лазер, Казань, 2012, 60 с. Данное пособие написано для студентов 3 курса физического. »

© 2013 www.diss.seluk.ru — «Бесплатная электронная библиотека — Авторефераты, Диссертации, Монографии, Методички, учебные программы»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.