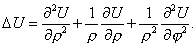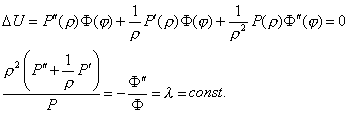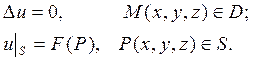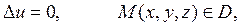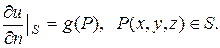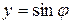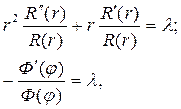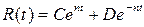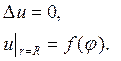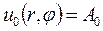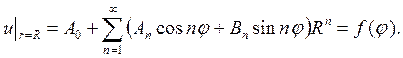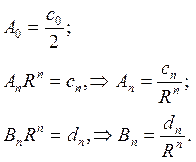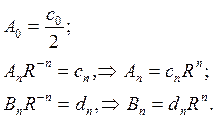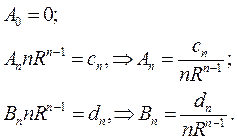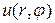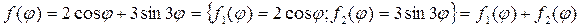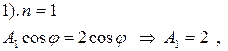Краевые задачи для уравнения лапласа в круговом цилиндре
Краевые задачи для уравнения лапласа в круговом цилиндре
Настоящая книга является естественным дополнением пособия А. Г. Свешникова, А. Н. Боголюбова, В. В. Кравцова «Лекции по математической физике». Её основная цель помочь студентам приобрести необходимые практические навыки исследования математических моделей физических явлений, являющихся краевыми или начально-краевыми задачами для линейных дифференциальных уравнений в частных производных второго порядка. С этой целью каждая глава пособия построена следующим образом. В начале каждого параграфа главы приводятся необходимые минимальные сведения теоретического характера, используемые для решения данного типа задач. Затем эти методы демонстрируются в работе, для чего даются примеры решения конкретных задач. В конце главы приводятся задачи с ответами для самостоятельного решения.
Содержание пособия полностью соответствует курсу «Методы математической физики», читаемому на физическом факультете МГУ. Пособие написано на основе более чем двадцатилетнего опыта преподавания на физическом факультете Московского университета. Оно рассчитано в первую очередь на студентов физических специальностей университетов, но будет полезно и студентам инженерных специальностей и лицам, занимающимся математической физикой и прикладной математикой.
Авторы выражают свою глубокую благодарность заведующему кафедрой Московского государственного института электронной профессору А. С. Поспелову, профессорам А. В. Ефимову, А. С. Ильинскому и С. Я. Секерж-Зеньковичу, взявшим на себя труд ознакомиться с рукописью и сделавшим ряд ценных замечаний.
Краевые задачи для уравнения лапласа в круговом цилиндре
3.3. Задача Дирихле для уравнения Лапласа в кольце
Найти функцию U, удовлетворяющую уравнению
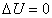 внутри кольца. внутри кольца. | (1) |
Необходимо поставить краевые условия на каждой из границ:
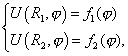 | (2) |
где 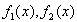

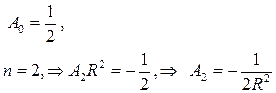
Для простоты вычислений возьмем 
тогда краевые условия примут вид
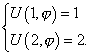 | (2*) |
Запишем уравнение (1) в полярных координатах
Решим уравнение методом разделения переменных, то есть будем искать решение уравнения (1) вида
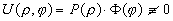
Тогда уравнение (1) примет вид
Отсюда получим два обыкновенных дифференциальных уравнения.
  |
Необходимо определить знак 

и при 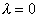
Удовлетворим краевым условиям (2*). Необходимо выяснить, какие из коэффициентов являются лишними.
Решения краевых задач для уравнения Лапласа в круге


Уравнением Лапласа описываются различные физические процессы и в каждой задаче искомое решение должно удовлетворять уравнению в некоторой области D, а также некоторому дополнительному условию на границе S этой области D.
В зависимости от вида граничного условия различают следующие основные виды граничных задач:
1) найти решение уравнения Лапласа, удовлетворяющее граничным условиям первого рода: 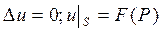
2) найти решение уравнения Лапласа, удовлетворяющее граничным условиям второго рода: 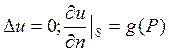
3) найти решение уравнения Лапласа, удовлетворяющее граничным условиям третьего рода: 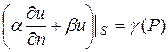
где 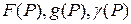
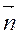
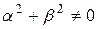
Краевые задачи могут быть внутренними или внешними. Они различаются в зависимости от того, в какой области внутренней или внешней относительно поверхности S ищется решение.
Внутренняя задача Дирихле формулируется следующим образом: Найти непрерывную в замкнутой области 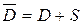
Внутренняя задача Неймана формулируется так: найти внутри области D решение и(М) уравнения Лапласа
непрерывное в замкнутой области 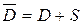
Рассмотрим теперь краевые задачи для уравнения Лапласа внутри круга и вне его. Пусть существует область, представляющая собой круг радиуса R. Запишем двухмерное уравнение Лапласа в полярных координатах, полагая, что 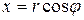
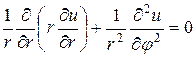
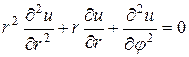
Для нахождения частных решений уравнения (18.12) используем метод Фурье и представим эти решения в виде
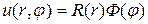
После подстановки решения (18,13), первой и второй производной от этой функции по r, а также второй производной от нее по φ в исходное уравнение (18.12), получим
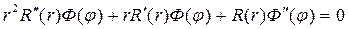
Разделим в этом уравнении переменные
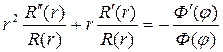
Это равенство выполняется тогда и только тогда, если обе его части равны одной и той же постоянной, например, λ
Тогда для каждой функции 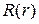
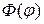
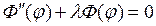
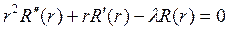
Рассмотрим сначала уравнение (18.15) для функции 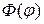
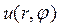
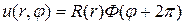
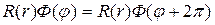
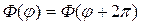
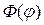
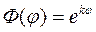
После подстановки которого в уравнение (18.15) получим характеристическое уравнение
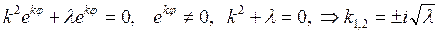
Корни характеристического уравнения являются исключительно мнимыми, поэтому общее решение уравнения (18.15) при 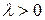
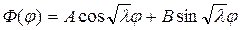
и в силу периодичности функции 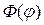
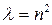
В самом деле, из равенства
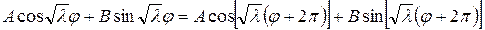
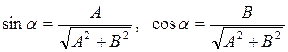
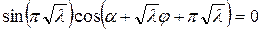
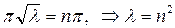
Следовательно, частные решения уравнения (18.15) при различных значениях n можно записать в виде
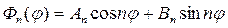
Исходя из (18.18) следует, что уравнение (18.16) можно записать в виде
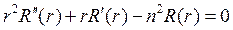
Уравнение (18.20) в случае, когда 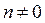
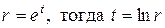
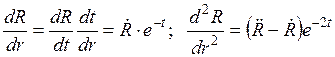
Следовательно, подставив эти производные в уравнение (18.19) получим обыкновенное линейное и однородное дифференциальное уравнение с постоянными коэффициентами
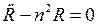
Решение этого уравнения будем искать в виде
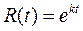
Вычислим от этой функции производные и подставим в уравнение (18.21)
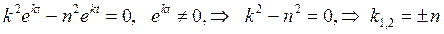
следовательно общее решение уравнения (18.21) имеет вид
и возвращаясь к переменной r, получим
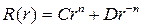
Если в уравнении (18.20) 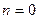
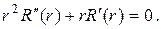
Это уравнение также является уравнением Эйлера, поэтому, производя замену 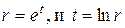
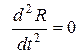
решение которого будет иметь вид
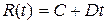
и возвращаясь к переменной r, получим
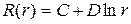
решение уравнения (18.20) при 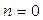
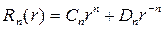
Подставляя (18.19) и (18.25) в решение (18.13) получим набор частных решений
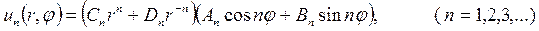
используя принцип суперпозиции, а также вследствие линейности и однородности уравнения Лапласа можно утверждать, что сумма частных решений также будет его решением, следовательно, общее решение уравнения Лапласа будет иметь вид
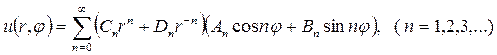
Пользуясь этой формулой и задавая граничные условия первого, второго и третьего рода можно решать как внутренние, таки внешние граничные задачи – Дирихле, Неймана и смешанную задачу.
I.Рассмотрим внутреннюю задачу Дирихле для уравнения Лапласа в круге радиуса R
Для решения этой задачи используем формулу (18.26), учитывая при этом, что функция 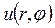
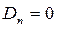
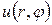
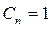
получим решение уравнения Лапласа
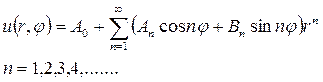
Удовлетворим в этом решении поставленным граничным условиям
Разложим функцию f(φ) в ряд Фурье на интервале от 0 до 2π
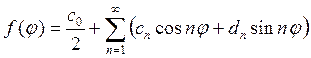
следовательно, можно записать
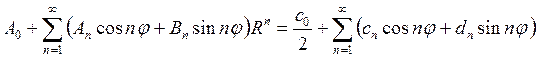
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства
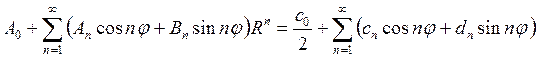
найдем значения искомых коэффициентов An и Bn
Подставляя найденные коэффициенты в решение (18.27), получим окончательное решение внутренней задачи Дирихле для уравнения Лапласа в круге
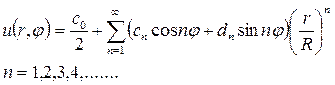
где cn и dn коэффициенты, заданные поставленными граничными условиями.
Решение задачи Дирихле также можно получить и используя формулу Пуассона
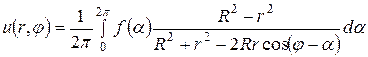
которая при непрерывной функции 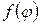
II.Рассмотрим внешнюю задачу Дирихле для уравнения Лапласа в круге радиуса R
Для решения этой задачи используем формулу (18.26), учитывая при этом, что функция 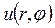
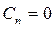
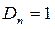
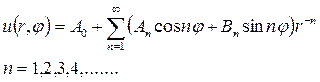
Удовлетворим в этом решении поставленным граничным условиям
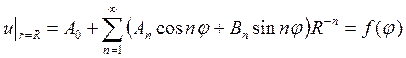
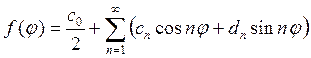
Следовательно, можно записать
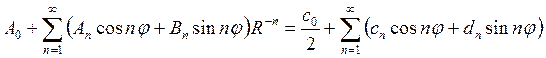
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства
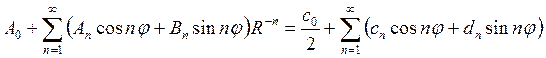
найдем значения искомых коэффициентов An и Bn
Подставляя найденные коэффициенты в решение (18.30), получим окончательное решение внутренней задачи Дирихле для уравнения Лапласа в круге
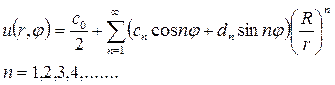
где cn и dn коэффициенты, заданные поставленными граничными условиями.
III.Рассмотрим внутреннюю задачу Неймана:
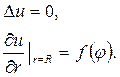
Для решения этой задачи вычислим производную от решения (18.27)
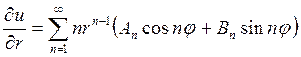
И запишем граничные условия
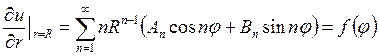
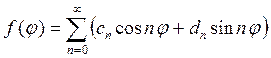
Следовательно, можно записать
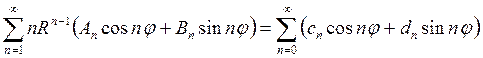
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства, найдем значения искомых коэффициентов An и Bn
Подставляя найденные коэффициенты в решение (18.33), получим окончательное решение внутренней задачи Неймана для уравнения Лапласа в круге
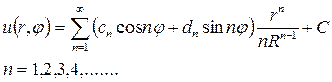
где С – произвольная постоянная.
Необходимо отметить, что решение задачи Неймана существует только при условии
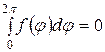
и определяется с точностью до произвольной постоянной.
Смешанная граничная задача для уравнения Лапласа в круге радиуса R решается аналогично задачам рассмотренным выше.
Пример 18.1. Найти решение уравнения Лапласа для внутренней части круга радиуса R, удовлетворяющее краевому условию
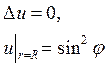
▲ Здесь задана задача Дирихле, где правая часть граничного условия (П18.1.1) 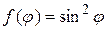
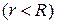
Для этого подставим само решение (18.28) в левую часть граничного условия (П18.1.1) при 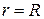
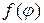
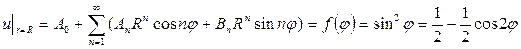
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами и при свободном члене в левой и правой частях полученного равенства (П18.1.2)
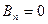
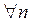
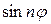
а также все остальные 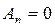
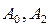
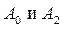
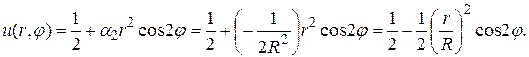
Пример 18.2. Найти решение уравнения Лапласа внутри круга радиуса R 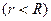
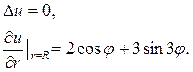
▲ Здесь задана задача Неймана, где правая часть граничного условия (П18.2.1) 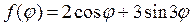
и для каждой из них найдем решение. Прежде чем решать поставленную задачу проверим выполнение условия (18.32)
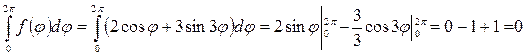
так как условие (18.32) выполнено, то для решения поставленной задачи воспользуемся, описанном выше алгоритмом (III.)
Вычислим производную от решения (18.27)
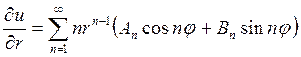
и запишем граничные условия сначала для функции
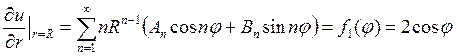
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами в левой и правой частях полученного равенства (П18.2.2):
а все остальные 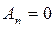
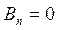
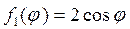
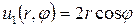
Затем запишем граничные условия сначала для функции
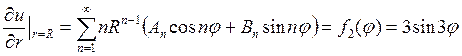
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами в левой и правой частях полученного равенства (П18.2.3):
а все остальные 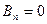
Следовательно, решение, соответствующее функции 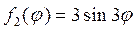
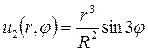
Таким образом, решение исходной задачи будет определяться формулой
Численные методы решения краевых задач
Постановка задачи и основные положения
Рассмотрим двухточечные краевые задачи, часто встречающиеся в приложениях, например, при решении задач вариационного исчисления, оптимального управления, механики жидкости и газа и др. Пусть дано обыкновенное дифференциальное уравнение
и краевые условия
где [math]F \bigl(x,y,y’,\ldots,y^<(n)>\bigr);
j=\overline
Если уравнения (7.1),(7.2) линейны относительно искомой функции и ее производных, то краевая задача называется линейной.
Для простоты ограничимся частным случаем линейной краевой задачи для дифференциального уравнения второго порядка [math](n=2)[/math] , которая наиболее часто ставится в вычислительной практике и записывается в виде
(\Omega \equiv [a,b]),[/math]
где [math]p(x),\, q(x),\, f(x)\in C_2[a,b][/math] — заданные функции, а [math]\alpha_0,\,\alpha_1,\, \beta_0,\, \beta_1,\,A,\,B[/math] — заданные числа, 0,
j=0;1[/math] . Требуется найти функцию [math]y(x)[/math] , удовлетворяющую уравнению (7.3) и краевым условиям (7.4). Краевые условия при [math]\alpha_
j=0;1[/math] , задают линейную связь между значениями искомого решения и его производной на концах отрезка [math][a,b][/math] .
В простейшем случае, когда [math]\beta_0=0,
\beta_1=0[/math] , краевые условия задают на концах отрезка [math][a,b][/math] только значения функции [math]y(a),\,y(b)[/math] . Такие функциональные условия называют краевыми условиями первого рода. В этом случае краевая задача называется первой краевой задачей.
В случае, когда [math]\alpha_0=0,
\alpha_1=0[/math] , т.е. на концах отрезка заданы только значения производных, краевые условия являются дифференциальными. Такие краевые условия называют условиями второго рода или «мягкими». Последнее название обусловлено тем, что они определяют на концах отрезка [math][a,b][/math] всего лишь наклоны интегральных кривых, а не значения функции [math]y(x)[/math] . В этом случае задача (7.3),(7.4) называется второй краевой задачей.
В общем случае, когда [math]\alpha_0[/math] и (или) [math]\alpha_1;
\beta_0[/math] и (или) [math]\beta_1[/math] не равны нулю, краевые условия носят функционально-дифференциальный характер и называются условиями третьего рода. Тогда задача (7.3),(7.4) называется третьей краевой задачей.
Например, условия [math]y(a)=A,
y(b)=B[/math] являются условиями первого рода. Геометрически это означает, что при решении первой краевой задачи требуется найти интегральную кривую уравнения (7.3), проходящую через данные точки [math](a,A),\, (b,B)[/math] (рис. 7.1,а). Условия [math]y'(a)=A,\, y'(b)=B[/math] являются условиями второго рода. Геометрически вторая краевая задача сводится к отысканию интегральной кривой уравнения, пересекающей прямые [math]x=a,
x=b[/math] под заданными углами [math]\alpha,\,\beta[/math] , где [math]\operatorname
\operatorname
y(b)=B[/math] являются частным случаем краевых условий третьего рода, так как [math]\alpha_0=0,
\beta_1=0[/math] . Геометрически данная краевая задача сводится к отысканию интегральной кривой уравнения, проходящей через точку [math](b,B)[/math] и пересекающей прямую [math]x=a[/math] под данным углом [math]\alpha[/math] , где [math]\operatorname
В общем случае краевая задача может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь несколько или бесконечно много решений.
Утверждение 7.1 (о существовании и единственности решения краевой задачи (7.3),(7.4)). Для того чтобы существовало единственное решение краевой задачи (7.3),(7.4), необходимо и достаточно, чтобы однородная краевая задача
имела только тривиальное решение [math]y(x)\equiv0[/math] .
Пример 7.1. Найти аналитическое решение следующих краевых задач:
0 \leqslant x \leqslant \frac<\pi><2>,
y\! \left(\frac<\pi><2>\right)-y’\! \left(\frac<\pi><2>\right)=2[/math] (третья краевая задача);
0 \leqslant x \leqslant 1,
y(1)=0[/math] (первая краевая задача).
Воспользуемся известной методикой отыскания общих решений дифференциальных уравнений. Подставив в них заданные краевые условия, получим аналитические решения данных краевых задач.
1. Найдем общее решение однородного уравнения [math]y»+y=0[/math] , одинакового для обеих рассматриваемых задач. Так как характеристическое уравнение [math]\lambda^2+1=0[/math] имеет комплексные сопряженные корни [math]\lambda_<1,2>=\pm i= \alpha\pm \beta i[/math] [math](\alpha=0,
\beta=1)[/math] , то общее решение будет
2. Частные решения неоднородных уравнений находятся методом подбора. Подставляя [math]y_<\text
D=-1[/math] . Поэтому [math]y_<\text
3. Найдем общее решение неоднородного уравнения как сумму общего решения однородного уравнения и частного решения неоднородного уравнения:
а) [math]y(x)=C_1\cos x+C_2\sin x+1[/math] ; б) [math]y(x)=C_1\cos x+C_2\sin x-x[/math] .
4. Определим значения произвольных постоянных из краевых условий третьего рода (случай «а») и первого рода (случай «б»):
а) найдем [math]y'(x)=-C_1\sin x+C_2\cos x[/math] . Тогда
Отсюда [math]C_1=1[/math] и [math]y(x)=1+\cos x[/math] — решение краевой задачи «а»;
б) общее решение [math]y(x)=C_1\cos x+C_2\sin x-x[/math] и, следовательно, [math]y(0)=C_1=0,
y(1)=C_1\cos1+ C_2\sin1-1=0[/math] , отсюда [math]C_2= \frac<1><\sin1>[/math] и [math]y(x)=\frac<\sin x><\sin1>-x[/math] — решение краевой задачи «б». Таким образом, решение краевой задачи представляет собой такое частное решение, которое удовлетворяет краевым условиям.
Рассмотренный метод нахождения аналитического решения краевых задач применим для ограниченного класса задач. Поэтому в вычислительной практике используются численные и приближенно-аналитические методы, позволяющие найти приближенное решение краевых задач, точные аналитические решения которых не могут быть найдены.
Метод сеток
Рассмотрим линейную краевую задачу с краевыми условиями первого рода (первую краевую задачу):
где [math]p(x),q(x),f(x)\in C_2[a,b][/math] — заданные функции; [math]A,\,B[/math] — заданные числа.
Очевидно, любой отрезок [math][a,b][/math] , на котором ищется решение краевой задачи, можно привести к отрезку [math][0;1][/math] с помощью линейного преобразования [math]\widetilde
Утверждение 7.2 (о единственности решения краевой задачи (7.5)). Если функции [math]p(x),q(x),f(x)[/math] принадлежат классу [math]C_2[a,b],
q(x) \geqslant 0[/math] на [math][0;1][/math] , то краевая задача (7.5) имеет единственное решение [math]y(x)\in C_4[0;1][/math] .
Для решения задачи (7.5) применим метод сеток, получаемый путем аппроксимации первой и второй производных. Введем равномерную сетку (где [math]n[/math] — число отрезков разбиения)
Функции [math]p(x),q(x),f(x)[/math] заменяются их проекциями на сетку [math]\Omega_n[/math] , то есть [math]p(x)\to p(x_)=p_i,[/math] [math]q(x)\to q(x_)=q_i,[/math] [math]f(x)\to f(x_)= f_i,[/math] . Вместо точного решения [math]y(x)[/math] отыскивается некоторое приближение [math]\widehat
i=\overline<0,n>[/math] . Первая и вторая производные аппроксимируются на трехточечном шаблоне [math](x_
Краевые условия для этой задачи аппроксимируются точно, т.е. [math]y(a)[/math] и [math]y(b)[/math] заменяются на [math]\widehat
представляющей собой систему алгебраических уравнений трехдиагонального вида:
\delta_=f_[/math] . Здесь система (7.6) записана для внутренних узлов сетки [math]\Omega_n[/math] . Она является трехдиагональной системой линейных алгебраических уравнений и решается методом прогонки.
1. Изложенный метод сеток допускает обобщение. Например, его можно применять для решения нелинейной краевой задачи:
где [math]F(x,y)[/math] — нелинейная по [math]y[/math] функция (в общем случае, который здесь не рассматривается, функция [math]F[/math] зависит также и от [math]y'[/math] ).
Рассуждая аналогично рассмотренному выше способу, перейдем к разностной задаче:
В силу нелинейности правой части полученная алгебраическая система является нелинейной и для ее решения нельзя использовать метод прогонки в том виде, в каком он изложен для линейной задачи. Поэтому для ее решения используем метод простых итераций, с помощью которого при фиксированном [math]k[/math] (номер итерации) система алгебраических уравнений (7.8) превращается в линейную, так как величины, входящие в правую часть системы, известны из предыдущей итерации. Действительно, для k-й итерации получается система (которая решается на каждой итерации методом прогонки)
Можно показать, что итерации сходятся при выполнении условия [math]q=\frac<1><8>(x_n-x_0)^2M_1 [math]M_1=\max_<[a,b]>\left|\frac<\partial F><\partial y>\right|[/math] с линейной скоростью.
2. Краевые условия второго и третьего рода в задаче, аналогичной (7.5), могут быть аппроксимированы несколькими способами.
Первый способ. Использование аппроксимационных формул (5.4) первого порядка
В силу первого порядка этих аппроксимаций метод сеток в этом случае также будет иметь первый порядок аппроксимации.
Второй способ. Применение формулы Тейлора и ее преобразование с использованием дифференциального уравнения. Таким способом может быть достигнут второй порядок аппроксимации.
Третий способ. Применение левосторонней (5.8) и правосторонней (5.9) формул, аппроксимирующих производные со вторым порядком:
3. Порядок аппроксимации схемы определяется минимальным порядком аппроксимации дифференциального уравнения и краевых условий.
Алгоритм применения метода сеток
1. Задать сетку [math]\Omega_n[/math] на отрезке [math][a,b][/math] или сформировать ее из условий достижения требуемой точности.
2. Используя аппроксимационные формулы (5.10),(5.14) и один из трех способов аппроксимации краевых условий (в случае, если они второго или третьего рода), перейти от исходной дифференциальной задачи к системе алгебраических уравнений (разностной схеме), неизвестными в которой являются величины, «близкие» к решению краевой задачи в узлах сетки.
3. Найти решение разностной задачи путем решения трехдиагональной системы уравнений и таким образом определить приближенное решение краевой задачи.
Пример 7.2. Найти приближенное решение краевой задачи [math]y»+y=1,
0 \leqslant x \leqslant \frac<\pi><2>,[/math] [math]y'(0)=0,[/math] [math]y\! \left(\frac<\pi><2>\right)-y’\! \left(\frac<\pi><2>\right)=2[/math] при [math]n=3[/math] , используя первый способ аппроксимации краевых условий. Записать разностные схемы для второго и третьего способов при произвольном [math]n[/math] .
В поставленной задаче
Для решения задачи воспользуемся методикой.
1. Так как [math]n=3[/math] , то сетка имеет вид [math]\Omega_3=\
y\! \left(\frac<\pi><6>\right)=y_1,[/math] [math]y\! \left(\frac<\pi><3>\right)=y_2,[/math] [math]y\! \left(\frac<\pi><2>\right)=y_3[/math] . Будем искать приближенные значения [math]\widehat
2. Составим разностную схему. Согласно (7.6), для внутренних узлов сетки получаем
i=1;2[/math] или [math]\widehat
Применим первый способ аппроксимации краевых условий. По формуле (5.4) с учетом условия [math]y'(0)=0[/math] на левом конце имеем
На правом конце [math]y\! \left(\frac<\pi><2>\right)=y_3,
y’\! \left(\frac<\pi><2>\right)=y’_3[/math] , и по второй из формул (7.9) [math]\widehat
В результате получаем разностную схему первого порядка аппроксимации (трехдиагональную систему линейных алгебраических уравнений)
Сравнивая первое уравнение этой системы с рекуррентным соотношением [math]\widehat
После этого вычисляются все последующие прогоночные коэффициенты по формулам:
Здесь [math]\alpha_,\beta_,\gamma_[/math] соответствуют коэффициентам левой части полученной алгебраической системы, а [math]\delta_[/math] — правой части.
Далее выполняется обратный ход: [math]\widehat
\widehat
\widehat
Результаты решения краевой задачи приведены в табл. 7.1, в которой последний столбец соответствует точному решению [math]y(x)=1+\cos x[/math] , найденному в примере 7.1.
7.1>>\\\hline i& \alpha_& \beta_& \gamma_& \delta_& P_& Q_& \widehat
В силу того, что краевые условия аппроксимированы с первым порядком относительно [math]h[/math] , в данном случае получена разностная схема первого порядка, так как порядок аппроксимации схемы определяется минимальным порядком аппроксимации дифференциального уравнения и краевых условий.
Воспользуемся вторым способом аппроксимации краевых условий для построения разностной схемы второго порядка аппроксимации. Разложим [math]y(x)[/math] в точке [math]x=x_1[/math] относительно точки [math]x_0[/math] по формуле Тейлора:
Выразим из этого соотношения [math]y'(x_0)[/math] и подставим в него вместо [math]y»(x_0)[/math] выражение [math]y»(x_0)=1-y(x_0)=1-y_0[/math] , определяемое исходным дифференциальным уравнением:
Как показывает это соотношение, дифференциальное условие на левой границе аппроксимируется на двухточечном шаблоне [math](x_0,x_1)[/math] со вторым порядком аппроксимации двухточечным алгебраическим уравнением:
Аналогично получается двухточечное алгебраическое уравнение при / [math]i=n-1[/math] и [math]i=n[/math] . Разложение [math]y(x)[/math] в точке [math]x=x_
Выражая отсюда [math]y'(x_n)[/math] с учетом связи [math]y»(x_n)=1-y(x_n)=1-y_n[/math] , следующей из исходного дифференциального уравнения, получаем
Подставим это выражение в граничное условие:
Таким образом, система линейных алгебраических уравнений в окончательном виде записывается следующим образом:
Эта трехдиагональная система, отличающаяся от полученной первым способом только первым и последним уравнениями, решается численно методом прогонки.
Применим третий способ аппроксимации краевых условий для построения разностной схемы второго порядка. Так, для крайней левой точки используется левосторонняя формула (5.8):
Тогда получается трехточечное алгебраическое уравнение:
Аппроксимация производной [math]y’\! \left(\frac<\pi><2>\right)[/math] в крайней правой точке по правосторонней формуле [math]\widehat
Тогда в этом случае получается следующая система линейных алгебраических уравнений:
Здесь [math]\widehat
Методы минимизации невязки
Описываемые здесь методы относятся к приближенно-аналитическим и могут применяться при решении достаточно широкого класса задач. На основе одного из приближенно-аналитических методов (метода Галеркина) строится метод конечных элементов, излагаемый в разд. 7.5.
Рассмотрим линейную краевую задачу (7.3),(7.4). Ее решение будем искать в виде
где [math]\varphi_0(x), \varphi_1(x), \ldots, \varphi_m(x)[/math] — элементы заданной системы функций; [math]a_1,\ldots,a_m[/math] — неопределенные коэффициенты. Заданная система функций называется базисной, и ее элементы должны удовлетворять условиям:
а) [math]\varphi_
б) при любом конечном [math]m[/math] функции [math]\varphi_1(x), \ldots, \varphi_m(x)[/math] линейно независимы на отрезке [math][a,b][/math] ;
в) [math]\varphi_0(x)[/math] удовлетворяет краевым условиям (7.4)
г) [math]\varphi_1(x), \ldots, \varphi_m(x)[/math] удовлетворяют условиям
называется невязкой . Она равна разности левой и правой частей уравнения (7.3), образующейся при подстановке [math]\widehat
то функция [math]\widehat
Однако при решении краевых задач, как правило, не удается получить невязку тождественно равной нулю. Поэтому ставится задача: вычислить коэффициенты [math]a_1,\ldots,a_m[/math] таким образом, чтобы невязка в каком-либо смысле стала меньшей. Полученные в результате коэффициенты определяют приближенное решение (7.11).
Выражение для невязки [math]\varepsilon(x; a_1,\ldots, a_m)[/math] с учетом (7.11) удобно записывать в следующей эквивалентной форме:
где [math]L\widehat
L[/math] — линейный оператор задачи (7.3),(7.4) (выполняются равенства [math]L(y+z)= Ly+Lz,[/math] [math]L(Cy)=C\cdot Ly[/math] для любых [math]y,\,z[/math] и постоянной [math]C[/math] ).
Рассмотрим различные методы, минимизирующие невязку .
А. Метод коллокации. На интервале [math](a,b)[/math] задаются т точек [math]x_1,\ldots, x_n[/math] (точек коллокации) и требуется, чтобы в каждой из них невязка (7.14) обращалась в нуль:
С учетом (7.16) эта система принимает вид
Если полученная система [math]m[/math] линейных уравнений совместна, то из нее определяются коэффициенты [math]a_1,\ldots, a_m[/math] , которые затем подставляются в (7.11).
Б. Метод наименьших квадратов (непрерывный вариант). Неизвестные коэффициенты [math]a_1,\ldots, a_m[/math] должны обеспечивать минимум интеграла от квадрата невязки:
Для решения задачи применяются необходимые условия безусловного экстремум:
Подставляя (7.16) в (7.19), получаем систему [math]m[/math] линейных алгебраических уравнений для нахождения коэффициентов [math]a_1,\ldots, a_m\colon[/math]
В. Метод наименьших квадратов (дискретный вариант). Неизвестные коэффициенты [math]a_1,\ldots,a_m[/math] должны обеспечивать минимум суммы квадратов значений невязки в заданном наборе точек [math]x_1,\ldots,x_n;
n \geqslant m[/math] , то есть [math]x_\in (a,b),
Для решения задачи применяются необходимые условия безусловного экстремума
Отсюда следует система [math]m[/math] линейных уравнений для нахождения коэффициентов [math]a_1,\ldots,a_m[/math] , которая по форме записи совпадает с (7.20), но скалярное произведение определяется по формуле [math]\textstyle<(f,g)= \sum\limits_
Замечание. При [math]n=m[/math] результаты, полученные точечным методом наименьших квадратов и методом коллокации, совпадают. В этом случае точки [math]x_1,\ldots, x_n[/math] являются точками коллокации.
Г. Метод моментов (взвешенных невязок). Неизвестные коэффициенты ах. ат находятся из условия равенства нулю /и моментов невязки:
j=\overline<1,m>[/math] — функции, удовлетворяющие условиям:
б) функции [math]\psi_
j=\overline<1,m>[/math] называются весовыми, а условие (7.22) является условием ортогональности невязки к весовым функциям.
Д. Метод Галсркина. Он является частным случаем метода моментов, когда в качестве весовых функций используются базисные. Коэффициенты [math]a_1,\ldots,a_m[/math] находятся из условия ортогональности функций базисной системы [math]\varphi_1(x),\ldots, \varphi_
Отсюда следует система [math]m[/math] линейных уравнений для нахождения коэффициентов:
Известно, что при достаточно большом [math]m[/math] условие (7.23) обеспечивает малость невязки в среднем.
Алгоритм применения методов минимизации невязки
1. В выражении (7.11) выбрать систему базисных функций, задать число [math]m[/math] в зависимости от требуемой точности.
2. Найти коэффициенты [math]a_1,\ldots,a_m[/math] путем решения одной из систем алгебраических уравнений (7.18),(7.20),(7.24) в зависимости от выбранного метода.
3. Выписать приближенное решение краевой задачи по формуле (7.11).
Пример 7.3. Найти приближенное решение краевой задачи [math]y»+y=-x,
0 \leqslant x \leqslant 1,[/math] [math]y(0)=0,
y(1)=0[/math] методом коллокации, интегральным методом наименьших квадратов, методом Галеркина
В поставленной задаче
Точное решение найдено в примере 7.1.
Воспользуемся сначала методом коллокации.
1. Зададим [math]m=2[/math] и будем искать решение в виде
где [math]\varphi_0(x)\equiv0[/math] (эта функция удовлетворяет каждому из краевых условий, т.е. [math]\varphi_0(0)=0,
\varphi_0(1)=0[/math] ), функции [math]\varphi_1(x)= x(1-x),
\varphi_2(x)= x^2(1-x)[/math] . Функции [math]\varphi_1(x),\, \varphi_2(x)[/math] линейно независимые, дважды непрерывно дифференцируемые и удовлетворяют условию (7.13). Действительно,
Таким образом, решение краевой задачи ищется в форме
2. Так как [math]m=2[/math] и [math]\varphi_0(x)\equiv 0[/math] , то система (7.18) имеет вид
Выберем узлы коллокации: [math]x_1=1\!\!\not<\phantom<|>>\,4,
Таким образом, имеем линейную систему относительно [math]a_1[/math] и [math]a_2\colon[/math]
3. Приближенное решение задачи: [math]\widehat
Решим теперь задачу методом наименьших квадратов (см. непрерывный вариант).
1. Решение краевой задачи ищется в форме [math]\widehat
2. Так как [math]f(x)=-x,
\varphi_0(x)\equiv 0[/math] , то система (7.20) имеет вид
Итак, имеем линейную систему относительно [math]a_1[/math] и [math]a_2\colon[/math]
Приближенное решение задачи: [math]\widehat
Решим задачу методом Галеркина.
1. Пусть сначала [math]m=1[/math] . Решение ищется в форме [math]\widehat
2. Тогда система (7.24) преобразуется к виду
Так как [math]\varphi_1(x)= x(1-x),
L\varphi_1(x)= \varphi»_1(x)+ \varphi_1(x)=-2+x(1-x)[/math] , получаем
После вычисления интегралов имеем уравнение [math]-\frac<3><10>\,a_1=-\frac<1><12>[/math] , откуда [math]a_1=\frac<5><18>[/math] .
3. Приближенное решение краевой задачи: [math]\widehat
1. Решение краевой задачи ищется в форме [math]\widehat
2. Тогда система (7.24) имеет вид
Вычисляя интегралы, находим
3. Приближенное решение краевой задачи: [math]\widehat
Сопоставим полученные решения с точным (табл. 7.2).
7.2>>\\\hline x& y_<\text
Очевидно, метод Галеркина дал более точный результат.
Пример 7.4. Найти приближенное решение краевой задачи [math]y»+2xy’-2y=2x^2,
0 \leqslant x \leqslant 1,[/math] [math]y'(0)=-2,
y(1)+y'(1)=0[/math] методом Галеркина.
В поставленной задаче
1. Зададим [math]m=2[/math] и подберем функции [math]\varphi_0(x),\, \varphi_1(x),\, \varphi_2(x)[/math] , используя систему [math]1,x,x^2,\ldots[/math] . Функция [math]\varphi_0(x)[/math] должна удовлетворять условиям (7.12):
Пусть [math]\varphi_0(x)=b+cx[/math] , где [math]b,\,c[/math] — неопределенные коэффициенты. Тогда
Отсюда [math]b=4[/math] и [math]\varphi_0(x)=4-2x[/math] .
Функции [math]\varphi_1(x),\, \varphi_2(x)[/math] должны удовлетворять условиям (7.13):
Первое условие выполняется для функций вида [math]\varphi_
Таким образом, решение краевой задачи ищется в форме
2. Тогда система (7.24) имеет вид
3. Приближенное решение краевой задачи [math]\widehat
Методы сведения краевой задачи к задаче Коши
Метод стрельбы. Суть этого метода заключается в сведении решения краевой задачи к многократному решению задачи Коши. Принцип построения метода стрельбы рассмотрим на примере нелинейной краевой задачи:
где [math]f(x,y,y’)[/math] — нелинейная функция, обусловливающая нелинейность дифференциального уравнения (7.25).
При введении новой переменой [math]z=y'[/math] уравнение (7.25) записывается в нормальной форме Коши, а краевые условия видоизменяются:
где [math]\eta=y'(a)=\operatorname
Следовательно, требуется найти такое значение параметра [math]\eta[/math] , чтобы оно было корнем нелинейного уравнения [math]\Phi(\eta)= y(b,n)-B=0[/math] . Для решения этого уравнения, как правило, используются методы половинного деления или секущих. В случае использования метода половинного деления сначала делают «пробные» выстрелы при выбранных наугад или в соответствии с некоторым алгоритмом значениях [math]\eta[/math] до тех пор, пока среди значений [math]\Phi(\eta)[/math] не окажется двух противоположных по знаку. Им соответствует начальный интервал неопределенности, который далее последовательно сокращается путем деления пополам. При применении метода секущих используется формула
где [math]\eta^<(0)>,\,\eta^<(1)>[/math] — начальные значения параметра, [math]k[/math] — номер итерации. Итерации прекращаются при выполнении условия окончания [math]\bigl|\Phi(\eta^<(k)>)\bigr| \leqslant \varepsilon[/math] или [math]\bigl|\eta^<(k+1)>-\eta^<(k)>\bigr| \leqslant \varepsilon[/math] с некоторым положительным [math]\varepsilon[/math] , характеризующим точность решения задачи.
Замечание. Точность решения краевой задачи зависит не только от точности определения параметра [math]\eta[/math] , но также и от точности решения соответствующей задачи Коши. Поэтому одновременно с уточнением параметра [math]\eta[/math] рекомендуется уменьшать шаг при решении задачи Коши, либо выбирать более точный метод.
Рассмотрим применение метода стрельбы для решения линейной краевой задачи (7.3),(7.4):
Краевые задачи для уравнения Лапласа
Автор работы: Пользователь скрыл имя, 17 Ноября 2011 в 18:30, курсовая работа
Краткое описание
Рассмотрение понятия краевой задачи для уравнений эллиптического типа. Как частный случай — уравнение Лапласа (простейшее уравнение эллиптического типа). Для уравнения Лапласа краевая задача I рода — задача Дирихле; краевая задача II рода — задача Неймана. Краевое условие III рода — смешанная краевая задача. Рассматриваются также задача Дирихле в пространств/на плоскости, решение задачи Дирихле (первой краевой задачи) для уравнения Лапласа в круге, решение задачи Неймана (второй краевой задачи) для уравнения Лапласа в круге, решение задачи Дирихле для кольца.
Содержание
Введение
Понятие краевой задачи для обыкновенного дифференциального уравнения. Краевые задачи для уравнений эллиптического типа
Уравнение Лапласа и понятие гармонической функции.
Корректность краевой задачи.
Первая и вторая краевые задачи для уравнения Лапласа.
Задача Дирихле в пространстве
Задача Дирихле на плоскости
Задача Неймана
Уравнение Лапласа в цилиндрических координатах.
Решение задачи Дирихле (первой краевой задачи) для уравнения Лапласа в круге.
Решение задачи Неймана для уравнения Лапласа в круге.
Примеры.
Решение задачи Дирихле для кольца.
Вложенные файлы: 1 файл
Понятие краевой з.doc
Вещественнозначная функция класса называется гармонической в области , если она удовлетворяет уравнению Лапласа в этой области.
При гармонические функции сводятся к линейным функциям и потому их теория интереса не представляет. Поэтому в дальнейшем будем считать .
Рассмотрим некоторую замкнутую поверхность , не обязательно связную, и пусть ограничивает область , конечную или бесконечную. В обоих случаях предполагается, что сама поверхность конечна. Будем изучать поведение решений однородного уравнения Лапласа в подобных областях.
Функция называется гармонической в конечной области , если она в обладает непрерывными частными производными до второго порядка включительно (т.е. дважды непрерывно дифференцируема) и удовлетворяет однородному уравнению Лапласа.
Будем говорить, что функция гармоническая в бесконечной области, если в каждой точке этой области, находящейся на конечном расстоянии от начала, дважды
непрерывно дифференцируема, удовлетворяет однородному уравнению Лапласа и на бесконечности имеет порядок, такой что для достаточно больших имеет место неравенство ,
где размерность пространства, а некоторая постоянная. В случае двумерной области ( = 2) условие означает, что гармоническая в бесконечной области функция
ограничена на бесконечности.
Определение гармонической функции относится только к случаю открытой области
(т. е. открытого связного множества); если говорят о функции, гармонической в замкнутой области, то под этим понимают, что данная функция гармонична в более широкой открытой области.
Говорят, что функция является гармонической (или гармонична) в замкнутой области , если она
1) непрерывна в этой области,
2) гармонична во всех внутренних точках области,
3) когда область бесконечна, стремится к нулю при стремлении точки к бесконечно удаленной точке вдоль любого луча, принадлежащего области.
Определение гармонической функции не накладывает никаких ограничений на поведение функции на границе области.
Функция двух переменных не является гармонической ни в какой области, так как она не удовлетворяет однородному уравнению Лапласа
Функция гармонична в любой конечной области.
В каждой задаче, связанной с уравнением Лапласа, искомое решение выделяется из множества всех гармонических функций определенным дополнительным условием, которое чаще всего является краевым. Таким образом, возникает следующая краевая задача: найти регулярное в области решение уравнения, удовлетворяющее на границе краевому условию:
где производная по некоторому направлению (n— направление внешней нормали к ); заданные непрерывные на функции; причем всюду на .
Краевые задачи могут ставиться не только для уравнения Лапласа, но и для любых уравнений эллиптического типа.
В зависимости от вида граничного условия различают три основных вида граничной (краевой) задачи:
1. , когда ( — граница) — первая краевая задача или задача
2. , когда — вторая краевая задача или задача Неймана,
3. , когда — третья или смешанная краевая задача.
Здесь — непрерывные функции, определенные на граничной поверхности , а
означает производную, взятую в точке поверхности по направлению внешней нормали
К этим видам краевой задачи приводит изучение широкого круга стационарных физических процессов и явлений.
Если область, в которой ищется решение уравнения, ограничена, то краевая задача называется внутренней. Если же эта область является частью пространства, лежащей вне некоторой ограниченной области, то краевая задача называется внешней.
Характерной чертой уравнений эллиптического типа, существенно отличающей их от уравнений других типов, является то, что их решения полностью определяются заданием одного краевого условия. Простейшим из таких заданий является задание на контуре значения самой функции или ее нормальной производной, что и составляет содержание классических краевых задач, называемых обыкновенно, так же как и для уравнения Лапласа, первой и второй краевыми задачами или задачей Дирихле и задачей Неймана.
Задачу математической физики называют поставленной корректно, если ее решение существует, единственно и непрерывно зависит от данных задачи.
Условия, обеспечивающие корректность постановки той или иной краевой задачи, несколько различаются для разного типа задач. Но существует основная группа условий, входящих во все эти формулировки. Она сводится к следующему.
Функция, дающая решение краевой задачи (поставленной для уравнения в частных производных второго порядка) должна:
1) быть непрерывна в области, в которой ставится задача, вплоть до границы области;
2) внутри области иметь непрерывные вторые производные и удовлетворять заданному уравнению (например, уравнению Лапласа);
3) на границе области удовлетворять заданному краевому условию;
4) если область трехмерна и бесконечна, то при перемещении к бесконечно удаленной точке вдоль любого луча, принадлежащего области, стремиться к нулю.
Решения краевых задач, поставленных в трехмерных областях, удовлетворяющие перечисленным условиям, будем называть регулярными.
Решения корректно поставленных краевых задач для любого уравнения эллиптического типа всегда оказываются не менее гладкими (в смысле существования у них определенного числа непрерывных производных), чем определяющие их функции (коэффициенты уравнения и данные задачи).
Обычно во всех внутренних точках изучаемой области они даже дифференцируемы неограниченное число раз. Это свойство решений граничных задач тесно связано с тем, что к граничным задачам приводит изучение установившихся (стационарных) физических процессов.
Первая и вторая краевые задачи для уравнения Лапласа.
Краевая задача для уравнения (1) состоит в нахождении функции
класса удовлетворяющей в области этому уравнению и граничному (краевому)
условию на вида:
, где — заданные непрерывные функции на , причем , ,
Выделяют следующие типы краевых условий :
Краевое условие I рода ,
, когда ищется гармоническая функция, принимающая на границе области
заданные непрерывные значения;
Краевое условие II рода
, когда ищется гармоническая функция такая, что ее нормальная производная принимает на заданные непрерывные значения;
Краевое условие III рода
, когда ищется гармоническая функция , удовлетворяющая на границе линейному соотношению , . Данное условие называют смешанной краевой задачей, когда на различных частях границы заданы условия разного рода.
Соответствующие краевые задачи называются краевыми задачами I, II и III рода.
Для уравнения Лапласа краевая задача I рода называется задачей Дирихле;
краевая задача II рода называется задачей Неймана.
Аналогично ставятся краевые задачи для уравнения (1) и во внешности ограниченной области G (внешние краевые задачи). Отличие состоит в том, что, помимо граничного условия на S, задаются еще условия на бесконечности.
Задача Дирихле в пространстве формулируется так:
Найти функцию , удовлетворяющую внутри замкнутой поверхности уравнению Лапласа и принимающую на границе заданные значения:
То, что задача Дирихле всегда имеет решение (при некоторых весьма общих предположениях относительно и ), можно считать очевидным по физическим соображениям. Действительно, если каждая точка границы тела постоянно поддерживается при определенной температуре (которая может быть разной в разных точках границы), то в каждой точке тела установится в конце концов своя температура, которая и дает решение задачи Дирихле при данных граничных значениях. Кроме того, очевидно, что по тем же соображениям это решение будет единственным.
Задача Дирихле может быть поставлена и в двух измерениях. Если зависит только от двух пространственных координат, например и , то уравнение Лапласа (1)
принимает более простой вид:
Задача Дирихле на плоскости формулируется так:
Найти функцию , удовлетворяющую внутри замкнутой кривой уравнению Лапласа и принимающую на границе заданные значения:
Эта задача тоже имеет единственное решение. Она может возникнуть в физических задачах двух типов, которые можно пояснить на примере тела, распределение температуры в котором стационарно.
Первый тип задачи относится к стационарному распределению температуры в тонкой однородной пластинке, параллельной плоскости с теплоизолированными нижней и верхней поверхностями. Край пластинки поддерживается при определенной температуре .
Пластинка должна быть настолько тонкой, чтобы можно было пренебречь изменением температуры по ее толщине. Тогда температура и будет функцией только и .
Второй тип задачи возникает при рассмотрении стационарного распределения температуры в бесконечном однородном цилиндре, у которого образующие параллельны оси , направляющая лежит в плоскости , а боковая поверхность поддерживается при определенной температуре .
Здесь тоже остается постоянной на любой прямой, параллельной оси , проходящей в цилиндре, так что .
Заметим, что задача Дирихле решается очень просто в одномерном случае, т. е. когда в соответствующей системе координат неизвестная функция зависит только от одной из координат. В случае декартовых координат одномерное уравнение Лапласа принимает вид и его решениями являются линейные функции (стационарное распределение температуры в тонком стержне с теплоизолированной боковой поверхностью всегда линейно). Задача Дирихле имеет в этом случае решение , где , , .
Задача Неймана состоит в следующем:
Найти функцию , удовлетворяющую внутри замкнутой поверхности (или кривой) уравнению Лапласа и на границе условию:
где производная по направлению внешней нормали к , а функция, заданная
http://mathhelpplanet.com/static.php?p=chislennyye-metody-resheniya-krayevykh-zadach
http://www.myunivercity.ru/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0/%D0%9A%D1%80%D0%B0%D0%B5%D0%B2%D1%8B%D0%B5_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8_%D0%B4%D0%BB%D1%8F_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F_%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0/6494_356243_%D1%81%D1%82%D1%80%D0%B0%D0%BD%D0%B8%D1%86%D0%B02.html