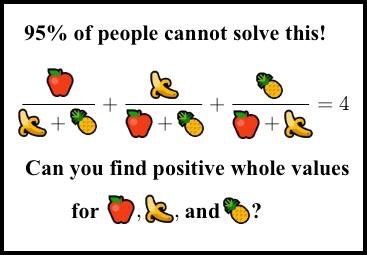Найти целочисленные решения уравнения что это такое

math4school.ru

Уравнения в целых числах

Немного теории

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

не имеет ненулевых рациональных решений для всех натуральных n > 2.

Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.

При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:

способ перебора вариантов;

применение алгоритма Евклида;

представление чисел в виде непрерывных (цепных) дробей;

разложения на множители;

решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;

метод бесконечного спуска.

Задачи с решениями

1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

2. Решить в целых числах уравнение:

а) 20х + 12у = 2013;

в) 201х – 1999у = 12.

а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

Поскольку числа 5 и 7 взаимно простые, то

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x₀ = 1273·12 = 15276, y₀ = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

3. Решить в целых числах уравнение:

а) x 3 + y 3 = 3333333;

б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).

а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;

б) в целых числах уравнение x + y = x 2 – xy + y 2 .

а) Решим данное уравнение как квадратное относительно переменной у. Получим

у = х + 9 или у = 16 – х.

Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).

Так как х, у – простые, то из равенства у = 16 – х имеем

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

б) Рассмотрим данное уравнение как квадратное уравнение относительно x:

x 2 – (y + 1)x + y 2 – y = 0.

Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?

Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид

Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:

y = xn = n(2n 2 +1) = 2n 3 +n.

Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).

6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.

Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.

Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.

Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.

Поэтому все числа x, y, z, u чётны. Тогда можно записать, что

и исходное уравнение примет вид

Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x₁, y₁, z₁, u₁ нечётны, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится на 8. А если ровно два из этих чисел нечётно, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится даже на 4. Значит,

и мы получаем уравнение

Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.

7. Докажите, что уравнение

(х – у) 3 + (y – z) 3 + (z – x) 3 = 30

не имеет решений в целых числах.

Воспользуемся следующим тождеством:

(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).

Тогда исходное уравнение можно записать в виде

(х – у)(y – z)(z – x) = 10.

Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде

Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.

8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .

если х = 1, то у 2 = 1,

если х = 3, то у 2 = 9.

Этим случаям соответствуют следующие пары чисел:

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

9. Решите следующую систему уравнений в натуральных числах:

a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).

3abc > 0, то a 3 > b 3 + c 3 ;

таким образом имеем

b 2 2 + х = у 4 + у 3 + у 2 + у.

Разложив на множители обе части данного уравнения, получим:

х(х + 1) = у(у + 1)(у 2 + 1),

х(х + 1) = (у 2 + у)(у 2 + 1)

Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:

Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х₅ = 5, х₆ = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:

Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)

Задачи без решений

1. Решить в целых числах уравнение:

б) х 2 + у 2 = х + у + 2.

2. Решить в целых числах уравнение:

а) х 3 + 21у 2 + 5 = 0;

б) 15х 2 – 7у 2 = 9.

3. Решить в натуральных числах уравнение:

4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение

5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №9. Решение уравнений в целых числах.

Перечень вопросов, рассматриваемых в теме

1. понятие диофантовых уравнений;
2. теоремы для решения уравнений в целых числах;
3. основные методы решения уравнений в целых числах.

Глоссарий по теме

Диофантовыми уравнениями называются уравнения вида

Неопределенные уравнения – уравнения, содержащие более одного неизвестного. Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

Теорема 2. Если уравнение ах + bу = 1, если НОД(а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с 1 и с не делится на d, то уравнение целых решений не имеет.

Для доказательства теоремы достаточно предположить противное.

Найти целое решение уравнения 16х — 34у = 7.

(16,34)=2; 7 не делится на 2, уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с 2 + 23 = у 2

Перепишем уравнение в виде: у 2 — х 2 = 23, (у — х)(у + х) = 23

Так как х и у – целые числа и 23 – простое число, то возможны случаи:

; ; ; ;

Решая полученные системы, находим:

; ;;;

4. Выражение одной переменной через другую и выделение целой части дроби.

Решить уравнение в целых числах: х 2 + ху – у – 2 = 0.

Выразим из данного уравнения у через х:

Так как х, у – целые числа, то дробь должна быть целым числом.

Это возможно, если х – 1 =

; ;

; ;

5. Методы, основанные на выделении полного квадрата.

Найдите все целочисленные решения уравнения: х 2 — 6ху + 13у 2 = 29.

Преобразуем левую часть уравнения, выделив полные квадраты,

х 2 — 6ху + 13у 2 = (х 2 — 6ху + 9у 2 ) + 4у 2 = (х — 3у) 2 + (2у) 2 = 29, значит (2у) 2 29.

Получаем, что у может быть равен .

1. у = 0, (х — 0) 2 = 29. Не имеет решений в целых числах.

2. у = -1, (х + 3) 2 + 4 =29, (х + 3) 2 = 25, х + 3 = 5 или х + 3 = -5

3. у = 1, (х — 3) 2 +4 =29,

(х — 3) 2 =25, х – 3 = 5 или х – 3 = -5

4. у = -2, (х + 6) 2 + 16 = 29, (х + 6) 2 = 13. Нет решений в целых числах.

5. у=2, (х-6) 2 +16=29, (х-6) 2 =13. Нет решений в целых числах.

Ответ: (2; -1); (-8; -1); (8; 1); (-2; 1).

6. Решение уравнений с двумя переменными как квадратных

относительно одной из переменных.

Решить уравнение в целых числах: 5х 2 +5у 2 +8ху+2у-2х+2=0.

Рассмотрим уравнение как квадратное относительно х:

5х 2 + (8у — 2)х + 5у 2 + 2у + 2 = 0

D = (8у — 2) 2 — 4·5(5у 2 + 2у + 2) = 64у 2 — 32у + 4 = -100у 2 — 40у – 40= = -36(у 2 + 2у + 1) = -36(у + 1) 2

Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.

-36(у + 1) 2 = 0. Это возможно при у = -1, тогда х = 1.

7. Оценка выражений, входящих в уравнение.

Решить в целых числах уравнение:

(х 2 + 4)(у 2 + 1) = 8ху

Заметим, что если – решение уравнения, то – тоже решение.

И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:

,

Пусть х > 0, у > 0, тогда, согласно неравенству Коши,

,

тогда их произведение , значит,

Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.

8.Примеры уравнений второй степени с тремя неизвестными.

Рассмотрим уравнение второй степени с тремя неизвестными: х 2 + у 2 = z 2 .

Геометрически решение этого уравнения в целых числах можно истолковать как нахождение всех пифагоровых треугольников, т.е. прямоугольник треугольников, у которых и катеты х,у и гипотенуза z выражаются целыми числами.

По формуле х = uv, , где u и v – нечетные взаимно простые числа (u > v > 0) можно найти те решения уравнения х 2 + у 2 = z 2 , в которых числа х,у и z не имеют общих делителей (т.е. взаимно простые).

Для начальных значений u и v формулы приводят к следующим часто встречающимся равенствам:

3 2 + 4 2 = 5 2 (u = 1, v = 3), 5 2 + 12 2 = 13 2 (u = 1, v = 5), 15 2 + 8 2 = 17 2 (u = 3, v = 5)

Все остальные целые положительные решения этого уравнения получаются умножением решений, содержащихся в формулах, на произвольный общий множитель а.

Разбор решения заданий тренировочного модуля

№1. Тип задания: выбор элемента из выпадающего списка

Решите уравнение 9х+22у-1=0

Решение: Решим данное уравнение, воспользовавшись теоремой 2:

2. 1 = 9 — 4∙2 = 9 — (22 — 9∙2) ∙2 = 9∙5 + 22∙(-2),

т.е. х₀= 5, у₀= -2 — решение данного уравнения

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Найдите целое решение уравнения 3х+9у=3

Решение: Решим данное уравнение: 3х+9у=3

Разделим обе части уравнения на 3, получим:

1. 3 = 1 ∙ 2 + 1
2. 1 = 3 — 1∙2, т.е. х₀= 1, у₀= 0 — решение данного уравнения

Математический детектив: поиск положительных целых решений уравнения

«Я экспериментировал с задачами кубического представления в стиле предыдущей работы Эндрю и Ричарда Гая. Численные результаты были потрясающими…» (комментарий на MathOverflow)

Вот так ушедший на покой математик Аллан Маклауд наткнулся на это уравнение несколько лет назад. И оно действительно очень интересно. Честно говоря, это одно из лучших диофантовых уравнений, которое я когда-либо видел, но видел я их не очень много.

Я нашёл его, когда оно начало распространяться как выцепляющая в сети нердов картинка-псевдомем, придуманная чьим-то безжалостным умом (Сридхар, это был ты?). Я не понял сразу, что это такое. Картинка выглядела так:

«95% людей не решат эту загадку. Сможете найти положительные целочисленные значения?»

Вы наверно уже видели похожие картинки-мемы. Это всегда чистейший мусор, кликбэйты: «95% выпускников МТИ не решат её!». «Она» — это какая-нибудь глупая или плохо сформулированная задачка, или же тривиальная разминка для мозга.

Но эта картинка совсем другая. Этот мем — умная или злобная шутка. Примерно у 99,999995% людей нет ни малейших шансов её решить, в том числе и у доброй части математиков из ведущих университетов, не занимающихся теорией чисел. Да, она решаема, но при этом по-настоящему сложна. (Кстати, её не придумал Сридхар, точнее, не он полностью. См. историю в этом комментарии).

Вы можете подумать, что если ничего другое не помогает, то можно просто заставить компьютер решать её. Очень просто написать компьютерную программу для поиска решений этого кажущегося простым уравнения. Разумеется, компьютер рано или поздно найдёт их, если они существуют. Большая ошибка. Здесь метод простого перебора компьютером будет бесполезен.

Не знаю, удастся ли уместить полное решение в статью, если не принять, что все уже знают всё необходимое об эллиптических кривых. Я могу привести здесь только краткий обзор. Основной справочный источник — это чудесная, относительно недавняя работа Бремнера и Маклауда под названием «An unusual cubic representation problem» («Необычная проблема кубического представления»), опубликованная в 2014 году в Annales Mathematicae et Informaticae.

Мы ищем положительные целочисленные решения уравнения

(я заменил обозначения переменных теми, которые используются в работе).

Первое, что нужно сделать, исследуя любое уравнение — попробовать поместить его в нужный контекст. Надо задать вопрос: что это за уравнение? Так, нас просят найти целочисленные решения, то есть это задача теории чисел. В текущей формулировке в уравнении используются рациональные функции (многочлены, делящиеся на другие многочлены), но очевидно, что мы можем домножить на общее кратное знаменателей, чтобы подчистить уравнение и получить только многочлены, то есть привести его к виду диофантова уравнения. Требование «положительности» довольно необычно, и, как мы увидим, усложняет всё.

Итак, сколько же у нас тут переменных? Вопрос кажется глупым: очевидно, что три, а именно , и . Но не торопитесь. Опытный исследователь теории чисел мгновенно заметит, что уравнение однородное. Это значит, что если является одним из решений уравнения, то решением является и . Понимаете, почему? Умножив каждую переменную на какую-нибудь постоянную ( — это просто пример), мы ничего не изменим, потому что константа в каждой из частей сокращается.

Это значит, что уравнение только притворяется трёхмерным. На самом деле оно двухмерно. В геометрическом представлении у нас есть поверхность (одно уравнение с тремя переменными в общем случае задаёт двухмерную поверхность. В целом, уравнений с переменными задают -мерное многообразие, где ). Но эта поверхность на самом деле ограничена линией, колеблющейся и проходящей через начало координат. Получившуюся поверхность можно понять, разобравшись в том, как она рассекает единичную плоскость. Это проективная кривая.

Проще всего объянить это сведение можно так: мы можем разделить решения, какими бы они ни были, на те, при которых , и те, при которых . В первом случае у нас остаётся всего две переменные, и , а во втором мы просто можем разделить на и получить решение при . Поэтому мы можем просто искать рациональные решения в и для случая , умножать их на общий делитель и получать целочисленное решение в , и . В сущности, целочисленные решения однородных уравнений соответствуют рациональным решениям неоднородной версии, которая на одну размерность меньше.

Продолжим: какова степень нашего уравнения? Степень уравнения — это максимальная степень, любого появляющаяся в уравнении одночлена, где «одночлен» — это произведение нескольких переменных, чья «степень» является количеством перемножаемых одночленов. Например, будет одночленом степени .

Поведение диофантовых уравнений сильно зависит от их степени. В целом:

• Со степенью всё просто.
• Степень полностью проанализирована и может быть решена довольно элементарными способами.
• Степень — это обширный океан глубокой теории и миллион нерешённых проблем.
• Степень и выше… Очень, очень сложны.

Мы имеем степень . Почему? Мы просто умножаем на делители:

Даже без раскрывания скобок можно увидеть, что степень равна : мы никогда не перемножаем более трёх переменных за раз. У нас получатся части типа , и , но никогда не будет чего-то больше трёх множителей. Если провести преобразования, то уравнение будет иметь вид

Вы можете возразить, что умножение на делители невозможно, если какие-то из них оказываются равны . Это верно — действительно, наше новое уравнение имеет несколько решений, не соответствующих исходному уравнению. Но на самом деле это хорошо. Версия с многочленами добавляет к оригиналу несколько «заплаток» и с ним становится проще работать. Нам просто нужно будет проверять, не исчезают ли исходные делители при каждом конкретном решении.

На самом деле уравнение с многочленами легко решить, например, , , . Это хорошо: у нас есть рациональное решение (рациональная точка). Это значит, что наше кубическое уравнение (степень = 3) на самом деле является эллиптической кривой.

Когда обнаруживаешь, что уравнение представляет собой эллиптическую кривую, то а) радуешься и б) отчаиваешься, потому что предстоит ещё много чего изучить. Это уравнение — прекрасный пример того, как мощную теорию эллиптических кривых можно применить к нахождению безумно сложно определяемых решений.

Первое, что обычно делают эллиптической кривой — приводят её в вейерштрассову форму. Это уравнение, которое выглядит как

(это называется развёрнутой вейерштрассовой формой. Она необязательна, но иногда более удобна).

Обычно любую эллиптическую кривую можно привести к такому виду (если вы только не работаете над полями с малыми характеристиками, но здесь нам не нужно о них волноваться). Объяснять способ поиска правильного преобразования было бы слишком долго, поэтому просто знайте, что это абсолютно механический процесс (критически важно в нём то, чтобы была хотя бы одна рациональная точка, которая у нас есть). Существуют разные пакеты вычислительной алгебры, которые сделают всё за вас.

Но даже если вы не знаете. как найти преобразование, проверить его очень просто, по крайней мере, это выполняется чисто механически. Необходимое преобразование в нашем случае задаётся страшно выглядящими формулами

Я знаю, что они похожи на неизвестно откуда взявшуюся магию вуду, но поверьте, это не так. Получив эти преобразования, с помощью монотонных, но довольно простых алгебраических расчётов мы покажем, что

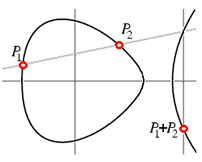
Это уравнение, хоть и выглядит совсем по-другому, на самом деле является достоверной моделью исходного. Графически оно выглядит так — типичная эллиптическая кривая с двумя вещественными частями:

«Рыбий хвост» справа растёт «в бесконечность и дальше». Овальная фигура слева является замкнутой и оказывается для нас довольно интересной.

Имея любое решение этого уравнения, мы можем восстановить необходимые значения , , с помощью уравнений

(Помните, что триплет нужно воспринимать проективно – какие бы значения вы ни получили с помощью этих уравнений, их всегда можно умножить на любую константу).

Два показанных нами отображения, из , , в , и наоборот, показывают, что эти два уравнения «одинаковы» с точки зрения теории чисел: рациональные решения одного дают рациональные решения другого. Технически это называется бирациональной эквивалентностью, а она является фундаментальным понятием алгебраической геометрии. Как мы уже заметили, могут существовать точки-исключения, которые не отображаются правильно. Это случаи, когда , или оказываются равны . Это привычная расплата в случае бирациональной эквивалентности, и она не должна вызывать никаких волнений.

Давайте рассмотрим пример.

На эллиптической кривой (2) есть хорошая рациональная точка:

, . Возможно, её не так просто найти, но очень просто проверить: просто вставьте эти значения и вы увидите, что две половины одинаковы (я выбирал эту точку не случайным образом, но пока это неважно). Можно просто проверить, какие значения , , она нам даёт. Мы получаем , , , и поскольку мы можем умножить на общий делитель, то результаты преобразуются в , , .

как можно с лёгкостью убедиться. Это простое решение нашего исходного уравнения в целых числах, но, увы, не в положительных целых. Это решение непросто вывести вручную, но и несложно получить без всей этой рассматриваемой здесь махины, приложив немного терпения. Самая сложность заключается в положительных решениях.

Теперь, получив рациональную точку на эллиптической кривой, например, на нашей кривой (2), можно начать генерировать другие с помощью техники хорд и касательных, рассмотренной в предыдущей статье на Quora.

Для начала прибавим нашу точку к ней самой, найдя касательную к кривой в точке и определив, где она снова встречается с кривой. Результат будет немного пугающим:

и снова эта новая точка соответствует значениям , , , являющимся решением исходного уравнения

Это решение определённо непросто найти вручную, но оно всё ещё под силу компьютеру. Однако оно по-прежнему неположительно.

Не пугаясь неудач, мы продолжаем вычислять , что можно определить соединением прямой линией и и нахождением третьей точки пересечения с кривой. И снова мы вычисляем , , , и снова результат неположителен. То же самое будет и с , и с , и так далее… пока мы не наткнёмся на .

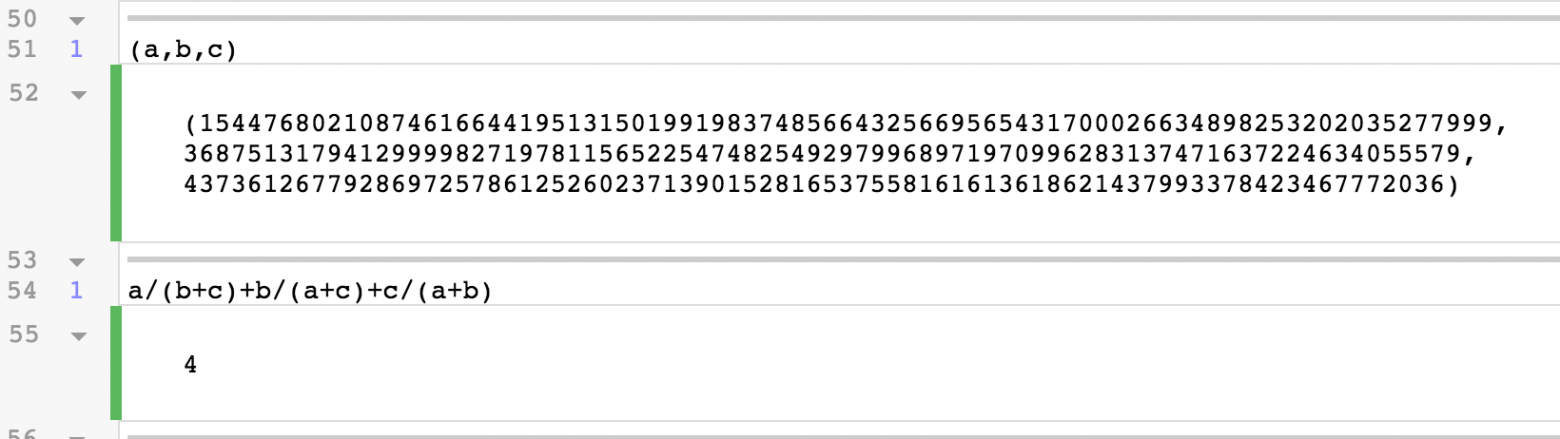
Его определённо непросто найти, но с помощью нашей машинерии нам достаточно повторить девять раз простую геометрическую процедуру. Соответствующие значения , , потрясающи:

a=154476802108746166441951315019919837485664325669565431700026634898253202035277999,
b=36875131794129999827197811565225474825492979968971970996283137471637224634055579,
c=4373612677928697257861252602371390152816537558161613618621437993378423467772036

Это 80-разрядные числа! Вы никак не смогли бы найти 80-разрядные числа на компьютере с помощью простого перебора. Выглядит невероятным, но вставив эти огромные числа в простое выражение , мы действительно получим ровно .

Фактически, они являются наименьшими решениями задачи. Если мы продолжим прибавлять к самой себе точку , то при этом просто будут расти делители. Непросто это доказать, потому что всегда есть вероятность сокращения, но теория высот для эллиптической кривой позволяет нам показать, что эти астрономические числа на самом деле являются простейшим решением уравнения.

Вернёмся к теории. Эллиптическая кривая над рациональными значениями имеет ранг, который является количеством точек, необходимых, чтобы использовать для метод хорд и касательных и быть уверенным, что мы рано или поздно найдём все рациональные точки на кривой. Наша эллиптическая кривая (2) имеет ранг 1. Это значит, что у неё есть бесконечное количество рациональных точек, но все они получаются из единственной, которая является ничем иным, как нашей точкой . Алгоритмы вычисления ранга и нахождения такого генератора далеки от тривиальных, но SageMath (теперь имеющий название CoCalc) выполняет их меньше чем за секунду всего в нескольких строках кода. Мой код можно посмотреть здесь. Он воспроизводит всё решение с нуля, но, конечно же, использует встроенные методы Sage для работы с эллиптическими кривыми.

В нашем случае точка лежит на овальной части кривой, как и точки для любого положительного целого . Они «кружатся» по овалу и постепенно довольно равномерно по нему распределяются. Это очень удачно, потому что только небольшая часть этого овала даёт положительные решения в отношении , , : это выделенная жирным часть графика ниже, взятого из работы Бремнера и Маклауда.

Точки , , и так далее, не лежат на выделенной части, а — лежит, именно так мы и получили наши 80-разрядные положительные решения.

Бремнер и Маклауд изучили, что происходит, если мы заменяем чем-то другим. Если вы думаете, что решения будут большими, то подождите, пока не увидите, какими окажутся решения при результате . Вместо 80 разрядов нам понадобится 398 605 460 разрядов. Да, это только количество разрядов решения. Если заменить результат на , то решение будет содержать триллионы разрядов. Триллионы. Для этого невинно выглядящего уравнения:

Поразительный пример того, как диофантовы уравнения с небольшими коэффициентами могут иметь огромные решения. Это внушает не просто трепет, а ощущение бездонности. Отрицательное решение десятой проблемы Гильберта означает, что рост решений при увеличении коэффициентов — это невычислимая функция, потому что если бы она была вычисляемой, то у нас был бы простой алгоритм решения диофантовых уравнений, а его не существует (ни простого, ни сложного). Соответствие 80-разрядные числа, числа из сотен миллионов разрядов и триллионы разрядов даёт нам небольшое представление о первых, небольших шагах этой чудовищной невычислимой функции. Немного измените числа в уравнении, и решения запросто превзойдут всё, что может вместиться в нашу жалкую, крошечную Вселенную.

Вот такое удивительно хитрое небольшое уравнение.

Благодарю пользователя MrShoor, приславшего мне ссылку на эту интересную статью.