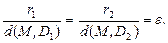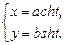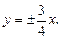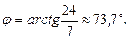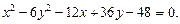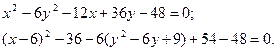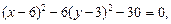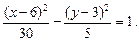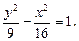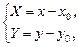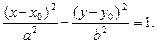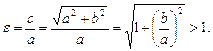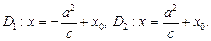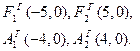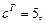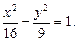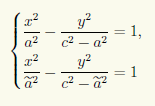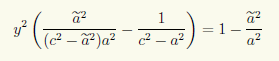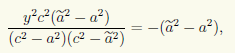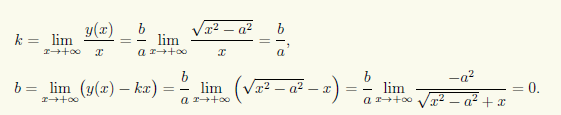Симметрии графиков функций
Прямая х=а является осью симметрии графика функции у=f(x) тогда и только тогда, когда для любого $x\in D(f)$ выполняется равенство f(x)=f(2a-x).
Прямая х=а является осью симметрии графика функции f в том и только в том случае, когда для любого х из ее области определения выполняется равенство f(a+х)=f(a-х).
Точка (а, b) является центром симметрии графика функции у=f(x) тогда и только тогда, когда для любого $x\in D(f)$ выполняется равенство f(x)+f(2а-х)=b.
Точка (а, b) является центром симметрии графика функции f в том и только в том случае, когда для любого х из ее области определения выполняется равенство f(a+х)+f(a-х)=b.
Пример 1: Сколько вертикальных осей симметрии может иметь график периодической функции?
Ответ: Если график функции f с периодом Т имеет ось симметрии х=а, то скорее всего — из геометрических соображений — осью симметрии будет и прямая х=а+Т. Но так как прямая х=с является осью симметрии графика функции у=f(x) тогда и только тогда, когда для любого $x\in D(f)$ выполняется равенство f(x)=f(2с-х), то для прямой х=а+Т надо проверить выполнение равенства f(а+Т)=f(2а-а-Т), или f(a+Т)=f(aТ), a это равенство верно.
Так как периодов у периодической функции бесконечно много, то и осей симметрии бесконечно много, если, конечно, есть хотя бы одна.
Пример 2: График функции у=f(x) имеет вертикальную ось и центр симметрии. Что можно сказать о графике функции у=2f(x)-1?
Ответ: Так как график функции у=f(x) имеет вертикальную ось симметрии, например х=а, то для всякого х имеет место равенство f(a+х)=f(а-х), а тогда очевидно 2f(a+х)-1=2f(а-x)-1, так что функция у=2f(x)-1 имеет ту же ось симметрии. Если же график функции у=f(x) имеет центр симметрии, например, Q=(а, b), то для всякого х имеет место равенство f(а+х)+f(а-х)=2b, и в этом случае (2f(а+х)-1)+(2f(а-х)-1)=2b
Презентиция по математики «Симметрия в построении графиков функции»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
XVI научная конференция молодых исследователей «Шаг в будущее»
Симметрия в построении графиков функции
Автор : Шматова Алёна Сергеевна, ученица 10 «А» класса, Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа №44
Научный руководитель: Шибко Елена Николаевна, учитель математики, Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа №44
г. Сургут 2014 г.
Содержание
Аннотация
Данная исследовательская работа направлена на изучение использования симметрии в жизни человека и математических науках; изучение теоретической стороны темы; проведение практической работы по теме «Симметрия». Изучив проблему симметрии, мы увидели, что симметрия присутствует и в прошлом, и в настоящем, и в будущем. Симметрия – это не только математическое понятие. Его заимствовали из природы. А так как человек – это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии. Симметрия в живой природе: в животном и растительном мире, передаётся генетически из поколения в поколение.
Введение
Симметрия… является той идеей, посредством
которой человек на протяжении веков пытался
постичь и создать порядок, красоту и
Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека, и употреблялось скульпторами ещё в V веке до н. э.
Слово «симметрия» греческое. Оно означает «соразмерность», «пропорциональность», одинаковость в расположении частей. Его широко используют все без исключения направления современной науки.
Об этой закономерности задумывались многие великие люди. Например, Л.Н. Толстой говорил: «Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врождённое чувство. На чём же оно основано?»
Действительно, симметричность приятна глазу. Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, — всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии.
Симме́три́я (др.-греч. συμμετρία — «соразмерность»), в широком смысле — неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.
С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Отметим, например, симметрию, свойственную бабочке и кленовому листу, симметрию автомобиля и самолета, симметрию в ритмическом построении стихотворения и музыкальной фразы, симметрию орнаментов и бордюров, симметрию атомной структуры молекул и кристаллов. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
узнать где и как используется симметрия в жизни человека.
Выяснить, кто первым обратил внимание на использование симметрии в жизни человека.
Выявить где используется центральная симметрия.
Выявить где используется осевая симметрия.
Выяснить, как легче строить графики симметричных функций.
Выявить, можно ли наблюдать симметрию в неживой природе.
Проанализировать симметрию в природе и связь природы с математикой.
Определить связь между симметрией в природе, математики, физике, архитектуры.
Выявить симметричные функции.
Доказать, что существуют такие функции, которые связанны с природой.
Гипотеза: Симметрия существует в природе, математики, физике, архитектуре.
Объект исследования: симметрия в природе, математики, физике, архитектуре.
Предмет исследования: симметричные функции .
Методы исследования: изучение, анализ и обобщение данных научной литературы, наблюдение, фотографирование, анкетирование, интервьюирование, эксперимент, количественный и качественный учет данных, обработка и анализ полученных данных.
Глава 1. Симметрия
Симметрия является той идеей, посредством которой человек на протяжении веков пытался
постичь и создать порядок, красоту и
Понятие симметрии проходит через всю многовековую историю человеческого творчества. Многие народы с древних времён владели представлением о симметрии в широком смысле — как эквиваленте уравновешенности и гармонии.
Формы восприятия и выражения во многих областях науки и искусства, в конечном счёте, опираются на симметрию, используемую и проявляющуюся в специфических понятиях и средствах, присущих отдельным областям науки и видам искусства.
Действительно, симметричные объекты окружают нас буквально со всех сторон, мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. Симметрия противостоит хаосу, беспорядку. Получается, что симметрия – это уравновешенность, упорядоченность, красота, совершенство.
Весь мир можно рассмотреть как проявление единства симметрии и асимметрии. Асимметричное в целом сооружение может являть собой гармоничную композицию из симметричных элементов.
Симметрия многообразна, вездесуща. Она создает красоту и гармонию.
Идея симметрии часто является отправным пунктом в гипотезах и теориях учёных прошлых веков, веривших в математическую гармонию мироздания и видевших в этой гармонии проявление божественного начала. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. В своих размышлениях над картиной мироздания человек с давних времен активно использовал идею симметрии.
Глава 2. Виды симметрии
Симметрия (от греческого symmetria – «соразмерность») — понятие, означающее сохраняймость, повторяемость, «инвариантность» каких-либо особенностей структуры изучаемого объекта при проведении с ним определенных преобразований.
Что же такое «симметрия»? Когда мы смотрим в зеркало, мы наблюдаем в нем свое отражение — это пример «зеркальной» симметрии. Зеркальное отражение — это пример так называемого «ортогонального» преобразования, изменяющего ориентацию.
«симметрией» в математике понимается такое преобразование пространства (плоскости), при котором каждая точка M переходит в другую точку M’ относительно некоторой плоскости (или прямой), когда отрезок MM’ является перпендикулярным плоскости (или прямой) и делится ею пополам. Плоскость (прямая) называется при этом плоскостью (или осью) симметрии.
К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии, центр симметрии. Плоскостью симметрии P называется такая плоскость, которая делит фигуру на две зеркально равные части, расположенные друг относительно друга так, как предмет и его зеркальное отражение. Например, изображенный на Рис.1 слева равнобедренный треугольник ABC высотой BD разделяется на две зеркально равные половины ABD и BCD; при этом высота BD является «следом» плоскости симметрии P, перпендикулярной плоскости треугольника. На рис. 1 справа изображен также прямоугольный параллелепипед (кирпичик, спичечный коробок), который имеет три взаимно перпендикулярные плоскости симметрии 3P. Нетрудно установить, что куб обладает девятью плоскостями симметрии — 9P.
Осью симметрии L называется такая прямая линия, вокруг которой симметричная фигура может быть повернута несколько раз таким образом, что каждый раз фигура «самосовмещается» сама с собой в пространстве. Число таких поворотов вокруг оси
симметрии называется порядком оси. Например, равносторонний треугольник имеет ось симметрии L3, то есть существуют три способа поворота треугольника вокруг оси, при котором происходит его «само совмещение». Ясно, что квадрат имеет ось симметрии L4, а пентагон — L5. Конус также имеет ось симметрии, причем, поскольку число поворотов конуса вокруг своей оси симметрии, приводящих к «само совмещению» бесконечно, то говорят, что конус имеет ось симметрии типа.
Наконец, центром симметрии C называется такая особая точка внутри фигуры, характеризующаяся тем, что любая проведенная через точку прямая по обе стороны от нее и на равных расстояниях встречает одинаковые (соответственные) точки фигуры. «Идеальным» примером такой фигуры является шар, центр которого и является его центром симметрии.
Симметрия широко встречается в объектах живой и неживой природы. Например, симметрия в химии отражается в геометрической конфигурации молекул. Так, например, молекула метана СH4 обладает симметрией тетраэдра. Понятие «симметрии» является центральным при исследовании кристаллов. При этом симметрия внешних форм кристаллов определяется симметрией его атомного строения, которая обуславливает и симметрию физических свойств кристалла.
Особенно широко понятие «симметрии» применительно к физическим законам используется в современной физике. Если законы, устанавливающие соотношения между величинами или определяющие изменение этих величин со временем, не меняются при определенных операциях (преобразованиях), которым может быть подвергнута система, то говорят, что эти законы обладают симметрией (или инвариантны) относительно данных преобразований. Например, закон тяготения действует в любой точки пространства, то
есть он является инвариантным по отношению переноса системы как целого в пространстве.
По мнению ученого-энциклопедиста академика В.И. Вернадского, «симметрия . охватывает свойства всех полей, с которыми имеет дело «физик и химик».
На явление симметрии в живой природе обратили внимание еще пифагорейцы в связи с развитием ими учения о гармонии. Установлено, что в природе наиболее распространенной «Зеркальной» симметрией обладает бабочка, листок или жук (Рис.2) и часто такой вид симметрии называется «симметрией листка» или «билатеральной симметрией». К формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево и часто такой вид симметрии называется «ромашко-грибной» симметрией.

Еще в 19-м веке исследования в этой области привели к заключению, что симметрия природных форм в значительной степени зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса. В результате был найден следующий закон, которому подчиняются формы природных тел:
Все то, что растет или движется по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой («ромашко-грибной») симметрии (рис.3б). Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии – «симметрии листка» (одна плоскость симметрии) рис.3а.
рис.3а билатеральная симметрия — «симметрия листка»

Принцип «симметрии» широко используется в искусстве. Бордюры, используемые в архитектурных и скульптурных произведениях, орнаменты, используемы в прикладном искусстве, — все это примеры использования симметрии.
Принцип симметрии очень часто используется совместно с принципом «золотого сечения». Таким примером может служить картина Рафаэля «Обручение Марии».
Глава 3. Симметрия в построении графиков функции.
Простейшими видами пространственной симметрии являются центральная, осевая, зеркально — поворотная и симметрия переноса.
Две точки А и А 

Точка М 



Преобразование фигуры F в фигуру F 
Если при переносе плоской фигуры F вдоль заданной прямой АВ на расстояние а (или кратное этой величине) фигура совмещается сама с собой, то говорят о переносной симметрии. Прямая АВ называется осью переноса, расстояние а элементарным переносом или периодом.
Определение 1. Функцию y = f(x) , x 
Свойство 1. График четной функции симметричен относительно оси ОУ.
Доказательство. Пусть y= f(x) — четная функция, тогда f(-x) = f(x). Рассмотрим произвольную точку графика M(x 




у = f(х) — четная, то f( х 



Определение 2. Функцию y = f(x), x 
Свойство 2. График нечетной функции симметричен относительно начала координат.
Доказательство. Пусть y = f(x) — нечетная функция, тогда f(-x) = -f(x). Рассмотрим произвольную точку графика M(x 







Точки графика М и M 
а) у=х
Докажем, что ось ОУ является осью симметрии данного графика.
у(-а) = (-а) 



Докажем, что никакая другая прямая не будет являться осью симметрии.
Предположим, что некоторая прямая х = х 
у (x 











= х 

прямая х = х 
б) y= ax 
Докажем, что для данного графика ось симметрии будет проходить через вершину параболы (x 

Первую координату вершины параболы можно вычислить по формуле:
. Рассмотрим произвольную точку графика M(x 

М 


у(x 









Значит, точки М и М 

в) у= х 
Докажем, что начало координат будет точкой симметрии данного графика.
у(-x) = (-x) 


f => f(-x) =-f(x) => — нечетная функция (определение 2) => центром
симметрии данного графика является начало координат (доказательство 2).
Определение 3. Две точки А и А 


Графиком данной функции является прямая.
1. Каждая точка, принадлежащая этой прямой, будет являться ее центром симметрии, т.е. у этого графика бесконечно много центров симметрии.
Рассмотрим точку М(x 







точки М 



у = k(2 x 

y= 2kx 
Следовательно, точка М 
Осью симметрии данного графика будет являться прямая параллельная оси ОУ и проходящая через некоторую координату (x 
у(-х) = k|-x|+b = k|x| + b = у(х) => функция y = k|x| + b является четной (определение 1) Значит, она симметрична относительно оси ОУ.
з)y = а 
у(-х) = а(-х) 

и) y=│ax 
При построении данного графика, сначала строим график у=ах 
Так же мы знаем, что через вершину параболы ( х 

Из свойств (1) и (2), следует, что ось симметрии параболы является осью данного графика.
Заключение
С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
Существует множество видов симметрии, как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.
Симметрия в алгебре и геометрии имеет большое значение. Я рассмотрела основные теории, связанные с симметрическими системами уравнений. Научилась решать симметрические системы уравнений, и узнала кое-что новое про симметрию графиков функций. Выбранная тема актуальна, так как в средней школе не рассматриваются все виды симметрий в алгебре и геометрии.
Как найти центр гиперболы по уравнению
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой (y=frac ), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac ) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=frac -1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
Дробь (color >) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.
5. Гипербола нечетная функция.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: База знаний, Уроки Tag: Гипербола Leave a comment
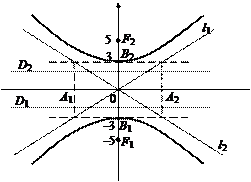
Гиперболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению
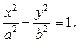
где 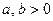
Параметры гиперболы:
Точки F1(–c, 0), F2(c, 0), где 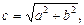
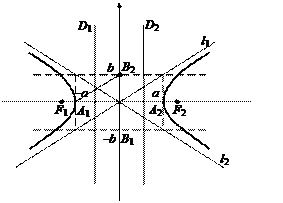 |
Величина 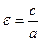
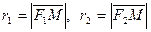
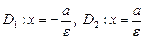
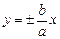
Для гиперболы справедливо: ε > 1, директрисы не пересекают границу и внутреннюю область гиперболы, а также обладают свойством
Говорят, что уравнение
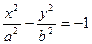
задает уравнение гиперболы, сопряженной данной (рис. 20). Его можно записать также в виде
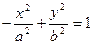
В таком случае ось 
 |
Точки гиперболы обладают важным характеристическим свойством: абсолютное значение разности расстояний от каждой из них до фокусов есть величина постоянная, равная 2a (рис. 19).
Для параметрического задания гиперболы в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на гиперболе, и положительным направлением оси Ox:
Пример 1. Привести уравнение гиперболы
к каноническому виду, найти еепараметры, изобразить гиперболу.
Решение. Разделим левую и правую части заданного уравнения на 144: 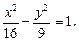
Сделаем чертеж. Для этого по осям Ox и Oy симметрично относительно точки (0, 0) отложим отрезки А1А2 = 2а = 8 и В1В2 = 2b = 6 соответственно. Через полученные точки А1(–4, 0), А2(4, 0), В1(0, –3), В2(0, 3) проведем прямые, параллельные координатным осям. В результате получим прямоугольник (рис. 21), диагонали которого лежат на асимптотах гиперболы. Строим гиперболу
 |
Для нахождения угла φ между асимптотами гиперболы воспользуемся формулой


откуда получаем
Пример 2. Определить тип, параметры и расположение на плоскости кривой, уравнение которой
Решение. С помощью метода выделения полных квадратов упростим правую часть данного уравнения:
которое делением на 30 приводится к виду
Это уравнение гиперболы, центр которой лежит в точке 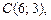
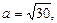
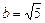
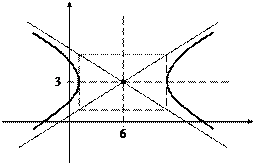 |
Пример 3. Составить уравнение гиперболы, сопряженной относительно гиперболы 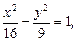
Решение.Уравнение гиперболы, сопряженной данной, –
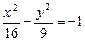
Действительная полуось b = 3, мнимая – а = 4, половина междуфокусного расстояния 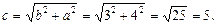
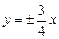
 |
Заметим, что для сопряженных гипербол общими элементами являются вспомогательный «прямоугольник» и асимптоты.
Пример 4. Написать уравнение гиперболы с полуосями a и b (a > 0, b > 0), если известно, что ее главные оси параллельны координатным осям. Определить основные параметры гиперболы.
Решение. Искомое уравнение можно рассматривать как уравнение гиперболы 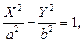
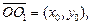
получим уравнение гиперболы
Определим параметры. Центр гиперболы определяет точка O¢(x0; y0), а значит, действительная ось задается уравнением x = x0,а мнимая – уравнением y = y0. Ее вершинами являются точки 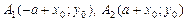
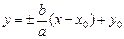
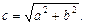
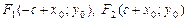
Директрисы D1 и D2 задаются уравнениями
Пример 5.Написать уравнение гиперболы, имеющей вершины в фокусах эллипса 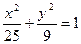
Решение.Уравнение 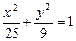
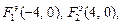
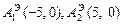
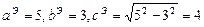
Тогда для искомой гиперболы известно, что
Значит, основные параметры гиперболы есть:
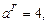
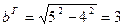
Используя данную информацию, приходим к уравнению гиперболы
Задания для самостоятельного решения
Дата добавления: 2014-12-16 ; Просмотров: 6979 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Определение 7.2. Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой.
Замечание 7.2. Говоря о разности расстояний, подразумевают, что из большего расстояния вычитается меньшее. Это значит, что на самом деле для гиперболы постоянным является модуль разности расстояний от любой ее точки до двух фиксированных точек. #
Определение гиперболы аналогично определению эллипса. Различие между ними лишь в том, что для гиперболы постоянна разность расстояний до фиксированных точек, а для эллипса — сумма тех же расстояний. Поэтому естественно, что у этих кривых много общего как в свойствах, так и в используемой терминологии.
Фиксированные точки в определении гиперболы (обозначим их F1 и F2) называют фокусами гиперболы. Расстояние между ними (обозначим его 2с) называют фокальным расстоянием, а отрезки F1M и F2M, соединяющие произвольную точку M на гиперболе с ее фокусами, — фокальными радиусами.
Вид гиперболы полностью определяется фокальным расстоянием |F1F2| = 2с и значением постоянной величины 2а, равной разности фокальных радиусов, а ее положение на плоскости — положением фокусов F1 и F2.
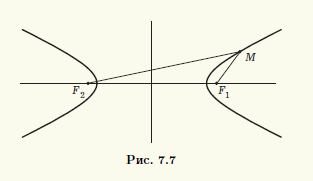
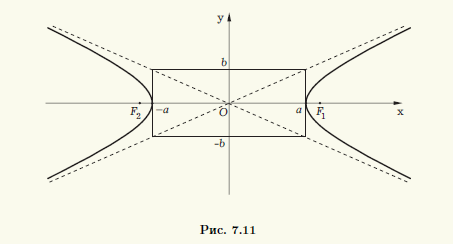
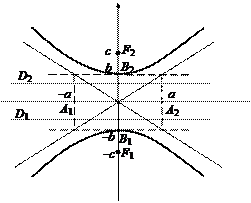
Из определения гиперболы следует, что она, как и эллипс, симметрична относительно прямой, проходящей через фокусы, а также относительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 7.7). Первую из этих осей симметрии называют действительной осью гиперболы, а вторую — ее мнимой осью. Постоянную величину а, участвующую в определении гиперболы, называют действительной полуосью гиперболы.
Середина отрезка F1F2, соединяющего фокусы гиперболы, лежит на пересечении ее осей симметрии и поэтому является центром симметрии гиперболы, который называют просто центром гиперболы.
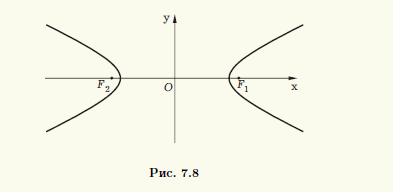
Для гиперболы действительная ось 2а должна быть не больше, чем фокальное расстояние 2с, так как для треугольника F1MF2 (см. рис. 7.7) справедливо неравенство ||F1M| — |F2M| | ≤ |F1F2|. Равенство а = с выполнено только для тех точек M, которые лежат на действительной оси симметрии гиперболы вне интервала F1F2. Отбрасывая этот вырожденный случай, далее будем предполагать, что а 2а. Согласно замечанию 7.2, гипербола состоит из тех точек M(х; у), для которых | |F1M| — — |F2M| | = 2а. Выберем прямоугольную систему координат Oxy так, чтобы центр гиперболы находился в начале координат, а фокусы располагались на оси абсцисс (рис. 7.8). Такую систему координат для рассматриваемой гиперболы называют канонической, а соответствующие переменные — каноническими.
В канонической системе координат фокусы гиперболы имеют координаты F1(c; 0) и F2(—с; 0). Используя формулу расстояния между двумя точками, запишем условие ||F1M| — |F2M|| = 2а в координатах |√((х — с) 2 + у 2 ) — √((х + с) 2 + у 2 )| = 2а, где (x; у) — координаты точки M. Чтобы упростить это уравнение, избавимся от знака модуля: √((х — с) 2 + у 2 ) — √((х + с) 2 + у 2 ) = ±2а, перенесем второй радикал в правую часть и возведем в квадрат: (х — с) 2 + у 2 = (х + с) 2 + у 2 ± 4а √((х + с) 2 + у 2 ) + 4а 2 . После упрощения получим —εх — а = ±√((х + с) 2 + у 2 ), или
√((х + с) 2 + у 2 ) = |εх + а| (7.7)
где ε = с/а. Возведем в квадрат вторично и снова приведем подобные члены: (ε 2 — 1)х 2 — у 2 = с 2 — а 2 , или, учитывая равенство ε = с/а и полагая b 2 = c 2 — a 2 ,
x 2 /a 2 — y 2 /b 2 = 1 (7.8)
Величину b > 0 называют мнимой полуосью гиперболы.
Итак, мы установили, что любая точка на гиперболе с фокусами F1(с;0) и F2(—с; 0) и действительной полуосью а удовлетворяет уравнению (7.8). Но надо также показать, что координаты точек вне гиперболы этому уравнению не удовлетворяют. Для этого мы рассмотрим семейство всех гипербол с данными фокусами F1 и F2. У этого семейства гипербол оси симметрии являются общими. Из геометрических соображений ясно, что каждая точка плоскости (кроме точек, лежащих на действительной оси симметрии вне интервала F1F2, и точек, лежащих на мнимой оси симметрии) принадлежит некоторой гиперболе семейства, причем только одной, так как разность расстояний от точки до фокусов F1 и F2 меняется от гиперболы к гиперболе. Пусть координаты точки M(х; у) удовлетворяют уравнению (7.8), а сама точка принадлежит гиперболе семейства с некоторым значением ã действительной полуоси. Тогда, как мы доказали, ее координаты удовлетворяют уравнению 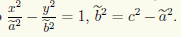
имеет хотя бы одно решение. Непосредственной проверкой убеждаемся, что при ã ≠ а это невозможно. Действительно, исключив, например, x из первого уравнения:
после преобразований получаем уравнение
которое при ã ≠ а не имеет решений, так как 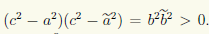
Вид гиперболы. По своему виду гипербола (7.8) заметно отличается от эллипса. Учитывая наличие двух осей симметрии у гиперболы, достаточно построить ту ее часть, которая находится в первой четверти канонической системы координат. В первой четверти, т.е. при x ≥ 0, у ≥ 0, каноническое уравнение гиперболы однозначно разрешается относительно у:
у = b/a √(x 2 — а 2 ). (7.9)
Исследование этой функции y(x) дает следующие результаты.
Область определения функции — ив этой области определения она непрерывна как сложная функция, причем в точке x = а она непрерывна справа. Единственным нулем функции является точка x = а.
Найдем производную функции y(x): y'(x) = bx/a√(x 2 — а 2 ). Отсюда заключаем, что при x > а функция монотонно возрастает. Кроме того, 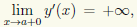
Указанная функция имеет наклонную асимптоту, это вытекает из существования двух пределов:
Наклонная асимптота описывается уравнением y = (b/a)x.
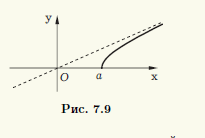
Проведенное исследование функции (7.9) позволяет построить ее график (рис. 7.9), который совпадает с частью гиперболы (7.8), содержащейся в первой четверти.
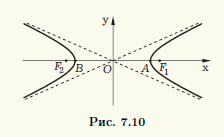
Так как гипербола симметрична относительно своих осей, вся кривая имеет вид, изображенный на рис. 7.10. Гипербола состоит из двух симметричных ветвей, расположенных по разные
стороны от ее мнимой оси симметрии. Эти ветви не ограничены с обеих сторон, причем прямые у = ±(b/a)x являются одновременно асимптотами и правой и левой ветвей гиперболы.
Оси симметрии гиперболы различаются тем, что действительная пересекает гиперболу, а мнимая, будучи геометрическим местом точек, равноудаленных от фокусов, — не пересекает (поэтому ее и называют мнимой). Две точки пересечения действительной оси симметрии с гиперболой называют вершинами гиперболы (точки A(a; 0) и B(—a; 0) на рис. 7.10).
Построение гиперболы по ее действительной (2a) и мнимой (2b) осям следует начинать с прямоугольника с центром в начале координат и сторонами 2a и 2b, параллельными, соответ-ственно, действительной и мнимой осям симметрии гиперболы (рис. 7.11). Асимптоты гиперболы являются продолжениями диагоналей этого прямоугольника, а вершины гиперболы — точками пересечения сторон прямоугольника с действительной осью симметрии. Отметим, что прямоугольник и его положение на плоскости однозначно определяют форму и положение гиперболы. Отношение b/a сторон прямоугольника определяет степень сжатости гиперболы, но вместо этого параметра обычно используют эксцентриситет гиперболы. Эксцентриситетом гиперболы называют отношение ее фокального расстояния к действительной оси. Эксцентриситет обозначают через ε. Для гиперболы, описываемой уравнением (7.8), ε = c/a. Отметим, что если эксцентриситет эллипса может принимать значения из полуинтервала [0,1) (значение 0 соответствует предельному варианту эллипса — окружности), то эксцентриситет гиперболы всегда попадает в интервал (1, + ∞).
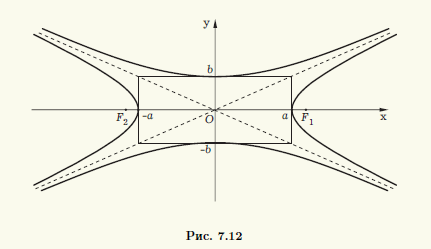
Построим прямоугольник с центром в начале системы координат Oxy и сторонами 2a, 2b, параллельными осям абсцисс и ординат соответственно. Проведем прямые y = (b/a)x и y = — (b/a)x, на которых лежат диагонали прямоугольника. Существует две гиперболы, соответствующие построенному прямоугольнику (рис. 7.12). Первая из них описывается каноническим уравнением (7.8), а вторая — уравнением
x 2 /a 2 — y 2 /b 2 = -1. (7.10)
Вторую гиперболу называют сопряженной по отношению к первой, а уравнение (7.10) — каноническим уравнением сопряженной гиперболы. Действительная и мнимая оси первой гиперболы являются соответственно мнимой и действительной осями сопряженной гиперболы, а асимптоты у них общие.
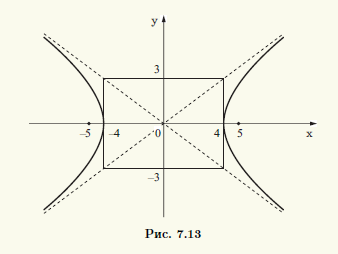
Пример 7.2. Найдем каноническое уравнение гиперболы по ее действительной полуоси a = 4 и фокальному расстоянию 2с = 10. Построим гиперболу и определим координаты ее вершин, фокусов и уравнения асимптот.
Так как действительная полуось a гиперболы известна, то, чтобы найти каноническое уравнение гиперболы, достаточно определить мнимую полуось b. Поскольку с = 5, b = √(с 2 — а 2 ), то b = √(5 2 — 4 2 ) = 3. Итак, искомое уравнение имеет вид x 2 /4 2 — y 2 /3 2 = 1. Построим прямоугольник,соответствующий заданной гиперболе (рис. 7.13). Продолжим его диагонали до асимптот ги-перболы и построим саму гиперболу. Уравнениями асимптот являются у = ±3x/4, вершины находятся в точках (±4; 0), а фокусы совпадают с точками (±5; 0).
Геометрические свойства. Геометрические свойства гиперболы во многом повторяют свойства эллипса. Вернемся к формуле (7.7). Она эквивалентна каноническому уравнению гиперболы и дает выражение для длины фокального радиуса F2M ее точки M(х; у):
|F2M| = √((х + с) 2 + у 2 ) = ±(εх + a) (7.11)
где знак плюс соответствует правой ветви гиперболы, а знак минус — левой.
Аналогично можно получить формулу для длины другого фокального радиуса, если при выводе канонического уравнения гиперболы перед первым возведением в квадрат в правую часть равенства перенести не второй, а первый квадратный радикал. При этом вместо (7.7) получим εх — a = ±√((х — с) 2 + у 2 ) , откуда
|F1M| = √((х — с) 2 + у 2 ) = ±(εх — a) (7.12)
где, как и в (7.11), знак плюс соответствует правой ветви гиперболы, а знак минус — левой. Каждое из уравнений (7.11), (7.12) является уравнением гиперболы.
Гипербола не проходит через свои фокусы (при 0 2 /c = (c 2 — a 2 )/c = b 2 /c
Гипербола также имеет и оптическое свойство, аналогичное оптическому свойству эллипса. Оно состоит в том, что лучи, вышедшие из одного фокуса, после отражения от ближайшей ветви гиперболы распространяются так, будто вышли из другого фокуса (рис. 7.15).
http://infourok.ru/prezenticiya-po-matematiki-simmetriya-v-postroenii-grafikov-funkcii-4345260.html
http://hd01.ru/info/kak-najti-centr-giperboly-po-uravneniju/