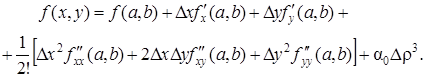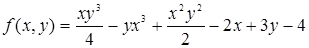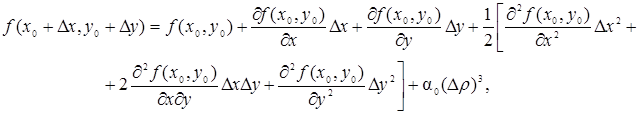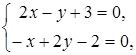Найти уравнение линии уровня проходящей через точку m0

Компьютерный чертеж. Выполним

Линии уровня и градиент функции двух переменных

Линией уровня функции называется множество точек из области определения на плоскости , для которых значение функции постоянно и равно , то есть

Построить график функции . Записать уравнение линии уровня, проходящей через точку .

Графиком линейной функции двух переменных является плоскость в пространстве. Для функции график представляет собой плоскость, проходящую через точки , , .

Линиями уровня функции являются параллельные прямые, уравнение которых или или .

Найдем уравнение линии уровня, проходящей через точку , для этого подставим координаты точки в уравнение и найдем значение параметра :

уравнение линии уровня, проходящей через точку имеет вид

Уравнение линии уровня, проходящей через данную точку, будет

.

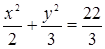
Задание для самостоятельной работы

106. Найти производную функции 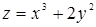в точке М(2; 1) в направлении вектора S= i+2 j.

107. Найти производную функции 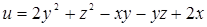в точке М(3; 1; 5) в направлении вектора S = i — 2j+ 3k.

108. Найти производную функции в точке P(1; 2) в направлении, составляющем с осью Ox угол в 60°.

109. Найти производную функции в точке M(1; 2) в направлении, идущем от этой точки к точке N(4; 6).

110. Найти производную функции 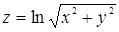в точке М(1; 1) в направлении биссектрисы первого координатного угла.

111. Найти производную функции 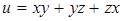в точке M(2; 1; 3) в направлении, идущем от этой точки к точке N(5; 5; 15).

112. Найти градиент функции 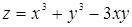в точке P(2; 1) .

113. Найти градиент функции 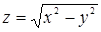в точке P(5; 3).

114. Найти градиент функции 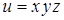в точке P(1; 2; 3).

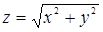
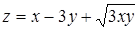
115. Найти угол между градиентами функций и в точке P(3; 4).

12. Формула Тейлора для функции двух переменных

Пусть функция двух переменных z = f(х, у) непрерывна вместе со всеми частными производными до (п + 1)-го порядка включительно в некоторой окрестности точки М(а, b). Тогда функцию двух переменных представим в виде суммы многочлена п-го порядка по степеням х – а и у – b и некоторого остаточного члена. Для случая п = 2 эта формула имеет вид

, (41)

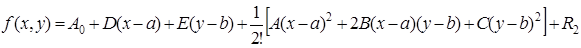
где коэффициенты А₀, D, E, А, В, С не зависят от х и у, а R₂ – остаточный член, структура которого аналогична структуре остаточного члена в формуле Тейлора для функции одной переменной.

Применим формулу Тейлора для функции f(х, у) одной переменной у, считая х постоянным (ограничимся членами второго порядка):

, (42)

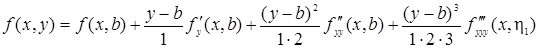
где h₁ = b + q₁(у – b), 0 3 ограничен в рассматриваемой области; обозначим его через a₀.

Тогда можно написать

Формула Тейлора (46) в принятых обозначениях для случая п = 2 примет вид

При любом п формула Тейлора имеет аналогичный вид.

Задание для самостоятельной работы

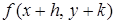
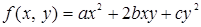
116. Разложить по целым положительным степеням k и h, если .

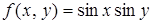
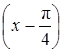
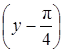
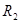
117.Разложить функцию по степеням и . Найти члены первого и второго порядка и (остаточный член второго порядка).

118. Функцию 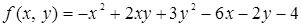разложить по формуле Тейлора в окрестности точки (-2; 1).

119. Найти приращение, получаемое функцией 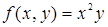при переходе от значений x = 1, y = 1 к значениям x = 1 + h, y = 1 + k.

120. Найти приращение, получаемое функцией

при переходе от значений x = 1, y = 2 к значениям x = 1 + h, y = 1 + k. Ограничиваясь членами 2-го порядка включительно, вычислить f (1,02; 2,03).

121. Разложить по формуле Тейлора в окрестности точки (1; 1) до членов 2-го порядка включительно функцию .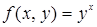

122. Разложить по формуле Тейлора в окрестности точки (1; -1) до членов 3-го порядка включительно функцию .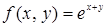

123. Вывести приближенную формулу с точностью до членов 2-го порядка относительно величин a и b для выражения .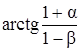

124. Используя формулу Тейлора до членов 2-го порядка, вычислить приближенно .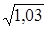

125. Разложить в ряд Тейлора при a = 0, b = 0 функцию

.

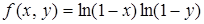
13. Максимум и минимум функции нескольких переменных

для всех точек (х, у), достаточно близких к точке (х₀, у₀) и отличных от нее.

Определение 2.Совершенно аналогично говорят, что функция z = f(х, у) имеет минимум в точке М₀(х₀, у₀), если

Пример 41. Функция 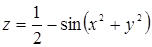при х = 0, у = 0 (т.е. в начале координат) достигает максимума.

Действительно, f(0, 0) = ½. Возьмем внутри окружности х 2 + у 2 = p/6 точку (х, у), отличную от точки (0, 0); тогда при 0 2 + у 2 2 + у 2 )> 0 и поэтому 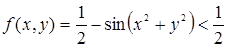, т.е. f(х, у) 0 при всех достаточно малых приращениях независимых переменных, то функция f(х, у) достигает минимума в точке М₀(х₀, у₀).

Эти формулировки переносятся без изменения на функцию любого числа переменных.

Теорема 1 (необходимое условие экстремума). Если функция z = f(х, у) достигает экстремума при х = х₀, у = у₀, то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не существует.

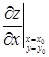
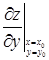
Действительно, дадим переменной у определенное значение, именно у = у₀. Тогда функция f(х, у₀) будет функцией одной переменной х. Так как при х = х₀ она имеет экстремум (максимум или минимум), то, следовательно, или равно нулю, или не существует. Совершенно аналогично можно доказать, что или равно нулю, или не существует.

Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции, но позволяет находить эти значения в тех случаях, в которых мы заранее уверены в существовании максимума или минимума. В противном случае требуется дополнительное исследование.

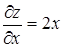
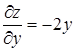
Так, например, функция z = x 2 – y 2 имеет производные , , которые обращаются в нуль при х = 0 и у = 0. Но эта функция при указанных значениях не имеет не максимума, ни минимума. Действительно, эта функция равна в нулю в начале координат и принимает в как угодно близких точках от начала координат как положительные, так и отрицательные значения. Следовательно, значение нуль не является ни максимум ни минимум.

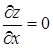
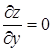
Точки, в которых (или не существует) и (или не существует), называются критическими точками функции z = f(х, у). Если функция достигает экстремума в какой-либо точке, то (в силу теоремы 1) это может случиться в критической точке.

Для исследования функции в критических точках установим достаточные условия экстремума функции двух переменных.

Теорема 2. Пусть в некоторой области, содержащей точку М₀(х₀, у₀), функция f(х, у) имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, точка М₀(х₀, у₀) является критической точкой функции f(х, у), т.е.

, .

и ;

и ;

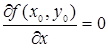
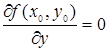
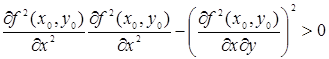
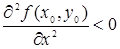
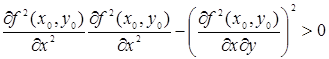
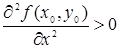
3) f(х, у) не имеет ни максимум, ни минимума, если

;

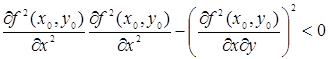
4) если 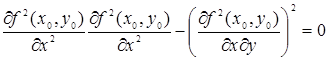, то экстремум может быть и может не быть (в этом случае требуется дополнительное исследование).

Доказательство. Напишем формулу Тейлора второго порядка для функции f(х, у). Полагая а = х₀, b = у₀, х = х₀ + Dх, у = у₀ + Dу, будем иметь

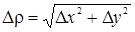
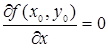
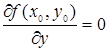
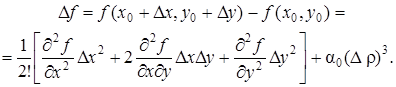
где , а a₀ стремится к нулю при Dr ® 0.

, .

(47)

Обозначим теперь значения вторых частных производных в точке М₀(х₀, у₀) через А, В, С:

, , .

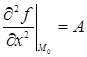
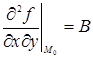
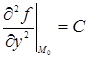
Обозначим через j угол между направлением отрезка М₀М, где М есть точка М(х₀ + Dх, у₀ + Dу), и осью Ох; тогда Dх = Dr cosj, Dу = Dr sinj. Подставляя эти выражения в формулу (47), найдем

. (48)

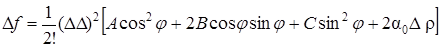
Предположим, что А ¹ 0.

Разделив и умножив на А выражение, стоящее в квадратных скобках, получим

. (49)

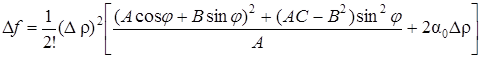
Рассмотрим теперь четыре возможных случая.

1. Пусть АС – В 2 > 0, А 2 ; тогда

,

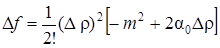
где т не зависит Dr, a₀Dr ® 0 при Dr ® 0. Следовательно, при достаточно малых Dr будет Df 2 > 0, А > 0. Тогда, рассуждая аналогично, получим

,

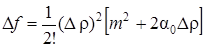
3. Пусть АС – В 2 0. В этом случае функция не имеет ни максимума ни минимума. Функция возрастает, когда мы движемся из точки (х₀, у₀) по одним направлениям, и убывает, когда мы движемся по другим направлениям. Действительно, при перемещении вдоль луча j = 0 имеем

;

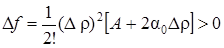
при движении вдоль этого луча функция возрастает. Если же перемещаться вдоль луча j = j₀ такого, что tg j₀ = —А/В, то при А > 0 будет

;

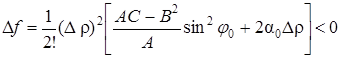
при движении вдоль этого луча функция убывает.

Пусть АС – В 2 2 0 и j 2 2 = 0. В этом случае на основании формул (48) и (49) сделать заключение о знаке Df нельзя. Так, например, при А ¹ 0 будем иметь

;

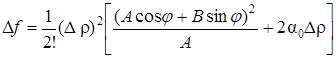
при j = arctg (-А/В) знак Df определяется знаком 2a₀, здесь требуется специальное дальнейшее исследование (например, с помощью формулы Тейлора более высокого порядка или каким-либо иным способом). Таким образом, теорема 2 полностью доказана.

Пример 42. Исследовать на максимум и минимум функцию

.

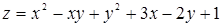
Решение. 1. Находим критические точки:

, .

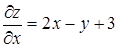
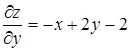
Решая систему уравнений

, .

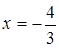
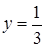
2. Находим производные второго порядка в критической точке (-4/3; 1/3) и определяем характер критической точки:

, , ,

, А > 0.

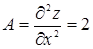
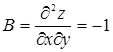
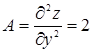
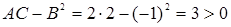
Следовательно, в точке (-4/3; 1/3) данная функция имеет минимум, а именно:

.

Замечание. Теория максимумов и минимумов функции нескольких переменных является основой для одного метода получения формул для изображения функциональных зависимостей на основании экспериментальных данных.

Дата добавления: 2015-07-24 ; просмотров: 1631 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Линии и поверхности уровня

Содержание:

Линии и поверхности уровня

Понятие линии и поверхности уровня:

Для характеристики функций двух переменных вводится понятие линий уровня.

Определение 2. Линией уровня функции z = f (x, y) называется совокупность всех точек на плоскости Oxy, для которых выполняется условие f (x, y) = C.

Линии уровня можно получить, пересекая поверхность z = f (x, y) плоскостями z = C, где С = соnst.

Пример 1. Найти линии уровня функции z = x 2 + y 2 .

Решение.
Пусть z = C. x 2 + y 2 = C (C ≥ 0),

В этом случае линиями уровня является множество концентрических окружностей с центром в начале координат и радиусом С (рис. 2) .Аналогично вводится понятие поверхности уровня для функции трех переменных u = f (x, y, z), (f (x, y, z) = C).

Пример 2. Найти поверхности уровня функции u = x 2 + y 2 + z 2 .

Решение. Пусть u = C. Тогда x 2 + y 2 + z 2 = C (C ≥ 0) — это множество сфер с центром в точке O(0; 0; 0) и радиусом C.

Поверхности второго порядка

Наиболее изучены поверхности в курсе аналитической геометрии — поверхности второго порядка. В общем случае уравнение такой поверхности имеет вид:
a₁₁ x 2 + 2a₁₂ xy + a₂₂ y 2 + 2a₁₃ xz + 2a₂₃ yz + a₃₃ z 2 + 2a₁₄ x + 2a₂₄ y + 2a₃₄ z + a₄₄ = 0.

В зависимости от значений коэффициентов получают различные поверхности второго порядка.

Например:
1) — конус;

2) — полусфера;

Рис. 4.

3) — эллиптический параболоид;

Рис. 5.

4) — гиперболический параболоид;

рис.6

5) — трехосный эллипсоид.

Рис. 7.

Для изучения поверхностей в трехмерном пространстве применяется метод сечений. Суть этого метода такова: пересекаем заданную поверхность плоскостями x = C₁, y = C₂, z = C₃. В результате получим некоторые кривые, характеризующие поверхность.

Пример 3. z = x 2 + y 2 . Пусть z = C₁ (C₁ ≥ 0). Получим уравнение x 2 + y 2 = C₁ (уравнение окружности). Положим y = C₂ , тогда — уравнение параболы в плоскости Оxz, которая смещена на единиц вверх по оси Oz. Положим x = C₃ , получим уравнение
Получили уравнение параболы в плоскости Оyz, которая смещена на единиц вверх по оси Оz. Из этих исследований вытекает, что графиком функции z = x 2 + y 2 является параболоид вращения вокруг оси Оz.

Гиперповерхности уровня

Пусть задана функция от n переменных u = f (x₁, x₂, . x_n) . Если положить u = C, то получим уравнение f (x₁, x₂, . x_n) = C, которое называется уравнением гиперповерхности уровня в пространстве R n . Например: Если u = C, то уравнение является уравнением гиперсферы в R n с центром в точке O (0,0, . 0) и радиусом .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.