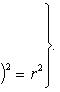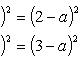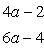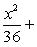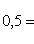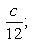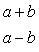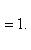Найти уравнение окружности проходящей 3 точки
Написать уравнение окружности, проходящей через три точки: (0, 1); (2, 0); (3, -1).
Искомое уравнение имеет вид (x — a) 2 + (y — b) 2 = r 2 . Поскольку окружность проходит через заданные точки, координаты каждой из этих точек удовлетворяют уравнению окружности. Подставляя поочередно в искомое уравнение координаты данных точек, получим три уравнения для определения a, b и r. Вот эти уравнения:
Возьмем уравнения первое и второе, а потом первое и третье. Правые части этих уравнений между собой равны, значит, равны и левые их части, и мы получаем
Раскрывая скобки и упрощая, будем иметь
Отсюда . Подставляя эти значения a и b в первое из уравнений системы, получим
. Искомое уравнение имеет вид
или после упрощений x 2 + y 2 + 3x + 9y — 10 = 0.
Уравнение окружности, проходящей через три заданные точки
Этот онлайн калькулятор выводит уравнение окружности, проходящей через три заданные точки
Этот онлайн-калькулятор находит окружность, проходящую через три заданные точки. Калькулятор находит центр, радиус и уравнение окружности, и строит окружность на графике. Методы, использованные для нахождения центра и радиуса окружности, описаны ниже под калькулятором.
Уравнение окружности, проходящей через три заданные точки
Первая точка
Вторая точка
Третья точка
Центр
Как найти окружность, проходящюю через три заданные точки
Давайте вспомним как выглядит уравнение окружности в стандартной форме:
Так как все три точки принадлежат одной окружности, мы можем записать систему уравнений
Значения , и мы знаем. Давайте сделаем подстановку с неизвестными переменнами a, b и c.
Теперь у нас есть три линейных уравнения для трех неизвестных — составим систему уравнений соответствующую матричной форме:
Мы можем решить эту систему уравнений, используя, к примеру, Гауссово исключение. (подробнее прочитать об этом можно здесь — Решение системы линейных алгебраических уравнений методом Гаусса ). «Нет решений» — означает, что точки коллинеарны и окружность через них провести нельзя.
Координаты центра окружность и ее радиус относится к подобному решению
Зная центр и радиус, мы можем получить уравнение окружности, используя этот калькулятор — Уравнение окружности по заданному центру и радиусу в различных формах
Задача 30. Написать уравнение окружности, проходящей через три точки: (0, 1); (2, 0); (3, -1).
КРИВЫЕ ВТОРОГО ПОРЯДКА

Окружность.



Для уравнения окружности выполнимо два условия:
1. коэффициенты при x и y равны между собой
2. отсутствует произведение текущих координат вида x*y.
Эллипс.
Эллипс – множество всех точек плоскости, сумма расстояний от каждой из которых до двух фокусов – величина постоянная и большая, чем расстояние между фокусами.

Основные понятия, связанные с уравнением эллипса:
1. Эллипс симметричен относительно координатных осей и относительно начала координат.
2. Точки пересечения с осью Ox 
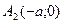

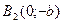
3. Точки 
4. Отрезки 

5. Все точки эллипса лежат внутри прямоугольника, образованного прямыми x = -a, x = a , y = -b, y = b.
6. Если a>b, то эллипс вытянут вдоль оси Ox, а если a 0).

Основные понятия, связанные с уравнением параболы:
1. 

2. Т.к. P>0 , то x 
3. При x =0, y = 0 парабола проходит через начало координат.
4. Точка (0:0) называется вершиной параболы.
Отрезок FM называется фокальным радиусом точки М.
Уравнение 
Задача 30. Написать уравнение окружности, проходящей через три точки: (0, 1); (2, 0); (3, -1).
Решение:
Искомое уравнение имеет вид (x — a) 2 + (y — b) 2 = r 2 . Поскольку окружность проходит через заданные точки, координаты каждой из этих точек удовлетворяют уравнению окружности. Подставляя поочередно в искомое уравнение координаты данных точек, получим три уравнения для определения a, b и r. Вот эти уравнения:

Возьмем уравнения первое и второе, а потом первое и третье. Правые части этих уравнений между собой равны, значит, равны и левые их части, и мы получаем

Раскрывая скобки и упрощая, будем иметь



Подставляя эти значения a и b в первое из уравнений системы, получим
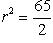
Искомое уравнение имеет вид
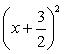
или после упрощений x 2 + y 2 + 3x + 9y — 10 = 0.
Задача 31. Составить простейшее уравнение эллипса, зная, что:
а) его полуоси a = 6, b = 4;
б) расстояние между фокусами 2c = 10, а большая полуось 2a = 16;
в) большая полуось a = 12, а эксцентриситет e = 0,5;
г) малая полуось b = 8, а эксцентриситет e = 0,6;
д) сумма полуосей a + b = 12, а расстояние между фокусами
Решение:
а) Простейшее уравнение эллипса имеет вид


Подставляя сюда a = 6, b = 4, получим
б) Имеем 2c = 10; c = 5; 2a = 16; a = 8.
Чтобы написать уравнение эллипса, следует найти малую полуось b. Между величинами a, b и c у эллипса существует зависимость a 2 — b 2 = c 2 , или b 2 = a 2 — c 2 . В нашем случае b 2 = 64 — 25 = 39, и уравнение эллипса будет иметь вид
в) a = 12; e = 0,5; известно, что 
Теперь, зная, что a = 12, c = 6, пользуясь отношением a 2 — c 2 = b 2 , найдем, что b 2 = 144 — 36 = 108; a 2 = 144.


г) b = 8; e = 0,6; 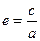


Уравнение эллипса будет иметь вид
д) a + b = 12, 
Для определения уравнения эллипса надо знать a и b. Нам известно, что 
Поэтому (a + b)(a — b) = 18. Подставляя сюда a + b = 12, найдем, что a — b = 1,5.
Решая систему уравнений
получим, что a = 6,75, b = 5,25. Уравнение эллипса запишется в виде

Задача 32. Найти длины осей, координаты фокусов и эксцентриситет эллипса 4x 2 + 9y 2 = 144.
Решение:
Преобразуем это уравнение к простейшему виду


Разделив обе части заданного уравнения на 144, получим
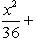
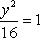
Отсюда заключаем, что a 2 = 36, b 2 = 16. Значит, a = 6, 2a = 12; b = 4, 2b = 8. Зная a и b, из соотношения a 2 — c 2 = b 2 найдем c. Подставим a = 6; b = 4 и получим, что 

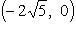
http://planetcalc.ru/8116/
http://poisk-ru.ru/s21192t4.html