Уравнение плоскости, проходящей через точку перпендикулярно вектору
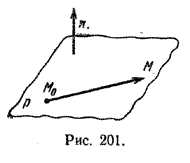
Пусть дана некоторая точка M0 и ненулевой вектор n. Через точку M0 можно провести только одну плоскость р перпендикулярную вектору n (рис. 201).
Выведем уравнение плоскости р. Пусть М — произвольная точка пространства. Очевидно, что точка М принадлежит плоскости р тогда и только тогда, когда вектор \(\overrightarrow
Вектор n в уравнении (1) называется нормальным вектором плоскости. В качестве нормального вектора можно взять любой вектор, перпендикулярный плоскости.
Пусть точка M0 и вектор n заданы своими координатами в некоторой прямоугольной системе координат:
Обозначим координаты произвольной точки М плоскости р через х, у и z. Тогда вектор \(\overrightarrow
Это уравнение называется уравнением плоскости, проходящей через точку (х0; у0; z0) перпендикулярно вектору (А; В; С).
Задача 1. Найти уравнение плоскости, проходящей через точку М0(-3; 4; 7) перпендикулярно вектору n = (1; —2; 6).
В данном случае х0 = -3, у0 = 4, z0 = 7; А = 1, В = -2, С = 6. Подставив эти значения в уравнение (2), получим искомое уравнение
3адачa 2. Даны точки M1 (2; -1; 3) и M2(4; 5; 0). Написать уравнение плоскости, проходящей через точку М2 перпендикулярно вектору \(\overrightarrow
За нормальный вектор плоскости можно взять вектор n = \(\overrightarrow
Задача 3. В треугольнике с вершинами в точках А1<-5; 2; 7), А2(5; 0; 6), А3(0; -1; 2) проведена медиана А1М0. Найти уравнение плоскости, проходящей через точку М0 перпендикулярно медиане А1М0.
За нормальный вектор плоскости можно принять вектор n = \(\overrightarrow
Координаты нормального вектора n = (А; В; С), следовательно, равны
A = 5 /2 + 5 = 15 /2, В = — 1 /2 — 2 = — 5 /2, С = 4 — 7 = — 3.
Уравнения прямой, проходящей через точку коллинеарно вектору
Параметрическое уравнение прямой
Направляющим вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.
Пусть на координатной плоскости заданы точка и ненулевой вектор (рис. 3.13). Требуется составить уравнение прямой, коллинеарной вектору и проходящей через точку .
Выберем на прямой произвольную точку . Обозначим и — радиус-векторы точек и (рис.3.14).
Точка принадлежит заданной прямой тогда и только тогда, когда векторы и коллинеарны. Запишем условие коллинеарности : , где — некоторое действительное число (параметр). Учитывая, что , получим векторное параметрическое уравнение прямой :
где — направляющий вектор прямой, а — радиус-вектор точки, принадлежащей прямой.
Координатная форма записи уравнения (3.11) называется параметрическим уравнением прямой
где — координаты направляющего вектора прямой. Параметр в уравнениях (3.11),(3.12) имеет следующий геометрический смысл : величина пропорциональна расстоянию от начальной точки до точки . Физический смысл параметра в параметрических уравнениях (3.11), (3.12) — это время при равномерном и прямолинейном движении точки по прямой. При точка совпадает с начальной точкой , при возрастании движение происходит в направлении, определяемым направляющим вектором .
Каноническое уравнение прямой
Выразим параметр из каждого уравнения системы (3.12): , а затем исключим этот параметр:
Уравнение (3.13) называется каноническим уравнением прямой . В этом уравнении коэффициенты и не равны нулю одновременно, так как это координаты направляющего вектора прямой.
1. Если один из знаменателей дробей в (3.13) равен нулю, то считается, что соответствующий числитель дроби равен нулю:
– каноническое уравнение – это уравнение прямой , параллельной оси ординат (рис.3.15,а);
– каноническое уравнение — это уравнение прямой , параллельной оси абсцисс (рис.3.15,6).
2. Поскольку направляющий вектор коллинеарен прямой, а нормаль ей перпендикулярна, то векторы и ортогональны. Следовательно, их скалярное произведение равно нулю:
т.е. координаты направляющего вектора прямой и ее нормали связаны однородным уравнением: . Подставим, например, решение этого уравнения в общее уравнение прямой (3.7):
Это соотношение позволяет по координатам направляющего вектора и координатам точки записать уравнение прямой без промежуточных вычислений.
3. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор , где , также является направляющим вектором для той же прямой.
4. Для перехода от общего уравнения прямой (3.8) к каноническому (3.13) нужно выполнить следующие действия:
1) найти любое решение уравнения , определяя тем самым координаты точки , принадлежащей прямой;
2) найти любое ненулевое решение однородного уравнения , определяя тем самым координаты направляющего вектора , в частности, можно взять ;
3) записать каноническое уравнение (3.13).
5. Чтобы перейти от канонического уравнения к общему , достаточно перенести все члены уравнения (3.13) в левую часть:
Полученное уравнение (при ) имеет вид (3.8) с .
6. Чтобы перейти от канонического уравнения к параметрическому , следует приравнять левую и правую части уравнения (3.13) параметру и записать полученное двойное равенство в виде системы (3.12):
7. Параметрическое (3.12) и каноническое (3.13) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.
Пример 3.8. На координатной плоскости (в прямоугольной системе координат) заданы прямая и точка (рис.3.16). Требуется:
а) Нормаль к прямой является направляющим вектором для прямой . Координаты нормали определяем по общему уравнению прямой , тогда , . Составляем параметрическое уравнение (3.12) прямой :
б) Проекция точки является точкой пересечения прямых и . Найдем ее координаты. Для этого подставляем в уравнение прямой выражения координат и из параметрического уравнения прямой . Получим уравнение
Значению параметра отвечает точка с координатами и . Следовательно, искомая точка .
в) В пункте «а» составлено параметрическое уравнение прямой . В этом уравнении при получаем точку , при — точку , значит искомую точку получим при , поскольку в силу симметрии . Вычисляем координаты искомой точки:
Пример 3.9. На координатной плоскости (в прямоугольной системе координат) заданы вершины треугольника (рис.3.17). Составить:
а) каноническое уравнение прямой, содержащей высоту треугольника;
б) каноническое и параметрическое уравнения прямой, содержащей биссектрису треугольника.
а) В примере 3.7 было получено общее уравнение прямой . Перейдем от общего уравнения к каноническому.
1) Найдем любое решение уравнения , например, и (точкам принадлежит прямой ).
2) Найдем ненулевое решение однородного уравнения , например (направляющий вектор прямой имеет координаты ).
3) Запишем каноническое уравнение: .
б) Найдем направляющий вектор биссектрисы . Для этого отложим от вершины единичные векторы и построим на них ромб (изображенный на рис.3.17 штриховой линией). Поскольку диагональ ромба является биссектрисой, то вектор . является направляющим вектором биссектрисы . Находим координаты и длины векторов:
Составляем каноническое уравнение прямой с направляющим вектором , проходящей через точку :
Чтобы получить параметрическое уравнение прямой , приравниваем левую и правую части канонического уравнения параметру . Записываем полученную систему в виде
Уравнение плоскости, проходящей через точку и прямую онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:
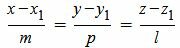 . . | (1) |
Задача заключается в построении уравнения плоскости α, проходящей через точку M0 и и через прямую L(Рис.1).
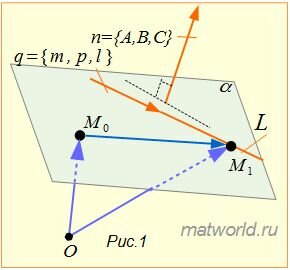 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (3) |
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (5) |
Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M0 и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:
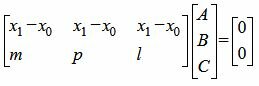 . . | (6) |
Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.
Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.
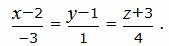 | (7) |
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0)=M0(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (8) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
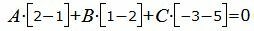 | (10) |
 | (11) |
Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
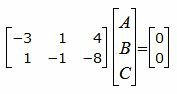 | (12) |
Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:
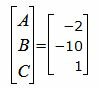 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:
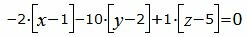 | (13) |
Упростим уравнение (13):
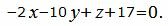 | (14) |
Ответ: Уравнение плоскости, проходящей через точку M0(1, 2, 5) и через прямую (7) имеет вид (14).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и через прямую L, заданной параметрическим уравнением:
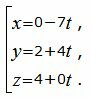 | (15) |
Решение. Приведем параметрическое уравнение (15) к каноническому виду:
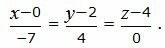 | (16) |
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (17) |
Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (18) |
Вычитая уравнение (18) из уравнения (17), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (19) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :
| Am+Bp+Cl=0. | (20) |
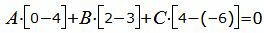 | (21) |
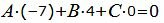 | (22) |
Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
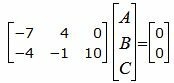 | (23) |
Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:
 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:
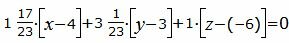 | (24) |
Упростим уравнение (24):
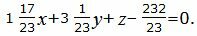 | (25) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.
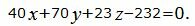 | (26) |
Ответ: Уравнение плоскости, проходящей через точку M0(4, 3, −6) и через прямую (16) имеет вид (26).
http://mathhelpplanet.com/static.php?p=uravneniya-pryamoi-kollinyearno-vektoru
http://matworld.ru/analytic-geometry/uravnenie-ploskosti4-online.php