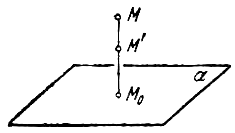
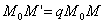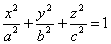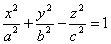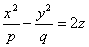Найти уравнение прямого кругового цилиндра проходящего через точку

Найти уравнение прямого кругового цилиндра проходящего через точку

Глава 46. Поверхности второго порядка

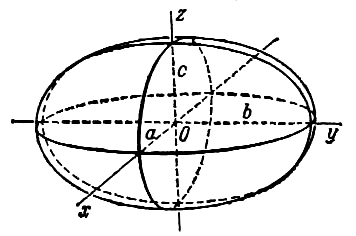
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

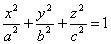
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

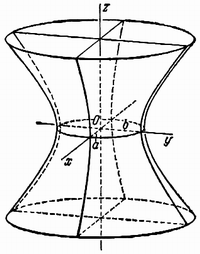
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

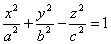
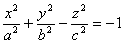
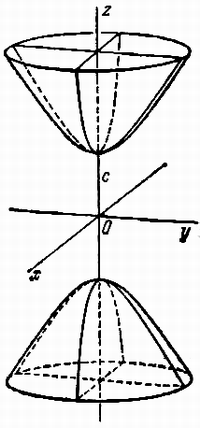
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

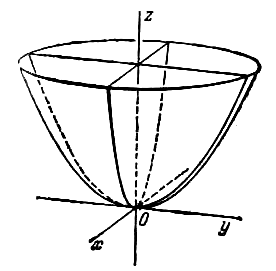
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

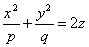
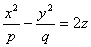
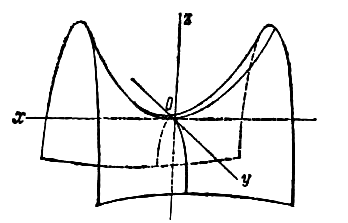
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

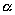
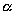
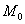
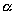
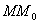
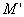
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

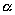
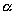
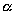
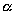
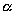
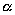
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .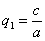

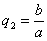
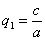
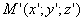
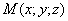
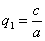
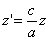
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

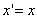
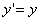
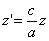
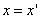
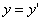
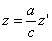
Предположим, что M(x; y; z ) — произвольная точка сферы

.

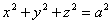
Заменим здесь x, y, z их выражениями (7); получим

,

.

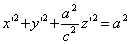
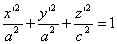
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

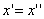
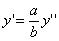
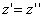
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

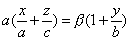
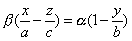
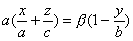
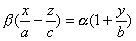
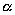
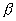
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

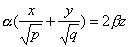
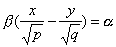
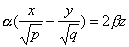
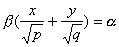
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

Цилиндрические поверхности

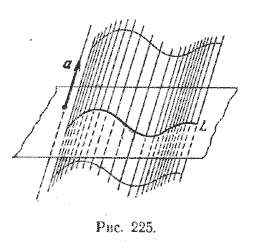
Если через каждую точку кривой L провести прямую, параллельно данному вектору а, то получим поверхность, которая называется цилиндрической поверхностью. Прямые, параллельные вектору а и принадлежащие цилиндрической поверхности, называются образующими этой поверхности, а кривая L называется направляющей цилиндрической поверхности (рис. 225).

Если в сечении цилиндрической поверхности плоскостью, перпендикулярной к ее образующим, (в нормальном сечении) получается окружность, то цилиндрическая поверхность называется круговой. Если в сечении получается эллипс, то цилиндрическую поверхность называют эллиптической, если гипербола — гиперболической, если парабола — параболической.

Пусть в пространстве дана прямоугольная система координат Oxyz, и пусть в плоскости хОу дана кривая L, уравнение которой в этой плоскости имеет вид

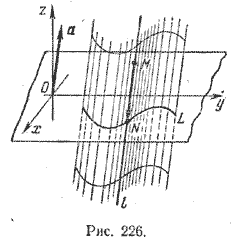
Составим уравнение цилиндрической поверхности с образующими, параллельными вектору a = (α; β; γ), γ =/= 0, если за направляющую принята кривая L (рис.226).

Рассмотрим произвольную точку этой поверхности М(х; у; z). Образующая l, проходящая через точку М, пересечет плоскость хОу в точке N, лежащей на кривой L. Если координаты точки N в пространстве обозначить (х₁; у₁; 0), то вектор \(\overrightarrow\) имеет координаты

По определению цилиндрической поверхности векторы а и \(\overrightarrow\) коллинеарны, т. е.

следовательно, имеем систему уравнений

Решив эту систему уравнений относительно λ, x₁и у₁, получим

Так как точка N лежит на кривой L, то F(х₁; у₁) = 0. Заменив х₁ и у₁ по формулам (2), получим уравнение

которое, очевидно, и будет уравнением данной цилиндрической поверхности.

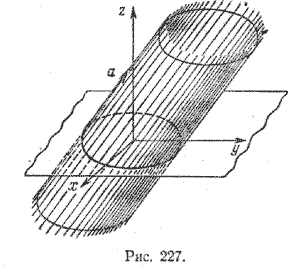
Задача 1. Составить уравнение цилиндрической поверхности, у которой направляющая лежит в плоскости хОу и имеет уравнение х 2 + у 2 = 4, а образующие параллельны вектору а = (0; 1; 1).

Так как, согласно условию задачи F(x; у) = х 2 + у 2 — 4 и α = 0, β = 1, γ = 1, то в силу формулы (3) уравнение данной цилиндрической поверхности имеет вид

Эта поверхность изображена на рис. 227.

Аналогично можно показать, что если направляющая цилиндрической поверхности L лежит в плоскости xOz и определяется уравнением F(x; z) = 0, а вектор а не параллелен этой плоскости, то цилиндрическая поверхность имеет уравнение

Наконец, если L определяется уравнением F(у; z) = 0 и а не параллелен плоскости yOz, то уравнение цилиндрической поверхности имеет вид

Отметим, что если направляющая цилиндрической поверхности лежит в плоскости

хОу, а образующие параллельны оси Oz, то уравнение цилиндрической поверхности в пространстве совпадает с уравнением направляющей и имеет вид

Уравнение (4), как уравнение множества точек плоскости, определяет кривую L, в то же самое время уравнение (4), как уравнение множества точек пространства, определяет цилиндрическую поверхность.

Итак, каждое из уравнений

можно истолковать двояко: если это уравнение множества точек плоскости, то это уравнение линии L, лежащей в плоскости своих переменных; если же это уравнение множества точек пространства, то каждое из этих уравнений определяет цилиндрическую поверхность с направляющей L и образующими, параллельными оси oтсутствующей переменной.

Рассмотрим несколько примеров.

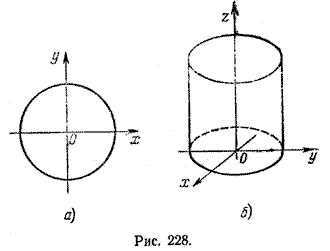
на плоскости хОу определяет окружность с центром в начале координат и радиусом r (рис. 228, а).

Это жe уравнение в пространстве определяет круговую цилиндрическую поверхность, направляющей которой является окружность, лежащая в плоскости хОу, а образующие параллельны оси Oz (рис. 228, б).

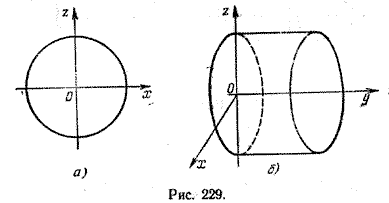
на плоскости xOz определяет окружность с центром в начале координат и радиусом

Это же уравнение в пространстве определяет круговую цилиндрическую поверхность, направляющей которой является окружность, лежащая в плоскости xOz, а образующие параллельны оси Оу (рис. 229, б).

и на плоскости, и в пространстве определяет пустое множество, так как сумма неотрицательных чисел не может быть числом отрицательным.

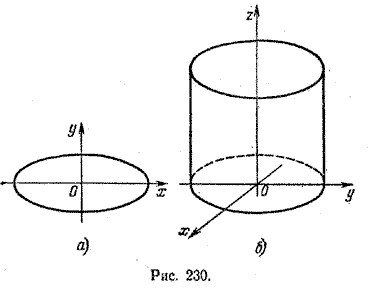
на плоскости хОу определяет эллипс с центром в начале координат и полуосями а и b (рис. 230, а).

Это же уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости хОу и образующими, параллельными оси Oz (рис. 230, б).

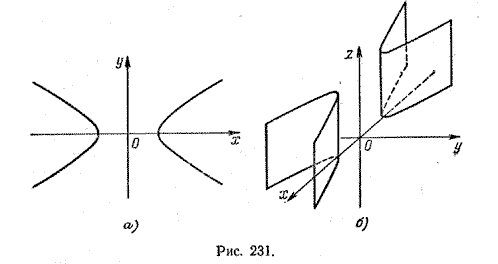
на плоскости хОу определяет гиперболу с центром в начале координат и полуосями а и b (рис. 231, а).

В пространстве это уравнение определяет гиперболическую цилиндрическую поверхность с образующими, параллельными оси Oz (рис. 231, б).

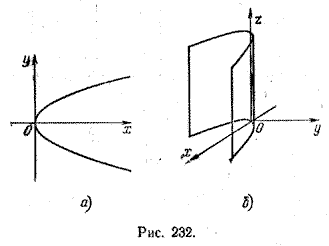
на плоскости хОу определяет параболу (рис. 232, а), а в пространстве — параболическую цилиндрическую поверхность с образующими, параллельными оси Oz (рис. 232, б).

Задача 2. Определить вид поверхности 3x 2 + 6y 2 — 24 = 0.

Данное уравнение приведем к виду:

Это уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости хОу и образующими, параллельными оси Oz.