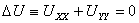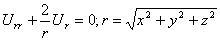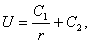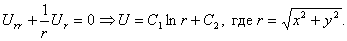Найти уравнение пуассона в круге радиуса r

Уравнение Пуассона и математическая постановка задач электростатики

Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:

где ρ является плотностью распределения заряда, ε 0 — электрической постоянной, d i v E → = ∇ → E → = ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.

Произведем подстановку ( 2 ) в ( 1 ) :

Учитывая, что d i v g r a d φ = ∇ 2 φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ z 2 , где ∆ = ∇ 2 — это оператор Лапласа, равенство ( 3 ) принимает вид:

Выражение ( 4 ) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:

После нахождения потенциала переходим к вычислению напряженности, используя ( 2 ) . Решения уравнения Пуассона должны удовлетворять требованиям:

• значение потенциала как непрерывная функция;
• потенциал должен быть конечной функцией;
• производные потенциала как функции по координатам должны быть конечными.

При наличии сосредоточенных зарядов в объеме V , решение уравнения ( 4 ) будет выражаться для потенциала вида:

Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ , удовлетворяющую условиям, то она является единственным решением.

В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.

Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:

E 2 n — E 1 n = 4 π σ , или ∂ φ 1 ∂ n — ∂ φ 2 ∂ n = 0 .

где σ — это поверхностная полость свободных зарядов, n – единичный вектор нормали к границе раздела, проведенный из среды 1 в 2 , τ — единичный вектор, касательный к границе.

Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.

Уравнение Пуассона в сферических, полярных и цилиндрических координатах

Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.

При наличии сферических r , θ , υ уравнение Пуассона запишется как:

1 r 2 · ∂ ∂ r r 2 ∂ φ ∂ r + 1 r 2 sin θ ∂ θ sin θ · ∂ φ ∂ θ + ∂ 2 φ r 2 sin 2 θ ∂ φ 2 = — 1 ε 0 ρ .

В полярных r , θ :

1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ r 2 ∂ θ 2 = — 1 ε 0 ρ .

В цилиндрических r , υ , z :

1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ ∂ z 2 + ∂ 2 φ r 2 ∂ υ 2 = — 1 ε 0 ρ .

Примеры решения задач

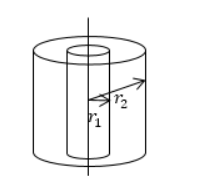
Найти поле между коаксиальными цилиндрами с радиусами r 1 и r 2 и с имеющейся разностью потенциалов ∆ U = φ 1 — φ 2 .

Решение

Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:

1 r · ∂ ∂ r r ∂ φ ∂ r = 0 .

Решение имеет вид φ = — A ln ( r ) + B . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:

φ ( r 2 ) = 0 = — A ln r 2 + B , следовательно

φ ( r 1 ) = ∆ U = — A ln r 1 + B , получим:

A = ∆ U ln r 2 r 1 .

φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .

Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .

Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом R и объемной плотностью заряда ρ . Использовать уравнение Пуассона.

Решение

Необходимо направить ось Z по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией φ ( r ) с r , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:

φ 2 = C 2 ln r + C ‘ 2 .

C 1 , C ‘ 1 , C 2 , C ‘ 2 — это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а l i m r → 0 ln r = ∞ . Отсюда следует, что C 1 = 0 . Далее необходимо пронормировать потенциал, задействовав условие φ 1 ( 0 ) = 0 . Получим C ‘ 1 = 0 .

Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при r = R , как и сам потенциал. Исходя из условий, можно найти C 2 , C ‘ 2 :

C 2 ln R + C ‘ 2 = — 1 4 ρ ε 0 R 2 .

C 2 R = — 1 2 ρ ε 0 R .

Значит, полученные выражения записываются как:

Ответ: потенциал поля равняется:

Уравнение Пуассона и математическая постановка задач электростатики

Вы будете перенаправлены на Автор24

Решение уравнения Пуассона

В достаточно большом количестве случаев наиболее удобным методом поиска напряженности поля является решение дифференциального уравнения для потенциала. Получим его, используя в качестве основы теорему Остроградского — Гаусса в дифференциальной форме:

где $\rho $ — плотность распределения заряда, $<\varepsilon >_0$ — электрическая постоянная, $div\overrightarrow=\overrightarrow<\nabla >\overrightarrow=\frac<\partial E_x><\partial x>+\frac<\partial E_y><\partial y>+\frac<\partial E_z><\partial z>$) — дивергенция вектора напряженности и выражение связывающее напряженность поля и потенциал:

Подставим (2) в (1), получим:

Учитываем, что $divgrad\varphi =<\nabla >^2\varphi =\frac<<\partial >^2\varphi ><\partial x^2>+\frac<<\partial >^2\varphi ><\partial y^2>+\frac<<\partial >^2\varphi ><\partial z^2>$, где $\triangle =<\nabla >^2$- оператор Лапласа, тогда равенство (3) запишем как:

Уравнение (4) называется уравнением Пуассона (для вакуума) в системе СИ. Если заряды отсутствуют, то уравнение (4) преобразуется в уравнение Лапласа:

После того, как найден потенциал из уравнения Пуассона, обычно вычисляется напряженность по формуле (2). Решения уравнения Пуассона должны удовлетворять таким требованиям:

1. Потенциал должен быть непрерывной функцией.
2. Потенциал должен быть конечной функцией.
3. Производные от потенциала как функции по координатам должны быть конечными.

Если заряды сосредоточены в объеме V, то решением уравнения (4) будет выражение для потенциала вида:

Итак, общая задача электростатики сводится к нахождению решения дифференциального уравнения (уравнения Пуассона), которое удовлетворяет выше перечисленным требованиям. Нахождение решения — задача весьма сложная. Теоретические решения известны для небольшого количества частных случаев. Если удалось подобрать функцию $\varphi $, которая удовлетворяет всем условиям задачи, то она единственная.

Готовые работы на аналогичную тему

Не всегда есть необходимости задавать заряды или потенциалы во всем пространстве. Например, если необходимо найти электрическое поле в полости, которая окружена проводящей оболочкой, то можно найти поле только для тел внутри самой полости.

Каждое решение уравнения Пуассона в ограниченной области однозначно определяется краевыми условиями, которые накладывают на поведение решения. На границе перехода из одной среды в другую выполняются граничные условия:

где $\sigma $- поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 1 в 2, $\tau -\ $единичный вектор, касательный к границе.

Данные уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной составляющей вектора напряженностей электрического поля при переходе через любую заряженную поверхность не зависимо от формы этой поверхности и наличия и отсутствия зарядов вне ее.

Уравнение Пуассона в сферических, полярных и цилиндрических координатах

Уравнение Пуассона может быть записано не только в декартовых координатах, но также в сферических и цилиндрических, полярных.

В сферических координатах ($r,\theta ,\vartheta)$ уравнение Пуассона имеет следующий вид:

В полярных координатах ($r,\theta )$ система координат уравнение имеет вид:

В цилиндрических координатах ($r,\vartheta,z)$ уравнение имеет вид:

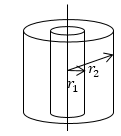
Задание: Найдите поле между двумя коаксиальными цилиндрами с радиусами $r_1$ и $r_2$, разность потенциалов между которыми равна $\triangle U=<\varphi >_1-<\varphi >_2.$

Запишем уравнение Лапласа в цилиндрических координатах с учетом аксиальной симметрии:

Оно имеет решение $\varphi =-Aln(r)$+B. Выберем нулевой потенциал на наружном цилиндре, найдем, получим:

$\varphi \left(r_2\right)=0=-Alnr_2+B,$ следовательно

Ответ: Поле между двумя коаксиальными цилиндрами задается функцией $\varphi (r)=-\frac<\triangle U><\right)\ >>ln\left(r\right)+\frac<\triangle U><\right)\ >>lnr_2$

Задание: Найти, используя уравнение Пуассона потенциал поля, которое создает бесконечно длинный круглый цилиндр радиуса R с объемной плотностью заряда $\rho $.

Ось Z направим по оси цилиндра. Так как цилиндрическое распределение заряда аксиально симметрично, то потенциал обладает той же симметрией, то есть он является функцией $\varphi \left(r\right),\ $где r — расстояние от оси цилиндра. Поэтому используем цилиндрическую систему координат. Запишем уравнение Пуассона в ней с учетом симметрии:

где $C_1$,$\ _1,C_2$,$\ _2$ — постоянные интегрирования. Так как потенциал во всех точках должен быть конечным, а $<\mathop_ lnr\ >=\infty $, следовательно, $C_1=0.$ Пронормируем потенциал условием:$<\varphi >_1\left(0\right)=0$, тогда: $_1=0.$

Так как поверхностных зарядов нет, то напряженность электрического поля на поверхности шара непрерывна, то есть непрерывна производная от потенциала при r=R. И непрерывен сам потенциал. Эти условия дают два алгебраических уравнения для того, чтобы найти постоянные $C_2$,$\ _2:$

Следовательно, получаем выражения для потенциалов:

\[<\varphi >_1\left(r\right)=-\frac<1><4>\frac<\rho ><<\varepsilon >_0> r ^ 2 \left(0 Ответ: Потенциал поля равен: $$ \varphi_1 \left(r \right)=-\frac<1><4>\frac<\rho > <\varepsilon_0>r^2 \left (0

Лекция 7. Гармонические функции и их свойства

Рассмотрим уравнение Лапласа на плоскости

и в пространстве

Уравнение (33) при переходе к полярным координатам преобразуется к виду

Рис 14 Рис 14.1

Если в пространстве перейти к сферическим координатам

то уравнение (34) примет вид

Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (33) или (34) в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве. Особый интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных — круговой) симметрией.

Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения

Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим

где C₁ и C₂ — произвольные постоянные. Полагая C₁=1, C₂=0, получим функцию

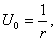
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U₀ является гармонической всюду в пространстве, кроме начала координат 0.

Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:

Выбирая С₁=-1 и С₂=0, будем иметь функцию

Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины q , помещенным в начало координат. Тогда потенциал этого поля равен

Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен

где q₁ — линейная плотность заряда (то есть заряд, рассчитанный на единицу длины).

Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.

Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (х_o,у_o) и непрерывная в соответствующем замкнутом круге Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть

При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)

Если в этой формуле положить ρ=0, то получится формула (35).

Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где 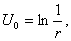(см. рис.15.1):

Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:

где D — круг радиуса R. Разделив обе части полученного равенства на R 2 /2 , будем иметь

В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.

Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (х_о, у_о), то эта функция гармоническая в D. Из формулы (37) получается:

Следствие. Если функция U=U(x,y) гармоническая в некотором круге D радиуса R и непрерывная в соответствующем замкнутом круге ,то

Число называют нормой функции U=U(x,y) в области D , и неравенство (38) можно переписать в виде

Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:

Применим это неравенство к формуле (37):

Что и требовалось доказать.

Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.

Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (x_o, у_o) и непрерывная в соответствующем круге Тогда при любом она удовлетворяет неравенству

Из неравенства Харнака следует теорема Лиувилля.

Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.

Доказательство. Если функция U=U(x, у) ограничена сверху, то U₁=-U(x, y) — ограничена снизу и тоже гармоническая. Поэтому достаточно рассмотреть случай, когда функция ограничена снизу: Более того, можно считать, что M=0. Действительно, ,а разность (U-M) тоже гармоническая функция. Итак, предполагая существование гармонической во всей плоскости неотрицательной функции U(x, у), мы докажем, что эта функция постоянная.

Воспользуемся неравенством Харнака

Если функция U(x, у) гармоническая во всей плоскости то, фиксировав произвольное и неограниченно увеличивая R мы получим

то есть Теорема Лиувилля доказана.

Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.

Терема о среднем. Пусть функция U=U(x, у) гармоническая в некотором шаре D радиуса R c центром
(x_o , у_o , z_o ) и непрерывная в соответствующем замкнутом шаре Тогда значение этой функции в центре шара равно:

а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть

б) ее среднему значению в шаре D, то есть