Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
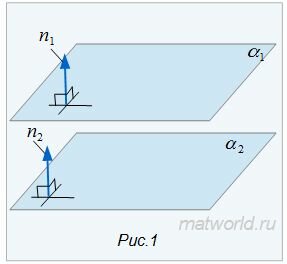
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
 |
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
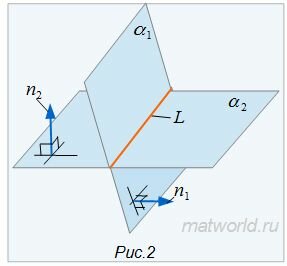 |
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
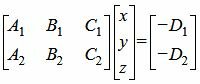 | (4) |
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=<A1, B1, C1> и n2=<A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
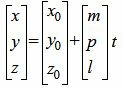 , , | (5) |
Равенство (5) можно записать в следующем виде:
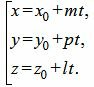 . . | (6) |
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
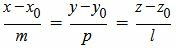 . . |
Пример 1. Найти линию пересечения плоскостей α1 и α2:
| α1: x+2y+z+54=0. | (7) |
| α2: 2x+9y−5z+32=0. | (8) |
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
 . . | (9) |
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 . . | (10) |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
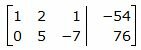 . . |
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
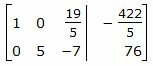 . . |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 . . |
 . . | (11) |
где t− произвольное действительное число.
Запишем (11) в следующем виде:
 . . | (12) |
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
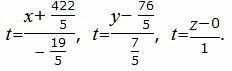 | (13) |
Из равентсв выше получим каноническое уравнение прямой:
 |
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
 |
Пример 2. Найти линию пересечения плоскостей α1 и α2:
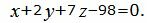 | (14) |
 | (15) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
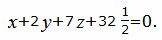 | (16) |
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
 | (17) |
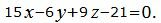 | (18) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
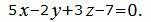 | (19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Проекция линии пересечения двух поверхностей на координатную плоскость
§20. Проекция линии пересечения двух поверхностей на координатную плоскость.
Одной из важнейших задач исследования взаимного расположения двух поверхностей является определение линии их пересечения. Формально, линия пересечения записывается как система двух уравнений с тремя переменными (см. §12 и §16): 
значение z * , при котором точка (x * ,y * , z * ) принадлежит линии пересечения поверхностей. Следовательно, прямая параллельная оси OZ, проходящая через точку линии пересечения поверхностей, на плоскости XOY пересекает кривую f(x,y) = 0. Множество таких прямых образуют цилиндр с направляющей f(x,y) = 0 в плоскости XOY и образующей параллельной оси OZ (§18). Таким образом, доказано следующее утверждение:
Если исключить одну из переменных из уравнений двух поверхностей, то получится уравнение проекции линии пересечения этих поверхностей на координатную плоскость двух оставшихся переменных.
Пример. Найти проекцию линии пересечения поверхностей 

плоскость YOZ. <Исключим х: 


Пересечение поверхностей и способы построения линий пресечения
Пересечение поверхностей и способы построения линий пресечения
Линия пересечения принадлежит обеим пересекающимся поверхностям и образуется множеством их общих точек. Следовательно, построение линии пересечения поверхностей сводится к построению этих общих точек.
При пересечении поверхностей вращения порядок линии пересечения определяется умножением порядков пересекающихся поверхностей. Например, если пересекаются круговой конус (поверхность 2-го порядка) и сфера (поверхность 2-го порядка), то линия пересечения является кривой 4-го порядка.
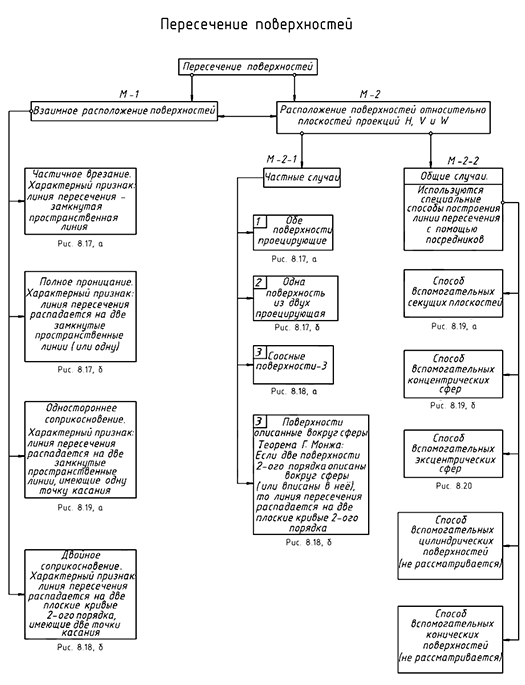
Определение способа построения линии пересечения зависит от взаимного расположения пересекающихся поверхностей, а также от их расположения относительно плоскостей проекций.
Из всех возможных
вариантов пересечения поверхностей геометрических тел в зависимости от их взаимного расположения можно выделить четыре случая, которые позволяют определить и представить форму линии пересечения поверхностей:
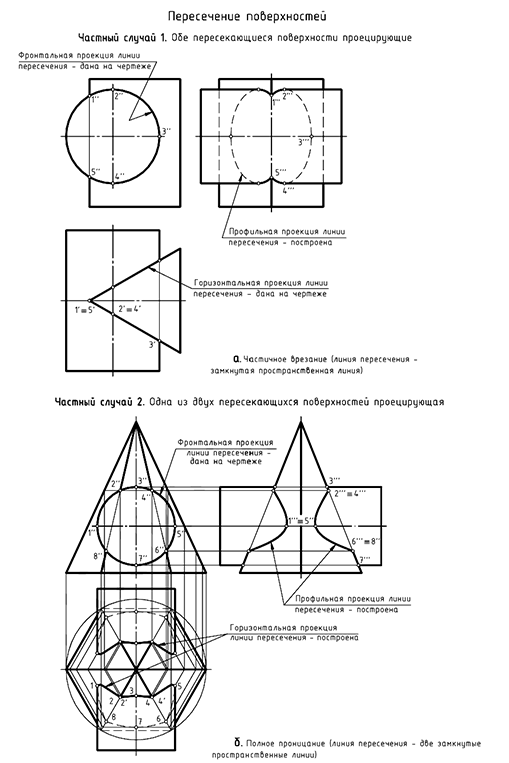
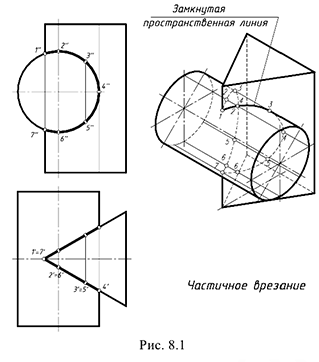
I случай. Частичное врезание (рис. 8.1). В этом случае линией пересечения является одна замкнутая пространственная линия.
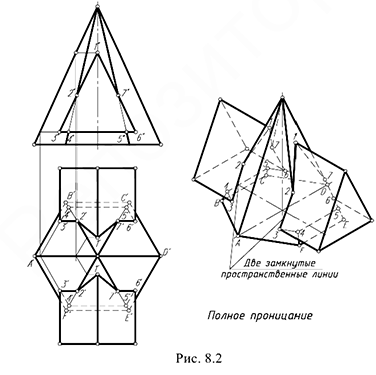
II случай. Полное проницание (рис. 8.2). В этом случае линией пересечения являются две замкнутые пространственные линии.
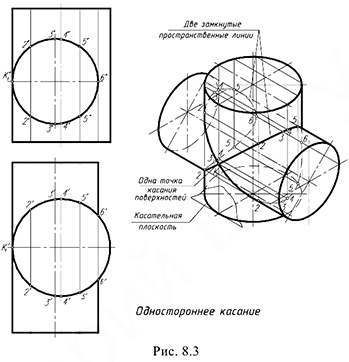
III случай. Одностороннее соприкосновение (рис. 8.3). В этом случае поверхности соприкасаются в одной общей точке 
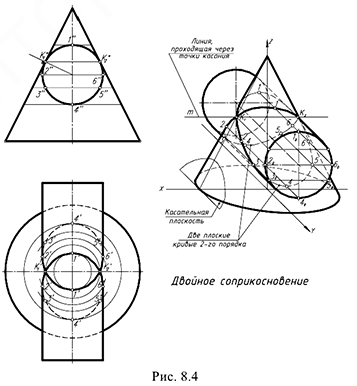
IV случай. Двойное соприкосновение (рис. 8.4).
В этом случае поверхности имеют две точки соприкосновения 
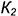
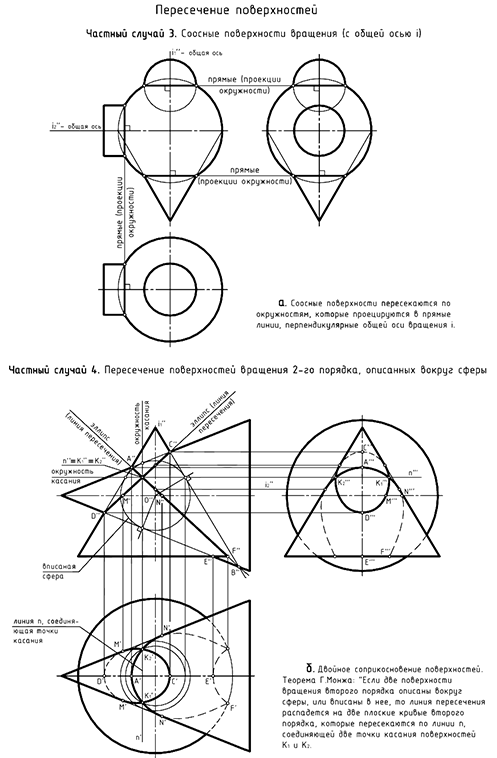
«Если две поверхности вращения второго порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую /77, соединяющую точки касания» (поверхности имеют две общие касательные плоскости).
В зависимости от расположения пересекающихся геометрических тел относительно плоскостей проекции и участия в пересечении геометрических тел, имеющих проецирующую поверхность (как призма или цилиндр) или не имеющих проецирующей поверхности (пирамида, конус, шар, тор, тороид, наклонная призма или наклонный цилиндр, глобоид и др.), следует выбрать оптимальный способ построения проекций линии пересечения поверхностей на чертеже.
По этим признакам способы построения линий пересечения поверхностей можно объединить в две группы:
Первая группа: частные случаи пересечения поверхностей, когда для построения линий пересечения не требуется применения специальных способов, а используется частное положение пересекающихся геометрических тел относительно плоскостей проекций.
Вторая группа: общие случаи пересечения поверхностей, когда для построения линий пересечения требуется применить специальные способы посредников.
Частные случаи пересечения поверхностей
К первой группе частных случаев пересечения поверхностей относятся следующих четыре случая:
1 случай: пересечение геометрических тел, боковые поверхности которых являются проецирующими, то есть, перпендикулярны какой-либо плоскости проекций.
2 случай: пересечение геометрических тел, у одного из которых боковая поверхность является проецирующей.
3 случай: пересечение соосных поверхностей вращения, т. е. имеющих общую ось вращения,
4 случай: пересечение поверхностей вращения второго порядка, описанных вокруг сферы (по теореме Г. Монжа).
Рассмотрим на примерах построение проекций линий пересечения поверхностей геометрических тел в четырех частных случаях первой группы.
Следует отметить, что перечисленные частные случаи пересечения поверхностей наиболее часто встречаются при формообразовании различных реальных деталей.
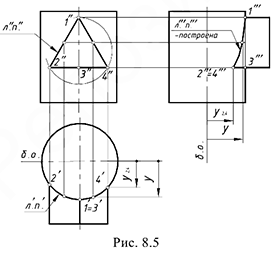
1-й частный случай. На рис. 8.5 показан пример построения проекций линии пересечения поверхностей горизонтально-проецирующего цилиндра и фронтально-проецирующей прямой правильной треугольной призмы, то есть пересекаются два геометрических тела, боковые поверхности которых занимают относительно плоскостей проекций проецирующее положение.
Характерный признак 1-го частного случая: на заданных проекциях тел определяются две проекции искомой линии пересечения:
-фронтальная проекция 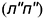
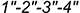
-горизонтальная проекция 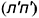
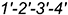
Следовательно, требуется достроить только профильную проекцию 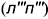
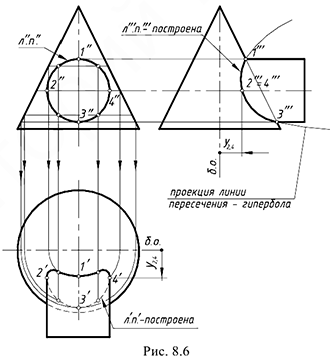
На рис. 8.6 показан пример построения проекций линии пересечения поверхностей прямого кругового конуса и фронтально-проецирующего цилиндра, то есть пересекающихся геометрических тел, у одного из которых боковая поверхность проецирующая.
Характерный признак 2-го частного случая: на заданных проекциях тел определяется одна проекция линии пересечения:
- фронтальная проекция
линии пересечения
совпадает с окружностью, которая является вырожденной проекцией боковой поверхности цилиндра.
Следовательно, требуется достроить горизонтальную 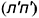
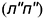
. На профильную проекцию предмета пространственная кривая линия пересечения 4-го порядка проецируется в виде участка гиперболы.
3-й частный случай.
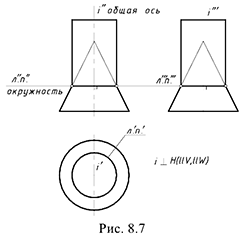
Пересечение соосных геометрических тел
Соосными называются геометрические тела вращения, имеющие общую ось вращения «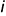
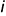
На рис. 8.7 показан пример построения линии пересечения соосных геометрических тел — конуса и горизонтально-проецирующего цилиндра, имеющих общую горизонтально-проецирующую ось 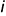
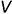
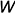
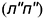
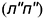
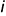
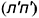
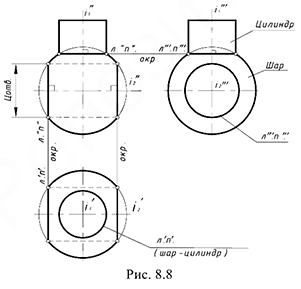
На рис. 8.8 показан пример цилиндр построения линий пересечения двух пар соосных поверхностей:
- поверхности шара и горизонтально-проецирующего цилиндра, соосных относительно горизонтапьно-проецирую-щей оси
, окружности пересечения которых проецируются в прямые линии на фронтальную и профильную проекции;
- поверхности шара и сквозного профильно-проецирующего цилиндрического отверстия
в шаре, соосных относительно профильно-проецирующей оси
, окружности пересечения которых проецируются в прямые линии на фронтальную и горизонтальную проекции.
4-й частный случай.
Пересечение поверхностей вращения второго порядка, описанных вокруг сферы (по теореме Г. Монжа).
Напоминаем, к поверхностям вращения второго порядка относятся круговые цилиндр и конус, шар, эллипсоиды, параболоид и одно-, двуполостные гиперболоиды.
Эллиптические цилиндры и конусы, а также наклонный круговой конус — это не поверхности вращения!
Все торы (открытый, закрытый и самопересекающийся), глобоиды и тороиды относятся к поверхностям вращения четвертого порядка!
В 4-м частном случае имеет место двойное соприкосновение пересекающихся поверхностей вращения второго порядка, описанных вокруг сферы, и построение линии пересечения основано на теореме 2 (С. А. Фролов «Начертательная геометрия» [23]):
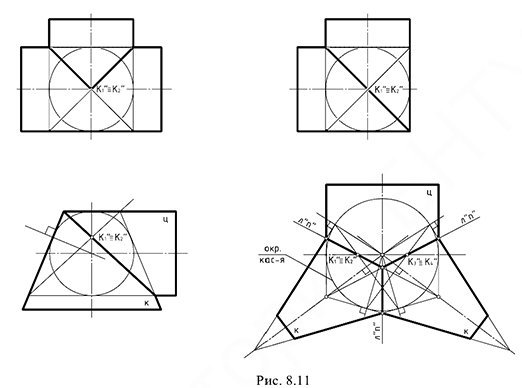
Теорема 3, известная как теорема Г. Монжа, вытекает из теоремы 2: «Если две поверхности вращения второго порядка описаны вокруг третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания».
Практическое применение теоремы возможно в том случае, когда две поверхности вращения второго порядка описаны вокруг сферы или вписаны в нее.
Использовать теорему Г. Монжа для построения на чертеже линии пересечения поверхностей можно при наличии в задаче четырех обязательных графических условий:
- Пересекаются поверхности вращения второго порядка.
- Оси поверхностей вращения должны пересекаться (точка пересечения — центр вписанной сферы).
- Поверхности описаны вокруг общей сферы или вписаны в нее.
- Общая плоскость симметрии, проходящая через оси поверхностей, является плоскостью уровня.
При соблюдении этих четырех условий на одной из заданных проекций можно построить проекции двух плоских кривых, на которые распадается искомая линия пересечения:
- плоские кривые проецируются в отрезки прямых линий на ту проекцию предмета, которая расположена на плоскости проекций, параллельной общей плоскости симметрии поверхностей;
-точки пересечения очерков поверхностей на этой проекции принадлежат искомой линии пересечения и через эти точки проходят прямые, в которые проецируются плоские кривые пресечения;
- прямые, как проекции плоских кривых, пересекаются в точке, с которой совпадают проекции двух точек
соприкосновения поверхностей и соответственно проекция прямой
, соединяющей эти точки соприкосновения (точки касания).
. Точки касания (соприкосновения) поверхностей 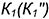
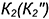
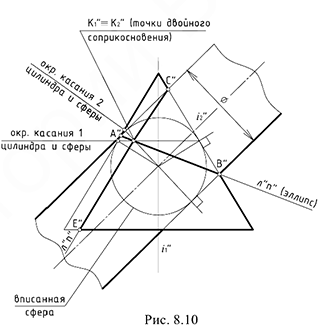
На рис. 8.9 показан пример построения проекций линии пересечения поверхностей вращения второго порядка — прямого кругового конуса и наклонного кругового цилиндра, описанных вокруг общей сферы. Для решения задачи использована теорема Г. Монжа, поскольку здесь соблюдены все четыре обязательных условия ее применения:
- Пересекаются прямой круговой конус и круговой наклонный цилиндр, т. е. поверхности вращения второго порядка.
- Оси конуса и цилиндра пересекаются в точке
.
- Обе поверхности описаны вокруг общей для них сферы с центром точке
.
- Общая плоскость симметрии поверхностей а(ан) является фронтальной плоскостью уровня
.
Построение проекций линии пересечения поверхностей по теореме Г. Монжа выполняется по следующему графическому алгоритму:
1-е действие. Определить проекцию предмета, на которую плоские кривые проецируются в отрезки прямых линий: в данной задаче это фронтальная проекция, так как общая плоскость симметрии 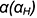
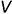
2-е действие. Построить фронтальные совпадающие проекции 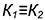
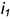
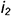
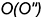
3-е действие. Отметить на фронтальной проекции точки 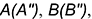
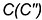
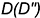
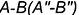
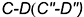
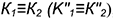
4-е действие. Построить горизонтальные проекции двух плоских кривых пересечения — эллипсов, по горизонтальным проекциях обозначенных точек 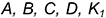
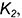
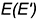
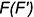
5-е действие. Оформить фронтальный и горизонтальный очерки пресекающихся поверхностей.
. Построение точек соприкосновения 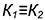
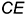
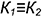
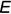
На рис. 8.11 показаны примеры построения линий пересечения поверхностей второго порядка, описанных вокруг сферы, с применением теоремы Г. Монжа. Они часто встречаются при конструировании различных переходов цилиндрических и конических труб, или пересечений отверстий в деталях.
Общие случаи пересечения поверхностей и способы построения линий пересечения поверхностей
Ко второй рассматриваемой группе относятся общие случаи пересечения геометрических тел, боковые поверхности которых могут занимать относительно плоскостей проекций непроецирующее положение (это наклонные призмы и цилиндры), а также геометрические тела, поверхности которых непроецирующие — это конус, сфера, торы, глобоид, эллипсоид, параболоид и гиперболоиды. Сюда же относятся наклонный эллиптический цилиндр, имеющий круговые сечения, и наклонный круговой конус.
предмета, на которой следует начинать решение задачи, и границы введения посредников.
Для построения проекций точек, принадлежащих линии пересечения поверхностей, способом посредников следует применять общий для всех рассматриваемых способов графический алгоритм.
Графический алгоритм I:
1-е действие. Ввести вспомогательную плоскость или поверхность-посредник.
2-е действие. Построить вспомогательные линии пересечения плоскости — или поверхности-посредника с каждой из заданных поверхностей.
3-е действие. Определить точки пересечения построенных вспомогательных линий пересечения — эти точки принадлежат искомой линии пересечения.
Рассмотрим на примерах применение различных способов вспомогательных посредников для построения проекций линий пересечения поверхностей.
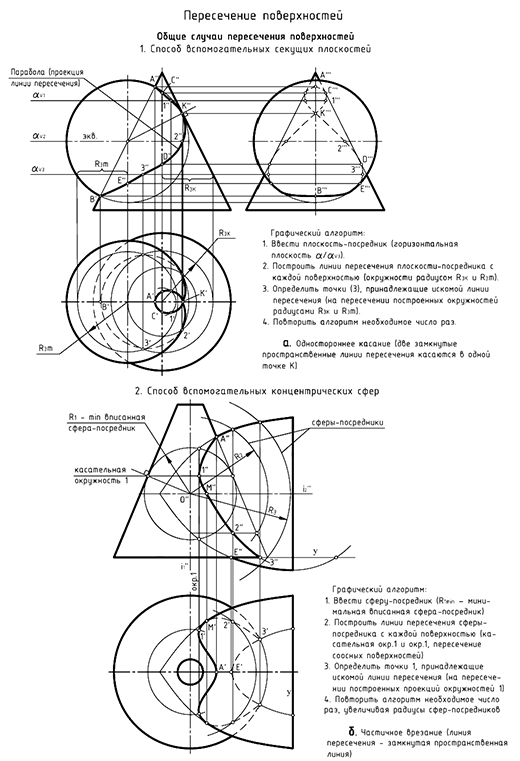
Способ вспомогательных секущих плоскостей уровня
Применение способа вспомогательных секущих плоскостей рационально при наличии д в у х графических условий:
- Общая плоскость симметрии пересекающихся геометрических тел является плоскостью уровня; при соблюдении этого условия точки пересечения
очерков поверхностей принадлежат искомой линии пересечения и определяют верхнюю и нижнюю границу введения плоскостей-посредников на соответствующей проекции предмета.
- Сечениями геометрических тел в одной из плоскостей уровня должны быть простые в построении линии пересечения — прямые линии (образующие) или окружности; эту плоскость уровня и следует выбрать в качестве посредника.
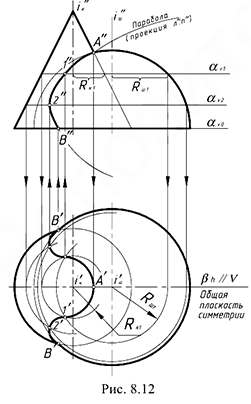
На рис. 8.12 показан пример построения проекций линии пересечения прямого конуса и половины шара.
Для решения задачи требуется предварительно выполнить графический анализ заданных проекций предмета:
А. Выбираем для решения задачи способ вспомогательных секущих плоскостей, так как здесь соблюдены два Рис. 8.12 графических условия его применения:
- общая плоскость симметрии
геометрических тел — конуса и полушара — является фронтальной плоскостью уровня (первое условие применения);
- горизонтальные плоскости уровня, которые пересекают поверхности конуса и полушара по окружностям, выбираем в качестве вспомогательных плоскостей-посредников (второе условие применения).
Б. Решение задачи, то есть введение плоскостей-посредников, начинаем на фронтальной проекции предмета, так как общая плоскость симметрии геометрических тел является фронтальной плоскостью уровня.
В. Определяем границы введения плоскостей-посредников — это точка 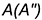
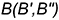
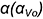
Построить проекции точек искомой линии пересечения, выполнив действия предложенного графического алгоритма I:
1-е действие. Ввести на фронтальной проекции предмета первую вспомогательную секущую горизонтальную плоскость-посредник 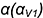
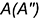
2-е действие. Построить на горизонтальной проекции предмета вспомогательные окружности радиусами 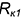
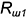
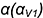
3-е действие. Определить на пересечении построенных вспомогательных окружностей горизонтальные проекции точек 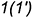
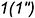
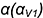
3.1. Повторить действия основного графического алгоритма, введя вторую плоскость-посредник 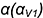
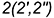
4-е действие. Соединить проекции построенных точек на фронтальной и горизонтальной проекциях предмета плавными кривыми линиями с учетом их видимости на проекциях: на фронтальную проекцию предмета пространственная кривая пересечения проецируется в видимую плоскую кривую второго порядка (участок параболы), поскольку горизонтальная проекция предмета имеет фронтальную симметрию; на горизонтальную проекцию предмета — в участок видимой кривой 4-го порядка сложной формы.
5-е действие. Оформить очерки поверхностей на заданных проекциях предмета с учетом их относительной видимости:
- на фронтальной проекции — очерк конуса существует влево от точки
, а очерк шара вправо от точки
(несуществующие очерки конуса и шара оставить тонкими линиями);
- на горизонтальной проекции — окружность основания конуса существует влево от точек
, а окружность основания шара существует
вправо от точек 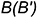
. Способ вспомогательных секущих плоскостей позволяет строить одновременно две проекции искомой линии пересечения.
Способ вспомогательных концентрических сфер
Основанием для применения сферы в качестве вспомогательной поверх-ности-посредника являются две ее характерные особенности:
- в сфере можно провести через ее центр бесконечное количество осей;
- сфера может быть соосна любой поверхности вращения; соосные поверхности пересекаются по окружностям, проекции которых легко построить (см. рис. 8.7 и 8.8).
Сфера-посредник образует две пары соосных поверхностей с каждой из заданных поверхностей. Каждая образованная пара соосных поверхностей пересекается по соответствующим окружностям, которые проецируются в прямые, перпендикулярные общей оси каждой пары, и проходят через точки пересечения очерков каждой пары соосных поверхностей.
Применение способа вспомогательных концентрических сфер для построения линии пересечения поверхностей возможно при наличии трех следующих графических условий:
- Пересекаются поверхности вращения (кроме открытого и закрытого тора).
- Общая плоскость симметрии пересекающихся поверхностей является плоскостью уровня; при этом условии точки пересечения очерков на проекции предмета, изображенного на параллельной общей плоскости симметрии плоскости проекций, принадлежат искомой линии пересечения.
- Оси поверхностей пересекаются; точка пересечения осей является центром всех вспомогательных сфер.
На рис. 8.13 показан пример построения проекций линии пересечения усеченного конуса и тороида (самопересекающийся тор).
Рассмотренный способ вспомогательных секущих плоскостей здесь применять не следует, так как ни одна плоскость уровня не пересекает поверхности одновременно по окружностям (одно из условия применения).
Для решения задачи требуется предварительно выполнить графический анализ заданных проекций предмета.
А. Выбираем для решения задачи способ вспомогательных концентрических сфер, так как здесь соблюдены три графических условия его применения:
- пересекаются поверхности вращения — прямой круговой конус и тороид (самопересекающийся тор);
- общая плоскость симметрии геометрических тел
является фронтальной плоскостью уровня;
- оси поверхностей пересекаются в точке
— центр всех вспомогательных сфер.
Б. Решение задачи, то есть введение вспомогательных сфер-посредников начинаем на фронтальной проекции предмета, так как общая плоскость симметрии является фронтальной плоскостью уровня и точки 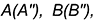
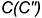
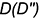
В. Определяем границы введения сфер — это точки 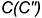
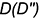
Построить проекции точек линии пересечения, выполнив действия предложенного графического алгоритма I.
1-е действие. Ввести на фронтальной проекции вспомогательную сферу-посредник минимального радиуса 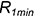
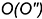
2-е действие. Построить проекции вспомогательных окружностей пересечения двух пар соосных поверхностей, образованных сферой-посред-ником с каждой заданной поверхностью:
- первая пара соосных поверхностей — сфера-посредник и тороид -имеют горизонтальную общую ось
и пересекаются по окружности касания
, которая проецируется в прямую линию (совпадает с осью конуса);
- вторая пара соосных поверхностей — сфера-посредник и конус имеют вертикальную общую ось вращения
и пересекаются по двум вспомогательным окружностям
, которые проецируются в прямые линии;
3-е действие. Определить точки 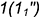
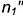
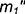
. Здесь имеет место случай полного проницания (II случай), и линия пересечения распадается на две замкнутые кривые.
Дополнительные действия:
4-е действие. Повторить действия основного графического алгоритма, введя вспомогательные сферы большего радиуса 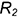
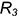
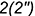
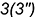
4.1. Достроить горизонтальные проекции построенных точек линии пересечения по принадлежности параллелям конуса.
4.2. Соединить проекции построенных точек на фронтальной и горизонтальной проекциях предмета плавными кривыми линиями с учетом их видимости на проекциях (только линия пересечения 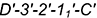
5-е действие. Оформить очерки поверхностей на заданных проекциях предмета с учетом их относительной видимости.
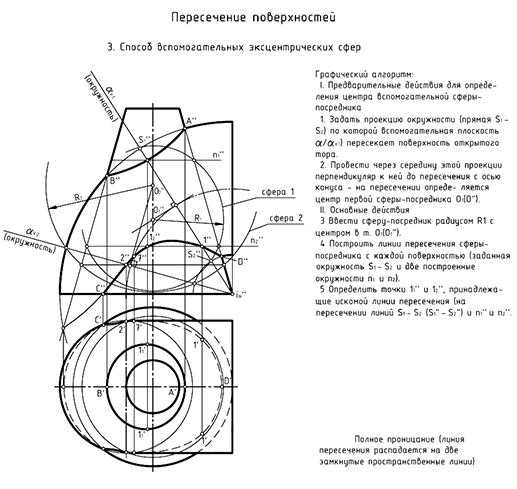
Способ вспомогательных эксцентрических сфер
Наименование способа говорит о том, что вспомогательные сферы имеют разные центры, которые и нужно определять в процессе построения проекций линии пересечения поверхностей.
Способ вспомогательных эксцентрических сфер для построения линии пересечения поверхностей возможно применять при наличии трех следующих графических условий:
- Пресекаются:
- поверхности вращения 4-го порядка, т. е. торовые поверхности — открытый или закрытый тор;
- поверхности эллиптических цилиндра и конуса, имеющие круговые сечения.
- Общая плоскость симметрии поверхностей является плоскостью уровня.
- Оси поверхностей пересекаются или скрещиваются.
Поскольку в этом способе центр каждой вспомогательной сферы нужно определять графическими построениями, первое действие графического алгоритма для построения проекций точек линии пересечения дополняется построением центра каждой вспомогательной сферы.
Порядок графических действий для построения линий пересечения способом вспомогательных эксцентрических сфер показан на двух примерах.
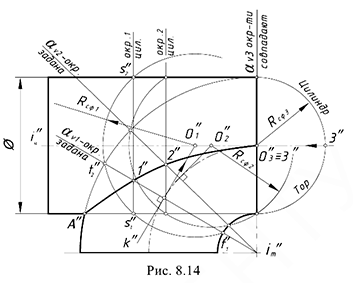
На рис. 8.14 показан пример построения проекции линии пересечения профильно-проецирующего цилиндра с поверхностью четвертой части открытого тора. Задача решается способом вспомогательных эксцентрических сфер, так как здесь соблюдены три необходимых условия для применения этого способа:
- одна из пересекающихся поверхностей — открытый тор, имеющий круговые сечения во фронтально-проецирующих плоскостях, проходящих через его ось вращения
- общая плоскость симметрии поверхностей — фронтальная плоскость уровня (подразумевается), поэтому точка
пересечения фронтальных очерков принадлежит искомой линии пересечения;
- оси поверхностей
и
скрещиваются.
Построение проекций точек линии пересечения поверхностей выполняется на заданной фронтальной проекции предмета по предлагаемому графическому алгоритму II.
Графический алгоритм II.
1-е действие. Ввести вспомогательную сферу, выполнив предварительно следующие графические действия.
1.1. Задать произвольное круговое сечение поверхности тора фронтально-проецирующей плоскостью 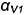
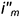
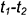
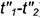
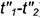
1.2. Провести к прямой 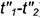
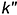
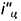
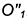
1.3. Провести окружность — проекцию вспомогательной сферы-посредника — с центром в точке 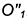
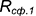
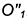
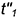
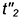
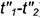
2-е действие. Построить проекцию окружности пересечения построенной сферы-посредника с поверхностью соосного ей цилиндра — это прямая 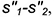
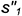
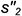
3-е действие. Определить на пересечении построенных проекций заданной окружности 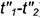
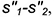
Дополнительные действия:
4-е действие. Повторить действия графического алгоритма и построить достаточное количество точек линии пересечения. В данном примере дополнительными сечениями вспомогательных плоскостей 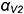
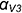
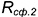
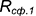
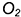
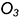
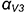
5-е действие. Соединить на фронтальной проекции точки 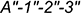
6-е действие. Оформить очерки поверхностей на заданной проекции.
На рис. 8.15 показан пример построения линии пересечения наклонного кругового цилиндра 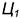
Выполнить графический анализ условия и исключить нерациональный способ решения задачи.
Рассмотренный способ вспомогательных секущих плоскостей применять не следует, так как на заданной фронтальной проекции ни одна плоскость уровня не пересекает поверхности одновременно по окружностям или образующим (одно из условий применения).
Рассмотренный способ вспомогательных концентрических сфер применять нельзя, так как проведенные сферы с центром в точке пересечения осей образуют соосные пары только с одной заданной поверхностью 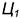
Выбираем для решения задачи способ вспомогательных эксцентрических сфер, так как здесь соблюдены три условия его применения:
- пересекаются наклонный круговой цилиндр
и эллиптический цилиндр
(поверхность не вращения);
- общая плоскость симметрии поверхностей является фронтальной плоскостью уровня (подразумевается);
- оси поверхностей
и
— пересекаются.
Решение задачи, то есть введение сечений цилиндра 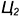
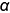
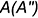
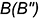
Определяем границы введения сечений цилиндра 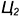
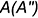
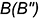
Построить проекции точек линии пересечения поверхностей, выполнив действия предложенного графического алгоритма II.
Графический алгоритм II.
1-е действие. Ввести вспомогательную сферу, выполнив предварительные графические действия.
1.1. Задать произвольное круговое сечение эллиптического цилиндра 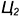
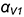
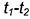
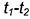
1.2. Провести к прямой 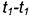
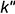
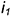
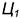
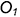
1.3. Провести окружность сферы-посредника радиусом 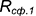
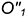
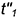
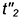
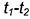
2-е действие. Построить проекцию окружности пересечения сферы-посредника с соосной ей поверхностью кругового цилиндра 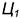
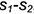
3-е действие. Определить на пересечении заданной окружности 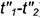
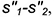
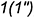
4-е действие. Повторить действия графического алгоритма II и построить проекции точек 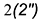
5-е действие. Соединить на фронтальной проекции точки 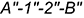
6-е действие. Оформить очерки поверхностей на заданной проекции.
Структуризация материала восьмой лекции в рассмотренном объеме схематически представлена на рис. 8.16 (лист 1). На последующих листах 2-5 приведены иллюстрации к этой схеме для быстрого визуального закрепления изученного материала при повторении (рис. 8.17-8.20).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://studizba.com/lectures/47-matematika/651-analiticheskaya-geometriya/12337-221-proekciya-linii-peresecheniya-dvuh-poverhnostey-na-koordinatnuyu-ploskost.html
http://lfirmal.com/peresechenie-poverhnostej-i-sposobyi-postroeniya-linij-presecheniya/

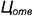 в шаре, соосных относительно профильно-проецирующей оси
в шаре, соосных относительно профильно-проецирующей оси 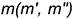 , соединяющей эти точки соприкосновения (точки касания).
, соединяющей эти точки соприкосновения (точки касания).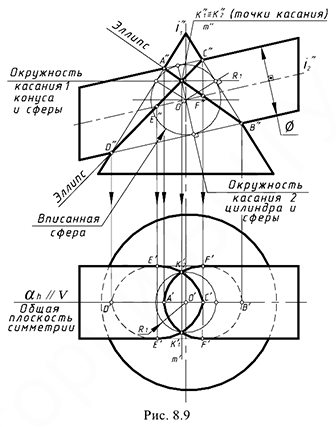
 .
.
 геометрических тел — конуса и полушара — является фронтальной плоскостью уровня (первое условие применения);
геометрических тел — конуса и полушара — является фронтальной плоскостью уровня (первое условие применения);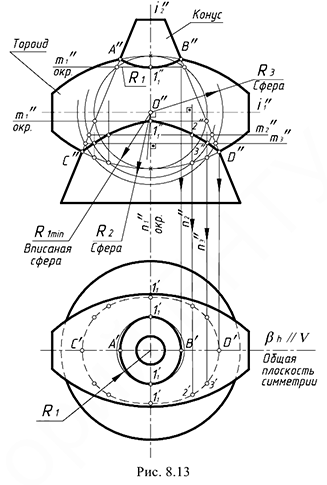
 и пересекаются по окружности касания
и пересекаются по окружности касания  и пересекаются по двум вспомогательным окружностям
и пересекаются по двум вспомогательным окружностям 
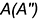 пересечения фронтальных очерков принадлежит искомой линии пересечения;
пересечения фронтальных очерков принадлежит искомой линии пересечения;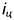 и
и 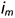 скрещиваются.
скрещиваются.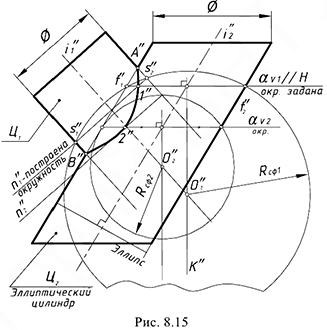
 и
и  — пересекаются.
— пересекаются.