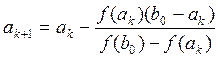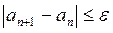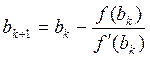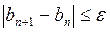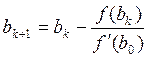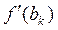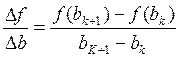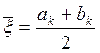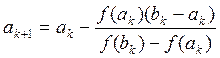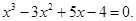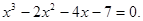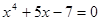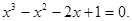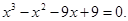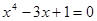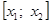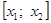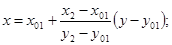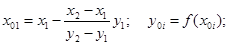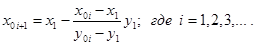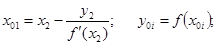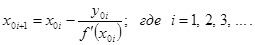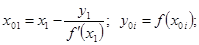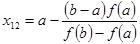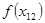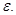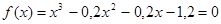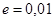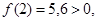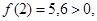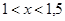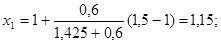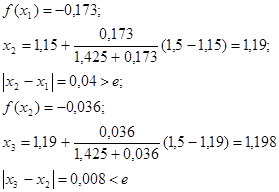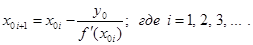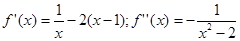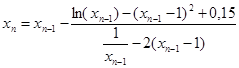Вычисление комбинированным методом действительного корня заданного уравнения
Страницы работы
Содержание работы
Министерство образования и науки Украины
Национальный аэрокосмический университет им.Н.Е.Жуковского
Отчёт по лабораторной работе №3
Решение алгебраических и трансцендентных уравнений комбинированным методом
Цель: вычислить комбинированным методом с точностью до 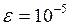
1. Графически найти интервал изоляции корня для заданного уравнения
2. Нахождение корня уравнения методом хорд:
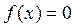
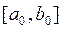
Неподвижной является точка, в которой знак функции и второй производной совпадает.
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
3. Нахождение корня уравнения методом Ньютона (метод касательных):
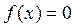
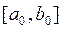
Неподвижной является точка, в которой знак функции и второй производной совпадает.
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
4. Нахождение корня уравнения модифицированным методом Ньютона:
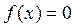
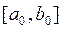
Неподвижной является точка, в которой знак функции и второй производной совпадает.
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
5. Нахождение корня уравнения методом секущих:
Если итерации 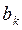
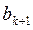
в алгоритме Ньютона можно заменить её приближённым значением в виде отношения:
Для использования этого метода необходимо знать два начальных приближения 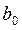
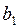
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
6. Нахождение корня уравнения комбинированным методом:
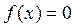
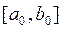
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методами хорд и касательных.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Решение алгебраических и трансцендентных уравнений методами хорд и касательных.
— применить умения отделять корни алгебраических уравнений;
— применить умения решать алгебраические уравнений приближенными методами (метод хорд и касательных);
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
1. Методом хорд с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.
2. Методом касательных с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.
3. Комбинированным методом хорд и касательных решить уравнение с точностью до 0,01.
1. Методом хорд с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.
2. Методом касательных с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.
3. Комбинированным методом хорд и касательных решить уравнение с точностью до 0,01.
1. Внимательно прочитать тему и цель практической работы .
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Предположим, что удалось найти достаточно малый промежуток 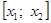
Тогда, согласно теореме 5, непрерывная и дифференцируемая функция 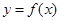
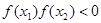
Предположим, также, что промежуток 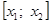
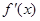
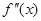
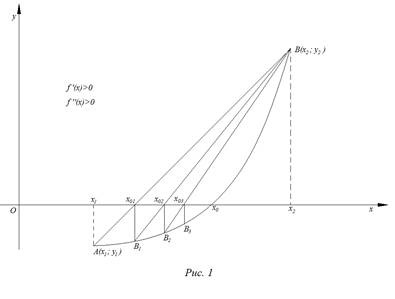
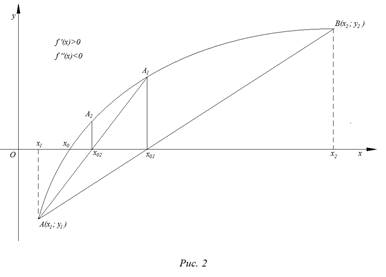
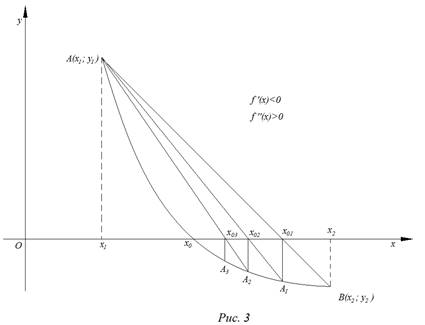
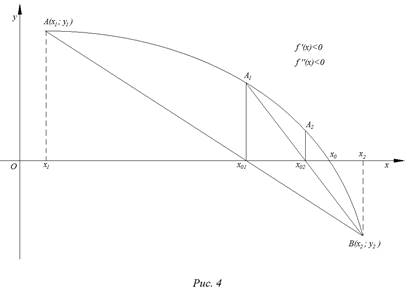
На рис. 1 – 4 изобразим схематические графики четырёх типов расположения дуги кривой.
Отдельно рассмотрим и опишем два случая.
Случай 1. 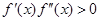
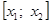
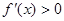
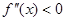
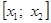
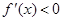
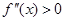
Случай 2. 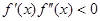
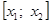
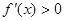
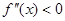
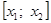
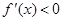
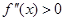
Приведем алгоритм решения задачи в первом случае:
а) через точки 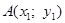
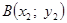
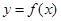
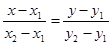
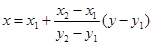
б) найдём абсциссу точки пересечения хорды АВ с осью Ох. Положив 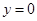
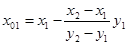
в) подставив значение 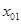
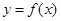
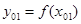
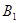
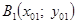
г) через точки 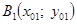
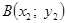
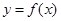
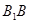
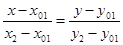
д) найдем абсциссу точки пересечения хорды 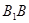
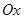
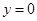
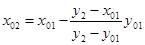
е) в результате получим последовательность значений 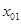
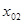
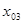
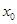
После выполнения неравенства 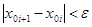
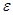
Итак, в первом случае вычисления производятся по формулам:
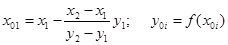
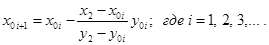
Приведем алгоритм решения задачи во втором случае:
а) значения 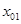
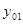
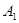
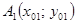
б) через точки 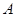
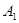
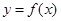
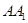
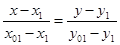
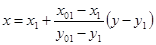
в) найдем абсциссу точки пересечения хорды 
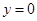
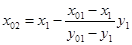
г) дальнейшие действия такие же, как и в первом случае. Итак, во втором случае вычисления производятся по формулам:
Метод касательных (метод Ньютона).
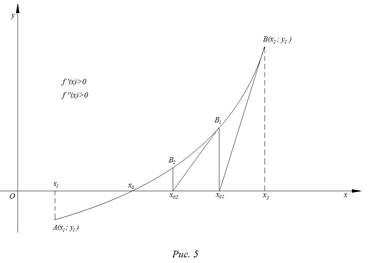
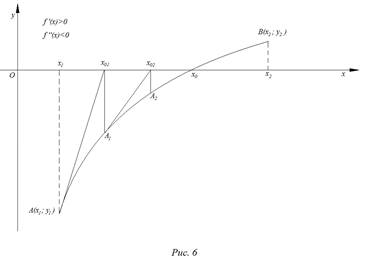
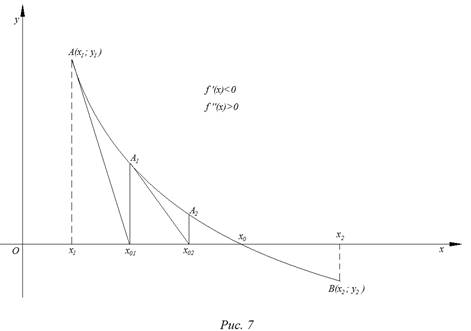
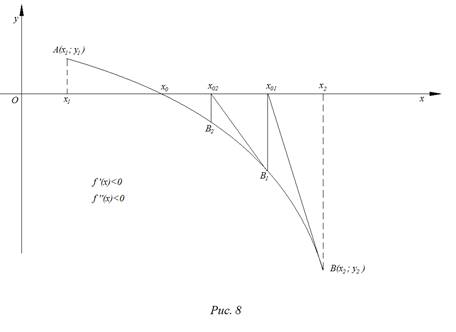
При тех же предложениях, что и в методе хорд на рис. 5 и 8, изобразим схематически графики четырех типов расположения дуги кривой.
Отдельно рассмотрим и опишем два случая.
Случай 1. . 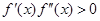
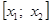
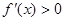
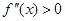
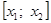
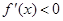
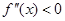
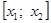
Случай 2. 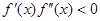
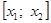
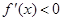
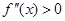
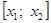
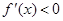
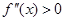
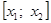
Приведем алгоритм решения задачи в первом случае:
а) через точку 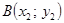
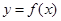
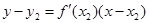
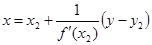
б) найдём абсциссу точки пересечения этой касательной с осью Ox . Положив 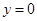
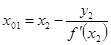
в) подставив значение 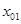
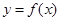
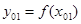
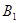
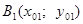
г) через точку 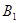
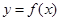
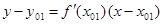
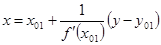
д) найдём абсциссу точки пересечения этой касательной с осью Ox . Положив 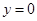
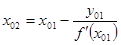
е) в результате получим последовательность значений 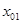
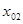
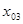
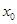
После выполнения неравенства 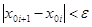
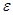
Итак, в первом случае вычисления производятся по формулам:
Алгоритм решения задачи во втором случае будет таким же, как и в первом случае, только первая касательная будет проводиться через точку 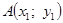
Итак, во втором случае вычисления проводятся по формулам:
Комбинированный метод хорд и касательных.
Пусть требуется найти действительный корень уравнения 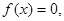
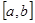
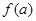
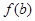
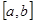
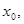
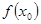
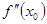
Воспользуемся формулами методов хорд и касательных:
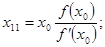
Величины 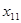
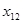
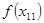
Построим новую пару приближений к корню:
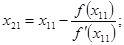
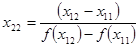
Точки 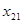
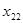
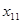
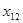
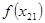
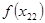
Вычислим теперь значения
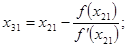
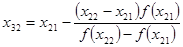
Каждая из последовательностей
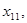
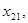
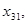
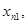
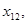
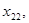
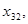
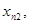
стремится к искомому корню, причем одна из последовательностей монотонно возрастает, а другая – монотонно убывает. Пусть, например, 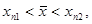
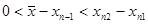
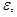
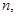
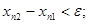
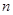
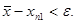
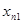
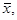
Так, например, для нахождения приближенного значения 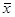
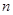
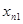
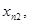
При выполнении практической работы рассмотрите следующие примеры:
Методом хорд найти положительный корень уравнения
С точностью
Прежде всего, отделяем корень. Так как
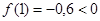
То искомый корень х лежит в интервале 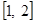
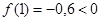
То искомый корень х лежит в интервале 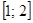
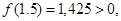
Так как 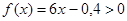
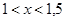
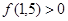
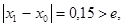
Таким образом, можно принять 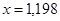
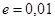
Заметим, что точный корень уравнения 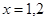
С помощью графического метода отделить корни трансцендентного уравнения и уточнить их методом Ньютона с точностью е=0,00001.
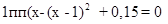
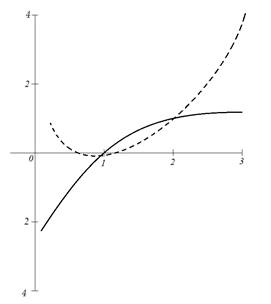
Решение. Запишем наше уравнение в виде 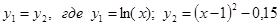
Из рис. 3 видно, что данное уравнение имеет два корня: первый корень принадлежит отрезку [0,1; 1], а второй [1,1; 2].
Итерационная формула метода Ньютона в данном случае принимает вид.
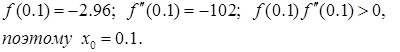
http://znanio.ru/media/metodicheskie-ukazaniya-po-vypolneniyu-prakticheskoj-raboty-po-chislennym-metodam-tema-reshenie-algebraicheskih-i-transtsendentnyh-uravnenij-metodami-hord-i-kasatelnyh-2568013