Найти все решения кватернионных уравнений

Решение квадратных уравнений над телом кватернионов

В данной презентации рассмотрены основные операции в теле кватернионов, а также способы решения некоторых видов квадратных уравнений

Просмотр содержимого документа
«Решение квадратных уравнений над телом кватернионов»

Тригонометрическая форма кватерниона

Пусть дан кватернион

Представление кватерниона q в виде:

называется его тригонометрической формой.

Так как и то можно считать мнимой единицей. Причем, у каждого кватерниона своя мнимая единица. В этом заключается существенное отличие тригонометрической формы кватерниона от тригонометрической формы комплексного числа.

Возведение кватерниона в степень

Пусть кватернион q записан в тригонометрической форме:

Тогда справедлива формула

Аналогичная формула имеет место и для возведения в степень комплексного числа.

Извлечение корня n- ой степени из кватерниона

Пусть кватернион q записан в тригонометрической форме:

И пусть Тогда справедлива формула

Аналогичная формула имеет место и для извлечения корня n- ой степени из комплексного числа.

Корень квадратный из кватерниона a имеет бесконечно много значений, находящихся по формуле:

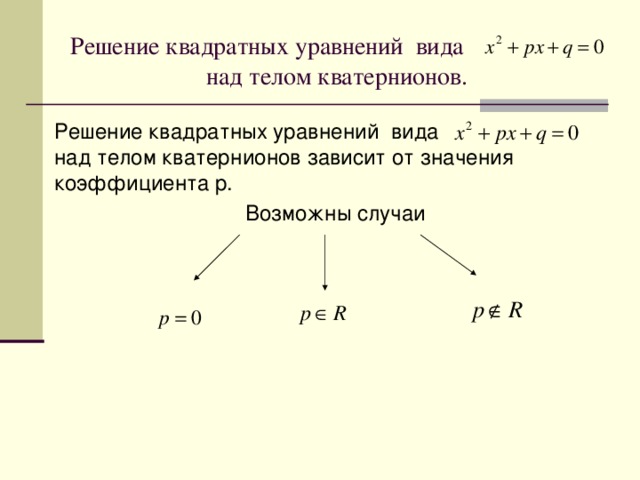
Решение квадратных уравнений вида над телом кватернионов.

Решение квадратных уравнений вида над телом кватернионов зависит от значения коэффициента p .

Значение находится по формуле извлечения корня n- ой степени из кватерниона. Уравнение имеет два различных решения

, два различных решения

, бесконечно много решений

Решение уравнения находится по следующей формуле.

Причем, если то уравнение может иметь одно, два или бесконечно много решений.

Если то уравнение имеет два различных решения.

Ищем решение уравнения в виде

Тогда возможны две ситуации

Введем мнимую единицу

Уравнение будет иметь два различных решения, которые находятся по формуле:

Пусть выполняется условие

При этом условии

Тогда уравнение имеет два различных решения, которые находятся по следующей формуле:

Алгебра кватернионов

Примером тела, не являющегося полем, может служить алгебра кватернионов («четырехмерных чисел»).

Сначала напомним, как строится алгебра комплексных чисел. Комплексное число определяется как упорядоченная пара действительных чисел, причем сложение пар вводится покомпонентно:

Заметим, что покомпонентное определение умножения не дало бы требуемых свойств этой операции (таких же, как у умножения действительных чисел), поскольку при покомпонентном умножении имеются делители нуля:

При стандартном определении умножения согласно (2.3) можно доказать, что алгебра комплексных чисел является полем.

Кватернионы определяются как упорядоченные пары комплексных чисел. Сложение кватернионов вводится снова как покомпонентное, а умножение — следующим образом:

где — число, комплексно сопряженное с .

Можно показать, что каждый кватернион однозначно представляется в виде

где — действительные числа, а и — кватернионы, называемые мнимыми единицами. Правила умножения мнимых единиц вместе с обычной единицей задаются табл. 2.3.

Можно заметить, что умножение попарно различных мнимых единиц совершается по тем же правилам, что и векторное умножение ортов в векторной алгебре.

Сопряженный с кватернион, по определению, равен . Имеют место следующие тождества:

Действительное число , обозначаемое , называется нормой кватерниона .

Свойства кватернионов

Построенная таким образом алгебра кватернионов обладает следующими свойствами:

1. Умножение кватернионов ассоциативно, но не коммутативно. Это свойство непосредственно выводится из табл. 2.3. Например, пусть

2. В алгебре кватернионов нет делителей нуля. Действительно, тогда и только тогда, когда , т.е. нулевому кватерниону , и можно показать, что . Тогда, если , то

Таким образом, по умножению все ненулевые кватернионы образуют группу и алгебра кватернионов оказывается телом, не будучи полем.

Алгебра и числа Кэли

Из кватернионов можно также строить упорядоченные пары, вводя операции сложения и умножения как описано выше, а операцию сопряжения согласно формуле ( и — кватернионы). Полученная таким образом алгебра называется алгеброй Кэли , а ее элементы — числами Кэли или октавами. Умножение в алгебре Кэли уже не будет даже ассоциативным, однако ассоциативный закон имеет место в частном случае — для любых двух чисел Кэли и

Кроме того, каждое ненулевое число Кэли имеет обратное. Другими словами, в алгебре Кэли любое уравнение (или ) имеет единственное решение. Таким образом, алгебра Кэли также является алгеброй без делителей нуля. Можно доказать, что, кроме алгебры комплексных чисел, алгебры кватернионов и алгебры Кэли, не существует «многомерных» числовых алгебр без делителей нуля.