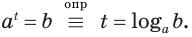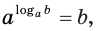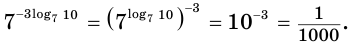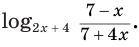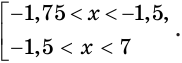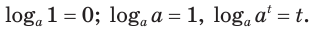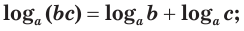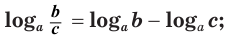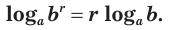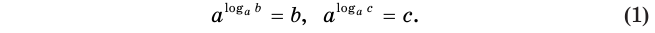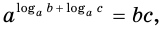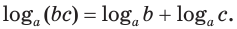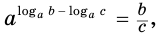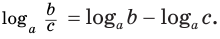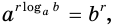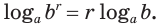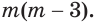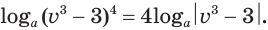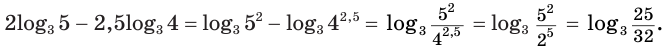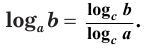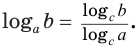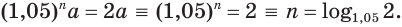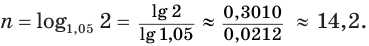Решение логарифмических уравнений
Данный калькулятор позволяет найти решение логарифмических уравнений.
Логарифмическое уравнение – это уравнения, в которых переменная величина находится под знаком логарифма. Логарифмическая функция всегда монотонна и может принимать любые значения. Кроме того, переменный аргумент логарифма должен быть больше нуля и переменное основание логарифма должно быть положительным и не равным единице.
При решении логарифмических уравнений зачастую необходимо логарифмировать или потенцировать обе части уравнения. Логарифмировать алгебраическое выражение — выразить его логарифм через логарифмы отдельных чисел, входящих в это выражение. Потенцирование – нахождение выражения, от которого получен результат логарифмирования.
Для того чтобы найти корни логарифмического уравнения, нужно ввести это уравнение в ячейку и нажать на кнопку «Вычислить». В ответе отображаются корни уравнения и график логарифмической функции.
Калькулятор поможет найти решение логарифмических уравнений онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
| Основные функции |
: x^a
Логарифмические выражения с примерами решения
Мы уже умеем по значению
Пример:
Решим уравнение 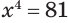
По определению арифметического корня находим, что 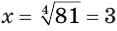
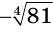
Теперь поставим задачу нахождения показателя 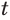
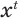
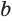
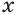
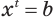
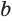
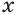
Пример:
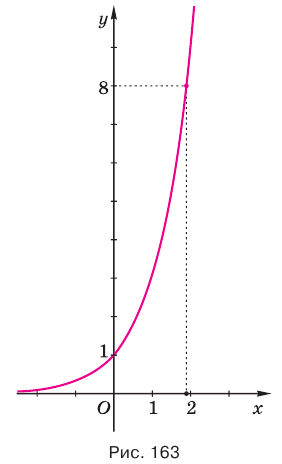
Решим уравнение 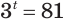
Это уравнение можно записать как 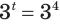
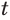
Обратим внимание на то, что при решении уравнения 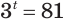
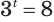
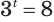
Этот корень называют логарифмом числа 8 по основанию 3 и обозначают 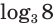
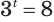
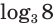
Логарифмом числа 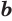
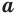
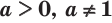
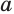
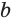
Логарифм числа 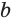
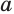
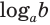
Пример:
Таким образом, учитывая определение логарифма числа, корень уравнения 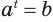
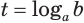
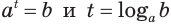
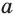
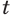
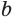
Пример:
Решим уравнение 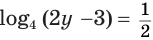
Определение логарифма позволяет данное уравнение заменить равносильным уравнением 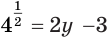
Определение логарифма коротко можно представить равенством
которое называют основным логарифмическим тождеством.
Пример:
Вычислим значение выражения 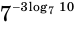
Используем свойство возведения степени в степень и основное логарифмическое тождество:
Из свойств показательной функции следует, что выражение 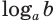
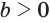
Пример:
Найдем область определения выражения
Данное выражение имеет значение, если основание логарифма 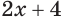
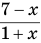
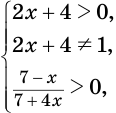
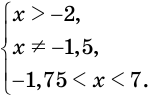
Из определения логарифма следует, что
Действие нахождения логарифма числа называется логарифмированием.
Введение действия логарифмирования порождает новый класс логарифмических выражений, т. е. выражений, которые содержат по крайней мере одно действие нахождения логарифма из выражения с переменной. При преобразованиях логарифмических выражений используются свойства действия логарифмирования. Установим эти свойства.
Теорема 5.
При любом положительном и не равном единице основании:
логарифм произведения положительных множителей равен сумме их логарифмов:
логарифм частного с положительными делимым и делителем равен разности логарифмов делимого и делителя:
логарифм любой действительной степени положительного числа равен произведению показателя степени и логарифма основания:
Доказательство:
Пусть 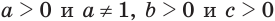
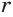
Основное логарифмическое тождество позволяет записать равенства:
Перемножив их, получим:
откуда, по определению логарифма:
Если разделить первое равенство из (1) на второе, то получим, что
откуда, по определению логарифма:
Возведя первое равенство из (1) в степень с показателем 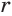
откуда, по определению логарифма:
Обращаем внимание на то, что при применениях тождеств, установленных теоремой 5, нужно следить за тем, чтобы все подлогарифмические выражения были положительными.
Пример:
а) 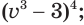
а) Получим
б) Выражение 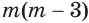
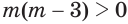
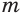
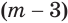
Если оба множителя 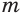
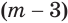
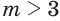
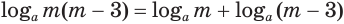
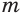
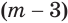
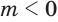
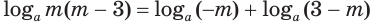
Действие, обратное логарифмированию, называют потенцированием.
Пример:
Пропотенцируем выражение 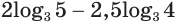
Будем последовательно получать:
Логарифмы чисел находят с помощью специальных таблиц или калькулятора. И в том, и в другом случае находят десятичные или натуральные логарифмы.
Десятичным логарифмом числа называют логарифм этого числа по основанию 10.
Для десятичного логарифма вместо 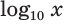
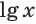
Натуральным логарифмом числа называют логарифм этого числа по основанию 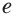
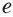
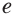
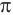
Для натурального логарифма вместо 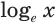
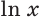
Для вычислений достаточно иметь возможность находить логарифмы по одному основанию, так как тогда можно найти логарифм числа по другому основанию. Это позволяет делать формула перехода к другому основанию.
Теорема 6.
Логарифм числа по данному основанию равен логарифму числа по новому основанию, деленному на логарифм данного основания по новому основанию:
Доказательство:
Пусть 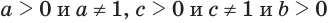
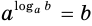
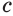
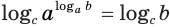
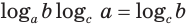
Пример:
Найдем, через сколько лет удвоится пятипроцентный вклад в банк.
Пусть имеется вклад в 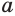
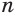
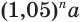
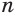
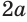
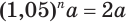
Вычисления проведем с помощью калькулятора, на котором есть клавиша для нахождения десятичных логарифмов:
Таким образом, удвоение пятипроцентного вклада произойдет через 14,2 года.
Открытие логарифмов было вызвано в XVI в. быстрым развитием астрономии и усложнением астрономических вычислений, которые имели непосредственное практическое значение при определении местонахождения судов по Солнцу и другим звездам. Логарифмы быстро вошли в практику.
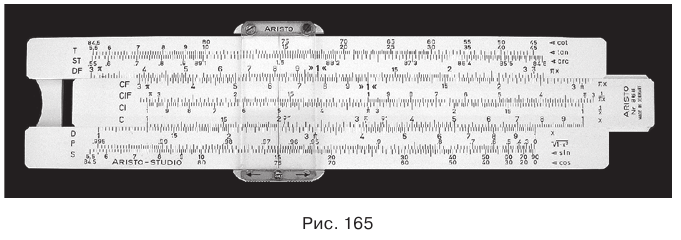
Первые логарифмические таблицы были составлены в одно время и независимо друг от друга шотландским математиком Джоном Непером (1550—1617) и швейцарским математиком и астрономом Йобстом Бюрги (1552—1632). В 1623 г. английский математик Эдмунд Гантер изобрел логарифмическую линейку, с помощью которой действия над числами — умножение, деление — заменяются действиями сложения и вычитания над логарифмами этих чисел. На рисунке 165 показана одна из логарифмических линеек. Сейчас нужные вычисления проводятся с помощью калькуляторов. Леонард Эйлер (1707—1783) установил, что действие логарифмирования является обратным действию возведения в степень. Термин логарифм предложен Джоном Непером. Современное определение логарифма впервые дано в 1742 г. английским математиком Вильямом Гардинером.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Показательная функция, её график и свойства
- Производные показательной и логарифмической функций
- Показательно-степенные уравнения и неравенства
- Показательные уравнения и неравенства
- Дифференцируемые функции
- Техника дифференцирования
- Дифференциальная геометрия
- Логарифмическая функция, её свойства и график
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Логарифмическое уравнение: решение на примерах
Как решить логарифмическое уравнение? Этим вопросом задаются многие школьники, особенно в преддверии сдачи ЕГЭ по математике. Ведь в задании С1 профильного ЕГЭ могут встретиться именно логарифмические уравнения.
Уравнение, в котором неизвестное находится внутри логарифмов, называется логарифмическим. Причем неизвестное может находится как в аргументе логарифма, так и в его основании.
Способов решения таких уравнений существует несколько. В этой статье мы разберем способ, который легко понять и запомнить.
Как решать уравнения с логарифмами: 2 способа с примерами
Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:

При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!
Давайте посмотрим, как это работает на примере:
Воспользуемся определением логарифма и получим:
Теперь перед нами простейшее уравнение, решить которое не составит труда:
Сделаем проверку. Подставим найденный Х в исходное уравнение:
Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.
Поэтому мы покажем еще один способ решения логарифмических уравнений.
Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:
Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.
Решим еще раз то же самое уравнение, но теперь этим способом:
Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:


Воспользуемся этим свойством в нашем случае, получим:

Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.
Разберем другой пример:



Теперь делаем проверку:
Еще один пример решения логарифмического уравнения:






Теперь подставим х2 = -5 в исходное уравнение:
Пример решения логарифмического уравнения с разными основаниями
Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,

Итак, разберем наш пример:
Мы знаем, что 1/3 = 3 -1 . Еще мы знаем свойство логарифма, а именно вынесение показателя степени из логарифма:

Тогда получим:



Пример решения логарифмического уравнения с переменными основаниями
Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т.е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, logx+1(х 2 +5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.



1. Аргумент логарифма должен быть больше ноля, следовательно:
2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:
Сведем все требования в систему:
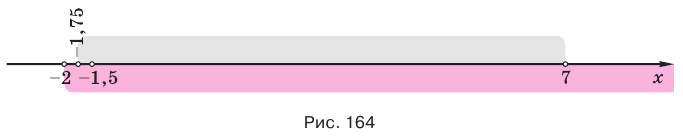
Данную систему требований мы можем упростить. Смотрите х 2 +5х-5 больше ноля, при этом оно приравнивается к (х + 1) 2 , которую в свою очередь так же больше ноля. Следовательно, требование х 2 +5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:




Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:
Т.к. 3 2 =9, то последнее выражение верно.
Как сделать проверку
Еще раз обращаем ваше внимание, что при решении логарифмических уравнений необходимо учитывать область допустимых значений. Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т.е. больше ноля.
Если наше уравнение имеет вид loga (f(x)) = loga (g(x)), то должны выполняться следующие ограничения:
После решения логарифмического уравнения нужно обязательно сделать проверку. Для этого вам необходимо подставить получившееся значения в исходное уравнение и посчитать его. Времени это займет немного, зато позволит не записать в ответ посторонние корни. Ведь так обидно правильно решить уравнение и при этом неправильно записать ответ!
Итак, теперь вы знаете, как решить логарифмическое уравнение с помощью определения логарифма и с помощью преобразования уравнения, когда в обеих его частях стоят логарифмы с одинаковыми основаниями, которые мы можем «зачеркнуть». Отличное знание свойств логарифма, учет области определения, выполнение проверки – залог успеха при решении логарифмических уравнений.
http://www.evkova.org/logarifmicheskie-vyirazheniya
http://yourrepetitor.ru/kak-reshit-logarifmicheskoe-uravnenie/

 : x^a
: x^a