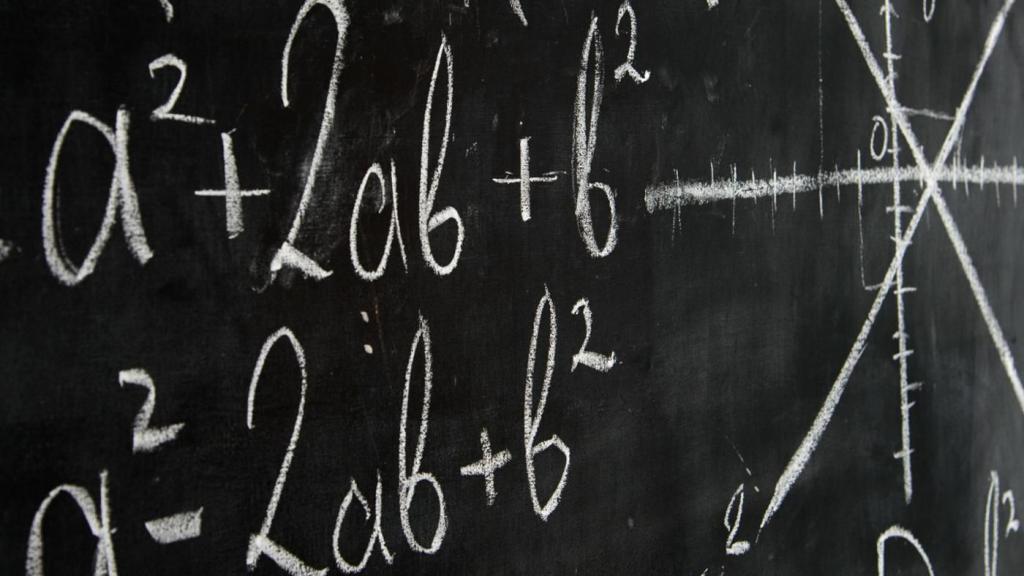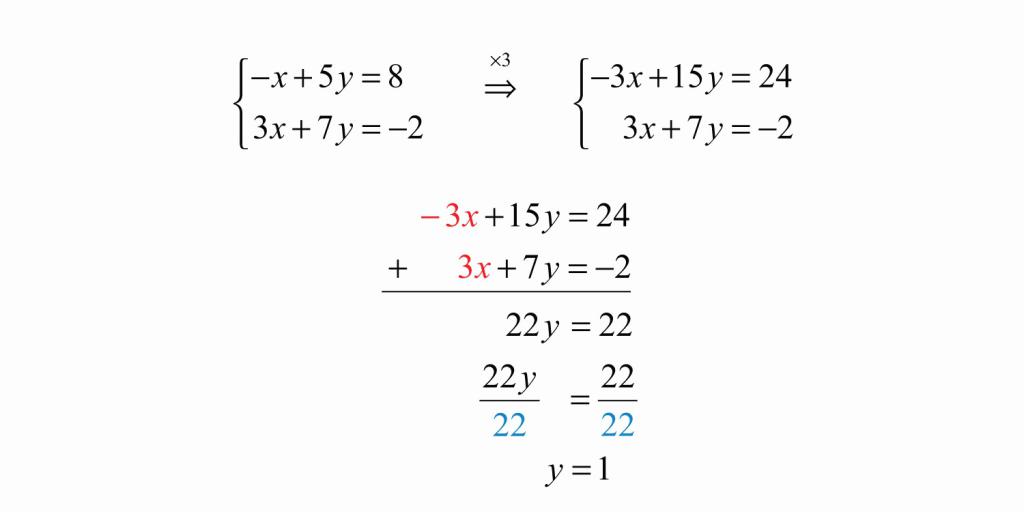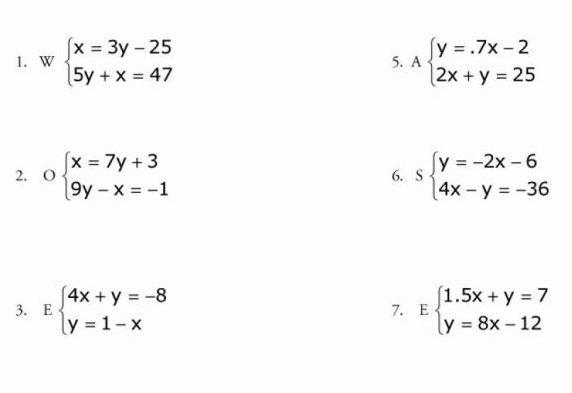Название переменных в уравнении функции

Что такое переменные? Переменная величина в математике

Значение переменных в математике велико, ведь за время ее существования ученые успели совершить множество открытий в данной области, и, чтобы кратко и ясно изложить ту или иную теорему, мы пользуемся переменными для записи соответствующих формул. Например, теорема Пифагора о прямоугольном треугольнике: a 2 = b 2 + c 2 . Чем каждый раз при решении задачи писать: по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов — мы записываем это формулой, и все сразу становится понятно.

Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.

Понятие переменной

Для начала узнаем, что такое переменная? Это численная величина, которая может принимать множество значений. Она не может быть постоянной, так как в разных задачах и уравнениях для удобства решения мы принимаем за переменную разные числа, то есть, например, z — это общее обозначение для каждой из величин, за которые ее принимают. Обычно их обозначают буквами латинского или греческого алфавита (x, y, a, b и так далее).

Есть разные виды переменных. Ими задаются как некоторые физические величины — путь (S), время (t), так и просто неизвестные значения в уравнениях, функциях и других выражениях.

Например, есть формула: S = Vt. Здесь переменными обозначаются определенные величины, имеющие отношение к реальному миру — путь, скорость и время.

А есть уравнение вида: 3x — 16 = 12x. Здесь уже за x принимается абстрактное число, которое имеет смысл в данной записи.

Виды величин

Под величиной имеется в виду то, что выражает свойства определенного предмета, вещества или явления. К примеру, температура воздуха, масса животного, процентное содержание витаминов в таблетке — это все величины, числовые значения которых можно вычислить.

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).

Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.

Возьмем прямолинейное равномерное движение. Точка в пространстве движется с одинаковой скоростью на каждом промежутке времени. То есть изменяются время и расстояние, а скорость остается одинаковой. В данном примере время и расстояние — переменные величины, а скорость — постоянная.

Или, например, “пи”. Это иррациональное число, которое продолжается без повторяющейся последовательности цифр и не может быть записано полностью, поэтому в математике оно выражается общепринятым символом, который принимает только значение данной бесконечной дроби. То есть “пи” — это постоянная величина.

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.

С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:

x 4 + 15x 2 + 7 = 0

За x 2 принимаем некое k, и уравнение приобретает понятный вид:

x 2 = k, при k ≥ 0

Вот какую пользу в математику несет введение переменных.

Неравенства, примеры решения

Неравенство представляет собой запись, в которой два математических выражения или два числа связаны знаками сравнения: , ≤, ≥. Они бывают строгими и обозначаются знаками или нестрогими со знаками ≤, ≥.

Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

1. При переносе числа из одной части неравенства в другую меняем его знак на противоположный.
2. При умножении или делении частей неравенства на отрицательное число их знаки меняются на противоположные.
3. Если умножить или разделить обе части неравенства на положительное число, то получится неравенство, равное исходному.

Решить неравенство — значит найти все допустимые значения переменной.

Пример с одной переменной:

Решаем, как обычное линейное уравнение — переносим слагаемые с переменной влево, без переменной — вправо и приводим подобные члены:

Делим обе части неравенства на 10 и получаем:

Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.

Квадратные неравенства

Если взять квадратное уравнение вида ax 2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

y = ax 2 + bx + c — это квадратичная функция. Ее мы можем решить с помощью дискриминанта, либо используя теорему Виета. Вспомним, как решаются подобные уравнения:

1) y = x 2 + 12x + 11 — функция является параболой. Ее ветви направлены вверх, так как знак коэффициента «a» положительный.

2) x 2 + 12x + 11 = 0 — приравниваем к нулю и решаем с помощью дискриминанта.

a = 1, b = 12, c = 11

D = b 2 — 4ac= 144 — 44 = 100 > 0, 2 корня

Или можно было решить это уравнение по теореме Виета:

Методом подбора получаем такие же корни уравнения.

Парабола

Итак, первый способ решения квадратного неравенства — это парабола. Алгоритм ее решения таков:

1. Определяем, куда направлены ветви параболы.

2. Приравниваем функцию к нулю и находим корни уравнения.

3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.

Решим неравенство x 2 + x — 12 > 0

Выписываем в виде функции:

1) y = x 2 + x — 12 — парабола, ветви вверх.

Приравниваем к нулю.

Дальше решаем как квадратное уравнение и находим нули функции:

3) Изображаем числовую прямую и на ней точки 3 и -4. Парабола пройдет через них, ветвями вверх и ответом к неравенству будет множество положительных значений, то есть (-∞; -4), (3; +∞).

Метод интервалов

Второй способ — это метод интервалов. Алгоритм его решения:

1. Находим корни уравнения, при которых неравенство равно нулю.

2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.

3. Определяем знак любого интервала.

4. Расставляем знаки у остальных интервалов, меняя их через один.

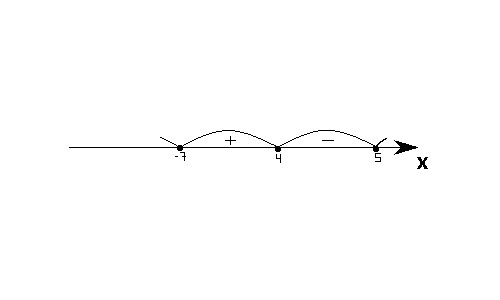
Решим неравенство (x — 4)(x — 5)(x + 7) ≤ 0

1) Нули неравенства: 4, 5 и -7.

2) Изображаем их на числовой прямой.

3) Определяем знаки интервалов.

Решим еще одно неравенство: x 2 (3x — 6)(x + 2)(x — 1) > 0

1. Нули неравенства: 0, 2, -2 и 1.

2. Отмечаем их на числовой прямой.

3. Определяем знаки интервалов.

Прямая делится на промежутки — от -2 до 0, от 0 до 1, от 1 до 2.

Возьмем значение на первом промежутке — (-1). Подставляем в неравенство. При данном значении неравенство становится положительным, значит и знак на этом промежутке будет +.

Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.

Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.

Системы уравнений

Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.

Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.

Мы изучим решение систем уравнений с двумя переменными. Есть два способа их решения — метод подстановки или алгебраический метод.

Алгебраический метод

Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.

Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:

-x + 5y = 8 , при y = 1

Решаем получившееся уравнение и находим икс.

Главное в решении системы — правильно записать ответ. Многие школьники делают ошибку и пишут:

Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:

Метод подстановки

Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.

В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:

Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:

Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

Понятие линейной функции

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

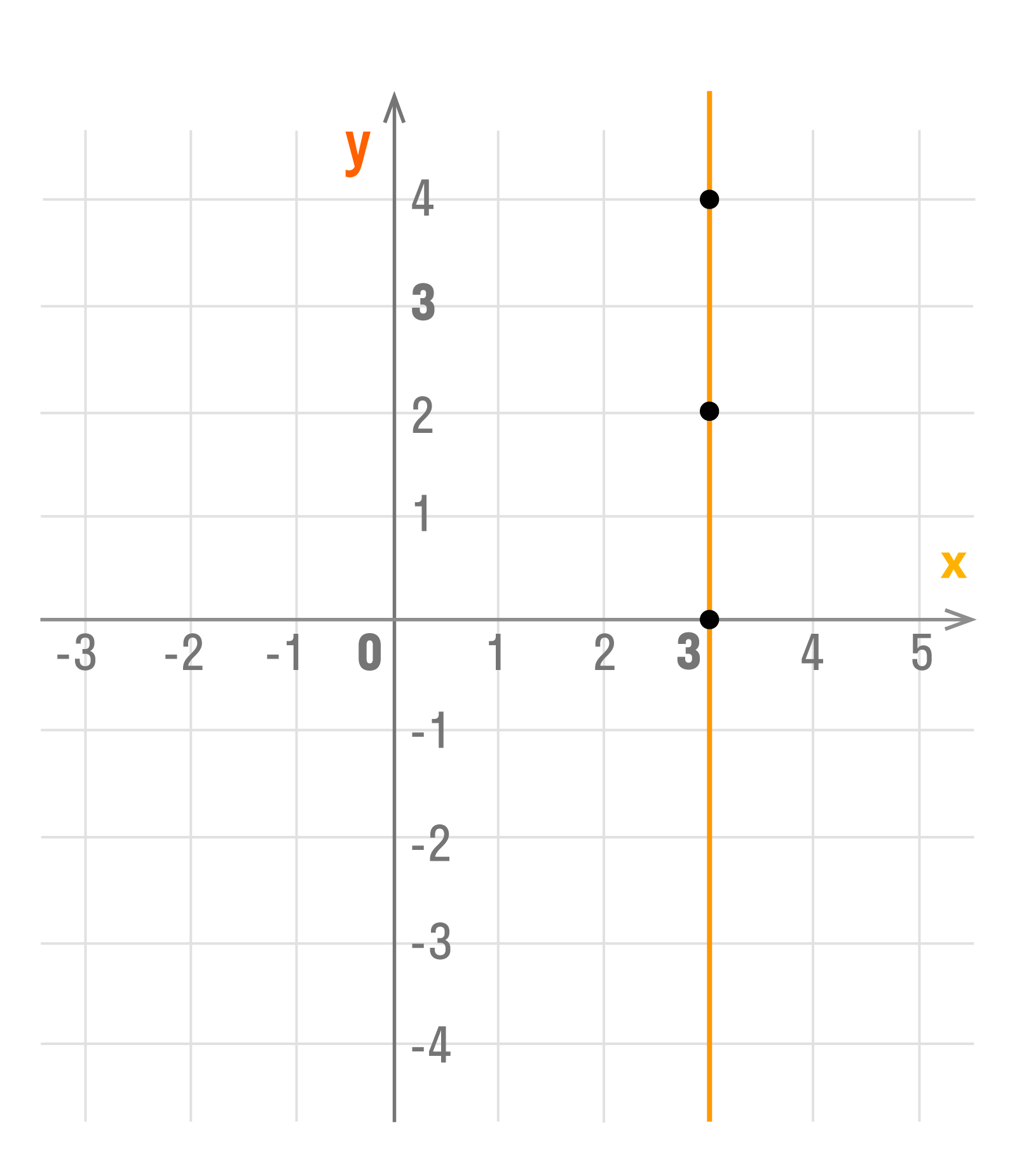
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

Функции многих переменных примеры с решением

Содержание:

Основные понятия о функциях многих переменных

Изучение связей и закономерностей, существующих в материальном мире, часто приводят к функции не одной, а многих переменных. Эти функции позволяют выражать более сложные зависимости, чем функции одной переменной. Поэтому теория функций многих переменных имеет широкое практическое применение в различных отраслях.

Определение функции многих переменных. Функция двух переменных и ее графическое изображение

Переменные x₁, x₂, . x_n называются независимыми между собой, если каждая из них может принимать произвольные значения в своей области изменения независимо от того, какие значения принимают при этом другие переменные.

Определение 1. Функцией многих переменных u = f (x₁, x₂, . x_n) называется такая закономерность, при которой переменным x₁, x₂, . x_n из некоторого множества D ⊂ R n ставится в соответствие одно значение u из множества E ⊂ R’.

Например:

Множество D называется областью определения функции u = f (x₁, x₂, . x_n), а множество E — областью значений этой функции. Например, функция задана для всех x и y, для которых выполняется неравенство x 2 + y 2 ≤ 9. В данном случае областью определения функции является круг на плоскости Оxy с центром в точке O (0; 0) и радиусом R = 3. Область значений этой функции E = [0; 3].

Частным случаем функции многих переменных есть функция двух переменных z = f (x, y), для которой можно дать понятие графика функции. В общем случае графиком такой функции является поверхность в трехмерном пространстве R 3 .

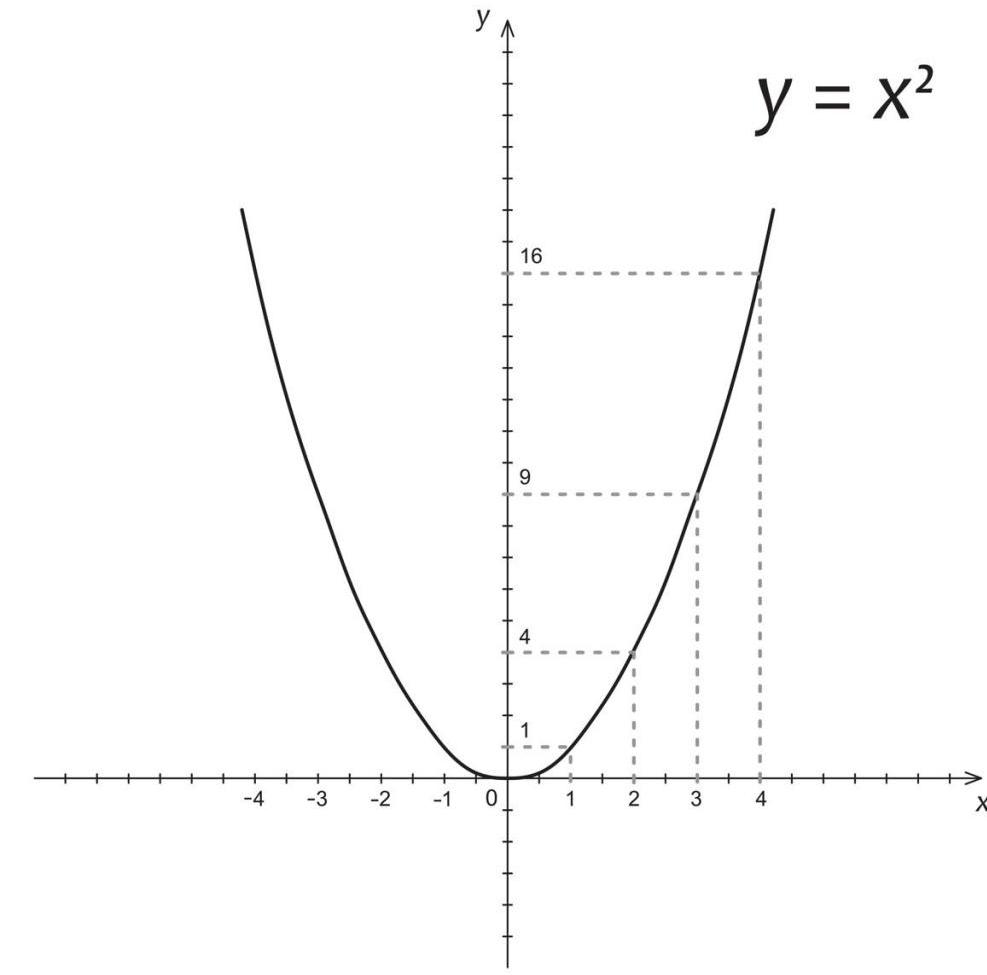
Пример 1. z = x 2 + y 2 . Графиком этой функции является параболоид вращения (рис. 1).

Экономические задачи, приводящие к понятию функций многих переменных

Приведем примеры конкретных функций многих переменных, которые встречаются в экономических задачах.

Пример 2. Пусть предприятие выпускает только один товар, и на его выпуск затрачивается только одно сырье (один ресурс). Предприятие характеризуется полностью своей производственной функцией y = f (x) — зависимость объема выпущенного товара y от объема затраченного сырья x. Такая производственная функция называется одноресурсной.

Если на производство продукции определенного типа расходуются многие виды сырья (ресурсов) x₁, x₂, . x_n , то такая производственная функция называется многоресурсной или многофакторной:
y= F (x) = F (x₁, x₂, . x_n).

Наиболее известной производственной функцией является функция Кобба-Дугласа y = AK α L β , где A, α, β — неотрицательные константы, причем α + β ≤ 1;
K — объем фондов в стоимостном или натуральном выражении;
L — объем трудовых ресурсов — число работников, число человеко-дней;
y — выпуск продукции в стоимостном или натуральном выражении.

На этом примере видно, что функция Кобба-Дугласа является функцией двух независимых переменных K и L.

Пример 3. Рассмотрим основное уравнение классической количественной теории денег, которое называется уравнением обмена Фишера: MV = PY.
В данном уравнении любая из переменных M, V, P, Y может рассматриваться как функция трех переменных, где
M — это общее количество денег, имеющихся в обороте;
V — скорость их оборота (сколько раз каждый рубль участвует в расчетах в среднем за год);
Y — национальный продукт или доход (национальный продукт — это все готовые товары и услуги, произведенные в экономической системе в стоимостном выражении; национальный доход — это все выплаты, полученные домашними хозяйствами: заработная плата, рента, прибыль; национальный продукт и национальный доход численно равны);
P — уровень цен (среднее взвешенное значение цен готовых товаров и услуг, которые определены относительно базового показателя, принятого за единицу).
Пусть , то есть цена является функцией трех независимых переменных. Тогда с увеличением денежной массы (количества денег) M в несколько раз (то есть деньги просто напечатают), цены вырастут во столько же раз, при условии, что другие величины V и Y останутся неизменными. Такие действия и является чаще всего причиной инфляции.

Функции многих переменных. Понятие функции многих переменных

Ранее рассматривались числовые функции одной переменной . Областью определения такой функции являлось множество . Числовая функция переменных характеризуется тем, что областью ее определения является подмножество пространства . В этом случае значение аргумента представляет собой точку .

Определение 1. Пусть имеются два множества и , и указано правило , по которому каждому элементу ставится в соответствие единственный элемент . Тогда говорят, что задана функция переменных из в :

. (1)

Как и ранее, — область определения функции , — область значений функции .

Для функций двух переменных ( = 2) вместо пишут обычно и тогда (1)принимает вид

. (2)

Функция двух переменных геометрически определяет некоторую поверхность в . Ее область определения состоит из точек расположенных на плоскости . Каждой из этих точек соответствует единственная число , которое является аппликатой точки данной поверхности. Поэтому говорят, что есть функция точки , и пишут . Эту аналогию можно распространить на случай > 2. Тогда область определения будет состоять из точек , а функция (1.19) будет записана в виде .

Поверхность — это сфера радиуса с центром в точке (0,0,0). Она не является функцией двух переменных, так как точке соответствуют два числа . Однако функцией будет, например, верхняя часть сферы (рис. 1, а).

Другим примером функции двух переменных может служить эллиптический параболоид (рис. 1, б). Если эту поверхность пересечь плоскостью, параллельной плоскости , то линией пересечения будет эллипс. Если же плоскость пересечения параллельна или , то линией пересечения будет парабола.

Уравнением задается гиперболический параболоид. График этой функции двух переменных имеет форму седла (рис. 1, в). Если эту поверхность пересечь плоскостью, параллельной плоскости , то линией пересечения будет гипербола. Если же плоскость пересечения параллельна или , то линией пересечения будет парабола.

Еще одним примером функции многих переменных может служить производственная функция Кобба-Дугласа. Ее классический вид

(3)

где — объем выпуска продукции; где — затраты труда; где — затраты производственных фондов (рис. 2). Константы и — положительны, как и переменные , , . Сумма параметров , и 1-, равна единице. Это означает, что при увеличении производственных ресурсов и на одну единицу объем продукции также увеличивается на единицу. Следовательно, темпы роста перечисленных показателей совпадают.

Исследования показали, что зависимость (3) редко встречается на практике. Поэтому справедлив более общий вид производственной функции Кобба-Дугласа:

(4)

где — положительная константа. В отличие от предыдущего случая сумма параметров может быть как больше, так и меньше единицы. Если > 1, то темпы роста объема выпуска продукции выше, чем темпы роста производственных ресурсов и . Если же

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.