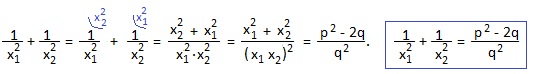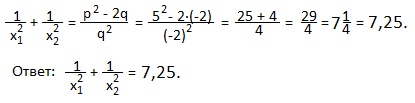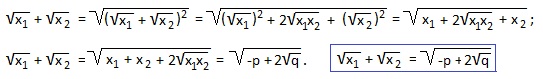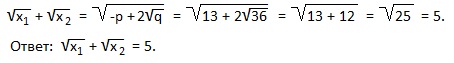По теореме Виета, не вычисляя сами корни, можно найти их сумму и
По теореме Виета, не вычисляя сами корни, можно найти их сумму и произведение. Соотношения между корнями и коэффициентами квадратного уравнения позволяют в некоторых случаях находить его корни устно, не прибегая к формуле корней.
Слайд 8 из презентации «Теорема Виета»
Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Теорема Виета.ppt» можно в zip-архиве размером 199 КБ.
Похожие презентации
«Теорема Виета 8 класс» — Умножишь ты корни, и дробь уж готова: В числителе “_________”, в знаменателе “а”. Заполнить таблицу. Алгебра 8 класс. И сумма корней тоже дроби равна. Теорема обратная Теореме Виета. Теорема Виета.
«Сумма векторов» — Правило треугольника. Правило многоугольника. АВ А – начало вектора В – конец вектора. Сумма векторов Правило треугольника Правило параллелограмма Правило многоугольника. Сумма векторов. Правило параллелограмма. Вектор – направленный отрезок. Содержание Понятие вектора. Презентация предназначена для использования на уроках повторения по теме «Векторы» в 8 классе.
«История теоремы Пифагора» — Исторический обзор начнем с древнего Китая. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. А на каждом катете построен квадрат, содержащий два треугольника. И руководствуйся подлинным знанием — лучшим возничим. Из истории теоремы Пифагора. Здесь особое внимание привлекает математическая книга Чу-пей.
«Решение квадратных уравнений теорема Виета» — Один из корней уравнения равен 5. Найдите другой корень уравнения и свободный член с. Один из корней уравнения равен -3. Руководитель: учитель математики Баранникова Е. А. Решение квадратных уравнений с применением теоремы Виета. Воспользуемся теоремой Виета: Один из корней уравнения равен 12. Работу выполнила: ученица 8 класса Слинько В.
«Урок теорема Пифагора» — Определить вид треугольника: Вычислите высоту CF трапеции ABCD. Доказательство теоремы. И обрете лестницу долготою 125стоп. Решение простейших задач. Доказательство. Определить вид четырехугольника KMNP. Показ картинок. Теорема Пифагора. План урока: Исторический экскурс. Разминка. Знакомства с теоремой.
«Теорема косинусов» — Доказательство. Пусть в треугольнике АВС АВ = с, ВС = а, СА = в. Докажем, например, что а? = b? + с? — 2bc cosA. Дополнительная информация. Теорему косинусов иногда называют обобщенной теоремой Пифагора. Теорема косинусов. Пользуемся теоремой косинусов в решение треугольников. Пользуемся теоремой косинусов в решении треугольников.
8.2.4. Применение теоремы Виета
Часто требуется найти сумму квадратов (x1 2 +x2 2 ) или сумму кубов (x1 3 +x2 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:
Помочь в этом может теорема Виета:
Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Выразим через p и q:
1) сумму квадратов корней уравнения x 2 +px+q=0;
2) сумму кубов корней уравнения x 2 +px+q=0.
Решение.
1) Выражение x1 2 +x2 2 получится, если взвести в квадрат обе части равенства x1+x2=-p;
(x1+x2) 2 =(-p) 2 ; раскрываем скобки: x1 2 +2x1x2+ x2 2 =p 2 ; выражаем искомую сумму: x1 2 +x2 2 =p 2 -2x1x2=p 2 -2q. Мы получили полезное равенство: x1 2 +x2 2 =p 2 -2q.
2) Выражение x1 3 +x2 3 представим по формуле суммы кубов в виде:
Еще одно полезное равенство: x1 3 +x2 3 =-p·(p 2 -3q).
Примеры.
3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x1 2 +x2 2 .
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения
x1+x2=-p=3, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 1) равенство:
x1 2 +x2 2 =p 2 -2q. У нас -p=x1+x2=3 → p 2 =3 2 =9; q=x1x2=-4. Тогда x1 2 +x2 2 =9-2·(-4)=9+8=17.
4) x 2 -2x-4=0. Вычислить: x1 3 +x2 3 .
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения x1+x2=-p=2, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 2) равенство: x1 3 +x2 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.
Ответ: x1 3 +x2 3 =32.
Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.
5) 2x 2 -5x-7=0. Не решая, вычислить: x1 2 +x2 2 .
Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.
По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.
Решаем так же, как пример 3), используя равенство: x1 2 +x2 2 =p 2 -2q.
x1 2 +x2 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.
Ответ: x1 2 +x2 2 =13,25.
6) x 2 -5x-2=0. Найти:
Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x1 2 +x2 2 =p 2 -2q.
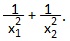
В нашем примере x1+x2=-p=5; x1∙x2=q=-2. Подставляем эти значения в полученную формулу:
7) x 2 -13x+36=0. Найти:
Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.
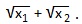
У нас x1+x2=-p=13; x1∙x2=q=36. Подставляем эти значения в выведенную формулу:
Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!
http://mathematics-repetition.com/8-2-4-primenenie-teorem-vieta/