Некоторые приемы решения целых уравнений видеоурок

Урок «Некоторые приемы решения целых уравнений»

Краткое описание документа:

Видеоурок «Некоторые приемы решения целых уравнений» помогает освоить приемы, помогающие решить более эффективно целые уравнения с различными особенностями. При помощи данного материала расширяется и углубляется понятие учеников о способах решения уравнений, формируются навыки поиска эффективных способов решения.

Задача видеоурока – при помощи подробного объяснения с использованием анимации и других приемов, применяемых для лучшей наглядности, облегчить понимание материала, представить его в наиболее удобном виде для понимания и запоминания.

Видеоурок начинается в представления темы. Ученикам напоминается, что нахождение корней многочлена высокой степени осложняется, так как удобных формул на нахождения корней нет или они вовсе не выведены. Поэтому для решения уравнений, содержащих многочлены высоких степеней, применяются методы, основанные на особенностях решаемых уравнений. В зависимости от особенностей уравнения, могут быть применены разные способы решения – к примеру, уже рассмотренный метод интервалов.

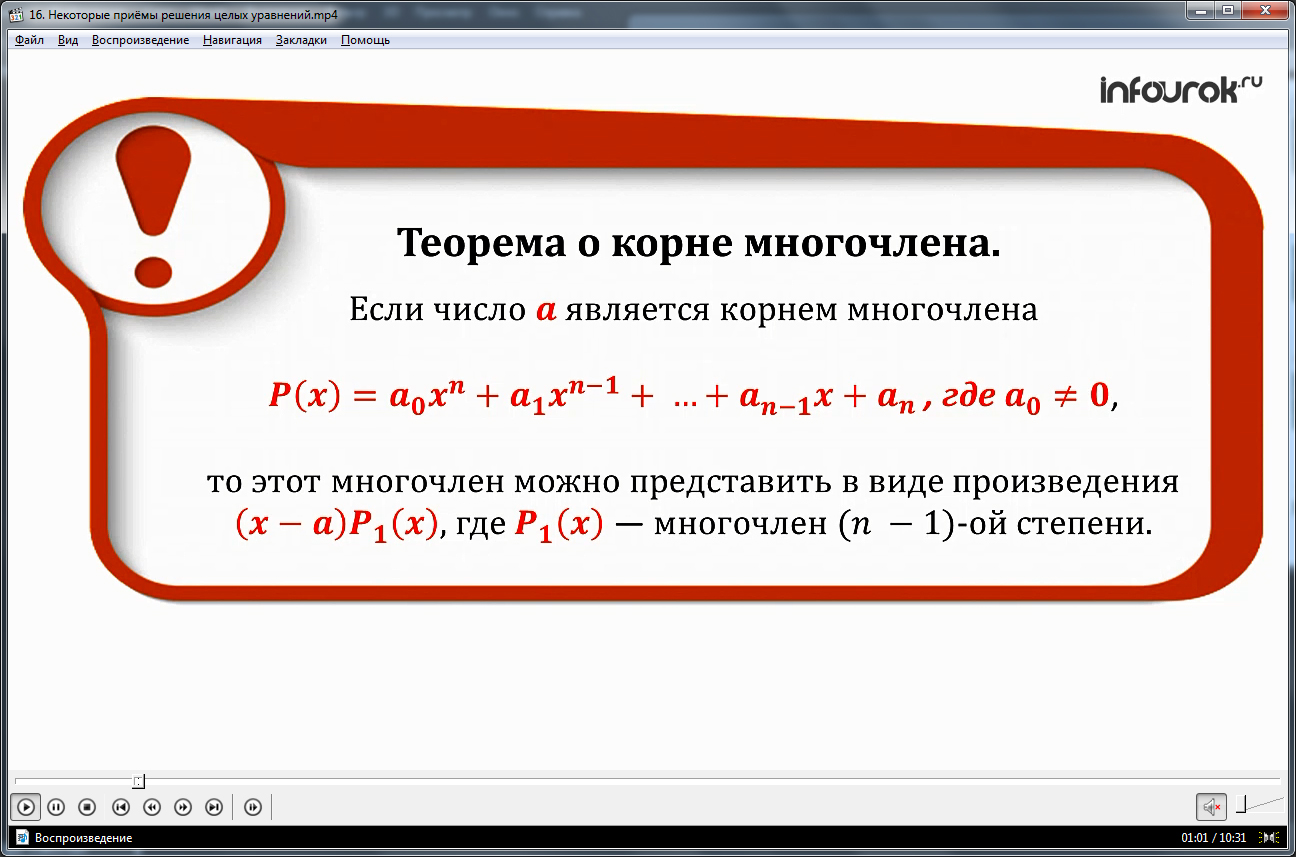
Некоторые уравнения высоких степеней решают, используя выводы теоремы о корне многочлена, которая формулируется на экране. Суть теоремы состоит в том, что при известном корне а многочлена вида P(x)=a₀x n +a₁x n-1 +…+a_n-1x+a_n, в котором a₀≠0, многочлен может быть представлен в виде произведения (х-а)Р₁(х). При этом Р₁(х) – многочлен степени (n-1). Отмечается, что для уравнения с одной переменной, целыми коэффициентами и одним корнем, поиск корня можно выполнить, используя теорему о целых корнях целого уравнения.

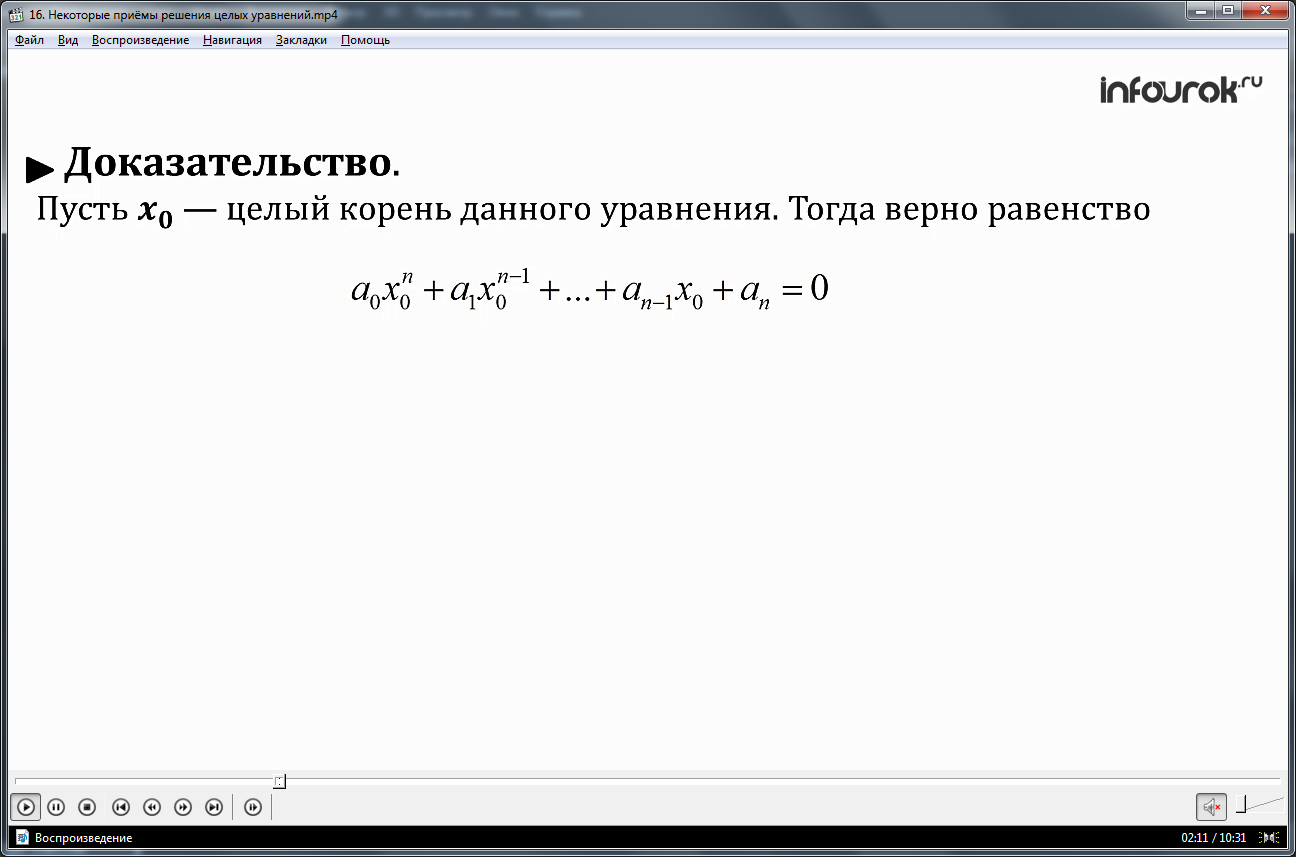
Текст теоремы о целых корнях целого уравнения выведен на экран и выделен для записи в тетради и лучшего запоминания. Он гласит о том, что если уравнение a₀x n +a₁x n-1 +…+a_n-1x+a_n=0, в котором a_n≠0, а a₀, a₁, a₂… являются целыми числами, имеет целый корень, этот корень — делитель свободного члена. Приводится доказательство данной теоремы. Чтобы доказать справедливость суждения, допускается, что х₀ – целый корень уравнения. При его подстановке в уравнение, получается a₀x₀ n +a₁x₀ n-1 +…+a_n-1x₀+a_n=0. При переносе свободного члена в правую часть уравнения, в оставшемся выражении можно вывести за скобки общий множитель х₀. Получится уравнение вида a_n= x₀(-a₀x₀ n-1 -a₁x₀ n-2 -…-a_n-1). Выражение в скобках является целым числом, так как x₀, -a₀, -a₁, -a₂… — целые числа. Следовательно, при делении a_n на x₀ в результате получается целое число, и x₀ является делителем свободного члена.

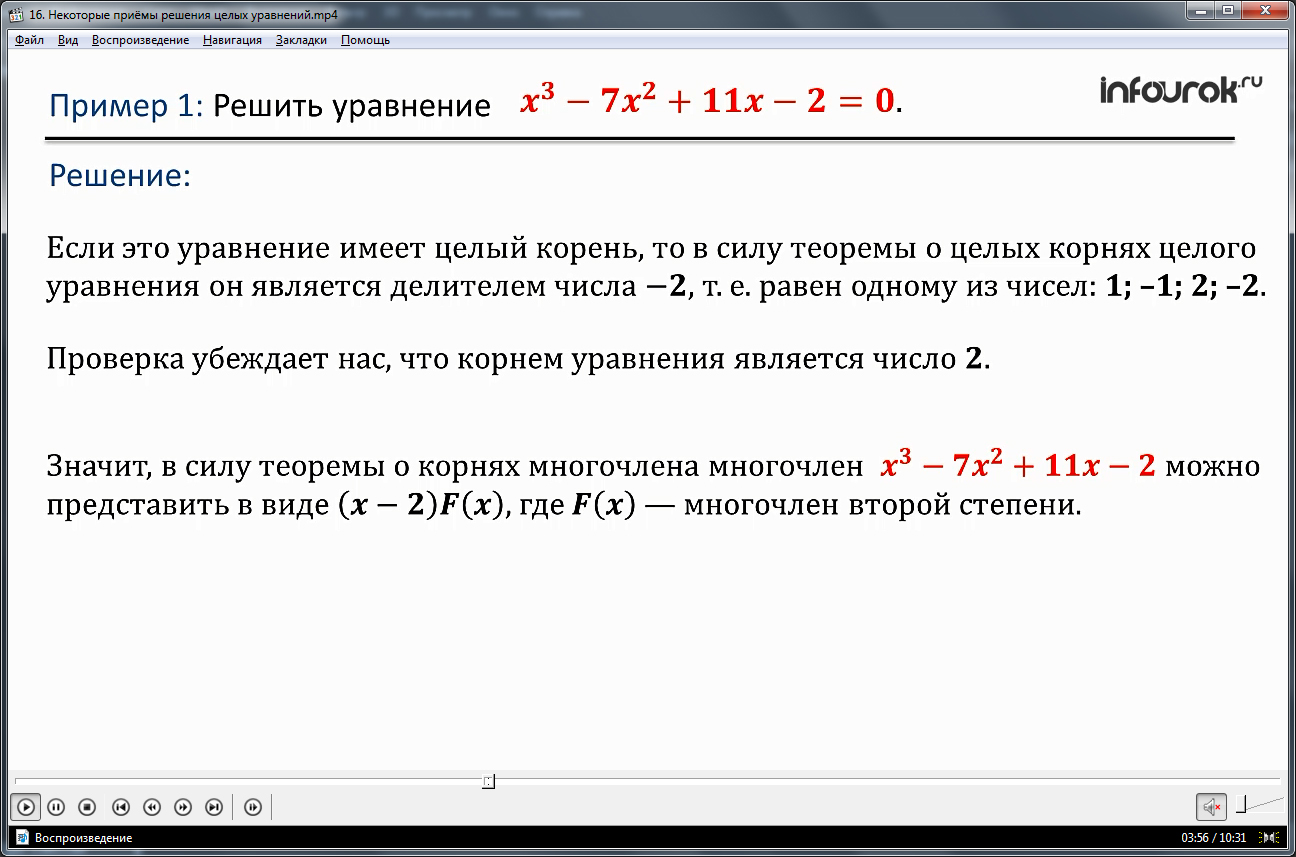
Ученикам представляется материал, помогающий научиться применять данную теорему для решения уравнений методом разложения многочлена на множители. Для этого необходимо усвоить, что уравнение Р(х)=0 решается разложением многочлена Р(х) на множители, если Р(х) – многочлен третьей и более высоких степеней. Примером подобного решения служит описанное в примере 1 решение уравнения х 3 -7х 2 +11х-2=0. Вспоминая изученную теорему о целых корнях целого уравнения, обратим внимание на свободный член уравнения. Его делителями являются числа 2, -2, 1, -1. Подставив значения корней в уравнение, можно убедиться, что корнем будет число 2. Поэтому многочлен в левой части уравнения, согласно теореме о корнях многочлена, представляем в виде (х-2)F(x), при этом F(x) является многочленом второй степени. Найти F(x) можно, выполняя деление уголком. Данный способ деления демонстрируется на экране, наглядно описывая все его особенности. В результате деления получается F(x)=х 2 -5х+1. Соответственно уравнение приобретает вид (х-2)( х 2 -5х+1)=0. Уравнение будет справедливо, если хотя бы один множитель равен нулю. То есть решение сводится к нахождению корней уравнений х-2=0 и х 2 -5х+1=0. Корень первого уравнения х₁=2 Корнями второго уравнения являются числа х₂=1/2(5+√21) и х₃=1/2(5-√21). Все три найденных значения являются корнями исходного уравнения.

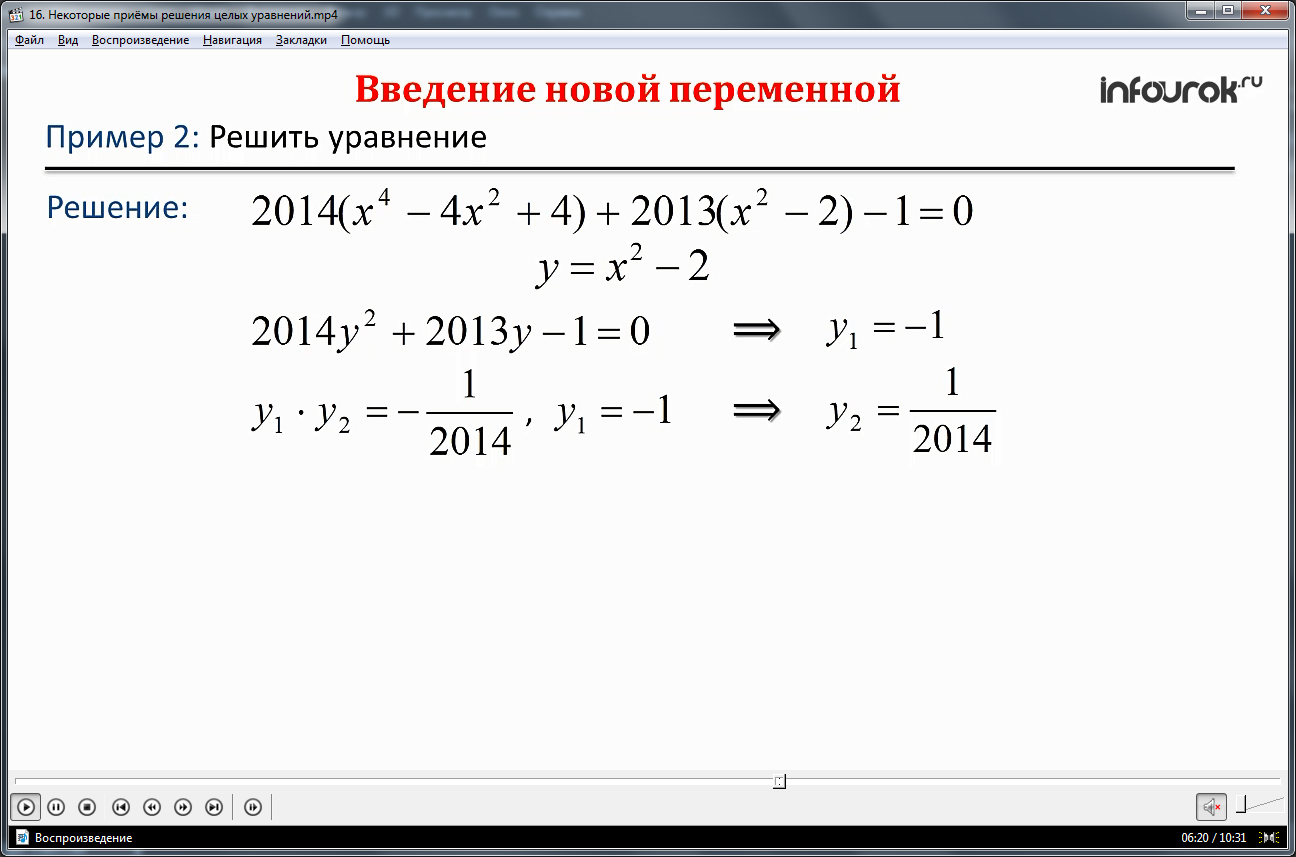
Напоминается способ введения новой переменной, который уже применялся учениками при решении биквадратных уравнений. Его использование демонстрируется в решении уравнения 2014(х 4 -4х 2 +4)+2013(х 2 -2)-1=0. Очевидно, что в выражении есть часть, которая может быть заменена переменной у, понижающей степень многочлена. После замены выражения х 2 -2 переменной у, получается квадратное уравнение 2014у 2 +2013у-1=0. Используя теорему Виета находятся корни данного уравнения – у₁=-1 и у₂=1/2014. После подстановки значений у в выражение, принятое на новую переменную, находим значения корней х. Полученные решения уравнений равны х1=1, х2=-1, х3=√4029/2014 и х4=-√4029/2014.

Отмечается, что методом введения новой переменной могут быть решены возвратные уравнения. Определение возвратных уравнений дается на экране, выделенное для запоминания. Это уравнения вида a₀x n +a₁x n-1 +…+a_n-1x+a_n=0, в которых a_k= a_n-k, k=0, 1, 2, …, n. Примером решения возвратного уравнения служит решение уравнения х 4 -7х 3 +8х 2 -7х+1=0. Отмечается, что в решении уравнения может помочь схожесть коэффициентов, которая приведет к выражению, позволяющему применить метод введения новой переменной. После деления обеих частей уравнения на х 2 , перегруппировки слагаемых и вынесения общих множителей за скобки, получаем выражение (х 2 +1/х 2 )-7(х+1/х)+8=0. За новую переменную принимается х+1/х=у. После ее подстановки получается квадратное уравнение у 2 -7у+6=0. Корнями данного уравнения являются у₁=1 и у₂=6. После подстановки значений переменной у в выражение, содержащее х, получим два уравнения для нахождения корней исходного уравнения. В результате вычисления определяются корни уравнений – х₁=3+2√2 и х₂=3-2√2.

На примере рассматривается решение уравнения, в котором используются участки возрастания и убывания функции. В уравнении х 5 +2х-3=0 согласно теореме о целом корне целого уравнения, проверяется наличие целого корня. Для этого оцениваются делители свободного члена. Проверкой выявлено, что делитель 1 является корнем данного уравнения. Для демонстрации единственности данного корня решения уравнения оценивается при помощи переброски его линейной части в правую сторону: х 5 =-2х+3. Слева в уравнении располагается возрастающая функция у= х 5 , график которой построен на рисунке. Функция, расположенная в правой части у=-2х+3 представляет собой убывающую прямую. Решение уравнения будет точкой пересечения этих двух графиков. Таким образом, можно констатировать, что решение уравнения будет одно: х=1.

Видеоурок «Некоторые приемы решения целых уравнений» помогает учителю представить информацию об особенностях решения различных уравнений, более эффективно использовать время урока. Также данный материал поможет ученику самостоятельно разобраться с решением уравнений. Также данное видео может быть полезно при дистанционном обучении.

Некоторые приемы решения целых уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Презентация по теме Учитель математики МБОУ СОШ № 13 города Костромы Коржева Наталия Александровна

Некоторые приемы решения целых уравнений Алгебра 9 класс (учебник «Алгебра» автор Ю.Н. Макарычев и др.)

Краткая аннотация. Выполнение данного проекта позволит ученику обобщить знания, полученные на уроках по решению целых уравнений и дополнить эти знания новыми теоремами, свойствами и фактами. Материал по данной теме вполне доступен для изучения учащимися 9 классов. Его изучение подготовит ребят к более успешному усвоению курса алгебры в старшей школе. Содержание материала рассчитано на сдвоенный урок.

Цели учебная: систематизация и обобщение, расширение и углубление знаний обучающихся по решению целых уравнений с одной переменной высших степеней; подготовка учащихся к применению знаний в нестандартной ситуации. развивающая: развитие личности обучающегося через самостоятельную творческую работу, развитие инициативы обучающихся; обеспечивать устойчивую мотивационную среду, интерес к изучаемой теме; развивать умение обобщать, правильно отбирать способы решения уравнения; воспитательная: развитие интереса к изучению математики, подготовка обучающихся к применению знаний в нестандартной ситуации; воспитывать волю и настойчивость для достижения конечных результатов.

Задачи обеспечивать устойчивую мотивационную среду, интерес к изучаемой теме; подготовить учащихся к применению знаний в нестандартной ситуации; развивать умение обобщать, правильно отбирать способы решения уравнений, воспитывать волю и настойчивость для достижения конечных результатов.

Оборудование Проектор Компьютер Презентация Таблицы Место проведения – кабинет информатики

Беседа с учащимися по данной теме. Мотивация изучения темы. Актуализация знаний – блиц — опрос по теме «Целые уравнения» Систематизация и обобщение знаний – сообщения обучающихся о стандартных приемах решения уравнений. Самостоятельная работа. Расширение и углубление знаний – сообщение учителя о нестандартных приемах решения уравнений. Домашнее задание: примеры на осмысление, закрепление новых знаний Структура разработки

1) х2 — 6│х│+8 = 0 2) х5 +2х+1 = 0 3) х5 +х3 +2х – 4 = 0 4) (х+1)(х+2)(х+4)(х+5) = 40 5) 2х4 +х3 -6х2 +х+2=0 6) (х+2)(х+3)(х+8)(х+12) = 4х2 7) х3 – 8х2 + 13х -2=0 8) 2х4 – 2х3 – х +1 = 0 Мотивация обучения темы

1.Какое уравнение называется целым и есть ли они среди выше представленных? 2.Как найти степень целого уравнения с одной переменной и сколько корней имеет уравнение первой, второй, третьей и т.д. степеней? 3.Могли бы вы для какого-нибудь уравнения предложить способ решения? 4. Какие способы решения уравнений вы знаете? 5. Могли бы вы предложенные способы применить для решения этих уравнений? Актуализация знаний

1. Метод разложения на множители. 2. Введение новой переменной. 3. Графический способ. Систематизация и обобщение знаний – стандартные приемы решения

Самостоятельная работа 1 вариант 2 вариант Х2– 16 =0 Х4-3х2=0 Х2+ 5х +6 +0 Х2+5х -6 +0 Х3- 8х2–х +8 =0 Х3-2х2-4х +8 =0 Х3– 3х2-4х = 0 (х – 1)2-25 = 0. (х2– 3х +1)(х2-3х +3)=3 (2х + 1)2+ 4(2х +1) = 221

Теорема о корне многочлена. Теорема целых корнях уравнения Использование свойств функций. Свойство четности функции Свойство монотонности функции Решение возвратных уравнений Расширение и углубление знаний

1) -3х7 -2х +5=0 2) (х 2 +3х)2+2 (х 2 +3х) -120=0 3) х3 +х – 4=0 4) х 2 – │10х│+21=0 5) (х+1)(х+3)(х+5)(х+7)=945 6) 27х 2 – 9х – 18=0 7) (х2 +х+6)(х2 +х-4)=144 8) х5 — х4 -2х3 +2х2 -3х +3=0 9) 2х4 +х3 — 3х2 +х +2=0. Подведение уроков

х8 – 17х4 +16=0 х3-6х2+11х-6=0 (х+1)(х+3)(х+5)(х+7) -15=0 (х+4)(х-2)(х+5)(х-10)+54х2 =0 х4 +2х3 – 6х2 +2х+1=0. х3+2х-1=0 Домашнее задание

Ю.Н. Макарычев и др., Просвещение, 2011г. У.И. Сахарчук, Л.С. Сагателова, Решение уравнений высших степеней: Волгоград, 2007. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ. Виноградов И.М. (главный редактор) Математическая энциклопедия. Б.М. Ивлев и др. Задачи повышенной трудности по алгебре и началам анализа 1990г. Литература

Основные методы решения уравнений в целых числах

Введение

Существует множество математических задач, ответами к которым служат одно или несколько целых чисел. В качестве примера можно привести четыре классические задачи, решаемые в целых числах – задача о взвешивании, задача о разбиении числа, задача о размене и задача о четырёх квадратах. Стоит отметить, что, несмотря на достаточно простую формулировку этих задач, решаются они весьма сложно, с применением аппарата математического анализа и комбинаторики. Идеи решения первых двух задач принадлежат швейцарскому математику Леонарду Эйлеру (1707–1783). Однако наиболее часто можно встретить задачи, в которых предлагается решить уравнение в целых (или в натуральных) числах. Некоторые из таких уравнений довольно легко решаются методом подбора, но при этом возникает серьёзная проблема – необходимо доказать, что все решения данного уравнения исчерпываются подобранными (то есть решений, отличных от подобранных, не существует). Для этого могут потребоваться самые разнообразные приёмы, как стандартные, так и искусственные. Анализ дополнительной математической литературы показывает, что подобные задания достаточно часто встречаются в олимпиадах по математике разных лет и различных уровней, а также в задании 19 ЕГЭ по математике (профильный уровень). В то же время в школьном курсе математики данная тема практически не рассматривается, поэтому школьники, участвуя в математических олимпиадах или сдавая профильный ЕГЭ по математике, обычно сталкиваются со значительными трудностями при выполнении подобного рода заданий. В связи с этим целесообразно выделить систему основных методов решения уравнений в целых числах, тем более что в изученной математической литературе этот вопрос явно не оговаривается. Описанная проблема определила цель данной работы: выделить основные методы решения уравнений в целых числах. Для достижения поставленной цели необходимо было решить следующие задачи:

1) Проанализировать олимпиадные материалы, а также материалы профильного ЕГЭ по математике;

2) Обозначить методы решения уравнений в целых числах и выделить преобладающие;

3) Полученные результаты проиллюстрировать примерами;

4) Составить несколько тренировочных заданий по данной теме;

5) Применяя разработанные задания, определить степень готовности учащихся девятых классов МБОУ СОШ №59 к решению подобного рода задач и сделать практические выводы.

Основная часть

Анализ разнообразной математической литературы показывает, что среди методов решения уравнений в целых числах в качестве основных можно выделить следующие:

1. Представление уравнения в виде произведения нескольких множителей, равного некоторому целому числу;
2. Представление уравнения в виде суммы квадратов нескольких слагаемых, равной некоторому целому числу;
3. Использование свойств делимости, факториалов и точных квадратов;
4. Использование Малой и Великой теорем Ферма;
5. Метод бесконечного спуска;
6. Выражение одной неизвестной через другую;
7. Решение уравнения как квадратного относительно одной из неизвестных;
8. Рассмотрение остатков от деления обеих частей уравнения на некоторое число.

Сразу же нужно оговорить, что мы понимаем под основными методами решения уравнений. Основными будем называть наиболее часто применяющиеся методы, что, конечно, не исключает возможности периодического применения новых «неожиданных» приёмов. Кроме того, причём в подавляющем большинстве случаев, применяют их различные сочетания, то есть проводят комбинирование нескольких методов.
В качестве примера сочетания методов рассмотрим уравнение, предлагавшееся на ЕГЭ по математике в 2013 году (задание С6).

Задача. Решить в натуральных числах уравнение n! + 5n + 13 = k 2 .

Решение. Заметим, что оканчивается нулём при n > 4. Далее, при любых n ∈ N оканчивается либо цифрой 0, либо цифрой 5. Следовательно, при n > 4 левая часть уравнения оканчивается либо цифрой 3, либо цифрой 8. Но она же равна точному квадрату, который не может оканчиваться этими цифрами. Поэтому нужно перебрать только четыре варианта: n = 1, n = 2, n = 3, n = 4.

Значит, уравнение имеет единственное натуральное решение n = 2, k = 5.

В этой задаче использовались свойства точных квадратов, свойства факториалов, и остатки от деления обеих частей уравнения на 10.

Теперь приведём комплекс авторских задач.

Задача 1. Решить в целых числах уравнение n 2 — 4y! = 3.

Решение. Сначала перепишем исходное уравнение в виде n 2 = 4y! + 3. Если посмотреть на это соотношение с точки зрения теоремы о делении с остатком, то можно заметить, что точный квадрат, стоящий в левой части уравнения, даёт при делении на 4 остаток 3, что невозможно. Действительно, любое целое число представимо в одном из следующих четырёх видов:

Таким образом, точный квадрат при делении на 4 даёт в остатке либо 0, либо 1. Следовательно, исходное уравнение не имеет решений.

Ключевая идея – применение свойств точных квадратов.

Задача 2. Решить в целых числах уравнение 8z 2 = (t!) 2 + 2.

Решение. Непосредственная проверка показывает, что t = 0 и t = 1 не являются решениями уравнения. Если t > 1, то t! является чётным числом, то есть, оно представимо в виде t! = 2s. В таком случае уравнение можно преобразовать к виду 4z 2 = 2s 2 + 1. Однако, полученное уравнение заведомо не имеет решений, ибо в левой части стоит чётное число, а в правой – нечётное.

Ключевая идея – применение свойств факториалов.

Задача 3. Решить в целых числах уравнение x 2 + y 2 – 2x + 6y + 5 = 0.

Решение. Исходное уравнение можно переписать следующим образом: (x – 1) 2 + (y + 3) 2 = 5.

Из условия следует, что (x – 1), (y + 3) – целые числа. Следовательно, данное уравнение эквивалентно следующей совокупности:

Теперь можно выписать всевозможные целые решения уравнения.

Задача 4. Решить в целых числах уравнение zt + t – 2z = 7.

Решение. Исходное уравнение можно преобразовать к виду (z + 1) (t – 2) = 5. Числа (z + 1), (t – 2) являются целыми, поэтому имеют место следующие варианты:

Итак, уравнение имеет ровно четыре целых решения.

Ключевая идея – представление уравнения в виде произведения, равного целому числу.

Задача 5. Решить в целых числах уравнение n(n + 1) = (2k + 1)‼

Решение. Число (2k + 1)‼ нечётно при всех неотрицательных значениях k согласно определению (при отрицательных k оно вообще не определено). С другой стороны, оно равно числу n(n + 1), которое чётно при всех целых значениях k. Противоречие.

Ключевая идея – использование чётности/нечётности частей уравнения.

Задача 6. Решить в целых числах уравнение xy + x + 2y = 1.

Решение. Путём преобразований уравнение можно свести к следующему:

Данное преобразование не изменило ОДЗ неизвестных, входящих в уравнение, так как подстановка y = –1 в первоначальное уравнение приводит к абсурдному равенству –2 = 1. Согласно условию, x – целое число. Иначе говоря, тоже целое число. Но тогда число обязано быть целым. Дробь является целым числом тогда и только тогда, когда числитель делится на знаменатель. Делители числа 3: 1,3 –1, –3. Следовательно, для неизвестной возможны четыре случая: y = 0, y = 2, y = –2, y = –4. Теперь можно вычислить соответствующие значения неизвестной x. Итак, уравнение имеет ровно четыре целых решения: (–5;0), (–5;2), (1;–2), (1;–4).

Ключевая идея – выражение одной неизвестной через другую.

Задача 7. Решить в целых числах уравнение 5 m = n 2 + 2.

Решение. Если m = 0, то уравнение примет вид n 2 = –1. Оно не имеет целых решений. Если m 0. Тогда правая часть уравнения (как и левая) будет кратна 5. Но в таком случае n 2 при делении на 5 должно давать остаток 3, что невозможно (это доказывается методом перебора остатков, который был изложен при решении задачи 1). Следовательно, данное уравнение не имеет решений в целых числах.

Ключевая идея – нахождение остатков от деления обеих частей уравнения на некоторое натуральное число.

Задача 8. Решить в целых числах уравнение (x!) 4 + (y – 1) 4 = (z + 1) 4 .

Решение. Заметим, что в силу чётности показателей степеней уравнение эквивалентно следующему: (x!) 4 + |y – 1| 4 = |z + 1| 4 . Тогда x!, |y – 1|, |z + 1| – натуральные числа. Однако, согласно Великой теореме Ферма, эти натуральные числа не могут удовлетворять исходному уравнению. Таким образом, уравнение неразрешимо в целых числах.

Ключевая идея – использование Великой теоремы Ферма.

Задача 9. Решить в целых числах уравнение x 2 + 4y 2 = 16xy.

Решение. Из условия задачи следует, что x – чётное число. Тогда x 2 = 4x₁ 2 . Уравнение преобразуется к виду x₁ 2 + y 2 = 8x₁y. Отсюда вытекает, что числа x₁, y имеют одинаковую чётность. Рассмотрим два случая.

1 случай. Пусть x₁, y – нечётные числа. Тогда x₁ = 2t + 1, y = 2s + 1. Подставляя эти выражения в уравнение, получим:

Выполним соответствующие преобразования:

Сокращая обе части полученного уравнения на 2, получим?

В левой части стоит нечётное число, а в правой – чётное. Противоречие. Значит, 1 случай невозможен.

2 случай. Пусть x₁, y – чётные числа. Тогда x₁ = 2x₂ + 1, y = 2y₁. Подставляя эти значения в уравнение, получим:

Таким образом, получилось уравнение, точно такое же, как на предыдущем шаге. Исследуется оно аналогично, поэтому на следующем шаге получим уравнение и т.д. Фактически, проводя эти преобразования, опирающиеся на чётность неизвестных, мы получаем следующие разложения: . Но величины n и k не ограничены, так как на любом шаге (со сколь угодно большим номером) будем получать уравнение, эквивалентное предыдущему. То есть, данный процесс не может прекратиться. Другими словами, числа x, y бесконечно много раз делятся на 2. Но это имеет место, только при условии, что x = y = 0. Итак, уравнение имеет ровно одно целое решение (0; 0).

Ключевая идея – использование метода бесконечного спуска.

Задача 10. Решить в целых числах уравнение 5x 2 – 3xy + y 2 = 4.

Решение. Перепишем данное уравнение в виде 5x 2 – (3x)y + (y 2 – 4) = 0. Его можно рассмотреть как квадратное относительно неизвестной x. Вычислим дискриминант этого уравнения:

Для того чтобы уравнение имело решения, необходимо и достаточно, чтобы , то есть Отсюда имеем следующие возможности для y: y = 0, y = 1, y = –1, y = 2, y = –2.

Итак, уравнение имеет ровно 2 целых решения: (0;2), (0;–2).

Ключевая идея – рассмотрение уравнения как квадратного относительно одной из неизвестных.

Составленные автором задачи были использованы при проведении эксперимента, который состоял в следующем. Всем учащимся девятых классов были предложены разработанные задания с целью выявления уровня подготовки детей по данной теме. Каждому из учеников необходимо было предложить метод нахождения целочисленных решений уравнений. В эксперименте приняли участие 64 ученика. Полученные результаты представлены в таблице 1.

ТАБЛИЦА 1

Количество учащихся, справившихся с заданием (в процентах)