Уравнение нелинейной регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Парная регрессия и корреляция
1. Парная регрессия и корреляция
1.1. Понятие регрессии
Парной регрессией называется уравнение связи двух переменных у и х
где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия описывается уравнением: y = a + b × x +e .
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Примеры регрессий, нелинейных по объясняющим переменным, но ли-
нейных по оцениваемым параметрам:
· полиномы разных степеней
· равносторонняя гипербола:
Примеры регрессий, нелинейных по оцениваемым параметрам:
· степенная
· показательная
· экспоненциальная
Наиболее часто применяются следующие модели регрессий:
– прямой
– гиперболы
– параболы
– показательной функции
– степенная функция
1.2. Построение уравнения регрессии
Постановка задачи. По имеющимся данным n наблюдений за совместным
изменением двух параметров x и y <(xi,yi), i=1,2. n> необходимо определить
аналитическую зависимость ŷ=f(x), наилучшим образом описывающую данные наблюдений.
Построение уравнения регрессии осуществляется в два этапа (предполагает решение двух задач):
– спецификация модели (определение вида аналитической зависимости
– оценка параметров выбранной модели.
1.2.1. Спецификация модели
Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Применяется три основных метода выбора вида аналитической зависимости:
– графический (на основе анализа поля корреляций);
– аналитический, т. е. исходя из теории изучаемой взаимосвязи;
– экспериментальный, т. е. путем сравнения величины остаточной дисперсии Dост или средней ошибки аппроксимации , рассчитанных для различных
моделей регрессии (метод перебора).
1.2.2. Оценка параметров модели
Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.
В случае линейной регрессии параметры а и b находятся из следующей
системы нормальных уравнений метода МНК:

Можно воспользоваться готовыми формулами, которые вытекают из этой

Для нелинейных уравнений регрессии, приводимых к линейным с помощью преобразования (x, y) → (x’, y’), система нормальных уравнений имеет
вид (1.1) в преобразованных переменных x’, y’.
Коэффициент b при факторной переменной x имеет следующую интерпретацию: он показывает, на сколько изменится в среднем величина y при изменении фактора x на 1 единицу измерения.
Линеаризующее преобразование: x’ = 1/x; y’ = y.
Уравнения (1.1) и формулы (1.2) принимают вид
Линеаризующее преобразование: x’ = x; y’ = lny.
Модифицированная экспонента: 
Степенная функция:
Линеаризующее преобразование: x’ = ln x; y’ = ln y.
Показательная функция:
Линеаризующее преобразование: x’ = x; y’ = lny.

Линеаризующее преобразование: x’ = ln x; y’ = y.
Парабола второго порядка:
Парабола второго порядка имеет 3 параметра a0, a1, a2, которые определяются из системы трех уравнений
1.3. Оценка тесноты связи
Тесноту связи изучаемых явлений оценивает линейный коэффициент
парной корреляции rxy для линейной регрессии (–1 ≤ r xy ≤ 1)
и индекс корреляции ρxy для нелинейной регрессии

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации r2xy (для линейной регрессии) или индекс детерминации (для нелинейной регрессии).
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
Для оценки качества построенной модели регрессии можно использовать
показатель (коэффициент, индекс) детерминации R2 либо среднюю ошибку аппроксимации.
Чем выше показатель детерминации или чем ниже средняя ошибка аппроксимации, тем лучше модель описывает исходные данные.
Средняя ошибка аппроксимации – среднее относительное отклонение
расчетных значений от фактических
Построенное уравнение регрессии считается удовлетворительным, если
значение не превышает 10–12 %.
1.4. Оценка значимости уравнения регрессии, его коэффициентов,
Оценка значимости всего уравнения регрессии в целом осуществляется с
помощью F-критерия Фишера.
F-критерий Фишера заключается в проверке гипотезы Но о статистической незначимости уравнения регрессии. Для этого выполняется сравнение
фактического Fфакт и критического (табличного) Fтабл значений F-критерия
Fфакт определяется из соотношения значений факторной и остаточной
дисперсий, рассчитанных на одну степень свободы
где n – число единиц совокупности; m – число параметров при переменных.
Для линейной регрессии m = 1 .
Для нелинейной регрессии вместо r 2 xy используется R2.
Fтабл – максимально возможное значение критерия под влиянием случайных факторов при степенях свободы k1 = m, k2 = n – m – 1 (для линейной регрессии m = 1) и уровне значимости α.
Уровень значимости α – вероятность отвергнуть правильную гипотезу
при условии, что она верна. Обычно величина α принимается равной 0,05 или
Если Fтабл Fфакт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов линейной регрессии и линейного коэффициента парной корреляции применяется
t-критерий Стьюдента и рассчитываются доверительные интервалы каждого
Согласно t-критерию выдвигается гипотеза Н0 о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия tфакт для оцениваемых коэффициентов регрессии и коэффициента корреляции путем сопоставления их значений с величиной стандартной ошибки
Стандартные ошибки параметров линейной регрессии и коэффициента
корреляции определяются по формулам

tтабл и tфакт принимают или отвергают гипотезу Но.
tтабл – максимально возможное значение критерия под влиянием случайных факторов при данной степени свободы k = n–2 и уровне значимости α.
Связь между F-критерием Фишера (при k1 = 1; m =1) и t-критерием Стьюдента выражается равенством
Если tтабл tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования а, b или 
Значимость коэффициента детерминации R2 (индекса корреляции) определяется с помощью F-критерия Фишера. Фактическое значение критерия Fфакт определяется по формуле
Fтабл определяется из таблицы при степенях свободы k1 = 1, k2 = n–2 и при
заданном уровне значимости α. Если Fтабл
Парная нелинейная регрессия
Общий вид регрессионной модели:

Если в уравнении (1) присутствует только один фактор X, а f – нелинейная математическая функция, получим парную нелинейную модель регрессии вида
Различают два класса нелинейных регрессий:
1) регрессии, нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам;
2) регрессии, нелинейные как относительно объясняющих переменных, так и относительно оцениваемых параметров.
К первому классу относятся, например:
1) полиномы разных степеней
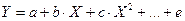
2) равносторонняя гипербола

Ко второму классу относятся:
1) степенная функция



Замечание.
Если модель второго класса с помощью соответствующих преобразований может быть приведена к линейному виду, то она называется внутренне линейной, если же модель не может быть сведена к линейной функции, то она называется внутренне нелинейной (например, 
Работа с такими моделями сводится к их предварительной линеаризации (приведению к линейному виду). Модели их первого класса приводятся к линейному виду простой заменой переменных. Для линеаризации моделей второго класса используют полулогарифмическую функцию или логарифмирование. Полученные таким образом вспомогательные линейные модели оценивают обычным МНК. Затем осуществляют обратный переход к нелинейной функции.
Пример.
Пусть зависимая переменная y – прибыль в семи различных торговых точках (исходные данные приведены в таблице 1), а фактор x – товарооборот в них.
Требуется: см. пункты 8, 9 в методичке.
Степенная модель



обозначим lg y=Y, lg x= X, и получим вспомогательную линейную модель вида
Для ее построения воспользуемся таблицей 1 (столбцы X=lg x и Y=lg y) и результатами регрессионного анализа.
| n | y | x | lg y=Y | lg x=X | yp | ei | ei^2 | eiотн | y-ycp | (y-ycp)^2 |
| 0.301 | 1.699 | 2.464 | -0.464 | 0.215 | 23.200 | -14.286 | 204.082 | |||
| 0.602 | 1.778 | 4.097 | -0.097 | 0.009 | 2.427 | -12.286 | 150.939 | |||
| 1.041 | 1.929 | 10.823 | 0.177 | 0.031 | 1.606 | -5.286 | 27.939 | |||
| 1.230 | 1.929 | 10.823 | 6.177 | 38.151 | 36.333 | 0.714 | 0.510 | |||
| 1.255 | 2.000 | 17.030 | 0.970 | 0.941 | 5.389 | 1.714 | 2.939 | |||
| 1.447 | 2.079 | 28.317 | -0.317 | 0.101 | 1.133 | 11.714 | 137.224 | |||
| 1.531 | 2.146 | 43.527 | -9.527 | 90.773 | 28.022 | 17.714 | 313.796 | |||
| Сумма | 130.222 | 98.110 | 837.429 | |||||||
| Среднее | 16.286 | 91.429 | 14.016 |
Вспомогательная линейная модель примет вид
Обратный переход к степенной функции:
Степенная модель парной регрессии примет вид:

С помощью этой модели рассчитываем все последующие столбцы таблицы 1, начиная с 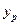
Качественные характеристики модели:

84.4 % случайной вариации переменной прибыль (y) учтено в построенной модели и обусловлено случайными колебаниями фактора оборот (х);

фактические значения прибыли отличаются от рассчитанных на основе степенной модели в среднем на 14 %;
эластичность при степенной связи переменных 


при изменении оборота на 1 % прибыль меняется в ту же сторону на 2,789%, изменение эластично.
|  |
Показательная модель

| n | y | x | lg y=Y | yp | ei | ei^2 | eiотн |
| 0.301 | 3.119 | -1.119 | 1.252 | 55.954 | |||
| 0.602 | 4.245 | -0.245 | 0.060 | 6.125 | |||
| 1.041 | 9.173 | 1.827 | 3.339 | 16.611 | |||
| 1.230 | 9.173 | 7.827 | 61.265 | 46.042 | |||
| 1.255 | 14.564 | 3.436 | 11.807 | 19.089 | |||
| 1.447 | 26.976 | 1.024 | 1.048 | 3.657 | |||
| 1.531 | 49.967 | -15.967 | 254.929 | 46.960 | |||
| Сумма | 333.700 | 194.439 | |||||
| Среднее | 16.286 | 91.429 | 27.777 |
Y=-0.161+0.0133*x – вспомогательная линейная модель.
Окончательно показательная модель примет вид:

Качественные характеристики модели:
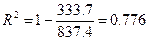
77,6 % случайной вариации переменной прибыль (y) учтено в построенной модели и обусловлено случайными колебаниями фактора оборот (х);

фактические значения прибыли отличаются от рассчитанных на основе модели в среднем на 28 %, модель неточная;
эластичность при показательной связи переменных 


при изменении оборота на 1 % прибыль меняется в ту же сторону на 2,82%, изменение эластично.
|  |
Гиперболическая модель
используем простую замену 

| n | y | x | 1/x=X | yp | ei | ei^2 | eiотн |
| 0.02 | -2.298 | 4.2983 | 18.475 | 214.9137 | |||
| 0.0167 | 5.6834 | -1.683 | 2.8338 | 42.08507 | |||
| 0.0118 | 17.421 | -6.421 | 41.231 | 58.37421 | |||
| 0.0118 | 17.421 | -0.421 | 0.1774 | 2.477429 | |||
| 0.01 | 21.647 | -3.647 | 13.299 | 20.25976 | |||
| 0.0083 | 25.638 | 2.3624 | 5.581 | 8.437161 | |||
| 0.0071 | 28.488 | 5.5118 | 30.38 | 16.21119 | |||
| Сумма | 111.98 | 362.7585 | |||||
| Среднее | 16.286 | 91.429 | 51.82265 |


Качественные характеристики модели:
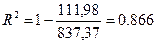
86,6 % случайной вариации переменной прибыль (y) учтено в построенной модели и обусловлено случайными колебаниями фактора оборот (х);

фактические значения прибыли отличаются от рассчитанных на основе модели в среднем на 51,8 %, модель неточная;
эластичность при гиперболической связи переменных 


при изменении оборота на 1 % прибыль меняется в ту же сторону на 1,6%, изменение эластично.
http://pandia.ru/text/78/146/82802.php
http://poisk-ru.ru/s2115t8.html





































