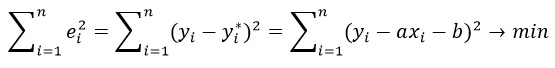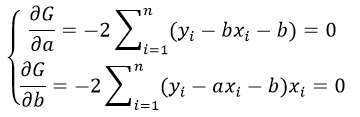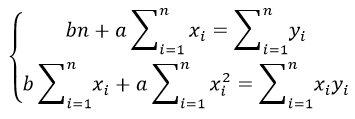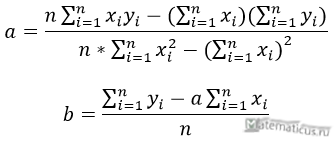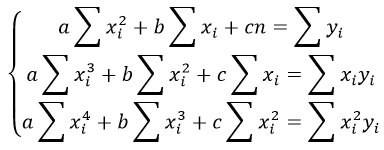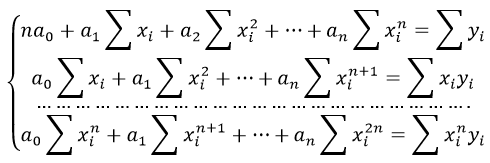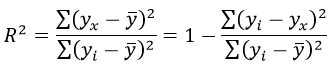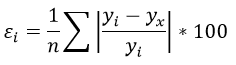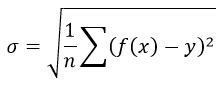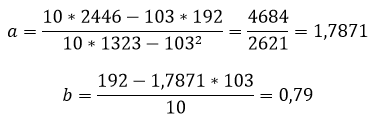Метод наименьших квадратов для нелинейных регрессионных моделей
Метод наименьших квадратов можно применять к нелинейным регрессионным моделям только в том случае, если возможна их линеаризация, т.е. они нелинейны по факторным переменным или нелинейны по параметрам, но внутренне линейны.
Рассмотрим применение МНК для определения неизвестных параметров уравнения параболической зависимости следующего вида:
Данный полином второго порядка (или второй степени) является нелинейным по факторным переменным xi . Для нахождения неизвестных параметров уравнения регрессии β0 , β1 , β2 необходимо минимизировать с помощью МНК функцию Q:
Процесс минимизации функции сводится к вычислению частных производных этой функции по каждому из оцениваемых параметров. Составим систему уравнений для данной функции Q, не пользуясь при этом методом замен:




После элементарных преобразований данной системы уравнений получим
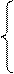
Данная система является системой нормальных уравнений относительно параметров β0, β1 , β2 для параболической зависимости yi = β0 + β1xi + β2x 2 i + εi . Эта система является квадратной, т.е. количество уравнений равняется количеству неизвестных переменных. Коэффициенты β0 , β1 , β2 можно найти с помощью метода Гаусса, если свести систему нормальных уравнений к линейному виду с помощью метода замен.
В общем случае полинома п-й степени
Для нахождения неизвестных коэффициентов уравнения регрессии с помощью МНКнеобходимо минимизировать функцию Q следующего вида:
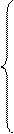
Решением данной системы будут являться оценки коэффициентов регрессионной зависимости, выраженной полиномом п-го порядка.
Метод Гаусса применяется в большинстве случаев для решения систем линейных уравнений, когда число неизвестных параметров не совпадает с количеством уравнений. Однако его используют и для решения квадратных систем линейных уравнений.
Основная идея решения системы линейных уравнений методом Гаусса заключается в том, что исходную систему из т линейных уравнений с п неизвестными переменными необходимо преобразовать к треугольному виду. Для этого в одном из уравнений системы оставляют все неизвестные переменные. В другом сокращают одну из неизвестных переменных для того, чтобы их число стало (п — 1). В следующем уравнении убирают две неизвестные переменные, чтобы их число уже было (п — 2). В конце данного процесса система примет треугольный вид: первое уравнение содержит все, а последнее — только (п — т) неизвестных, которые называются базисными. Остальные переменные называются свободными. Дальнейшее решение сводится к выражению свободных неизвестных переменных через базисные и получению общего решения системы линейных уравнений. Для осуществления базисного решения системы линейных уравнений свободные переменные приравнивают к нулю.
Дата добавления: 2015-10-05 ; просмотров: 2619 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Метод наименьших квадратов регрессия
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R 2 :
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:
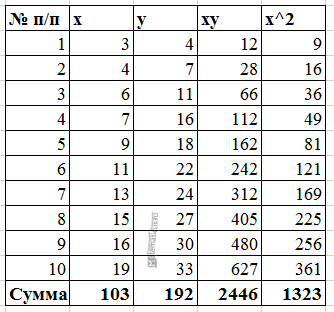
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
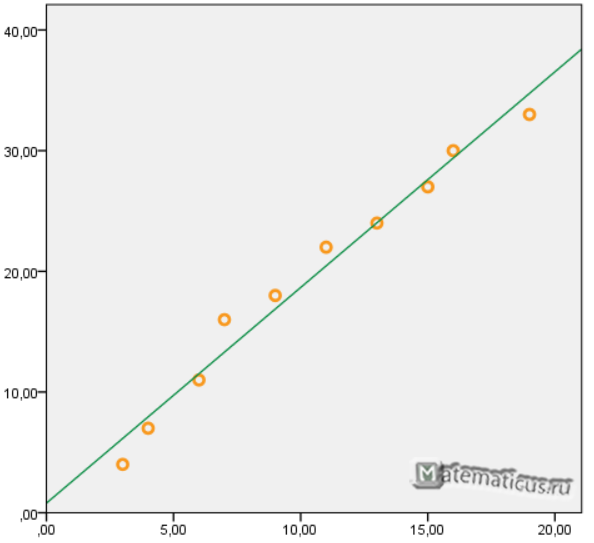
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Уравнение нелинейной регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
http://www.matematicus.ru/matematicheskaya-statistika/metod-naimenshih-kvadratov-regressiya
http://math.semestr.ru/corel/noncorel.php