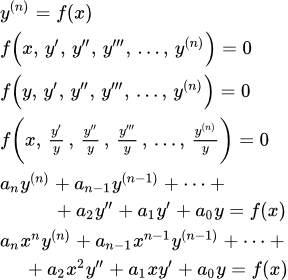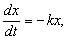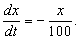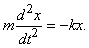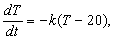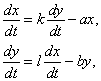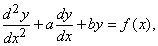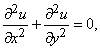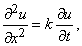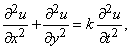Нелинейные дифференциальные уравнения высшего порядка

Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Уравнения, содержащие переменную и старшую производную

Разрешенные относительно старшей производной

Рассмотрим дифференциальное уравнение следующего вида:
.
Интегрируем n раз.
;
;
и так далее. Так же можно использовать формулу:
.
См. Дифференциальные уравнения, решающиеся непосредственным интегрированием

Разрешенные относительно переменной

Рассмотрим дифференциальное уравнение, в котором независимая переменная x является функцией от старшей производной:
.
Это уравнение можно решить параметрическим методом. Для этого вводим параметр . В результате получаем:
;
.
Из последнего уравнения . Интегрируя, получаем зависимость производной от x в параметрическом виде:
.
Продолжая интегрирование аналогичным образом, получим зависимость y от x в параметрическом виде.

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только независимую переменную и старшую производную общего вида:
.
Его можно решить в квадратурах в параметрическом виде, если удастся подобрать такие функции и , для которых .

Если такие функции найдены, то положим . Тогда исходное уравнение выполняется автоматически. Дифференцируя первую функцию, находим связь между дифференциалами переменных x и t : . Тогда
.
Интегрируя последнее соотношение, получаем решение для производной более низкого порядка в параметрическом виде. Продолжая действовать подобным способом, получим общее решение в квадратурах.

Уравнения, содержащие только производные порядков n и n-1

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Тогда положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению .

Тогда
;
.
Интегрируя эти уравнения, получим параметрическое представление производной порядка n – 2 . Продолжая подобным образом, получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Уравнения, содержащие только производные порядков n и n-2

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению.

Тогда
;
;
;
;
.
Интегрируя, получим параметрическое представление производных порядка n, n – 1 и n – 2 . Далее интегрируем как в предыдущем случае ⇑. В результате получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Дифференциальные уравнения высших порядков, допускающие понижение порядка

Уравнения, не содержащие зависимую переменную y в явном виде

Подстановка приводит к понижению порядка уравнения на единицу. Здесь – функция от .
См. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

Уравнения, не содержащие независимую переменную x в явном виде

Для решения этого уравнения, делаем подстановку
.
Считаем, что является функцией от . Тогда
.
Аналогично для остальных производных. В результате порядок уравнения понижается на единицу.
См. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде

Однородные дифференциальные уравнения высших порядков

Уравнения, однородные относительно функции и ее производных

Дифференциальное уравнение

является однородным относительно функции и ее производных, если оно обладает свойством:
.
Здесь t – число или любая функция; число p называют показателем однородности.

Чтобы распознать такое уравнение, нужно сделать замену
.
Если после преобразований t сократится, то это однородное уравнение.

Для его решения делаем подстановку
,
где – функция от . Тогда
.
Аналогично преобразуем производные и т.д. В результате порядок уравнения понижается на единицу.
См. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков

Обобщенно однородные уравнения относительно переменных

Теперь рассмотрим дифференциальные уравнения, которые не меняют вида, если сделать замену переменных: , где c – постоянная; s – измерение однородности для переменной y. При такой замене производная порядка m умножается на :
.
Если записать исходное уравнение в общем виде:
,
то оно является обобщенно однородным относительно переменных, если обладает свойством:
,
где t – число или любая функция; p – показатель однородности.

При подобные уравнения можно назвать однородными дифференциальными уравнениями относительно переменных.

Порядок такого уравнения можно понизить на единицу, если искать решение в параметрическом виде, и перейти от зависимой переменной (функции) y к новой зависимой переменной (новой функции) с помощью подстановок:
, где t – параметр.
В результате для функции получим дифференциальное уравнение n — го порядка, которое не содержит переменную t в явном виде. Далее понижаем порядок изложенным выше методом ⇑.
См. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков

Дифференциальные уравнения с полной производной

Это уравнения, которые можно привести к полной производной:
.
Отсюда сразу получаем первый интеграл:
.
Он представляет собой дифференциальное уравнение, на единицу меньшего порядка по сравнению с исходным уравнением .

В качестве примера рассмотрим дифференциальное уравнение второго порядка:
.
Разделим его на . Тогда
.
Отсюда получаем первый интеграл, который является дифференциальным уравнением первого порядка:
.
См. Дифференциальные уравнения высших порядков с полной производной.

Линейные дифференциальные уравнения высших порядков

Рассмотрим линейное однородное дифференциальное уравнение n-го порядка:
(1) ,
где – функции от независимой переменной . Пусть есть n линейно независимых решений этого уравнения. Тогда общее решение уравнения (1) имеет вид:
(2) ,
где – произвольные постоянные. Сами функции образуют фундаментальную систему решений.
Фундаментальная система решений линейного однородного уравнения n-го порядка – это n линейно независимых решений этого уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка:
.
Пусть есть частное (любое) решение этого уравнения. Тогда общее решение имеет вид:
,
где – общее решение однородного уравнения (1).

Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним

Линейные однородные уравнения с постоянными коэффициентами

Это уравнения вида:
(3) .
Здесь – действительные числа. Чтобы найти общее решение этого уравнения, нам нужно найти n линейно независимых решений , которые образуют фундаментальную систему решений. Тогда общее решение определяется по формуле (2):
(2) .

Ищем решение в виде . Получаем характеристическое уравнение:
(4) .

Если это уравнение имеет различные корни , то фундаментальная система решений имеет вид:
.

Если имеется комплексный корень
,
то существует и комплексно сопряженный корень . Этим двум корням соответствуют решения и , которые включаем в фундаментальную систему вместо комплексных решений и .

Кратным корням кратности соответствуют линейно независимых решений: .

Кратным комплексным корням кратности и их комплексно сопряженным значениям соответствуют линейно независимых решений:
.

Линейные неоднородные уравнения со специальной неоднородной частью

Рассмотрим уравнение вида
,
где – многочлены степеней s 1 и s 2 ; – постоянные.

Сначала мы ищем общее решение однородного уравнения (3). Если характеристическое уравнение (4) не содержит корень , то ищем частное решение в виде:
,
где
;
;
s – наибольшее из s 1 и s 2 .

Если характеристическое уравнение (4) имеет корень кратности , то ищем частное решение в виде:
.

После этого получаем общее решение:
.

Линейные неоднородные уравнения с постоянными коэффициентами

Здесь возможны три способа решения.

1) Метод Бернулли.
Сначала находим любое, отличное от нуля, решение однородного уравнения
.
Затем делаем подстановку
,
где – функция от переменной x . Получаем дифференциальное уравнение для u , которое содержит только производные от u по x . Выполняя подстановку , получаем уравнение n – 1 — го порядка.

2) Метод линейной подстановки.
Сделаем подстановку
,
где – один из корней характеристического уравнения (4). В результате получим линейное неоднородное уравнение с постоянными коэффициентами порядка . Последовательно применяя такую подстановку, приведем исходное уравнение к уравнению первого порядка.

3) Метод вариации постоянных Лагранжа.
В этом методе мы сначала решаем однородное уравнение (3). Его решение имеет вид:
(2) .
Далее мы считаем, что постоянные являются функциями от переменной x . Тогда решение исходного уравнения имеет вид:
,
где – неизвестные функции. Подставляя в исходное уравнение и накладывая на некоторые ограничения, получаем уравнения, из которых можно найти вид функций .

Уравнение Эйлера

Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
.
Однако, для решения уравнения Эйлера, делать такую подстановку нет необходимости. Можно сразу искать решение однородного уравнения в виде
.
В результате получим такие же правила, как и для уравнения с постоянными коэффициентами, в которых вместо переменной нужно подставить .

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 13-06-2017 Изменено: 11-05-2021

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость – производная от расстояния; аналогично, ускорение – производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).

Примеры.

Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений.

1) Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x – количество вещества в некоторый момент времени t, то этот закон можно записать так:

где dx/dt – скорость распада, а k – некоторая положительная постоянная, характеризующая данное вещество. (Знак «минус» в правой части указывает на то, что x убывает со временем; знак «плюс», подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.)

2) Емкость первоначально содержит 10 кг соли, растворенной в 100 м 3 воды. Если чистая вода вливается в емкость со скоростью 1 м 3 в минуту и равномерно перемешивается с раствором, а образовавшийся раствор вытекает из емкости с такой же скоростью, то сколько соли окажется в емкости в любой последующий момент времени? Если x – количество соли (в кг) в емкости в момент времени t, то в любой момент времени t в 1 м 3 раствора в емкости содержится x/100 кг соли; поэтому количество соли убывает со скоростью x/100 кг/мин, или

3) Пусть на тело массы m, подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть x – величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от x по времени, обозначаемая d 2 x/dt 2 ) пропорционально силе:

Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины.

4) Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то

где T – температура кофе в момент времени t.

5) Министр иностранных дел государства Блефуску утверждает, что принятая Лиллипутией программа вооружений вынуждает его страну увеличить военные расходы на сколько это только возможно. С аналогичными заявлениями выступает и министр иностранных дел Лиллипутии. Возникающую в результате ситуацию (в простейшей интерпретации) можно точно описать двумя дифференциальными уравнениями. Пусть x и y – расходы на вооружение Лиллипутии и Блефуску. Предполагая, что Лиллипутия увеличивает свои расходы на вооружение со скоростью, пропорциональной скорости увеличения расходов на вооружение Блефуску, и наоборот, получаем:

где члены —ax и —by описывают военные расходы каждой из стран, k и l – положительные постоянные. (Эту задачу впервые таким образом сформулировал в 1939 Л.Ричардсон.)

После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины, скорости изменения которых входят в уравнения. Иногда решения находятся в виде явных формул, но чаще их удается представить лишь в приближенном виде или же получить о них качественную информацию. Часто бывает трудно установить, существует ли решение вообще, не говоря уже о том, чтобы найти его. Важный раздел теории дифференциальных уравнений составляют так называемые «теоремы существования», в которых доказывается наличие решения у того или иного типа дифференциальных уравнений.

Первоначальная математическая формулировка физической задачи обычно содержит упрощающие предположения; критерием их разумности может служить степень согласованности математического решения с имеющимися наблюдениями.

Решения дифференциальных уравнений.

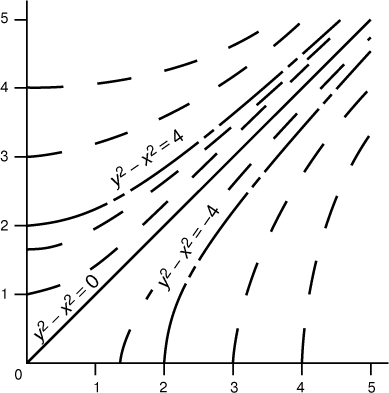
Дифференциальному уравнению, например dy/dx = x/y, удовлетворяет не число, а функция, в данном конкретном случае такая, что ее график в любой точке, например в точке с координатами (2,3), имеет касательную с угловым коэффициентом, равным отношению координат (в нашем примере 2/3). В этом нетрудно убедиться, если построить большое число точек и от каждой отложить короткий отрезок с соответствующим наклоном. Решением будет функция, график которой касается каждой своей точкой соответствующего отрезка. Если точек и отрезков достаточно много, то мы можем приближенно наметить ход кривых-решений (три такие кривые показаны на рис. 1). Существует ровно одна кривая-решение, проходящая через каждую точку с y № 0. Каждое отдельное решение называется частным решением дифференциального уравнения; если удается найти формулу, содержащую все частные решения (за исключением, быть может, нескольких особых), то говорят, что получено общее решение. Частное решение представляет собой одну функцию, в то время как общее – целое их семейство. Решить дифференциальное уравнение – это значит найти либо его частное, либо общее решение. В рассматриваемом нами примере общее решение имеет вид y 2 – x 2 = c, где c – любое число; частное решение, проходящее через точку (1,1), имеет вид y = x и получается при c = 0; частное решение, проходящее через точку (2,1), имеет вид y 2 – x 2 = 3. Условие, требующее, чтобы кривая-решение проходила, например, через точку (2,1), называется начальным условием (так как задает начальную точку на кривой-решении).

Можно показать, что в примере (1) общее решение имеет вид x = ce –kt , где c – постоянная, которую можно определить, например, указав количество вещества при t = 0. Уравнение из примера (2) – частный случай уравнения из примера (1), соответствующий k = 1/100. Начальное условие x = 10 при t = 0 дает частное решение x = 10e –t/100 . Уравнение из примера (4) имеет общее решение T = 70 + ce –kt и частное решение 70 + 130 –kt ; чтобы определить значение k, необходимы дополнительные данные.

Дифференциальное уравнение dy/dx = x/y называется уравнением первого порядка, так как содержит первую производную (порядком дифференциального уравнения принято считать порядок входящей в него самой старшей производной). У большинства (хотя и не у всех) возникающих на практике дифференциальных уравнений первого рода через каждую точку проходит только одна кривая-решение.

Существует несколько важных типов дифференциальных уравнений первого порядка, допускающих решения в виде формул, содержащих только элементарные функции – степени, экспоненты, логарифмы, синусы и косинусы и т.д. К числу таких уравнений относятся следующие.

Уравнения с разделяющимися переменными.

Уравнения вида dy/dx = f(x)/g(y) можно решить, записав его в дифференциалах g(y)dy = f(x)dx и проинтегрировав обе части. В худшем случае решение представимо в виде интегралов от известных функций. Например, в случае уравнения dy/dx = x/y имеем f(x) = x, g(y) = y. Записав его в виде ydy = xdx и проинтегрировав, получим y 2 = x 2 + c. К уравнениям с разделяющимися переменными относятся уравнения из примеров (1), (2), (4) (их можно решить описанным выше способом).

Уравнения в полных дифференциалах.

Если дифференциальное уравнение имеет вид dy/dx = M(x,y)/N(x,y), где M и N – две заданные функции, то его можно представить как M(x,y)dx – N(x,y)dy = 0. Если левая часть является дифференциалом некоторой функции F(x,y), то дифференциальное уравнение можно записать в виде dF(x,y) = 0, что эквивалентно уравнению F(x,y) = const. Таким образом, кривые-решения уравнения – это «линии постоянных уровней» функции, или геометрические места точек, удовлетворяющих уравнениям F(x,y) = c. Уравнение ydy = xdx (рис. 1) – с разделяющимися переменными, и оно же – в полных дифференциалах: чтобы убедиться в последнем, запишем его в виде ydy – xdx = 0, т.е. d(y 2 – x 2 ) = 0. Функция F(x,y) в этом случае равна (1/2)(y 2 – x 2 ); некоторые из ее линий постоянного уровня представлены на рис. 1.

Линейные уравнения.

Линейные уравнения – это уравнения «первой степени» – неизвестная функция и ее производные входят в такие уравнения только в первой степени. Таким образом, линейное дифференциальное уравнение первого порядка имеет вид dy/dx + p(x) = q(x), где p(x) и q(x) – функции, зависящие только от x. Его решение всегда можно записать с помощью интегралов от известных функций. Многие другие типы дифференциальных уравнений первого порядка решаются с помощью специальных приемов.

Уравнения старших порядков.

Многие дифференциальные уравнения, с которыми сталкиваются физики, это уравнения второго порядка (т.е. уравнения, содержащие вторые производные) Таково, например, уравнение простого гармонического движения из примера (3), md 2 x/dt 2 = –kx. Вообще говоря, можно ожидать, что уравнение второго порядка имеет частные решения, удовлетворяющие двум условиям; например, можно потребовать, чтобы кривая-решение проходила через данную точку в данном направлении. В случаях, когда дифференциальное уравнение содержит некоторый параметр (число, величина которого зависит от обстоятельств), решения требуемого типа существуют только при определенных значениях этого параметра. Например, рассмотрим уравнение md 2 x/dt 2 = –kx и потребуем, чтобы y(0) = y(1) = 0. Функция y є 0 заведомо является решением, но если 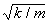– целое кратное числа p, т.е. k = m 2 n 2 p2, где n – целое число, а в действительности только в этом случае, существуют другие решения, а именно: y = sin npx. Значения параметра, при которых уравнение имеет особые решения, называются характеристическими или собственными значениями; они играют важную роль во многих задачах.

Уравнение простого гармонического движения служит примером важного класса уравнений, а именно: линейных дифференциальных уравнений с постоянными коэффициентами. Более общий пример (также второго порядка) – уравнение

где a и b – заданные постоянные, f(x) – заданная функция. Такие уравнения можно решать различными способами, например, с помощью интегрального преобразования Лапласа. То же можно сказать и о линейных уравнениях более высоких порядков с постоянными коэффициентами. Не малую роль играют также и линейные уравнения с переменными коэффициентами.

Нелинейные дифференциальные уравнения.

Уравнения, содержащие неизвестные функции и их производные в степени выше первой или каким-либо более сложным образом, называются нелинейными. В последние годы они привлекают все большее внимание. Дело в том, что физические уравнения обычно линейны лишь в первом приближении; дальнейшее и более точное исследование, как правило, требует использования нелинейных уравнений. Кроме того, многие задачи нелинейны по своей сути. Так как решения нелинейных уравнений зачастую очень сложны и их трудно представить простыми формулами, значительная часть современной теории посвящена качественному анализу их поведения, т.е. разработке методов, позволяющих, не решая уравнения, сказать нечто существенное о характере решений в целом: например, что все они ограниченны, или имеют периодический характер, или определенным образом зависят от коэффициентов.

Приближенные решения дифференциальных уравнений могут быть найдены в численном виде, но для этого требуется много времени. С появлением быстродействующих компьютеров это время сильно сократилось, что открыло новые возможности численного решения многих, ранее не поддававшихся такому решению, задач.

Теоремы существования.

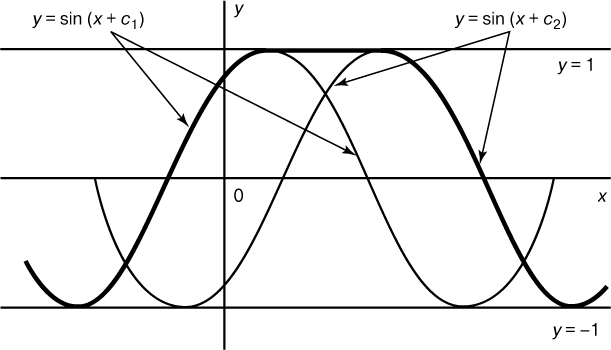
Теоремой существования называется теорема, утверждающая, что при определенных условиях данное дифференциальное уравнение имеет решение. Встречаются дифференциальные уравнения, не имеющие решений или имеющие их больше, чем ожидается. Назначение теоремы существования – убедить нас в том, что у данного уравнения действительно есть решение, а чаще всего заверить, что оно имеет ровно одно решение требуемого типа. Например, уже встречавшееся нам уравнение dy/dx = –2y имеет ровно одно решение, проходящее через каждую точку плоскости (x,y), а так как одно такое решение мы уже нашли, то тем самым полностью решили это уравнение. С другой стороны, уравнение (dy/dx) 2 = 1 – y 2 имеет много решений. Среди них прямые y = 1, y = –1 и кривые y = sin(x + c). Решение может состоять из нескольких отрезков этих прямых и кривых, переходящих друг в друга в точках касания (рис. 2).

Дифференциальные уравнения в частных производных.

Обыкновенное дифференциальное уравнение – это некоторое утверждение о производной неизвестной функции одной переменной. Дифференциальное уравнение в частных производных содержит функцию двух или более переменных и производные от этой функции по крайней мере по двум различных переменным.

В физике примерами таких уравнений являются уравнение Лапласа

где, согласно одной из возможных интерпретаций, u – температура в плоской области, точки которой задаются координатами x и y; уравнение теплопроводности

где t – время, x – расстояние от одного из концов однородного стержня, по которому распространяется тепловой поток; и волновое уравнение

где t – снова время, x и y – координаты точки колеблющейся струны.

Решая дифференциальные уравнения в частных производных, обычно не стремятся найти общее решение, поскольку оно скорее всего окажется слишком общим, чтобы быть полезным. Если решение обыкновенного дифференциального уравнения определяется заданием условий в одной или нескольких точках; то решение дифференциального уравнения в частных производных обычно определяется заданием условий на одной или нескольких кривых. Например, решение уравнения Лапласа может быть найдено в точке (x, y) внутри круга, если значения u заданы в каждой точке ограничивающей окружности. Поскольку проблемы с более чем одной переменной в физике являются скорее правилом, чем исключением, легко представить, сколь обширен предмет теории дифференциальных уравнений в частных производных.

Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1977
Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М., 1982
Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., 1984
Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями. М., 1986

НЕЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

Перов А. И. 1 , Каверина В.К. 2

1 Доктор физико-математических наук, Воронежский государственный университет, 2 Кандидат физико-математических наук, Воронежский государственный архитектурно-строительный университет

Работа выполнена при поддержке гранта РФФИ №16-01-00197

НЕЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

Аннотация

В статье изучается вопрос существования периодических решений у возмущенного дифференциального уравнения -го порядка. Полученные теоремы навеяны проблемой В.И. Зубова и связаны с понятиями асимптотической устойчивости в целом и устойчивости по Дирихле. Доказательства этих теорем носят топологический характер и опираются на понятие степени отображения.

Ключевые слова: нелинейные скалярные дифференциальные уравнения высшего порядка, периодические решения (свободные и вынужденные колебания), топологическая степень отображения, метод направляющих функций.

Perov A. I. 1 , Kaverina V. K. 2

1 PhD in Physics and Mathematics, Voronezh State University, 2 PhD in Physics and Mathematics, Voronezh State University of Architecture and Civil Engineering

NON-LINEAR DIFFERENTIAL EQUATIONS OF HIGHER ORDER

Abstract

In this article we study the problem of the existence of periodic solutions of the perturbed differential equations of higher order. These theorems were inspired by the work of V.I. Zubov and associated with such notions as asymptotically stability in the large and stability in the Dirichlet’s sense in the large. Proofs of these theorems have a topological sense.

Keywords: nonlinear scalar differential equations of higher order, periodic solutions (free and forced oscillations), topological degree of mapping, method of guiding functions.