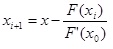Нелинейные уравнения с одним неизвестным могут быть

Решение нелинейного уравнения с одним неизвестным в различных средах программного обеспечения

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Волжский государственный инженерно-педагогический университет»

Кафедра математики и информатики

Решение нелинейного уравнения с одним неизвестным в различных средах программного обеспечения

Методическая разработка по выполнению курсовой работы по информатике для студентов специальности 080801.65 – Прикладная информатика (в менеджменте)

1.Постановка задачи 4

2.Методы отделения корней 5

2.1.Графический метод 5

2.2Аналитический метод 6

3.Методы уточнения корней 8

3.1.Метод половинного деления 8

3.2.Метод последовательных приближений 10

3.3.Метод Ньютона 12

4.Анализ результатов 16

Варианты заданий 18

Список рекомендуемой литературы 19

В настоящее время появилось значительное число различных программных продуктов (MathCad, Mathlab и т. д.), с помощью которых, задавая только входные данные и не вникая в сущность алгоритмов, можно решить значительное число задач. Безусловно, умение пользоваться этими программными продуктами существенно сокращает время и ресурсы по решению ряда важных задач.

Зачастую решение некоторых задач сводится к решению достаточно сложных нелинейных уравнений, которые могут представлять собой самостоятельную задачу или являться составной частью более сложных задач. Корни таких уравнений сравнительно редко удается найти точными методами. Кроме того, в некоторых случаях коэффициенты уравнения, полученные в процессе эксперимента или как результаты предварительных расчетов, известны лишь приблизительно. Значит, сама задача о точном определении корней уравнения теряет смысл, и важное значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности. При традиционном подходе к изучению численных методов в основном в математических курсах ориентируются на стандартные ручные расчеты. С развитием материальной и программной базы современных компьютеров при принятии тех или иных решений более реалистичным представляется подход численных расчетов при использовании новейших информационных технологий.

В представленной работе на примере решения нелинейного уравнения с одной неизвестной f(x)=x++-2.5 реализуются 3 технологии:

● алгоритмическая на базе программной среды Pascal;

● с использованием табличного процессора Excel;

● на основе пакета формульных преобразований MathCAD.

Делается сравнительный анализ полученных результатов.

Пусть дано уравнение f (x)=0, (1) где функция f (x) непрерывна на некотором множестве X.

Совокупность значений переменной х, при которых уравнение (1) обращается в тождество, называется решением этого уравнения, а каждое отдельное значение – корнем уравнения. В зависимости от вида функции f(x) уравнения подразделяются на алгебраические и трансцендентные.

В первых для получения значения функции по аргументу необходимо выполнить арифметические операции и возведение в степень с рациональным показателем (иррациональные функции, где используется операция извлечения корня, также относят к классу алгебраических функций).

Алгебраическое уравнение можно привести к виду:

++…++=0, (2) где числа , i = — коэффициенты уравнения, которые в общем случае являются комплексными.

Таким образом, корни уравнения могут быть как вещественными, так и комплексными. Будем считать числа вещественными.

Функцию называют трансцендентной, если она содержит логарифмические, показательные, тригонометрические и другие функции. И если в записи уравнения (1) содержится трансцендентная функция, то уравнение называют трансцендентным.

Точные аналитические значения корней уравнения (1) можно найти лишь в простейших случаях (ах+в=0; а+вх+с=0; соs(x)=а и т. д.). Кроме того, коэффициенты некоторых уравнений есть приближенные числа, поэтому нельзя говорить о нахождении точных корней.

Будем считать, что уравнение (1) имеет только действительные корни. Тогда нахождение корней с заданной точностью необходимо проводить в два этапа:

отделение корней, т. е. нахождение достаточно малых промежутков, в которых содержится только один корень уравнения; уточнение каждого из отдельных корней, т. е. определение их с заданной точностью.

Рассмотрим технологию выполнения курсовой работы на примере определения корней уравнений на интервале .

Методы отделения (локализации) корней Графический метод

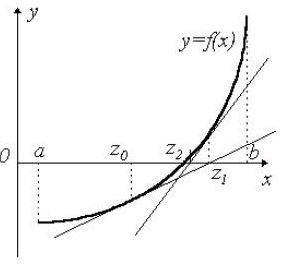
Он основан на построении графика функции y=f(x). Тогда искомым отрезком [а;в], содержащим корень уравнения (1), будет отрезок оси абсцисс, содержащий точку пересечения графика с этой осью. Иногда выгоднее представить исходную функцию в виде разности двух более простых функций f(x)=g(x)-g1(x) и строить два графика = g(x) и = g1(x), точка пересечения которых и является корнем уравнения (1), а отрезок на оси абсцисс с корнем внутри и будет являться интервалом изоляции. Этот метод хорошо работает в случае, если исходное уравнение не имеет близких корней и дает тем точнее результат, чем мельче берется сетка по оси ОХ.

Первый способ f(x) = x++-2.5

Второй способ g(x) = x+; g1(x) = 2.5 —

Искомый корень уравнения находится на отрезке [0,7;0,8]

Аналитический метод основан на следующем положении: если непрерывная и дифференцируемая на отрезке [a;b] функция f(x) принимает значения разных знаков на его концах (т. е. f(a)∙f(b) 0 . Тогда функцию ц(x) можно представить как ц(x) = x — л∙F(x). Затем, варьируя параметр л, добиваемся условия сходимости: |ц’(x)|

Уравнения с одним неизвестным. Вводные замечания

Задача нахождения корней нелинейных уравнений вида

встречается в различных областях научных исследований (здесь F(x) – некоторая непрерывная функция). Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическимиуравнениями называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие (не алгебраические) функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными.

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямыеметоды – методы, которые позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры читателю известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Однако встречающиеся на практике уравнения часто не удается решить такими простыми методами. Для их решения используются итерационныеметоды, т.е. методы последовательных приближений. Алгоритм нахождения корня нелинейного уравнения с помощью итерационного метода состоит из двух этапов: а) отыскания приближенного значения корня (начального приближения); б) уточнения приближенного значения до некоторой заданной степени точности. В некоторых методах отыскивается не начальное приближение, а некоторый отрезок, содержащий корень.

Начальное приближение может быть найдено различными способами: из физических соображений, из решения аналогичной задачи при других исходных данных, с помощью графических методов. Если такие априорные оценки исходного приближения провести не удается, то находят две близко расположенные точки а и b, в которых непрерывная функция F(x) принимает значения разных знаков, т.е. F(a)F(b) Будет полезно почитать по теме:

Решение нелинейных уравнений

Уравнения, в которых содержатся неизвестные функции, произведенные в степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение, х^3 – 0,2x^2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).

Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.

Существует множество методов решения нелинейных уравнений и систем нелинейных уравнений, которые принято относить в 3 группы: численные, графические и аналитические. Аналитические методы позволяют определить точные значения решения уравнений. Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений. Численное решение нелинейных уравнений предполагает прохождения двух этапов: отделение корня и его уточнение до определенно заданной точности.
Отделение корней осуществляется различными способами: графически, при помощи различных специализированных компьютерных программ и др.

Рассмотрим несколько методов уточнения корней с определенно заданной точностью.

Методы численного решения нелинейных уравнений

Метод половинного деления.

Суть метода половинного деления заключается в делении интервала [a,b] пополам (с=(a+b)/2) и отбрасывании той части интервала, в которой отсутствует корень, т.е. условие F(a)xF(b)

Рис.1. Использование метода половинного деления при решении нелинейных уравнений.

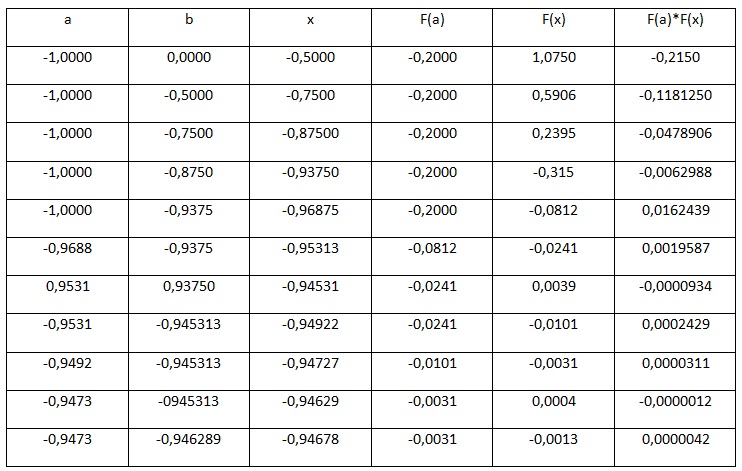
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0, то начала отрезка a переносится в x (a=x), иначе, конец отрезка b переносится в точку x (b=x). Полученный отрезок делим опять пополам и т.д. Весь произведенный расчет отражен ниже в таблице.

Рис.2. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

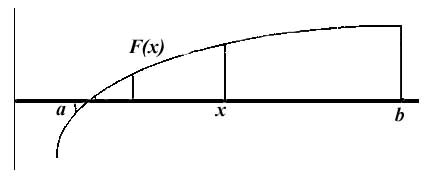
При использовании метода хорд, задается отрезок [a,b], в котором есть только один корень с установленной точностью e. Через точки в отрезке a и b, которые имеют координаты (x(F(a);y(F(b)), проводится линия (хорда). Далее определяются точки пересечения этой линии с осью абсцисс (точка z).
Если F(a)xF(z)

Рис.3. Использование метода хорд при решении нелинейных уравнений.

Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0;

Определим вторую производную F’’(x) = 6x-0,4.

F’’(-1)=-6,4 0 соблюдается, поэтому для определения корня уравнения воспользуемся формулой:

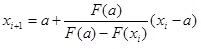
, где x0=b, F(a)=F(-1)=-0,2

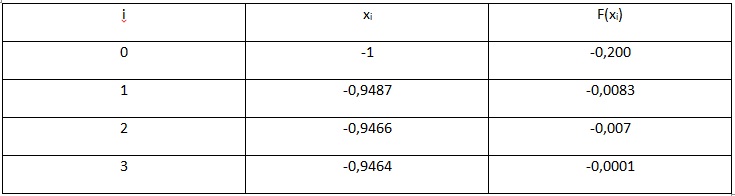
Весь произведенный расчет отражен ниже в таблице.

Рис.4. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

Метод касательных (Ньютона)

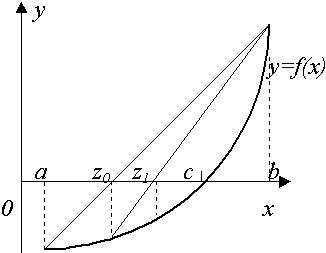
Данный метод основывается на построении касательных к графику, которые проводятся на одном из концов интервала [a,b]. В точке пересечения с осью X (z1) строится новая касательная. Данная процедура продолжается до тех пор, пока полученное значение не будет сравним с нужным параметром точности e (F(zi)

Рис.5. Использование метода касательных (Ньютона) при решении нелинейных уравнений.

Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0 выполняется, поэтому расчеты производим по формуле:

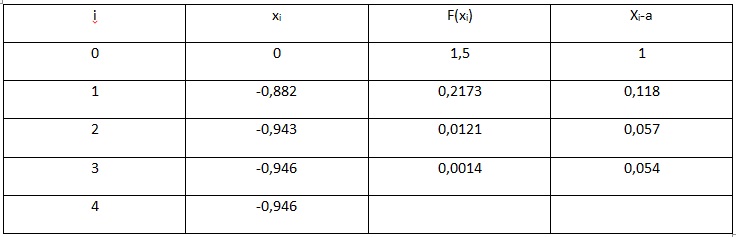
Весь произведенный расчет отражен ниже в таблице.

Рис.6. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях: