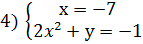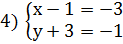Нелинейные уравнения в целых числах

Метод решения относительно одной переменной

Методы решения нелинейных уравнений и неравенств в целых числах

При решении нелинейных уравнений в целых и натуральных числах можно условно выделить следующие методы:

1. Метод разложения на множители;

2. Метод решения относительно одной переменной;

4. Метод остатков;

6. Метод доказательства от противного;

7. Метод параметризации уравнения;

8. Функционально-графический метод.

Метод разложения на множители

· Вынесение общих множителей за скобку.

Задание 1. Решить в целых числах уравнение 2х 3 +ху-7=0

Решение: Приведем уравнение к виду: х(2х 2 +у)=7. Так как , то рассмотрим четыре системы уравнений:

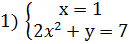
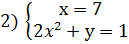
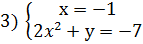
Из каждой системы получаем решения.

· Применение формул сокращенного умножения.

Задание 2. Найти все пары натуральных чисел, разность квадратов которых равна 55.

Решение: Запишем условие задачи в виде уравнения n 2 -k 2 =55 или (n-k)(n+k)=55. Так как (n+k)>0, то (n-k)>0, причем (n+k)>(n-k). Поскольку , то возможны только два случая:

. Из каждой системы получаем решения

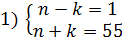
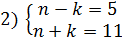
Задание 3. Решить в целых числах уравнение ху+3х-у=6..

Задание 3. Решить в целых числах уравнение ху+3х-у=6.

Решение: Запишем уравнение в виде х(у+3)-(у+3)=3 или (х-1)(у+3)=3. Так как , то рассмотрим четыре системы

Из каждой системы получаем решения.

Разложение квадратного трехчлена.

Задание 4. Решить в целых числах уравнение х 2 -3ху+2у 2 =11.

Решение: решим квадратное уравнение х 2 -3ху+2у 2 =11 относительно переменной х: х₁=у и х₂=2у. Тогда получаем: (х-у)(х-2у)=11. Так как … (продолжи решение)

Задание 5. Решить в целых числах уравнение 2х 2 -2ху++9х+у=2.

Решение: Перепишем уравнение в виде 2х 2 -х(2у-9)+у-2+а=аи разложим левую часть уравнения на множители как квадратный трехчлен относительно х. Найдем дискриминант D=4у 2 -44у+97-8а. Очевидно, если 97-8а=121, то дискриминант будет полным квадратом. При этом а=-3 и х= 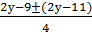. Отсюда х₁=0,5 и х₂=у-5. Уравнение принимает вид (2х-1)(х-у+5)=-3. (продолжи решение)

Метод решения относительно одной переменной

· Выделение целой части.

Задание 6 (МГУ, 1997). Найти все пары целых чисел х и у, удовлетворяющих уравнению 3ху+14х+17у+71=0

Решение: выразим из данного уравнения у через х: 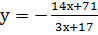. При этом следует отметить, что величина 3х+17 не равна нулю, так как х – целое число. Выделим из дроби в правой части этого равенства правильную Алгебраическую дробь (у которой степень числителя меньше степени знаменателя): . Умножим обе части последнего равенства на 3: или . Поскольку числа 3у и 14 – целые, то 3х+17 должно быть делителем числа 25, т.е. 3у+17= – всего 6 возможностей. Отсюда для х получаем три возможных значения: -4, -6, -14 (в остальных трех случаях х не является целым) Соответствующие значения у равны: -3, -13, -5.

Замечание: в данном примере суть выделения целой части состоит в избавлении переменной х из числителя. В решении был использован прием домножения обеих частей равенства на коэффициент при х в знаменателе. Этот прием домножения также удобно использовать при решении уравнений методом разложения на множители.

· Использование дискриминанта (неотрицательность).

Задание 7: Решить в целых числах уравнение 3(х 2 +ху+у 2 )=х+8у

Решение: Рассмотрим уравнение, как квадратное относительно х: 3(х 2 +ху+у 2 )-х-8у=0. Найдем дискриминант D=-27у 2 +90у+1. Данное уравнение имеет корни, если , т.е. -27у 2 +90у+1 . Т.к. то получаем, что . Перебирая эти значения, получаем решения уравнения.

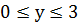
· Использование дискриминанта (полный квадрат).

Задание 7: Решить в целых числах уравнение х 2 -ху+у 2 =х+у

Решение: Рассмотрим уравнение как квадратное относительно х: х 2 –(у+1)х+у 2 -у=0. Его дискриминант D=-3у 2 +6у+1=t 2 должен быть квадратом некоторого целого числа t. Получаем новое уравнение: 3у 2 -6у-1+ t 2 =0; 3(у-1) 2 + t 2 =4. Из последнего уравнения следует, что t 2 4, .

1. Если t 2 =0, то уравнение 3(у-1) 2 =4 не имеет целого решения у.

2. Если t 2 =1, то уравнение 3(у-1) 2 =3 имеет целые решения у₁=2 и у₂=0. При у=2 получаем квадратное уравнение х 2 -3х+2=0 с корнями х=1 или х=2. При у=0 получаем квадратное уравнение х 2 -х=0 с корнями х=0 или х=1.

3. Если t 2 =4, то уравнение 3(у-1) 2 =0 имеет одно целое решение у=1. При у=1 получаем квадратное уравнение х 2 -2х=0 с корнями х=0 или х=2.

Метод оценки

· Использование известных неравенств.

Задание 8: Решить в натуральных числах уравнение

Решение: Пусть для определенности . Проведем перебор для первых значений неизвестной х.

1. Если х=1, то получаем неверное равенство 1+ , так как 1+ при любых натуральных у.

2. Если х=2, то получаем неверное равенство + , так как + при любых натуральных у.

3. Если х=3, то получаем + ; , у=6.

4. Если х=4, то получаем + ; , у=4.

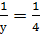
5. Если х=5, то получаем + ; , у= — не натуральное

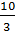
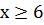
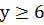
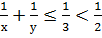
6. Пусть . По условию , следовательно, . Тогда , а значит, . Таким образом, при исходное уравнение решений не имеет.

Заметим, что в уравнении неизвестные х и у равноправны, поэтому снимая условие имеем еще одно решение (6;3). Кроме того, можно сделать вывод, что при исходное уравнение не имеет решений.

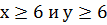
Задание 9: Решить в целых числах уравнение

Решение: Можно найти вначале решения только в натуральных числах, так как если (х₀; у₀; z₀) – решение, то, изменив знак у любых двух чисел этой тройки, снова получим решение. Данное уравнение умножим на 2xyz и воспользуемся неравенством ,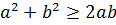

6xyz=2x 2 y 2 +2x 2 z 2 +2y 2 z 2 =(x 2 y 2 +x 2 z 2 )+(x 2 y 2 +y 2 z 2 )+(x 2 y 2 +y 2 z 2 ) 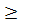2x 2 yz+2y 2 xz+2z 2 xy=2xyz(x+y+z), откуда x+y+z 3. Но х,у, z – натуральные, поэтому х=у= z=1 единственное решение в натуральных числах. Остальные решения в натуральных числах. Остальные решения исходного уравнения таковы: (-1; -1; 1); (1; -1; -1); (-1; 1; -1).

Ответ: (1; 1; 1); (-1; -1; 1); (1; -1; -1); (-1; 1; -1)

· Приведение к сумме неотрицательных выражений

Задание 10: Решить в целых числах уравнение х+у=х 2 -ху+у 2

Решение: приведем уравнение к виду (х-1) 2 +(у-1) 2 +(х-у) 2 =2. Так как (х-1) 2 2, то имеем (х-1) 2 =0 или (х-1) 2 =1. Отсюда получаем три значения х: 1, 0, 2. Подставляя эти значения в исходное уравнение, найдем значения у.

Решение нелинейных уравнений в целых числах

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

НАЦИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА «ИНТЕЛЛЕКТУАЛЬНО-ТВОРЧЕСКИЙ ПОТЕНЦИАЛ РОССИИ»
Секция : МАТЕМАТИКА
Методы решения нелинейных уравнений в целых числах
Ким Елена
МОУ лицей № 1, 10 класс, г. Комсомольск – на – Амуре
Научный руководитель:
Будлянская Наталья Леонидовна
Учитель математики высшей квалификационной категории
Решение нелинейных уравнений в целых числах

СОДЕРЖАНИЕ
Введение…………………………………………………………………………………слайд(ы) 3
Аннотация………………………………………………………………………………..слайд(ы) 4
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ:
1.Делимость целых чисел……………………………………………………………..слайд(ы) 5-6
2.Простые и составные числа………………………………………………………..слайд(ы) 7-8
3.НОК и НОД чисел……………………………………………………………………..слайд(ы) 9-13
4.Взаимно-простые числа……………………………………………………………..слайд(ы) 14
5.Линейные диофантовые уравнения……………………………………………….слайд(ы) 15-19
ПРАКТИЧЕСКАЯ ЧАСТЬ:
1.Разложение на множители………………………………………………………….слайд(ы) 20-21
2. Использование свойств простых чисел………………………………………. слайд(ы) 22-23
3.Выражение одной переменной через другую с последующим выделением целой части…………………………………………..…………. слайд(ы) 24-25
4.Использование свойств чётности и нечётности чисел…………………………слайд(ы) 26-27
5.Учёт ограниченности выражений………………………………………………….слайд(ы) 28
6.Учёт остатков от деления на число………………………………………………..слайд(ы) 29-30
7.Представление левой части уравнения в виде суммы неотрицательных слагаемых…………………………………………..слайд(ы) 31
8.Учёт свойств делимости……………………………………………………………..слайд(ы) 32
9.Введение новой переменной……………………………………………………. слайд(ы) 33
10.Другой метод решения уравнений ……………………………………………….слайд(ы) 34
Заключение………………………………………………………………………………слайд(ы) 35
Библиографический список……………………………………………………………слайд(ы) 36

ВВЕДЕНИЕ
Я ученица 9 класса физико-математической школы, лицея № 1, и вскоре, как и многие девятиклассники, буду проходить итоговую аттестацию. Тема для исследования «Методы решения нелинейных уравнений в целых числах» выбрана мною не случайно.
Во-первых, как в части В, так и в части С ГИА в 9-х классах есть задания, где можно будет применить знания методов решения нелинейных уравнений в целых числах. Во-вторых, умение качественно решать такие уравнения позволяют оценить мои математические навыки. Тем более умение решать уравнение различными способами высоко оценивается на олимпиадах регионального, всероссийского и международного уровней. В-третьих, передо мной была поставлена задача — провести исследования, результаты которых будут полезны и для учеников, и для учителей.
Свою работу я оформила в виде презентации, состоящей из двух частей: теоретической и практической. В теоретической части освещены базовые знания, которые необходимы при решении нелинейных уравнений в целых числах. В практической части я на примерах представила различные методы решения нелинейных уравнений, поэтому II часть моей работы относится к прикладным исследованиям.

АННОТАЦИЯ
Работа представлена в виде презентации, выполненной в программе Microsoft Office Power Point 2007. Она состоит из двух частей: теоретической и практической, — размещенных на 36 слайдах, включая титульный лист, оглавление, введение, аннотацию, заключение и библиографический список. В теоретической части мною освещены следующие темы: «Делимость целых чисел»,«Простые и составные числа», «НОК и НОД чисел», «Взаимно-простые числа», «Линейные диофантовые уравнения». В практической части рассматриваются различные методы решения нелинейных уравнений на примерах : «Разложение на множители», «Использование свойств простых чисел», «Выражение одной переменной через другую с последующим выделением целой части», «Использование свойств чётности и нечётности чисел», «Учёт ограниченности выражений», «Учёт остатков от деления на число», «Представление левой части уравнения в виде суммы неотрицательных слагаемых», «Учёт свойств делимости», «Введение новой переменной», «Другой метод решения уравнений».
Также к работе предоставлены тезисы, автореферат и данная аннотация.
Работа оформлена по правилам, представленным оргкомитетом конкурса «Первые шаги в науку».

ДЕЛИМОСТЬ ЦЕЛЫХ ЧИСЕЛ
ОПРЕДЕЛЕНИЕ : Если существует такое с, что а=b*с, то
а b (или b а). При этом с-частное от
деления а на b.
ОБОЗНАЧЕНИЕ: а b (а делится на b)

ПРОСТЕЙШИЕ СВОЙСТВА ДЕЛИМОСТИ
ЕСЛИ а N, b N,с N
1)а b, с-частное от деления с — единственное
2)а а, b b, с с…и.т.д.
3)а b, b c a c
4)a b, b а a=b a=-b
5)a b, b > a a=0
6)a b, a ≠ 0 a ≥ b
7)чтобы а b, необходимо и достаточно, чтобы а b

ДЕЛИМОСТЬ ЦЕЛЫХ ЧИСЕЛ
ПРОСТЕЙШИЕ СВОЙСТВА ДЕЛИМОСТИ :
ЕСЛИ а N, b N,с N
8) а1 b, a2 b… an b (a1±a2… ±an) b
9) (a1+a2+…+an) b и a1 b, a2 b…an-1 b an b
10)a b и a>0 a ≥ b
11)a b, b c, m N0, n N0, ma>nb, mo(ma-nb) c (ma+nb) c
12)a b, k ≠ 0 ak bk
13)ak bk, k ≠ 0 a b
14)a bc (a b) c
15)(a b) c a bc

ПРОСТЫЕ и СОСТАВНЫЕ ЧИСЛА
ОПРЕДЕЛЕНИЕ : Целое положительное число р>1
называется простым, если оно имеет ровно два
положительных делителя: 1 и р.
ОПРЕДЕЛЕНИЕ : Целое положительное число m>1
называется составным, если оно имеет, по крайней мере,
один положительный делитель, отличный от 1 и m.
СВОЙСТВА ПРОСТЫХ ЧИСЕЛ:
1)2 – единственное четное простое число
2)a и b – простые и a≠b a ≠ b*х
b ≠ a*у (х, у — некоторые числа)
3) а,b,c,d Z и аbcd е, причем е-простое а е или
b е или c е или d е
4)a Nо, а >1 наименьший положительный делитель
-простое число

ПРОСТЫЕ и СОСТАВНЫЕ ЧИСЛА
ОСНОВНАЯ ТЕОРЕМА АРИФМЕТКИ
a Nо, а ≠ 1, р1, р2, р3,……,рk – простые
а = р1*р2*р3*……*рk

Если среди чисел р1, р2, р3,……,рk есть одинаковые
а = р1 а1*р2 а2*р3 а3*……*рk аk

НОК и НОД чисел
ОПРЕДЕЛЕНИЕ:НОД чисел а1, а2…аn называется положительный
общий делитель, делящийся на любой другой
общий делитель этих чисел.
ОБОЗНАЧЕНИЕ: (a1, a2…an)=d, d-НОД чисел а1, а2…аn
a) d>0
b) d a1, d a2 … d an
Теорема 1:
1)Для любых чисел а1, а2…аn, из которых хотя бы одно отлично от нуля, существует НОД
2)p1,…,ps –различные простые числа a1=р1α1*…*рsαs,…,an=p1γ1*…*psγs
(а1, а2…аn)=p1min(α1,…,γ1) *…*psmin(α1,…,γs)
Замечание: способ нахождения НОД:
1)Разложить каждое число на простые множители, записав
разложение в каноническом виде
2)Найти произведение минимальных степеней простых множителей

НОК и НОД чисел
ПРИМЕР 1: Найти НОД чисел 10080, 2646, 56.
РЕШЕНИЕ:
1)10080 2 2646 2 56 2
5040 2 1323 3 28 2
2520 2 441 3 14 2
1260 2 147 3 7 7
630 2 49 7 1
315 3 7 7
105 3 1
35 5
7 7
1
2)d= 21*30*50*71= 2*7=14
(10080,2646,56)=14
10080=25*32*5*7 =25*32*51*71
2646=2*33*72 =21*33*50*72
56=23*7 =23*30*50*71

НОК и НОД чисел
Теорема 2: (a1, a2…an)=d, d b, b>0 ( ,…, )=
Теорема 3: (а1,…,an-1,an)=((a1,…,an-1),an)
n≥3 НОД n-чисел: 1)НОД (n-1)
2)НОД (d, an), d= (a1, a2…an), an -последнее число

ОПРЕДЕЛЕНИЕ: НОК чисел a1, a2,…,an называют
наименьшее положительное число,
делящееся на все эти числа.
ОБОЗНАЧЕНИЕ: [a1, a2…an]=m, m-НОК чисел a1, a2…an
а)m>0
b)a1 m,…,an m

НОК и НОД чисел
Теорема 5:
a1=р1α1*…*рsαs*,…,*an=p1γ1*…*psγs — каноническое разложение
m=[a1, a2…an]=p1max(α1,…,γ1) *…*psmax(α1,…,γs)
Теорема 6:
а>0, b>0, a N, b N, (a,b)=d, [a,b]=m
m=

Замечание: способ нахождения НОД:
1)Разложить число на простые множители,
записав разложение в каноническом виде
2)Найти произведение максимальных степе-
ней простых множителей, входящих в разложение

НОК и НОД чисел
ПРИМЕР 1: Найти НОК чисел 96,64,33,22.
РЕШЕНИЕ:
1)96 2 64 2 33 3 22 2
48 2 32 2 11 11 11 11
24 2 16 2 1 1
12 2 8 2
6 2 4 2
3 3 4 2
1 2 2

2)m=26*31*111=2112
[96,64,33,22]=2112
96=25*3 =25*31*110 64=26 =26*30*110 33=11*3=20*31*111 22=11*2=21*30*111

ВЗАИМНО-ПРОСТЫЕ ЧИСЛА
ОПРЕДЕЛЕНИЕ: а и b взаимно-простые числа, если (a,b)=1
Теорема 1: а Z, р Z, причем р — простое или а р
или а и р – взаимно-простые
Теорема 2: а,b – взаимно-простые [а,b]=ab
Теорема 3: Чтобы а:b или а:с достаточно и необходимо а: bс
Теорема 4: Если (а* b) с, причем (а,с)=1 b с

РЕШЕНИЕ ЛИНЕЙНЫХ ДИАФАНТОВЫХ УРАВНЕНИЙ
Общий вид диафантовых уравнений: ax+by=c
1.Найдем d(а, b)
2.Определим частное решение, выразив переменную х из данного уравнения, а переменную у находим, используя метод перебора (х0; у0)-частное решение.
3.Все остальные решения находим по формулам: х=-bk+x0, y=ak+y0, k Z

ПРИМЕР 1: Решить уравнение в целых числах х-3у=15
РЕШЕНИЕ:
a)НОД(1;3)=1
b)Определим частное решение: х=(15+3у):1
Используя метод перебора находим значения у=0, тогда
х=(15+0). Следовательно, (15;0) — частное решение
c)Остальные решения находим по формулам:
х=3k+15, k Z
y=k+0=k, k Z
ОТВЕТ: (3k+15; k), k Z

РЕШЕНИЕ ЛИНЕЙНЫХ ДИОФАНТОВЫХ УРАВНЕНИЙ

ПРИМЕР 2: Решить уравнение в целых числах 15х+11у=14
РЕШЕНИЕ:
а)НОД(15;11)=1
b)Определим частное решение: х=(14-11у):15
Используя метод перебора, находим значение у [0;14], т.к.
при остальных значениях (х;у), не входящих в этот
промежуток, выражение (14-11у):15 не будет являться
целым числом (противоречит условию).
(-2;4) – частное решение
c)Остальные решения находятся по формулам:
х=-11k-2, k Z
y=15k+4, k Z
ОТВЕТ: (-11k-2; 15k+4), k Z

РЕШЕНИЕ ЛИНЕЙНЫХ ДИОФАНТОВЫХ УРАВНЕНИЙ

ПРИМЕР 3: Купили 390 цветных карандашей в коробке по 7 и
12 карандашей. Сколько тех и других коробок купили?
РЕШЕНИЕ:
а)Пусть х – количество коробок по 7 карандашей, у — по 12.
Всего было куплено (7х+12у) карандашей, что по условию
задачи равно 390. Составим и решим уравнение.
7х+12у=390
b)НОД(7;12)=1
c)Определим частное решение: х=(390-12у):7 Используя метод перебора, находим значение у [1;6] (54;1) – частное решение
d)Остальные решения находим по формулам: х=-12k+54, y=7k+1 k Z

РЕШЕНИЕ ЛИНЕЙНЫХ ДИОФАНТОВЫХ УРАВНЕНИЙ

РЕШЕНИЕ ЛИНЕЙНЫХ ДИОФАНТОВЫХ УРАВНЕНИЙ

Уравнения, решаемые с помощью разложения на множители

Суть метода: сначала первоначальное уравнение путём группировки слагаемых и вынесения общих множителей приводится к виду, когда в левой части уравнения стоит произведение сомножителей, содержащих неизвестные, а справа стоит некоторое число.
ПРИМЕР 1: Решить в натуральных числах уравнение:
m2- n2=2001.
РЕШЕНИЕ: (m-n)(m+n)=2001
2001=3*23*29*1

ОТВЕТ: (1001;1000), (335; 332), (49; 20), (55;32)

ПРИМЕР 2: Решить в целых числах х2-3ху+2у2=3
РЕШЕНИЕ: Группировка: х2-2ху-ху+2у2=3; (х2-ху)-(2ху-2у2)=3
Вынесение общего множителя за скобки: х(х-у)-2у(х-у)=3;
(х-у)(х-2у)=3
Возможны 4 варианта:
1) 2) 3) 4)

(остальные 2 системы решаются подобным образом)
ОТВЕТ:(5:2); (1:2); (-5:-2); (-2:-1);
х-у=3
х-2у=1
х-у=-1
х-2у=-3
х-у=-3
х-2у=-1
х-у=1
х-2у=3
х=у+3
у+3-2у=1
х=5
у=2
х=1
у=2
х=у-1
у-1-2у=-3
Уравнения, решаемые с помощью разложения на множители

Использование свойств простых чисел
ПРИМЕР 1: Решить в натуральных целых числах 19х+89у=1989
РЕШЕНИЕ: 19х+89у=1989
19х-1900=89-89у
19(х-100)=89(1-у) (*)
(19;89) взаимно-простые равенство (*) возможно в 3 случаях
а) х-100=89 b) х-100=-89 c) х-100=0
1-у=19 1-у=-19 1-у=0

а) х = нет b) х=11 c) х=100
решений у=20 у=1
ОТВЕТ: (11;20), (100;1)

Использование свойств простых чисел
ПРИМЕР 2: Решить в простых числах х2-2у2=1
РЕШЕНИЕ: 2у2-четное х-нечетное
2у2=х2-1= (х-1)(х+1)
(х-1) : 2(т.к. четное)
(х+1): 2(т.к. четное)
у-четное
х,у-простые

ПРИМЕР 1: Решить уравнение в целых числах х2-ху+5х-9=0
РЕШЕНИЕ:

b) Z, если х= ±1, ±3, ±9

Уравнения, решаемые выражением одной переменной через другую с последующим выделением целой части
9
x
х2+5х-9
=
=
х+5
—
9
x
у Z
x

Уравнения, решаемые выражением одной переменной через другую с последующим выделением целой части
ПРИМЕР 2: Решить уравнение в целых числах у-х-ху=2
РЕШЕНИЕ:
а)Выразим у через х: (у-ху)=2+х
у(1-х)=2+х
у= =-1-
b)Т.к. х Z;у Z, то (х-1) может равняться ±1; ±3, откуда
х=2, у=-4,
х=0, у=2,
х=4, у=-2,
х=-2, у=0.
ОТВЕТ: (-2;0);(0;2);(2;-4);(4;-2)

Учет четности, нечетности чисел
ПРИМЕР 1: Доказать, что не существует целых решений уравнения х2+х+1 + у2+у+1 = 13
РЕШЕНИЕ:а)х2+х+1=х(х+1)+1
х(х+1)-четное
х2+х+1 — нечетное
b)аналогично у2+у+1 — нечетное
с) Противоречие: нечет.+нечет.=чет.
нечет.+нечет.=нечет.(по условию)

Учет четности, нечетности чисел
ПРИМЕР 2: Решить в целых числах уравнение х3+у3-3ху=2
РЕШЕНИЕ:
1)Если х, у нечетны х3-нечетное число
у3-нечетное число
3ху-нечетное число
Получаем: нечет+нечет-нечет ≠ чет
2)Если х-четное, у-нечетное х3-четное число
у3-нечетное число
3ху-четное число
Получаем: чет+нечет-чет ≠ чет
(аналогично, если х-нечетное, у-четное)
3)Если х-четное, у-четное, тогда пусть х=2m, y=2n
8m3+8n3-12mn=2 или 2(2m3+2n3-3mn)=1
невозможно ни при каких целых m и n
ОТВЕТ: решений нет

Учёт ограниченности выражений
ПРИМЕР 1: Решить уравнение в целых числах:
2(х4-2х2+3)(у4-3у2+4)=7 (1)
РЕШЕНИЕ: х4-2х2+3=х4-2х2+1+2=(х2-1)2+2≥2
у4-3у2+4=(у2-3 )2+7 ≥ 7
Л.Ч. ≥7, П.Ч.=7,значит, уравнение (1) равносильно системе :
(х2-1)2+2=2 х2-1 =0
(у2-3 ) +7 = 7 у2- =0

Откуда х =±1,у =± Z
ОТВЕТ: уравнение не имеет решений в целых числах.
(Возможен второй способ решения – использование свойств
простых чисел)
2
4
4
4
4
2
2

Учет остатков от деления на число
ПРИМЕР 1 : Решить в натуральных числах уравнение
n!+4n-9=k2
РЕШЕНИЕ: Заметим, что n!+4n-9=n!+4n-12+3
а)Если n ≥4, то (n!) 4, 4n 4, 12 4 (Ост4(n!+4n-9)=3)
В правой части уравнения стоит квадрат натурального числа k, который при делении на 4 не может давать в остатке 3. при n ≥4 уравнение не имеет корней.
b)Рассмотрим случаи, когда n=1,2,3 :
1.n=1 2.n=2 3.n=3
1+4-9=k2 2!+8-9=k2 3!+12-9=k2
-4=k2 1=k2 9=k2
k= k=1 k=3
ОТВЕТ: n=2, k=1
n=3,k=3

Учет остатков от деления на число
ПРИМЕР 2 : Решить в целых числах уравнение х2+1=3у
РЕШЕНИЕ:
а) 3у 3, при любом целом у
b) (х2+1)/3: (Ост3(х2+1)=0), (Ост3(х2+1)=1), (Ост3(х2+1)=2)
1.х=3k (Ост3(9k2+1)=1)
2.x=3k+1 (Ост3(9k2+6k+1+1)=2)
3.x=3k+2 (Ост3(9k2+12k+4+1)=2)
Получаем: ни при каких значениях х выражение (х2+1) не
делится на 3
при любом значении у выражение 3у кратно 3

Уравнение не имеет решений в целых числах
ОТВЕТ: решений нет

Уравнения, решаемые с помощью представления левой части уравнения в виде суммы неотрицательных слагаемых
ПРИМЕР 1: Решить уравнение в целых числах
5х4+10х2+2у6+4у3 =6
РЕШЕНИЕ:
5х4+10х2+2у6+4у3 = 5(х4 +2х2)+2(у6+2у3) = 5(х2+1)2+2(у3+1)2-7
Уравнения приводится к виду: 5(х2+1)2+2(у3+1)2=13

Отсюда имеем 5(х2+1)2 ≤13 так как (х2+1)2 – целое число, то (х2+1) может быть только равен 0,1,-1

Можно увидеть, что только х=0 возможен
5*1+2(у3+1)2=13 Тогда (у3+1)2=4 , у3+1=±2, но если у3+1=-2, то у=-3 ( не удовлетворяет условию) у3+1=2;у=1

Пример №1: Решить уравнение в целых числа
5х4+10х2+2у6+4у3 =6.
РЕШЕНИЕ:
5х4+10х2+2у6+4у3 = 5(х4 +2х2)+2(у6+2у3) = 5(х2+1)2+2(у3+1)2-7
Уравнения приводится к виду:
5(х2+1)2+2(у3+1)2=13
Отсюда имеем 5(х2+1)2 ≤13 так как (х2+1)2 – целое число, то (х2+1) может быть только равен 0,1,-1
Можно увидеть, что только х=0 возможен
5*1+2(у3+1)2=13 Тогда (у3+1)2=4 , у3+1=±2, но если у3+1=-2, то у=-3 ( не удовлетворяет условию) у3+1=2;у=1

Учет свойств делимости
ПРИМЕР 1 : Решить в целых числах уравнение х3-100=225у
РЕШЕНИЕ: Очевидно, что х3 должен быть кратен 5
Пусть х= 5z, z Z, тогда 125z3-100=225y
5z3-4=9y (1)
Очевидно,что левая часть уравнения должна быть кратна 9,т.е
a) z=3t b) z=3t+1 c) z=3t-1
5(3t)3-4=9y 5(3t+1)3-4=9y 5(3t-1)3-4=9y
135t3-4=9y 5(27t3+27t2+9t+1)-4=9 5(27t3-27t2+9t-1)-4=9y
135t3+135t2+45t+1=9y 135t3-135t2+45t-9=9y
т.е. z=3t-1, тогда х=15t-5, y=15t3-15t2+5t-1
ОТВЕТ: (15t-5; 15t3-15t2+5t-1), t Z

Уравнения, решаемые с помощью введения новой переменной
ПРИМЕР 1: Решить уравнение в целых числах: 7(х+у)=3(х2-ху+у2)
РЕШЕНИЕ: Пусть х+у=р, х-у=q. Тогда, выразив х и у, получим: х= p+q , у=p-q . Подставим в исходное уравнение: 7р= — — 7р= т.к.28p=3(p2+3q), то p–неотрицательное и p 3, т.е p=3k, k Z Подставив p=3k, получим 28*3k=3((3k)2 +3q2); 28k=3(3k2 +q2). Отсюда следует, что k 3, поэтому k=3m, m Z; Подставив k=3m, получим 28*3m=3(3(3m)2 + q2;
28m=27m2+q2 ;
m(28-27m)=q2; так как q2≥0, то m=0, или m=1 (решаем неравенство m(28-27m) ≥0 c помощью метода интервалов)
а)Если m=0, k=0 (т.к. k=3m), p=0 (т.к. p=3k), q=0(т.к. 28p=3(p2+3q)), значит, х=0, у=0 (т.к. x=p+q , у= p-q
b)Если m=1, k=3, p=9, q2=1(т.к. m(28-27m)=q2)
а)q= 1, получаем х=5; у=4; b) q= -1, получаем х=4; у=5;
ОТВЕТ:(5:4);(4:5);(0:0)
Второй способ решения – использование свойств взаимно — простых чисел

Другие методы решения уравнений
ПРИМЕР 1 : Решить уравнение в целых числах 10х+у=х2+у2+13
РЕШЕНИЕ:
10х+у=х2+у2-13
х2-10х+у2-у+13=0
D/4=25-y2+y-13
Уравнение имеет корни при D/4≥0, т.е.
25-у2+у-13 ≥0
-у2+у+12 ≥0 *(-1)
у2-у-12≤0
D=1-4*(-12)=49=72
y1=-3
y2=4
+ +
-3 — 4 У
т.е. -3 ≤у ≤4, т.о. переберем все возможные случаи:
у=4, 3, 2, 1,0,-1,-2,-3
ОТВЕТ: (-5;-3), (5;4)

ЗАКЛЮЧЕНИЕ
Мною была проведена научно — исследовательская работа в разделе математики по изучению различных методов решения нелинейных уравнений в целых числах.
Моей целью было качественно изучить методы решения таких уравнений и представить результаты другим ученикам.
Работа велась в течение нескольких месяцев. За это время я прочитала немало научной литературы, изучила многие методы решения нелинейных уравнений в целых числах, а также приобрела опыт в ведении научно – исследовательской работы. За это время я убедилась в актуальности темы, выбранной мною, т.к. моя работа была представлена всем ученикам старших классов, особенно 9 и 11. В большей степени учащихся интересовала практическая часть работы, ведь на примере всегда проще рассмотреть, тем более, что теоретическую часть знало большинство из них.
Несмотря на то, что работа велась самостоятельно, неоценимую помощь как в предоставлении научных материалов, так и в информационной поддержке, оказал мне мой научный руководитель, Наталья Леонидовна Будлянская.
В завершение хочу сказать, что те цели, которые были поставлены передо мной, на мой взгляд, я выполнила.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК
— Балк М.Б., Балк Г.Д.. Математика после уроков. Москва, издательство «Просвещение», 1971, — 462 с..
— Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И.. Задачи по математике. Уравнения и неравенства. Справочное пособие. Москва, издательство «Наука», 1960, — 608 с..
— Власов А.П., Евсеев Н.В.. Полный комплект пособий для подготовки к ЕГЭ. «50 типовых экзаменационных работ». Москва, издательство АСТ «Астрель», 2009, — 320 с..
— Гельфонд А.О.. Решение уравнений в целых числах. Москва, издательство «Наука», 1978, — 63 с..
— Горбачев Н.В.. Сборник олимпиадных задач по математике. Москва, издательство МЦНМО, 2004, — 560 с..
— Кушнир И.. Шедевры школьной математики. Киев, издательство «Астарта», 1995, — 576 с..
— Шарыгин И.Ф.. Решение задач. Москва, издательство «Просвещение», 1994, — 252 с..

Нелинейные диофантовы уравнения Методическая разработка учителя Поляковой Е. А. — презентация

Презентация была опубликована 6 лет назад пользователемКирилл Ашанин

Похожие презентации

Презентация на тему: » Нелинейные диофантовы уравнения Методическая разработка учителя Поляковой Е. А.» — Транскрипт:

1 Нелинейные диофантовы уравнения Методическая разработка учителя Поляковой Е. А.

2 Решение уравнений в целых или в натуральных числах одна из наиболее древних задач математической науки, важная и для современной математики. Существенной особенностью таких уравнений является наличие в одном уравнении нескольких переменных. Задача состоит в следующем: для заданного уравнения надо найти все целые или натуральные значения переменных, входящих в уравнение, при которых оно превращается в истинное равенство.

3 В истории математики задача решения уравнений в натуральных числах связывается с именем древнегреческого математика Диофанта, придумавшего для таких уравнений много разнообразных приёмов решения, и поэтому их называют диофантовыми. Так же называют и уравнения в целых числах. Ввиду бесконечного разнообразия диофантовых уравнений общего алгоритма их решений не существует, и практически для каждого уравнения приходится изобретать индивидуальный приём.

4 Простейший приём их решения перебор, который всегда пытаются сократить с помощью дополнительных соображений. Решение. Так как обе переменные входят в уравнение в чётных степенях, то достаточно найти только натуральные решения, а затем в полученных решениях произвольным образом поставить знаки. Пример 1. Решить уравнение 2 x² + y² = 267 в целых числах. Вначале ограничим объём перебора заметим, что 2 х²

5 х² х²2 х² у²у² у 135 Из этой таблицы видно, что данное уравнение имеет решения (±7, ±13) и (±11, ±5), или подробнее : (7, 13), (7, 13), (7, 13), (7, 13), (11, 5), (11, 5), (11, 5), (11, 5).

6 Можно было бы заметить, что в любом решении данного уравнения число у должно быть нечётным, т. е. у = 2z 1, и переписать уравнение в виде 2 х² + (2z 1)² = 267, 2x² + (4z² 4z + 1) = 267, x² + 2z² 2z = 133. Из последнего равенства следует, что число х также нечётное, и теперь понадобится перебор всего 6, а не 11 значений х, как в приведённом решении.

7 Ответ:(1 + 2 n; 23n), nцелое число. Пример 2. Решить уравнение 2x ³ + 3y² = 397 в целых числах. Решение. Вначале ограничим объём перебора заметим, что 3 у²

8 Очевидно, что в уравнении одно решение: (5;7). у² у²3 у² х³2 х³ х³х³ х 5

9 Решение. Заметим, что 1 = 1 1 = 1 (1). Значит, возможны варианты: Рассмотрим другие способы решения нелинейных диофантовых уравнений. Пример 3. Решить уравнение (х 2)(х у + 4) = 1 в целых числах. 1) х 2 = 1, тогда х = 3, значит 3 у + 4 = 1, у = 1; 2) х 2 = 1, тогда х = 1, значит у + 4 = 1, у = 5. Ответ: (3; 1); (1; 5).

10 Пример 4. Решить уравнение 2 х² + х у = х + 7 в целых числах. Решение. Перепишем заданное уравнение в виде 2 х² + х у х = 7, х (2 х + у 1) = 7. Заметим, что 7 = 1 7 = 1 (7) = 7 1 = 7 (1) Значит, возможны варианты: 1) х = 1, у 1 = 7, у = 6; 3) х = 7, 14 + у = 1, у = 12. 2) х = 1, 2 + у 1 = 7, у = 4. 4) х = 7, 14 + у 1 = 1, у = 14. Ответ: (1; 6); (1; 4), (7; 12), (7; 14).

11 Пример 5. Решить уравнение х² х у х + у = 1 в целых числах. Решение. Перепишем заданное уравнение в виде х ( х у ) ( х у ) = 1, (х у )( х 1) = 1. Заметим, что 1 = 1 1 = 1 (1). Значит, возможны варианты: 1) х 1 = 1, тогда х = 2, значит 2 у = 1, у = 1; 2) х 1 = 1, тогда х = 0, значит 0 у = 1, у = 1. Ответ: (2; 1); (0; 1).

12 Пример 6. Решить уравнение х² 3 х у = х 3 у + 2 в целых числах. Решение. Перепишем заданное уравнение в виде х 3 ху х + 3 у = 2, х ( х 1 ) 3 у( х 1 ) = 2, (х 1)( х 3 у) = 2. Заметим, что 2 = 1 2 = 2 1 = 1 (2) = 2 (1). 1) х 1 = 1, тогда х = 2, у = 0; 3) х 1 = 1, тогда х = 0, у = 2/3; Ответ: (2; 0); (1; 0). 2) х 1 = 2, тогда х = 3, у = 2/3; 3) х 1 = 2, тогда х = 1, у = 0.

13 Пример 7. Решить уравнение у² 2 х у = 2 х + 6 в целых числах. Ответ: (0; 0); (3; 1). Ответ: (1; 4); (3; 6), (1; 2), (3; 0). Пример 8. Решить уравнение 3 у + 3 х у + 2 х = 0 в целых числах. Пример 9. Решить уравнение у + 2 х у + 4 х = 0 в целых числах. Ответ: (0; 0); (1; 4).

14 Ответ: (0; 0); (2; 2). Ответ: (0; 2); (4; 2), (2; 4), (2; 0). Пример 12. Решить уравнение 2 у² 3 х у + х² = 3 в целых числах. Пример 10. Решить уравнение у + х = х у в целых числах. Пример 11. Решить уравнение у х = х у + 2 в целых числах. Ответ: (5; 2); (1; 2), (5; 2), (1; 2). Задания для самостоятельного решения