Решение нелинейных уравнений
Уравнения, в которых содержатся неизвестные функции, произведенные в степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение, х^3 – 0,2x^2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).
Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.
Существует множество методов решения нелинейных уравнений и систем нелинейных уравнений, которые принято относить в 3 группы: численные, графические и аналитические. Аналитические методы позволяют определить точные значения решения уравнений. Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений. Численное решение нелинейных уравнений предполагает прохождения двух этапов: отделение корня и его уточнение до определенно заданной точности.
Отделение корней осуществляется различными способами: графически, при помощи различных специализированных компьютерных программ и др.
Рассмотрим несколько методов уточнения корней с определенно заданной точностью.
Методы численного решения нелинейных уравнений
Метод половинного деления.
Суть метода половинного деления заключается в делении интервала [a,b] пополам (с=(a+b)/2) и отбрасывании той части интервала, в которой отсутствует корень, т.е. условие F(a)xF(b)
Рис.1. Использование метода половинного деления при решении нелинейных уравнений.
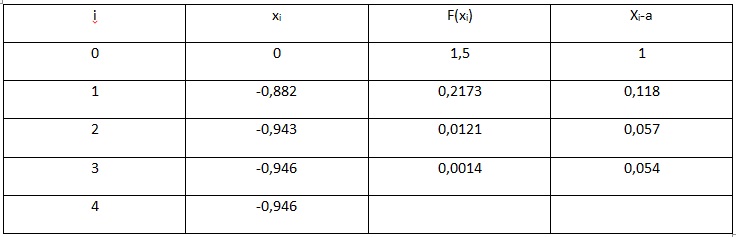
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0, то начала отрезка a переносится в x (a=x), иначе, конец отрезка b переносится в точку x (b=x). Полученный отрезок делим опять пополам и т.д. Весь произведенный расчет отражен ниже в таблице.
Рис.2. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
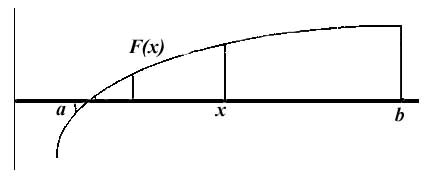
При использовании метода хорд, задается отрезок [a,b], в котором есть только один корень с установленной точностью e. Через точки в отрезке a и b, которые имеют координаты (x(F(a);y(F(b)), проводится линия (хорда). Далее определяются точки пересечения этой линии с осью абсцисс (точка z).
Если F(a)xF(z)
Рис.3. Использование метода хорд при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0;
Определим вторую производную F’’(x) = 6x-0,4.
F’’(-1)=-6,4 0 соблюдается, поэтому для определения корня уравнения воспользуемся формулой:
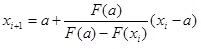
, где x0=b, F(a)=F(-1)=-0,2
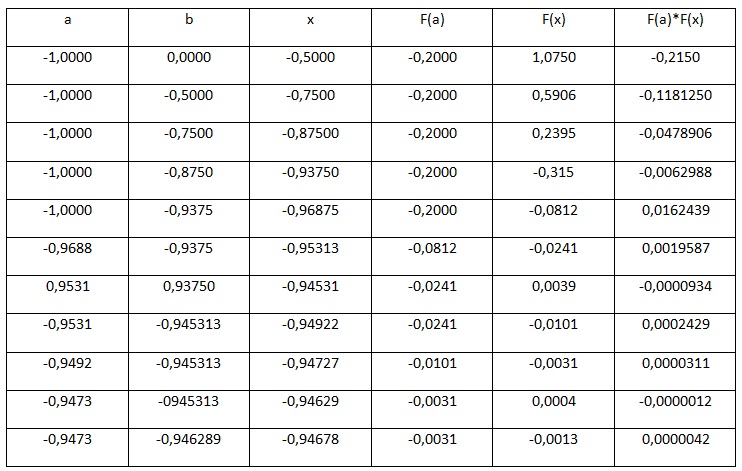
Весь произведенный расчет отражен ниже в таблице.
Рис.4. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
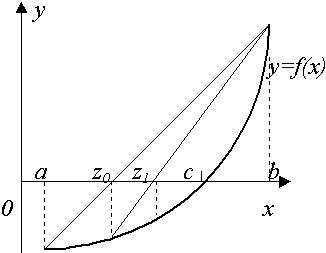
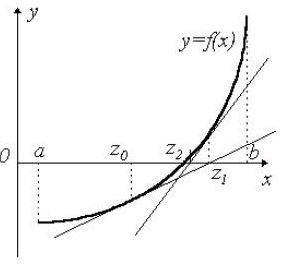
Метод касательных (Ньютона)
Данный метод основывается на построении касательных к графику, которые проводятся на одном из концов интервала [a,b]. В точке пересечения с осью X (z1) строится новая касательная. Данная процедура продолжается до тех пор, пока полученное значение не будет сравним с нужным параметром точности e (F(zi)
Рис.5. Использование метода касательных (Ньютона) при решении нелинейных уравнений.
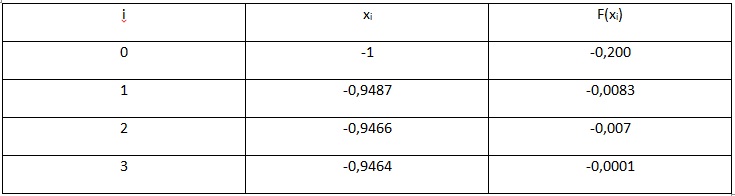
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0 выполняется, поэтому расчеты производим по формуле:
Весь произведенный расчет отражен ниже в таблице.
Рис.6. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
НЕЛИНЕ́ЙНОЕ УРАВНЕ́НИЕ
В книжной версии
Том 22. Москва, 2013, стр. 345-346
Скопировать библиографическую ссылку:
НЕЛИНЕ́ЙНОЕ УРАВНЕ́НИЕ, алгебраическое или трансцендентное уравнение вида $$f(x)=0,\tag1$$ где $x$ – действительное число, $f(x)$ – нелинейная функция. Системой Н. у. называется система $$\begin
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №43.Нелинейные уравнения и неравенства с двумя переменными.
Перечень вопросов, рассматриваемых в теме:
- уравнение и неравенство, способы их решения;
- система уравнений, система неравенств;
- изображение в координатной плоскости множество решений уравнений, неравенств, систем уравнений, систем неравенств и нахождение площади получившейся фигуры;
Глоссарий по теме
Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.
Все уравнения, которые не являются линейными называются нелинейными.
Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с 0, где х и у – переменные, а, b, c – некоторые числа.
Все неравенства, которые не являются линейными называются нелинейными.
Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Все системы неравенств, которые не являются линейными называются нелинейными.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Учебник: Алгебра 9 кл с углубленным изучением математики Мнемозина, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Сегодня на уроке мы вспомним нелинейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое нелинейным уравнением и неравенством.
1.Линейные уравнения с двумя переменными.
Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.
Все уравнения, которые не являются линейными называются нелинейными.
Например, 
Нелинейные уравнения с двумя переменными изображаются на координатной плоскости различными фигурами, каждое уравнение нужно рассматривать индивидуально.
Найти множество точек координатной плоскости, удовлетворяющих уравнению:
Уравнение запишем в виде (х-у)(х+у) = 0, значит либо х-у=0, либо х
+у=0. Поэтому множество точек удовлетворяющих уравнению – пара пересекающихся прямых.
Преобразуем левую часть уравнения, используя метод выделения полного квадрата:
Сумма неотрицательных слагаемых равна 0 только в одном случае, когда оба слагаемых одновременно равны 0.
Это уравнение имеет единственное решение: х=2; у=-3. Поэтому множество точек удовлетворяющих уравнению – точка (2;-3).
Пусть на координатной плоскости Оху выбрана точка А(а;b), М(х;у) – произвольная точка этой плоскости, R- расстояние от точки М до точки А. Тогда 
Запишем уравнение в виде 
Рассмотрим примеры уравнений с двумя переменными, содержащих знак модуля:
Если 
Аналогично строятся отрезки в трех оставшихся координатных углах. (рисунок 1)
Рисунок 1 – графика
2.Нелинейные неравенства с двумя переменными.
Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с 0, где х и у – переменные, а, b, c – некоторые числа.
Все неравенства, которые не являются линейными называются нелинейными.
Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное равенство.
Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.
- Некоторые из таких неравенств можно привести к виду у f(x), а нижняя – графиком неравенства у 0 удовлетворяют все те точки, которые находятся от точки А на расстоянии меньшем R, те все точки и только они, расположенные внутри окружности с радиусом R и центром в точке А(а;b). Аналогично, множество решений неравенства
есть множество точек , лежащих вне окружности.
Изобразите в координатной плоскости множества решений неравенства 
- Начертим график уравнения
. Запишем уравнение в виде
Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка.
- Искомое множество решения неравенства – множество точек, лежащих на окружности и внутри окружности с центром в точке (-1;4) и радиусом 3 единичных отрезка.
3. Системы нелинейных уравнений с двумя переменными.
Система вида 
Все системы уравнений, которые не являются линейными называются нелинейными.
Пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство называют решением системы.
Решить систему – значит найти множество ее решений.
Каждое решение уравнения с двумя переменными представляет координаты некоторой его точки его графика. Каждое решение системы есть координаты общих точек графиков уравнений системы. Построим графики этих уравнений и найдем координаты точек пересечения.
Например.
Решить систему уравнений
Первое уравнение системы задает параболу, второе – окружность с центром (-1;3) и радиусом 
Рисунок 2 – решение системы
4. Системы нелинейных неравенств с двумя переменными.
Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Все системы неравенств, которые не являются линейными называются нелинейными.
Рассмотрим систему нелинейных неравенств с двумя переменными на примере:
Изобразить на координатной плоскости Оху фигуру Ф, заданную системой неравенств, и найти площадь фигуры:
Неравенство 




Рисунок 3 – решение системы
- Найти множество точек координатной плоскости, удовлетворяющих уравнению
.(рисунок 4)
График уравнения х^2 

Рисунок 4 – график уравнения
Заметим, что фигуру, которая получается сжатием окружности к одному из ее диаметров, называют эллипсом.
- Уравнение вида
— уравнение ромба , где точка (a;b) точка пересечения диагоналей; диагонали ромба соответственно равны
.
Рассмотрим частный случай:
Если k=m, то диагонали ромба будут равны, значит заданная фигура – квадрат.
Примеры и разборы решений заданий тренировочного модуля
Графиком данного уравнения является парабола, показанная на рисунке.(рисунок 5)
Рисунок 5 – график
Изобразите в координатной плоскости множества решений неравенства 
Начертим график уравнения 
Проверим себя: Например, пара (0;0) является решением неравенства 
http://bigenc.ru/mathematics/text/2258043
http://resh.edu.ru/subject/lesson/6123/conspect/
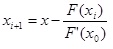














 есть множество точек , лежащих вне окружности.
есть множество точек , лежащих вне окружности. . Запишем уравнение в виде
. Запишем уравнение в виде  Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка.
Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка.




 .(рисунок 4)
.(рисунок 4)

 — уравнение ромба , где точка (a;b) точка пересечения диагоналей; диагонали ромба соответственно равны
— уравнение ромба , где точка (a;b) точка пересечения диагоналей; диагонали ромба соответственно равны  .
.


