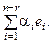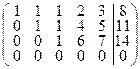Неоднородная система линейных уравнений может быть несовместимой

Неоднородные системы

Рассматривается неоднородная система линейных уравнений Ах = b с n-неизвест-ными.

12°. (Кронекер-Капелли). Система Ах = b совместна тогда, и только тогда, когда ранг главной матрицы системы совпадает с рангом расширенной матрицы rangA =rangà (à = (A|b)).

◀ 1) Пусть система Ах = b – совместна Þ $с такой, что Ас = b т.е. c₁S₁ + c₂S₂ +…+ c_nS_n=b. Таким образом, последний столбец матрицы à является линейной комбинацией столбцов матрицы А Þ rangA = rangà .

13°. Если неоднородная система линейных уравнений совместна и rangA = rangà = n,то она имеет единственное решение (по теореме Крамера).

Пусть теперь rangA = rangà = r ≤ n.

14°. Разность двух различных решений неоднородной системы линейных уравнений является решением соответствующей однородной системы, т.е. если c (2) и c (1) два решения неоднородной системы Ах = b, то c (2) – c (1) решением однородной системы Ах = 0.

◀ А(c (2) – c (1) ) = Аc (2) – Аc (1) = b – b = 0,т.е. c (2) – c (1) = c (0) . Здесь через c (0) обозначено некоторое решение однородной системы. ▶

15°. Сумма любого решения однородной системы c (0) и некоторого решения неоднородной системы c (1) есть решение неоднородной системы.

Предыдущие два утверждения доказывают теорему об общем виде решения неоднородной системы и линейных уравнений.

16°. Общее решение неоднородной системы уравнений есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Эту фразу можно записать с помощью легко запоминающейся аббревиатуры:

О. Р. Н. С. = О. Р. О. С. + Ч. Р. Н. С.

Способ решения неоднородных систем линейных уравнений таков:

1). Если rangA = rangà = n, то решение единственно и может быть найдено по Крамеру;

2). ЕслиrangA = rangà = r (неодн.) = x (частн.) +

Система векторов <e₁, e₂, . e_n–r> называется фундаментальной системой решений для системы уравнений Ах = 0.

Если М – множество решений неоднородной системы уравнений, x (r) – некоторое частное решение неоднородной системы уравнений, L– пространство решений соответствующей линейной однородной системы, то M = x (r) + L, т.е. М – есть линейное многообразие размерности n – r.

§8. Метод Гаусса РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. (метод исключения неизвестных)

Решить систему уравнений: .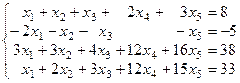

Записав расширенную матрицу системы, преобразуем ее с помощью преобразований не изменяющих ранг матрицы. Цель: в первом столбце все элементы, кроме одного, должны стать равными нулю. Это равносильно тому, что из 2 го , 3 го и 4 го уравнений будет исключена неизвестная х₁. Для достижения цели первую строку, умноженную на 2, –3 и –1 прибавим, соответственно, к 2 ой , 3 ей и 4 ой строке. Получим:

.

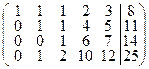
Примечание: здесь и в дальнейшем знак

, стоящий между двумя матрицами означает, что справа и слева от этого знака стоят матрицы одинакового ранга и, следовательно, системы линейных уравнений с такими матрицами имеют одинаковые решения.

Далее вторую строку, умноженную на –1 прибавим к 4 ой строке, тем самым исключив х₂ из третьего и четвертого уравнений и, наконец исключим х₃ из 4 го уравнения, прибавив третью строку, умноженную на –1 к четвертой:

.

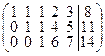
Имеем rangA = rangà = 3. Система совместна. n – r =5 –3 = 2, dimL =dimM =2. Так как, размерность пространства решений однородной системы равна 2, то в системе имеется две свободных неизвестных. Выберем в качестве свободных переменных х₃, х₄. Отделим в матрице свободные неизвестные вертикальной пунктирной линией: .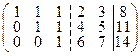

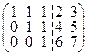
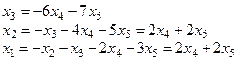
Далее рассмотрим однородную систему уравнений с матрицей . Тогда

.

Если положить х₄ = х₅ = 0, то получим х₃ = 14, х₂ = –3, х₁ = –3, т.е. (–3, –3, 14, 0, 0) еще одно частное решение данной системы. Следовательно, общее решение исходной системы можно записать и в таком виде: х = (–3, –3, 14, 0, 0) + a(2, 2, –6, 1, 0) + b(2, 2, –7, 0, 1), где a, b – любые.

Нужно обратить внимание и на то, что разность двух частных решений неоднородной системы (–3, –3, 14, 0, 0) – (1, 1, 1, 1, 1) есть решение соответствующей однородной системы уравнений.

§9. «Альтернатива Фредгольма»

Для квадратной системы (j =1, 2, …, п):

а) или система имеет решение, притом единственное при любых b_j, если соответствую­щая однородная система имеет только тривиальное решение (detA ≠0),

б) или соответствующая однородная система имеет ненулевые решения (detA = 0) и, следовательно, есть такие b_j, при которых система не имеет решений.

Неоднородная система линейных уравнений может быть несовместимой

Пусть задана неоднородная система линейных алгебраических уравнений размерности m × n .

Матрица называется расширенной матрицей системы, если наряду с коэффициентами при неизвестных, она содержит столбец свободных членов. Следовательно, размерность равна m × (n+1) .

Исследование любой системы линейных алгебраических уравнений начинается с преобразования ее расширенной матрицы методом Гаусса , который основан на следующих элементарных преобразованиях:

– перестановка строк матрицы;

– умножение строк матрицы на действительное отличное от руля число;

– поэлементное сложение строк матрицы;

– вычеркивание нулевой строки;

– транспонирование матрицы (в этом случае преобразования производятся по столбцам).

Элементарные преобразования приводят первоначальную систему к системе, ей эквивалентной. Системы называются эквивалентными, если они имеют одно и то же множество решений.

Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Элементарные преобразования ранга матрицы не меняют.

На вопрос о наличии решений у неоднородной системы линейных уравнений отвечает следующая теорема.

Теорема 1.3 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу ее главной матрицы, то есть

Обозначим количество строк, оставшихся в матрице после метода Гаусса, через r (соответственно, в системе остается r уравнений). Эти строки матрицы называются базисными.

Если r = n , то система имеет единственное решение (является совместной определенной), ее матрица элементарными преобразованиями приводится к треугольному виду. Такую систему можно решить также методом Крамера и с помощью обратной матрицы .

Если r n (количество переменных в системе больше количеств а уравнений), матрица элементарными преобразованиями приводится к ступенчатому виду. Такая система имеет множество решений и является совместной неопределенной. В данном случае для нахождения решений системы необходимо выполнить ряд операций.

1. Оставить в левых частях уравнений системы r неизвестных (базисные переменные), остальные n — r неизвестных перенести в правые части (свободные переменные). После разделения переменных на базисные и свободные система принимает вид:

2. Из коэффициентов при базисных переменных составить минор (базисный минор), который должен быть отличен от нуля.

3. Если базисный минор системы (1.10) равен нулю, то одну из базисных переменных следует заменить на свободную; полученный базисный минор снова проверить на отличие от нуля.

4. Применяя формулы (1.6) метода Крамера, считая правые части уравнений их свободными членами, найти выражение базисных переменных через свободные в общем виде. Полученный при этом упорядоченный набор переменных системы является ее общим решением.

5. Придавая свободным переменным в (1.10) произвольные значения, вычислить соответствующие значения базисных переменных. Получаемый при этом упорядоченный набор значений всех переменных называется частным решением системы, соответствующим данным значениям свободных переменных. Система имеет бесконечное множество частных решений.

6. Получить базисное решение системы – частное решение, получаемое при нулевых значениях свободных переменных.

Заметим, что количество базисных наборов переменных системы (1.10) равно числу сочетаний из n элементов по r элементов C_n r . Так как каждому базисному набору переменных соответствует свое базисное решение, следовательно, количество базисных решений у системы также равно C_n r .

Пусть строки матрицы обозначены соответственно l ₁ ; l ₂ ;…; l_n . Строка l называется линейной комбинацией строк l ₁ ; l ₂ ;…; l_n матрицы, если она равна сумме произведений этих строк на произвольные действительные числа, то есть , .

Однородная система уравнений всегда совместна, так как имеет хотя бы одно – нулевое (тривиальное) решение. Для того чтобы однородная система n линейных уравнений с n переменными имела ненулевые решения, необходимо и достаточно, чтобы ее главный определитель ∆ был равен нулю. Это означает, что ранг r ее главной матрицы меньше числа n неизвестных ( r n ) . В этом случае исследование однородной системы уравнений на общее и частные решения проводится аналогично исследованию неоднородной системы. Решения однородной системы уравнений обладают важным свойством: если известны два различных решения однородной системы линейных алгебраических уравнений, то их линейная комбинация также является решением этой системы. Нетрудно убедиться в справедливости следующей теоремы.

Теорема 1.4. Общее решение неоднородной системы уравнений представляет собой сумму общего решения соответствующей однородной системы и некоторого частного решения неоднородной системы уравнений

Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение:

Решение. Выпишем расширенную матрицу системы и применим к ней элементарные преобразования:

Так как r ( A ) =2 и , то по теореме 1.3 (Кронекера-Капелли) заданная система линейных алгебраических уравнений совместна. Количество переменных n =2 , т.е. r n , значит, система является неопределённой. Количество базисных наборов переменных системы равно . Следовательно, базисными могут быть 6 комплектов переменных: < x ₁ ; x ₂ >, < x ₁ ; x ₃ >, < x ₁ ; x ₄ >, < x ₂ ; x ₃ >, < x ₂ ; x ₄ >, < x ₃ ; x ₄ > . Рассмотрим один из них < x ₁ ; x ₂ > . Тогда систему, полученную в результате метода Гаусса, можно переписать в виде . Главный определитель . С помощью метода Крамера ищем общее решение системы.

По формулам (1.6) имеем

Данное выражение базисных переменных через свободные представляет собой общее решение системы:

При конкретных значениях свободных переменных из общего решения получаем частное решение системы. Например, частное решение соответствует значениям свободных переменных x ₃ = x ₄ = 17 . При x₃=0 x₄=0 получаем базисное решение системы

Неоднородная система линейных уравнений может быть несовместимой

линейных уравнений называется совместной, если у неё есть хотя бы одно решение, и несовместной, если решений нет. В примере 14 система совместна, столбик является её решением:

Это решение можно записать и без матриц: x = 2, у = 1.

Систему уравнений будем называть неопределённой, если она имеет более одного решения, и определённой, если решение единственно.

Пример 15. Система является неопределённой. Например, . являются её решениями. Читатель может найти и много других решений этой системы.

Научимся решать системы линейных уравнений сначала в частном случае. Систему уравнений AX = B будем называть крамеровской, если её основная матрица А — квадратная и невырожденная. Другими словами, в крамеровской системе число неизвестных совпадает с числом уравнений и |A| = 0.

Теорема 6 (правило Крамера). Крамеровская система линейных уравнений имеет единственное решение, задаваемое формулами:

где Δ = |A| — определитель основной матрицы, Δi — определитель, полученный из A заменой i-го столбика столбиком свободных членов.

Доказательство проведём для n = 3, так как в общем случае рассуждения аналогичны.

Итак, имеется крамеровская система:

Допустим сначала, что решение системы существует, т. е. имеются

Умножим первое . равенство на алгебраическое дополнение к элементу aii, второе равенство — на A2i, третье — на A3i и сложим полученные равенства: