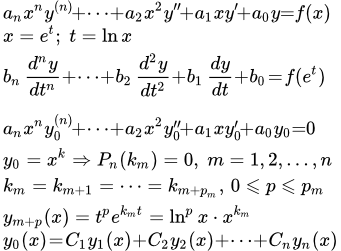Неоднородное уравнение эйлера со специальной неоднородной частью

Дифференциальное уравнение Эйлера и методы его решения

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

Уравнение Эйлера

Уравнением Эйлера называется линейное дифференциальное уравнение с переменными коэффициентами вида

Такой специальный вид линейного дифференциального уравнения позволяет свести это линейное уравнение с переменными коэффициентами к линейному уравнению с постоянными коэффициентами заменой независимого переменного для и для .

Действительно, при такой замене получаем: , и уравнение с переменными коэффициентами становится уравнением с постоянными коэффициентами. Для уравнения с постоянными коэффициентами будет иметь следующий вид:

Решить уравнение Эйлера:.

Составим характеристическое уравнение: . Его корни . Следовательно, общее решение однородного уравнения с постоянными коэффициентами такое: .

Решаем неоднородное уравнение. Составляем его, используя характеристическое уравнение: Частное решение ищем в виде . Подставляем в уравнение:. Итак, решение исходного уравнения

Чтобы решить однородное уравнение можно поступить проще: искать решения в виде одночлена . Приведем пример:

Решить однородное уравнение Эйлера: . Подставим в уравнение: . Корни уравнения . Поэтому частными решениями будут: , а общим решением исходного уравнения будет: .

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Задача Коши и Уравнение Эйлера

Как известно, задача Коши для линейного неоднородного уравнения состоит в следующем: найти решение этого уравнения, удовлетворяющее начальным условиям (данным Коши)

Пример 11. Найти частное решение уравнения

удовлетворяющее начальным условиям

Решение. Находим частное решение уравнения

Для решения поставленной начальной задачи Коши требуется определить значения постоянных и так, чтобы решение (24) удовлетворяло начальным условиям (23). Используя условие , получаем . Дифференцируя (24), найдем

откуда, в силу условия , будем иметь . Для отыскания получили систему

решая которую находим . Подставляя найденные значения произвольных постоянных в общее решение (24), получаем решение исходной задачи:

Пример 12. Найти частное решение уравнения

Решение. Общее решение данного уравнения

При величина и при любых и , не равных одновременно нулю, первое слагаемое правой части (26) будет функцией, неограниченной при , а второе слагаемое — функцией, ограниченной при всех значениях . Следовательно, только при имеем ограниченное при решение уравнения (25), именно

Более того, решение (27) уравнения (25) ограниченно при всех :

Пример 13. Найти частное решение уравнения

удовлетворяющее условию при .

Решение. Общее решение данного уравнения

При любых значениях постоянных и , не равных одновременно нулю, решение (29) является неограниченной функцией при . При решением уравнения (28) будет функция для которой, очевидно, выполняется условие . Таким образом, функция будет искомым частным решением.

Уравнения Эйлера

Дифференциальные линейные уравнения вида

где все постоянные, называются уравнениями Эйлера . Эти уравнения заменой независимого переменного преобразуются в линейные однородные уравнения с постоянными коэффициентами:

Замечание 1. Уравнение вида

также называются уравнениями Эйлера и сводятся к линейным однородным уравнениям с постоянными коэффициентами заменой переменных .

Замечание 2. Частные решения уравнения (30) можно сразу искать в виде , при этом для к мы получаем уравнение, которое совпадает с характеристическим уравнением для уравнения (31).

Пример 1. Найти общее решение уравнения Эйлера

Решение. Первый способ. Делаем в уравнении подстановку , тогда

Корни характеристического уравнения , и общее решение уравнения будет

Но так как , то или .

Второй способ. Будем искать решение данного уравнения в виде , где — неизвестное число. Находим .

Подставляя в уравнение, получаем

Но так как , то . Корни этого уравнения . Им соответствует фундаментальная система решений , и общее решение по-прежнему будет

Неоднородные уравнения Эйлера вида

где — многочлен степени , можно также решать методом подбора по аналогии с решением неоднородного линейного дифференциального уравнения с постоянными коэффициентами и с правой частью вида .

Пример 2. Решить уравнение Эйлера

Решение. Характеристическое уравнение , или имеет корни, Поэтому общее решение соответствующего однородного уравнения будет