ТЕМА 6. Неоднородное уравнение Фредгольма 2-го рода. Уравнения Фредгольма с вырожденными ядрами. Теоремы Фредгольма.
- Алевтина Вышеславцева 5 лет назад Просмотров:
1 ТЕМА 6 Неоднородное уравнение Фредгольма -го рода Уравнения Фредгольма с вырожденными ядрами Теоремы Фредгольма Основные определения и теоремы Рассмотрим неоднородное уравнение Фредгольма yx ( ) = λ Kxs ( ) ysds ( ) + f( x) Сопряженным (союзным) интегральным уравнением называется уравнение с ядром K ( x = K( s x) Если ядро симметрическое то союзное уравнение совпадает с исходным Наряду с уравнением y( x) = λ K( x y( ds + f ( x) y = λ Ay + f будем рассматривать союзное с ним интегральное уравнение ψ ( x) = λ K ( x ψ( ds+ g( x) (в операторной форме ψ = λ A ψ + g ) g(x) — непрерывная функция Сформулируем 4 теоремы Фредгольма Теорема Однородное уравнение () ϕ( x) λ K( x ϕ( ds = и союзное с ним однородное уравнение () ψ ( x) λ K ( x ψ( ds= 4 или в операторной форме (K * (x =K(s x)) при любом фиксированном λ имеют либо только тривиальные решения либо одинаковое конечное число линейно независимых решений: ϕ ϕ ψ ψ В курсе лекций теорема была доказана для интегральных уравнений с вырожденными и симметрическими ядрами Теорема Для разрешимости неоднородного уравнения () ϕ( x) λ K( x ϕ( ds = f ( x) необходимо и достаточно чтобы f (x) была ортогональна всем линейно независимым решениям однородного союзного уравнения () ( f ( x) ψ ψ ψ если λ — характеристическое число) В курсе лекций теорема была доказана для случаев симметрических и вырожденных ядер Теорема (альтернатива Фредгольма) Либо неоднородное уравнение () разрешимо при любой неоднородности — непрерывной функции f (x) либо однородное уравнение () имеет нетривиальное решение В курсе лекций теорема была доказана для случаев симметрических и вырожденных ядер Теорема 4 Множество характеристических чисел однородного уравнения () не более чем счетно с единственной возможной предельной точкой
2 Этот результат справедлив для любого вполне непрерывного оператора В курсе лекций он был получен для вполне непрерывных самосопряженных операторов и тем самым доказан для случая симметрических ядер Для интегральных операторов с вырожденными ядрами результат тривиален Замечание В курсе лекций теоремы Фредгольма были доказаны для уравнений с симметрическими непрерывными ядрами и уравнений с непрерывными вырожденными ядрами Они справедливы и для общего случая произвольного непрерывного ядра так как имеет место следующая Теорема Интегральное уравнение Фредгольма рода y = λ Ay + f с невырожденным ядром при фиксированном λ можно заменить эквивалентным интегральным уравнением с вырожденным ядром Опишем процедуру решения неоднородного интегрального уравнения Фредгольма y( x) = λ K( x y( ds + f ( x) λay + f в случаях вырожденного ядра и симметричного ядра Напомним что ядро K ( x интегрального оператора Фредгольма называется вырожденным если оно представимо в виде K( x = ( x) ( где функции ( x) ( = непрерывны по своим аргументам на [ ] Не ограничивая общности можно считать что ( x) ( x) линейно независимы и ( ( также линейно независимы Рассмотрим уравнения Фредгольма рода yx ( ) = λ Kxs ( ) ysds ( ) + f( x) с вырожденным ядром функция K( x = ( x) ( где f (x) заданная непрерывная = Обозначив c = () s y() s ds будем иметь y( x) = λ c ( x) + f ( x) Для нахождения c получим эквивалентную систему алгебраических уравнений c = y( x) ( x) dx= λ c ( x) ( x) dx+ f( x) ( x) dx или i i i i = ki fi Обозначим определитель этой системы D( λ) = = c λ k c = f i= i i i = λk λk λk λk λk λk λk λk λk Теорема Если λ не является характеристическим числом (те D ( λ) ) то интегральное уравнение Фредгольма рода имеет решение при любой непрерывной неоднородности f (x) причем это решение единственно для каждой функции f (x) Решение алгебраической системы для c в этом случае может быть найдено например по формулам Крамера: c = D ( λ) f где D ( λ) — алгебраические i ki k D( λ ) k = ki 44
3 дополнения i-го столбца определителя D( λ ) ( D (λ) и D ( λ ) называются определителями Фредгольма) Подставляя или c в формулу y( x) = λ c ( x) + f ( x) получим yx ( ) f( x) λ D( λ) ( x) f( s ) ( sds ) = = + y ( x) = f ( x) + λ R( x s λ) f ( ds где резольвента интегрального оператора ki i k i= D( λ) k= ki R( xs λ) = Dki ( λ) i ( x) k ( D( ) λ i= k= Теперь рассмотрим интегральное уравнение Фредгольма -го рода в случае симметрического ядра Пусть ядро K ( x непрерывно по совокупности переменных симметрическое и K( x / λ — вещественное число f (x) — заданная непрерывная функция Пусть λ λ λ — последовательность характеристических чисел интегрального оператора которым соответствует ортонормированная система собственных функций ϕ ϕ ϕ (каждое характеристическое число повторяется в этой последовательности столько раз какова его кратность. ) Возможны два случая: а) λ k = Тогда решение можно записать в следующем виде λ k + λ y( x) = f ( x) f k ϕ k ( x) где fk = f() s ϕk() s ds k = λk λ — коэффициенты Фурье функции f ( x ) по ортонормированной системе собственных функций ϕ ϕ ϕ или ϕk( x) ϕk( y( x) = f( x) + λ f( ds= f( x) + λ R( x s λ) f( ds k = λk λ где k = R( x s λ ) ϕk( x) ϕk( Rxs ( λ) = — резольвента интегрального оператора Фредгольма λ λ k б) λ = λko где λ ko — характеристическое число интегрального оператора имеющее кратность r те ему отвечают r ортонормированных собственных функций ϕko( x) ϕ ko + r ( x) В этом случае решение не единственно и определяется формулой λ fk yx ( ) = f( x) + ϕk( x) + ckoϕko( x) + + cko+ r ϕko+ r ( x) λ λ k = k ko k k + r k где c ko c ko+ r — произвольные константы причем решение существует при условии ортогональности f (x) всем собственным функциям ϕko( x) ϕ ko + r ( x) соответствующим характеристическому числу λ ko Бесконечный ряд записанный в данном выражении сходится абсолютно и равномерно Заметим что решения отличаются одно от другого на функции являющиеся элементами Ker ( I λ A) (нуль-пространства) оператора I λ A Теорема А) Если однородное уравнение Фредгольма -го рода с непрерывным симметрическим ядром имеет только тривиальное решение (те λ k = ) то λ k 45
4 неоднородное уравнение имеет единственное решение для любой непрерывной функции f (x) Б) Если же однородное уравнение имеет нетривиальные решения (те λ = λk совпадает с одним из характеристических чисел) то неоднородное уравнение разрешимо в том и только том случае когда неоднородность непрерывная функция f (x) ортогональна всем собственным функциям соответствующим данному λ (ортогональна всем решениям однородного уравнения) В) В последнем случае если решение есть то оно не единственно Теорема (Альтернатива Фредгольма для интегральных уравнений Фредгольма -го рода с симметрическими ядрами): Либо неоднородное уравнение имеет решение при любой непрерывной функции f (x) либо однородное уравнение имеет нетривиальное решение Примеры решения задач Пример 6 Показать что характеристические числа однородного уравнения Фредгольма yx ( ) = λ ( s + sxysds ) ( ) и соответствующего однородного союзного уравнения ( ) = λ ( + ) ( ) zx x sxzsds совпадают и при этих λ указанные уравнения имеют одинаковое число линейно независимых решений Решение Обозначим sysds () = sy () s ds = zsds () = sz() s ds= Тогда решения указанных уравнений примут вид yx ( ) = λ+ λx zx ( ) = λx + λx и для определения коэффициентов получим λ λ = λ s ( + ds= = λ ( ) s + s ds= λ λ = λ ( s + ds= = λ s( s ds + = Итак при λ имеем = = y( x) z( x) = = при λ = остаются произвольными Поэтому λ = является характеристическим числом для обоих рассматриваемые уравнений и при этом λ они имеют по два линейно независимых решения: y( x) = y( x) = x и z( x) = x z( x) = x 46
5 Пример 6 Для каждого λ исследовать разрешимость и построить решение неоднородного уравнения Фредгольма -го рода с вырожденным несимметрическим ядром yx ( ) = λ ( s sxysds ) ( ) + x ( ) = λ ( ) ( ) sysds () = sy () s ds = тогда решение его имеет вид ( ) λ λ λ λ = λ s ( ds= = λ ( ) s s ds= Итак при Решение Рассмотрим соответствующее однородное уравнение Обозначим где yx s sxysds yx = x λ ± = = однородное уравнение имеет только тривиальное решение а значит исходное неоднородное уравнение имеет единственное решение При λ =± (характеристические числа) однородное уравнение имеет нетривиальные решения: если λ =+ то y ( x) = C если λ = то y ( x) Cx = Поэтому для указанных значений λ вопрос о разрешимости неоднородного уравнения сводится к проверке ортогональности функции f ( x) = x собственным функциям однородного союзного ( ) = λ ( ) ( ) уравнения zx x sxzsds Найдем собственные функции однородного союзного уравнения zsds () = sz() s ds= λ = λ ( s ds= При тогда решение его имеет вид λ = λ ( ) = s s s ds λ =+ получаем = — произвольно откуда f( x) z( x) dx= C x x dx= Обозначим zx ( ) = λx λx где z( x) Cx и те исследуемое уравнение разрешимо и решение его не единственно при λ = имеем = — произвольно откуда z ( x) Cx и f( x) z( x) dx= C x xdx те у исследуемого неоднородного уравнения решений нет Чтобы решить уравнения sysds () = sy() s ds= λ где = s ( λ λs+ s ) ds= снова обозначим yx ( ) = λ ( s sxysds ) ( ) + x тогда решение представимо в виде λ ( λ λ ) = s s+ s ds= + 5 yx ( ) x x = λ λ + 47
6 При λ = имеем = = следовательно решений нет как и было 5 установлено ранее при λ =+ получим = = C — произвольная постоянная поэтому 5 yx ( ) C x+ x те решение не единственно и определяется с точностью до собственной функции ядра y ( x) = C отвечающей λ = + 6 Если λ ± то = = и единственное решение дается формулой 5( + λ) 6λ x yx ( ) = + x 5( + λ) Пример 6 Построить резольвенту уравнения Фредгольма yx ( ) = λ si( x+ ysds ( ) + f( x) а) вычислив определители Фредгольма б) в виде разложения по собственным функциям однородного уравнения Решение а) Ядро исследуемого оператора K( x = si( x+ = si xcos s+ cos xsi s является вырожденным Обозначим ( six () cos () si элементы определителей Фредгольма k = ( x) ( x) dx: i i k = ( x) ( x) dx= sixcosxdx= k = ( x) ( x) dx= cosxcosxdx= k = ( x) ( x) dx= sixsixdx= k = ( ) ( ) cos si x x dx= x xdx= Вычислим определители Фредгольма: D( λ) = D( λ) = D( λ) = λ D( λ) = λk λk λk λ λk λk λk D( λ) = = = λ λ λk λk λk Искомая резольвента Rxs ( λ) = Dki ( λ) i ( x) k ( в случае D ( λ) D( λ ) i= k= те λ ± примет вид Rxs ( λ) = Dki ( λ) i ( x) k ( = D( λ ) i= k= si xcos s+ λ si xsi s+ λ cos xcos s+ cos xsi s si( x+ + λ cos( x = = λ λ 48
7 б) Характеристические числа и собственные функции однородного уравнения yx ( ) = λ si( x+ ysds ( ) были получены в примере 8: λ = и нормированная собственная функция y( x) = (six+ cos x) λ = и нормированная собственная функция y( x) = (six cos x) Подставляя их в формулу для резольвенты в случае ϕk( x) ϕk( симметрического непрерывного ядра Rxs ( λ) = имеем λ λ si( x + + λ cos( x (si x+ cos x)(si s+ cos (si x cos x)(si s cos Rxs ( λ) = + = λ λ λ Заметим что этот же результат был получен ранее методом последовательных приближений для «малого» λ (см пример 47) k = k yx ( ) = si xsi s+ s ysds ( ) + si x Пример 64 Решить уравнение ( ) Решение Обозначим si sy ( s ) ds = C sy() s ds = C тогда решение примет вид yx ( ) = ( Csi x+ C) + si x Постоянные C C могут быть найдены из системы C C C = si s ( si s+ + si ds= C C C C = s ( sis+ + si ds= C Итак C = C — остается произвольным C = C и искомое решение C определяется неоднозначно: yx ( ) = si x + (si x+ ) Замечание В рассматриваемом случае λ = совпадает с характеристическим числом однородного уравнения = λ ( + ) yx ( ) sixsi s s ysds ( ) Поэтому решение неоднородного уравнения оказалось не единственно и определилось с точностью до собственной функции соответствующего однородного уравнения отвечающей характеристическому числу λ = Действительно используя введенные выше обозначения решение однородного уравнения представим в виде yx ( ) = λ( Csi x+ C) Постоянные C C найдем из системы 49
8 C = si s λ( C si s+ C ) ds= λc C = s λ( Csi s+ C) ds= λc C( λ ) = Cλ C = нетривиальное решение которой C = C C = C существует при λ = Таким образом λ = — характеристическое число а ( ) (si ) y x = C x+ — отвечающие ему собственные функции Рекомендуем самостоятельно найти собственные функции однородного союзного уравнения zx ( ) = ( sixsi s x) zsds ( ) + и убедиться в выполнении условия разрешимости те ортогональности неоднородности f ( x) = six всем собственным функциям однородного союзного уравнения отвечающим характеристическому числу λ = Пример 65 Решение Решить уравнение Обозначим yx ( ) = xsysds ( ) + x C = sy() s ds тогда решение если оно существует можно записать в виде yx ( ) = C x+ x Подставляя это выражение в предыдущую формулу для определения постоянной C получим уравнение C = s ( C s + ds = C+ которое 5 решений не имеет Поэтому исследуемое интегральное уравнение Фредгольма yx ( ) = xsysds ( ) + xрешений также не имеет Замечание Элементарно устанавливается что λ = является характеристическим числом однородного уравнения Фредгольма yx ( ) = λ xsysds ( ) с собственной функцией y ( x) = C x Так как ядро симметрическое то λ = является также характеристическим числом однородного союзного уравнения с той же собственной функцией z ( x) = C x В рассматриваемом случае имеем λ = = λ те λ совпадает с характеристическим числом однородного уравнения При этом условие разрешимости (ортогональность неоднородности f ( x) = x всем собственным функциям однородного союзного уравнения) не выполнено 5
9 Пример 66 Рассмотрим неоднородное уравнение Фредгольма yx ( ) = λ Kxs ( ) ysds ( ) + f( x) с симметрическим непрерывным (невырожденным) ядром x ( x s K( x = s( x) s x xs [ ] ) При λ λ где λ = ( ) — собственные значения исследуемого интегрального оператора Фредгольма (см пример 77) построить резольвенту интегрального оператора и записать решение неоднородного уравнения ) Исследовать разрешимость уравнения при различных значениях λ и найти решение если оно существует в следующих случаях: а) f ( x) = si x б) f ( x) = x Решение ) Если λ λ = ( ) то используя построенную в примере 77 ортонормированную систему ϕ ( x ) = si x запишем соответствующую формулу для резольвенты интегрального оператора Фредгольма с симметрическим ядром ϕ( x) ϕ( six sis Rxs ( λ) = = = λ λ = λ Тогда решение неоднородного уравнения примет вид six sis y( x) = f( x) + λr( x s λ) f( ds= f( x) + λ f( ds = λ Меняя порядок суммирования и интегрирования в последней формуле получим решение в виде разложения в ряд по собственным функциям интегрального оператора Фредгольма с симметрическим ядром six f six y( x) = f ( x) + λ si s f ( ds = f ( x) + λ λ λ где f = = = si s f ( ds — коэффициенты Фурье по соответствующей ортонормированной системе ϕ ( x ) = si x ) Если λ λ = ( ) то неоднородное уравнение разрешимо при любой непрерывной функции f ( x ) Используя полученные выше формулы и вычисляя соответствующие интегралы имеем: si x sis si x 4 si x а) yx ( ) = si x+ λ si sds= si x+ λ = λ 4 λ 4 λ б) = + si x si s ( ) si x yx ( ) x = + λ sds= x+ λ = λ = ( λ) Если же такое что λ = λ = те λ совпадает с одним из характеристических чисел то ответ на вопрос о разрешимости уравнения зависит от конкретного вида функции f ( x ) В случае б) решение не существует ни при каких λ = λ = ( ) так как f ( x) = x при любом не ортогональна соответствующей собственной функции 5
10 ϕ ( x ) = si x однородного союзного уравнения (ядро симметрично поэтому однородное союзное уравнение совпадает с исследуемым при f( x) ) В случае а) необходимо рассмотреть два варианта При λ = 4 решение не существует так как неоднородность f ( x) = si x не ортогональна собственной функции ϕ( x) = si x однородного союзного уравнения отвечающей заданному значению λ = λ = 4 При λ = λ = 4 функция f ( x) = si x ортогональна собственной функции ϕ ( x ) = si x ( ) однородного союзного уравнения отвечающей рассматриваемому λ = λ = те решение существует но не единственно и sikx siks представимо в виде yx ( ) = si x+ sisds+ Csix где λ k= k k C — произвольная постоянная Меняя порядок суммирования и интегрирования заметим что все слагаемые в сумме при k равны нулю тк λ siks si s dx = ( k ) Поэтому учитывая что sis si sds = ( k = ) окончательно получим 4si x yx ( ) = si x + si x Csix Csix 4 + = 4 + где C — произвольно Задачи для самостоятельного решения 6 Построить резольвенту уравнений Фредгольма -го рода с симметрическим вырожденным ядром при значениях λ не совпадающих ни с одним их характеристических чисел: — через определители Фредгольма — в виде разложения по собственным функциям ядра: а) б) в) yx ( ) = λ xsysds ( ) + f( x) yx ( ) = λ ( x+ ysds ( ) + f( x) yx ( ) = λ ysds ( ) + f( x) г) yx ( ) = λ (+ cos( x ) ysds ( ) + f( x) д) yx ( ) = λ (si xsi s+ si xsi sysds ) ( ) + f( x) 6 Исследовать разрешимость при различных значениях λ и решить интегральные уравнения Фредгольма -го рода: а) yx ( ) = λ x( + ysds ( ) + x 5
11 б) в) г) д) е) ж) з) и) к ) л) yx ( ) = λ xysds ( ) + si x yx ( ) = λ (+ xsysds ) ( ) + x yx ( ) = λ xsi sysds ( ) + x s ysds x yx ( ) = λ rccos ( ) + 4 yx ( ) = λ tgs ysds ( ) + ctgx 4 yx ( ) = λ sixcos sysds ( ) + cosx yx ( ) = λ cos( x+ ysds ( ) + yx ( ) = λ ( + x ysds ( ) + si x ( ) = cos ( ) ( ) + si ( ) = λ ( + 5 ) ( ) yx λ x s ysds x yx xs xs ysds x м) yx ( ) = λ Kxs ( ) ysds ( ) + cos x где ( x + ) s x s K( x = ( s + ) x s x Ответы к задачам 6 а) б) в) г) д) xs xs Rxsλ ( ) = = λ λ λ(+ x + ( x+ Rxs ( λ) = 4λ Rxsλ ( ) = λ cos( x Rxsλ ( ) = + λ λ si xsi s+ si xsi s Rxsλ ( ) = λ 6 а) При 6 λ — единственное решение 5 x 7λ 6 yx ( ) = x + при λ = — решений нет 6 5λ 5 5
12 б) При λ — единственное решение yx ( ) = si x при λ = — yx ( ) = Cx+ si x- решение не единственно 6 в) При λ — единственное решение yx ( ) = x 7 6 при λ = — yx ( ) = x+ C(+ x) — решение не единственно 7 г) При λ — единственное решение x yx ( ) λ при λ = — решений нет д) При λ — единственное решение yx ( ) = λ + при λ = — решений нет x 8( λ) е) При всех λ — единственное решение λ yx ( ) = ctgx+ ж) При всех λ — единственное решение λ yx ( ) = cosx+ six 4λ six з) При λ ± — единственное решение yx ( ) = при λ = — решений нет + λ при λ = — yx ( ) = Ccosx six+ — решение не единственно λ и) При λ λ — единственное решение yx ( ) = si x+ x λ при λ = — решений нет x при λ = — yx ( ) = C+ si x+ — решение не единственно к) При λ λ six yx ( ) = λ при λ = — решений нет при λ = — yx ( ) = six+ C — решение не единственно 5 4 л) При λ λ — единственное решение ( ) 7 4 = + λ λ + x при λ = — решений нет при λ = — yx ( ) = + Cx x + 7x — решение не единственно 4 м) При λ λ ( ) — единственное решение x + e e (six+ cos x) yx ( ) = cosx+ λ + λ ( λ+ ) при λ = λ = — решений нет при λ = ( = 4) — решение не единственно x + e e (six+ cos x) yx ( ) = cos x+ λ C(six cos x) λ ( λ+ ) 54
Неоднородное уравнение фредгольма 2 го рода
Последние действия на сайте
Интегральное уравнение
Материал из Википедии — свободной энциклопедии
Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.
Классификация интегральных уравнений
Линейные интегральные уравнения
Это интегральные уравнения, в которые неизвестная функция входит линейно:
где 


Уравнения Фредгольма
Уравнения Фредгольма 2-го рода
Уравнения Фредгольма 2-го рода — это уравнения вида:
Пределы интегрирования могут быть как конечными, так и бесконечными. Переменные удовлетворяют неравенству: 

Ядра, удовлетворяющие последнему условию, называют фредгольмовыми. Если 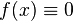
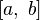
Уравнения Фредгольма 1-го рода
Уравнения Фредгольма 1-го рода выглядят также, как и уравнение Фредгольма 2-го рода, только в них отсутствует часть, содержащая неизвестную функцию вне интеграла:
при этом ядро и свободный член удовлетворяют условиям, сформулированным для уравнений Фредгольма 2-го рода.
Уравнения Вольтерра
Уравнения Вольтерра 2-го рода
Уравнения Вольтерра отличаются от уравнений Фредгольма тем, что один из пределов интегрирования в них является переменным:
Уравнения Вольтерра 1-го рода
Также, как и для уравнений Фредгольма, в уравнениях Вольтерра 1-го рода отсутствует неизвестная функция вне интеграла:
В принципе, уравнения Вольтерра можно рассматривать как частный случай уравнений Фредгольма, если переопределить ядро:
Однако некоторые свойства уравнений Вольтерра не могут быть применены к уравнениям Фредгольма.
Нелинейные уравнения
Можно придумать немыслимое многообразие нелинейных уравнений, поэтому дать им полную классификацию не представляется возможным. Вот лишь их некоторые типы, имеющие большое теоретическое и прикладное значение.
Уравнения Урысона
Постоянная M — это некоторое положительное число, которое заранее не всегда может быть определено.
Уравнения Гаммерштейна
Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:
где 
Уравнения Ляпунова — Лихтенштейна
Именами Ляпунова — Лихтенштейна принято называть уравнения, содержащие существенно нелинейные операторы, например, уравнение вида:
Нелинейное уравнение Вольтерра
где функция 
Методы решения
Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. Здесь будут рассмотрены несколько методов для решения линейных интегральных уравнений.
Преобразование Лапласа
Метод преобразования Лапласа может быть применён к интегральному уравнению, если входящий в него интеграл имеет вид свёртки двух функций:
то есть, когда ядро является функцией разности двух переменных:
Например, дано такое уравнение:
Применим преобразование Лапласа к обеим частям уравнения:

Применяя обратное преобразование Лапласа, получим:
Метод последовательных приближений
Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:
Это условие необходимо для сходимости ряда Лиувилля — Неймана:
который и является решением уравнения. (K k f)(x) — k -ая степень интегрального оператора (Kf)(x) :
Впрочем, такое решение является хорошим приближением лишь при достаточно малых | λ | .
Метод резольвент
Метод резольвент является не самым быстрым решением интегрального уравнения Фредгольма второго рода, однако иногда нельзя указать других путей решения задачи.
Если ввести следующие обозначения:
то повторными ядрами ядра 
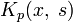
Ряд, составленный из повторных ядер,
называется резольвентой ядра 


Например, для интегрального уравнения
повторными будут следующие ядра:
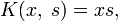
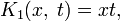

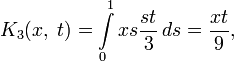
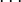
а резольвентой — функция
Тогда решение уравнения находится по формуле:
Метод сведения к алгебраическому уравнению
В случае, если ядро интегрального уравнения Фредгольма является вырожденным, то есть 
где 
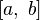
где 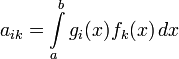

Приложения
Термин «интегральное уравнение» ввёл в 1888 году Дюбуа-Реймон, однако первые задачи с интегральными уравнениями решались и ранее. Например, в 1811 году Фурье решил задачу об обращении интеграла, которая теперь носит его имя.
Формула обращения Фурье
Задача состоит в нахождении неизвестной функции f(y) по известной функции g(x) :
Фурье получил выражение для функции f(y) :
Сведение задачи Коши к интегральному уравнению
К нелинейным интегральным уравнениям Вольтерра приводит задача Коши для обыкновенных дифференциальных уравнений:
В самом деле, это уравнение можно проинтегрировать по t от a до t :
Решение начальной задачи для линейных дифференциальных уравнений приводит к линейным интегральным уравнениям Вольтерра 2-го рода. Этим еще в 1837 году воспользовался Лиувилль. Пусть, например, поставлена задача:
Для уравнения с постоянными коэффициентами с теми же начальными условиями:
решение может быть найдено методом вариации постоянных и представлено в виде:
Тогда для исходного уравнения получается:
— интегральное уравнение Вольтерра 2-го рода.
a,» src=»http://upload.wikimedia.org/math/3/c/c/3cca9038417f8968682c783191e3f6c7.png» />
также может быть сведено к интегральному уравнению Вольтерра 2-го рода.
Задача Абеля
Исторически считается, что первой задачей, которая привела к необходимости рассмотрения интегральных уравнений, является задача Абеля. В 1823 году Абель, занимаясь обобщением задачи о таутохроне, пришёл к уравнению:
где f(x) — заданная функция, а 
У Абеля формулировка задачи выглядела примерно так:
Материальная точка под действием силы тяжести движется в вертикальной плоскости
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.
Если обозначить угол между касательной к траектории и осью Oξ как β и применить законы Ньютона, можно прийти к следующему уравнению:
http://www.sites.google.com/site/fet5486/polzovateli/filatov-d-n/integralnoe-uravnenie



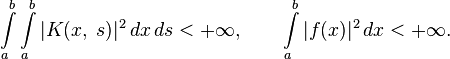
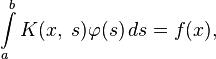
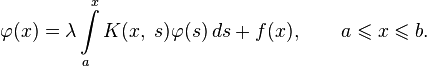
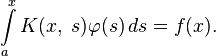

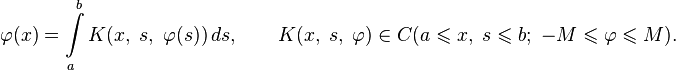

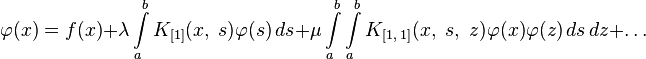

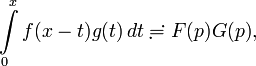
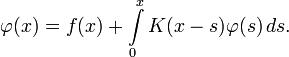

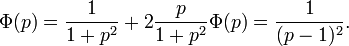
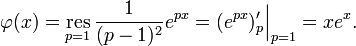


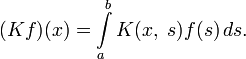
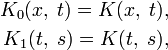





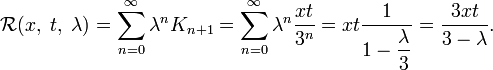


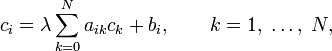

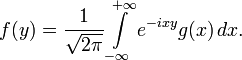

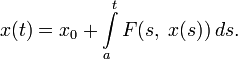

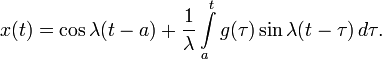
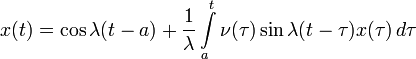
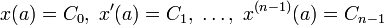

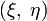 по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.