y′′+y=x 2 cos x. Пример решения линейного дифференциального уравнения со специальной неоднородной частью
Условие примера
Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами и специальной неоднородной частью в виде произведения многочлена второй степени и косинуса:
(1) .
1. Самое простое решение примера
Делаем подстановку
(1.1) ,
где i – комплексная единица, . тогда уравнение (1) примет вид:
(1.2) .
Действительно, . Все правильно.
Решаем линейное неоднородное уравнение первого порядка (1.2) с помощью интегрирующего множителя. Умножим на и выделим полный дифференциал:
;
;
.
Интегрируем:
(1.3) .
Вычисляем интеграл. Для этого, с помощью формулы Эйлера, выразим косинус через экспоненту:
.
Тогда интеграл примет вид:
(1.4)
.
Подставляем (1.5) и (1.6) в (1.4), а затем в (1.3):
;
(1.7) .
Теперь учтем, что постоянная интегрирования C является комплексным числом. Поэтому запишем ее в виде , где – действительные числа. Умножим (1.7) на . Также учтем, что согласно (1.1), :
(1.8) .
Учтем тот факт, что исходное уравнение (1) имеет действительное решение. Поэтому функции и действительные. Тогда, чтобы найти , нам нужно найти мнимую часть от выражения (1.8) справа. Выделяем действительную и мнимую части:
.
Отсюда получаем решение уравнения:
.
Преобразуем постоянные интегрирования: .
2. Стандартное решение
Теперь решим наше уравнение (1) стандартным методом. Этот метод применим для решения линейных дифференциальных уравнений n-го порядка с постоянными коэффициентами со специальной неоднородностью, которые имеют следующий вид:
,
где – многочлены степеней и , соответственно:
;
;
– известные коэффициенты.
В нашем случае, уравнение (1) второго порядка, , .
2.1 Общее решение однородного уравнения
Вначале находим общее решение однородного уравнения. Для этого отбрасываем в (1) правую неоднородную часть. Получаем однородное уравнение, в котором, чтобы не было путаницы, заменим на :
(2.1) .
Ищем решение в виде . Составляем характеристическое уравнение:
.
Оно имеет комплексные корни:
.
Им соответствует фундаментальная система решений:
.
Общее решение однородного уравнения (2.1):
.
2.2 Частное решение неоднородного уравнения
Поскольку характеристическое уравнение имеет корень кратности , и неоднородная часть имеет множитель , то частное решение Y ищем в виде
;
(2.2) .
Здесь – действительные коэффициенты, которые нужно определить.
Для определения коэффициентов , подставим частное решение (2.2) в исходное уравнение, и приравняем левую и правую части.
Найдем производные от Y . Поскольку нам нужна только производная второго порядка, то применим формулу Лейбница:
.
Сравнивая левую и правую части, получаем систему уравнений:
;
.
Решаем ее.
.
Отсюда получаем частное решение исходного уравнения:
.
Общее решение исходного уравнения:
.
3. Стандартное решение с использованием комплексных функций
3.1. Описание метода
Суть этого метода заключается в том, чтобы выполнять вычисления, используя экспоненту вместо синусов и косинусов. При таком подходе, в ряде случаев получаются более простые преобразования. При этом нам нужно использовать комплексные числа и элементарные сведения из области функций комплексного переменного.
Рассмотрим комплексную функцию , зависящую от комплексной переменной
,
где – действительные числа. Ее можно записать в виде суммы действительной и мномой частей:
,
где – действительные функции от комплексной переменной . Например:
.
Отсюда .
Далее мы будем считать, что множеством определения всех функций является множество действительных чисел. То есть будем считать, что комплексная переменная принимает только действительные значения: .
Пусть функция w является решением линейного неоднородного уравнения:
(3.1) ,
где – действительные коэффициенты (или действительные функции от действительной переменной x ); – комплексная функция; и – действительные функции. Тогда действительная u и мнимая v части функции w удовлетворяют дифференциальным уравнениям:
(3.2) ;
(3.3) .
Для доказательства подставим в (3.1):
.
Поскольку коэффициенты действительные, то, отделяя действительную и мнимую части, получаем, что функции u и v удовлетворяют дифференциальным уравнениям (3.2) и (3.3).
3.2. Применение метода
Применим этот прием к нашему уравнению (1). Возьмем комплексную функцию , и рассмотрим уравнение:
(3.4) .
Тогда действительная часть u комплексного решения этого уравнения будет удовлетворять исходному уравнению (1):
.
Для решения (3.4) мы используем стандартный метод ⇑.
3.2.1. Общее решение однородного уравнения
Находим общее решение однородного уравнения. Отбрасываем в (3.4) правую неоднородную часть. Получаем однородное уравнение:
.
Ищем решение в виде . Получаем характеристическое уравнение:
(3.5) .
Оно имеет комплексные корни
.
Им соответствует фундаментальная система решений
.
Общее решение однородного уравнения:
(3.6) ,
где и – комплексные постоянные.
Выделим в общем решении действительную и мнимую части. Для этого выразим комплексные постоянные через действительные :
.
Подставим в (3.6) и применим формулу Эйлера:
;
.
Заменим постоянные :
(3.7) .
3.2.2. Частное решение неоднородного уравнения
Находим частное решение уравнения (3.4). Неоднородная часть является экспонентой, умноженной на многочлен второй степени. Поскольку является корнем характеристического уравнения (3.5) кратности , то частное решение ищем в виде:
;
.
Находим производную второго порядка от W , применяя формулу Лейбница:
.
Дифференцируем. При этом используем обозначение:
.
Тогда ;
;
;
;
.
Сравнивая левую и правую части, получаем систему уравнений:
.
Отсюда
.
Частное решение:
.
Разделяем действительную и мнимую части:
.
Прибавляя общее решение (3.7) однородного уравнения, получаем общее решение комплексного неоднородного уравнения (3.4):
.
Отделяя действительную часть, получаем общее решение исходного уравнения (1):
.
Автор: Олег Одинцов . Опубликовано: 12-03-2021
Решение неоднородных уравнений первой степени относительно sin x и cos x
Разделы: Математика
При изучении темы «Решение тригонометрических уравнений» в курсе алгебры и начал анализа в 10 классе достаточное внимание уделяется рассмотрению примеров решений уравнений, сводящихся к квадратным и решению однородных уравнений первой и второй степени относительно sin x и cos x. При этом практически не рассматриваются примеры решения уравнений первой степени, являющихся неоднородными относительно функций sin x и cos x.
Изучая в школьном курсе 10 класса тему «Преобразование тригонометрических выражений», целесообразно ввести формулу a sinx + b cosx = 



Цели:
- ввести понятие неоднородного тригонометрического уравнения I степени;
- ознакомить с алгоритмами решения неоднородных тригонометрических уравнений I степени;
- проверить прочность усвоения ранее изученных формул тригонометрии.
Тип урока: комбинированный.
Форма проведения: индивидуальная и фронтальная работа с учащимися.
Ход урока
I. Организационный момент
Вступительное слово учителя: Изучение темы «Решение тригонометрических уравнений» кроме рассмотренного нами ранее вопроса о способах решения однородных тригонометрических уравнений I степени предполагает также рассмотрение способов решения неоднородных тригонометрических уравнений. Но прежде, чем мы перейдем к изучению нового материала, необходимо вспомнить применение формул тригонометрии при решении уравнений и неравенств.
II. Актуализация опорных знаний, умений
Математический диктант (10-12 минут).
| I вариант | II вариант | ||||||||||||
|
| ||||||||||||
| Ответы варианта I | Ответы варианта II | ||||||||||||
| (-1)
| ||||||||||||
 sin (2x + sin (2x +  ) = ) =  sin 3x sin 3x sin (2x +  ) = sin 3x ) = sin 3x sin (2x +  ) — sin 3x = 0 ) — sin 3x = 0 2 sin  cos cos  = 0 = 0 | ||
sin ( ) = 0 ) = 0 sin (  — —  ) = 0 ) = 0 x =  + 2 + 2 n, где n n, где n | или | cos ( ) = 0 ) = 0 cos (  + +  ) = 0 ) = 0 x =  + +  , где n , где n |
2) 3 sin x – 4 cos x = 5 (применение универсальной подстановки)
3
— 4
= 5
6 tg— 4 (1 — tg
) = 5 (1 + tg
)
(tg— 3)
= 0
x = 2 arctg3 + 2n, где n
3) cos x – sin x = 1 (через переход к функциям половинного аргумента)
cos 
— sin

— 2 sin
cos
= sin

+ cos


2 sin(sin
+ cos
) = 0
sin = 0
x = 2n
или sin + cos
= 0 – однородное первой степени
tg= -1
x = —+ 2
n
Для самостоятельной работы учащихся (перед началом указываются способы решения):
1) sin x + cos x = 
sin (x +
) =

sin (x +) = 1
x =+ 2
n, где n
2) 3 sin x + 5 cos x= 6 (универсальная подстановка)
3
+ 5
= 6
6 tg+5 — 5 tg

= 6 + 6 tg

11 tg
— 6 tg
+ 1= 0
решений нет, так как D 11.06.2011
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
http://urok.1sept.ru/articles/596581
http://mathdf.com/dif/ru/
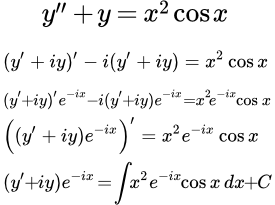
 3x =
3x = 
 —
— 
 0
0 2x =
2x = 


 +
+  ;
; 
 +
+  , n
, n 
 n; (-1)
n; (-1)
 +
+  n, n
n, n 
 n; arctg(-
n; arctg(- ) +
) +  n, n
n, n 
 +
+  n ≤ x ≤
n ≤ x ≤  +
+  n, n
n, n 
 n ≤ x ≤
n ≤ x ≤  +
+  n, n
n, n 

 +
+  ; (-1)
; (-1) 
 +
+  , n
, n 
 +
+  n;
n; 
 + 2
+ 2 n, n
n, n 
 n; arctg
n; arctg  +
+  n, n
n, n 
 +
+  ≤ x ≤
≤ x ≤  +
+  , n
, n 
 +
+  ≤ x ≤
≤ x ≤  +
+  , n
, n 


 sin(x+
sin(x+ ), где
), где  = arctg
= arctg  если a
если a  + b
+ b 
 c
c , то уравнение имеет корни
, то уравнение имеет корни cos
cos 

 — sin
— sin

 sin 3x (через введение дополнительного угла)
sin 3x (через введение дополнительного угла) — 4
— 4  = 5
= 5  — 4 (1 — tg
— 4 (1 — tg
 ) = 5 (1 + tg
) = 5 (1 + tg
 )
)  — 3)
— 3)  = 0
= 0  n, где n
n, где n

 — sin
— sin
 — 2 sin
— 2 sin cos
cos  = sin
= sin
 + cos
+ cos

 (sin
(sin  + cos
+ cos ) = 0
) = 0 = 0
= 0  n
n + cos
+ cos  = 0 – однородное первой степени
= 0 – однородное первой степени  = -1
= -1  + 2
+ 2 n
n sin (x +
sin (x +  ) =
) = 
 ) = 1
) = 1  + 2
+ 2 n, где n
n, где n
 + 5
+ 5  = 6
= 6  +5 — 5 tg
+5 — 5 tg
 = 6 + 6 tg
= 6 + 6 tg


 — 6 tg
— 6 tg  + 1= 0
+ 1= 0