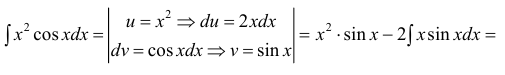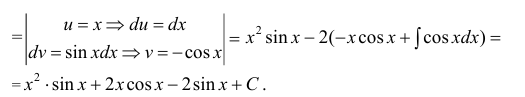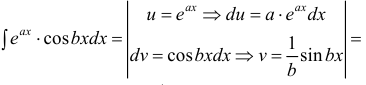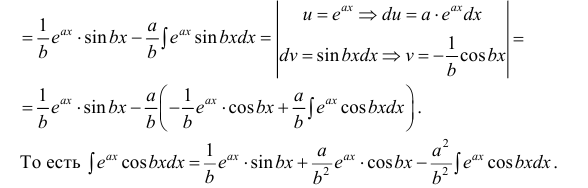Методы интегрирования неопределенного интеграла с примерами решения
Содержание:
При решении многих практических задач таких, как вычисление длин линий, площадей, отыскание траекторий движения и других, вводится понятие интегрирования.
Определения
Определение: Первообразной функции
Теорема: (о существовании первообразной) Если функция f(x) непрерывна на сегменте 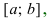
Теорема: Если F(x) — первообразная функции f(х), то функция F(x) + C (С -произвольная постоянная) также является первообразной функции f(х).
Доказательство:
ТЗ. Если 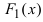
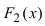
Доказательство: Пусть 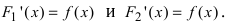
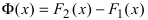
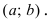
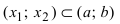
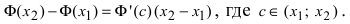
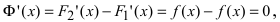
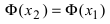
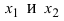
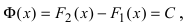
Пример:
Пусть дана функция 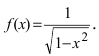
Решение:
В случае наличия двух первообразных показать, что они отличаются на постоянную величину.
Для функции существуют две первообразные 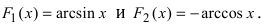
Определение: Совокупность всех первообразных функции 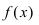
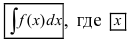
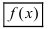
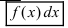
На основании теорем можно записать, что
Определение: Отыскание всех первообразных называется неопределенным интегрированием.
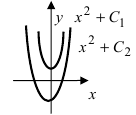
Выясним геометрический смысл неопределенного интеграла. Пусть дана функция 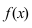
Пример:
Построить кривые, которые задаются неопределенным интегралом
Решение:
Первообразной для под интегральной функции f(х) = 2х будет функция 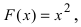
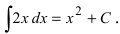
Рис. 1. Интегральные кривые
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна под интегральной функции
Доказательство: По определению неопределенного интеграла
2. Дифференциал неопределенного интеграла равен под интегральному выра- жению
Доказательство: По определению дифференциала от неопределенного интеграла имеем
3. Если под интегральное выражение является дифференциалом некоторой функции F(x), тo неопределенный интеграл равен
Доказательство: Так как
4. Неопределенный интеграл от линейной комбинации функций равен той же самой линейной комбинации неопределенных интегралов от этих функций
- а) неопределенный интеграл от суммы (разности) функций равен сумме (разности) неопределенных интегралов от этих функций
- б) постоянный множитель можно выносить за знак неопределенного интеграла
5. Формула неопределенного интеграла не зависит от обозначения переменной интегрирования
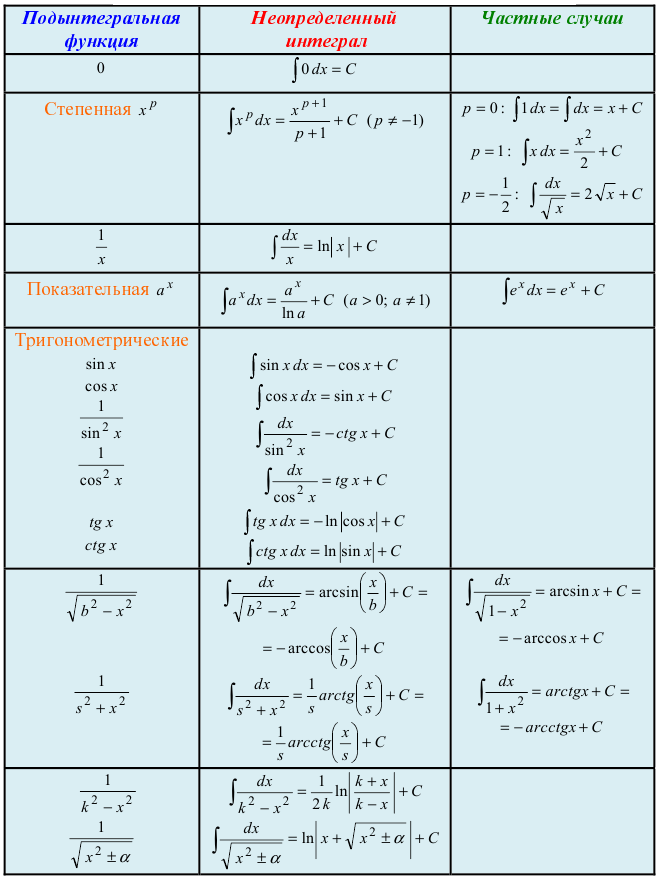
Таблица основных неопределенных интегралов
Методы интегрирования
Метод тождественных преобразований под интегральной функции
Данный метод основан на использовании простых приемов, алгебраических и тригонометрических формул, свойств подынтегральной функции, разложения полиномов на простые множители и свойств неопределенного интеграла. Рассмотрим этот метод на конкретных примерах.
1. Почленное деление числителя дроби на ее знаменатель
Замечание: Следует запомнить, что нет формулы почленного деления знаменателя дроби на ее числитель, т.е.
Пример:
Найти
Решение:
Выполним в под интегральной функции почленное деление числителя дроби на ее знаменатель и воспользуемся свойством линейности неопределенного интеграла
Замечание: Из этого примера видно, что слова «найти неопределенный интеграл” означают: за счет преобразований подынтегральной функции и использования свойств неопределенного интеграла данный интеграл надо привести к совокупности табличных интегралов и воспользоваться этой таблицей.
Замечание: Из примера также видно, что, несмотря на наличие двух табличных интегралов, константа интегрирования С пишется один раз, так как сумма или разность постоянных интегрирования все равно есть постоянная величина.
2. Использование противоположных арифметических операций (например, сложение-вычитание).
Пример:
Найти
Решение:
Анализ под интегральной функции показывает, что в числитель дроби надо добавить и вычесть 1 (при этом подынтегральная функция не изменится), а затем воспользоваться первым приемом (почленное деление числителя дроби на ее знаменатель)
3. Использование алгебраических и тригонометрических формул, например,
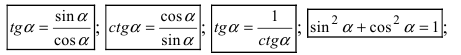
Пример:
Найти
Решение:
Воспользуемся формулой квадрата разности
Пример:
Найти
Решение:
4. Использование свойств функций, например,
Пример:
Вычислить
Решение:
Пример:
Вычислить
Решение:
5. Использование разложения полиномов на простые множители, например, 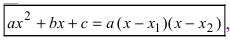
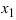
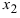
Пример:
Найти
Решение:
По теореме Виета уравнение 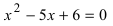
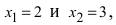
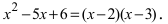
Метод замены переменной интегрирования
Данный метод основан на формуле
Метод замены переменной интегрирования применяется в двух случаях:
а) Если аргумент функции отличается от простого аргумента х, то этот сложный аргумент принимается в качестве новой переменной интегрирования t.
Пример:
Вычислить
Решение:
Так как показатель степени экспоненты отличается от простого аргумента х, то этот показатель степени принимаем в качестве новой переменной интегрирования, т.е.
Замечание: После нахождения первообразной с новой переменной интегрирования надо обязательно вернуться к старой переменной интегрирования.
Пример:
Вычислить
Решение:
Выражение, стоящее в круглых скобках, является аргументом степенной функции и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е.
Пример:
Вычислить
Решение:
Выражение, стоящее в круглых скобках, является аргументом функции синус и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е. 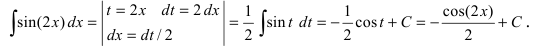
Пример:
Найти
Решение:
В подынтегральном выражении содержится элементарная функция tgx и в качестве множителя при dx присутствует ее первая производная 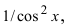
Пример:
Найти
Решение:
Данный пример объединяет первый метод с методом замены переменной интегрирования. Выполним почленное деление числителя дроби на ее знаменатель и разобьем интеграл на два интеграла, для которых применяются два случая замены переменной интегрирования
Замечание: Умение отыскивать подходящую замену вырабатывается в процессе многократных упражнений, однако можно указать ряд случаев, когда можно сразу увидеть необходимую замену переменной интегрирования при анализе подынтегрального выражения, например, 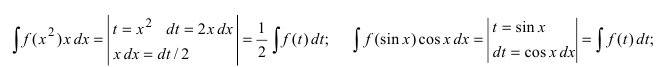
Метод интегрирования по частям
Интегрирование по частям основано на использовании формулы дифференциала от произведения двух функций 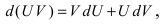
Таким образом, для неопределенного интеграла формула интегрирования по частям имеет вид:
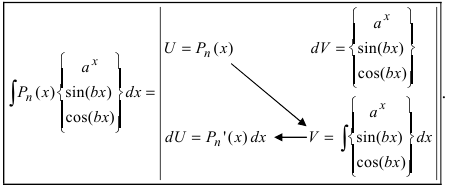
Для того чтобы знать, какую из функций принимать за U (все остальное в подынтегральном выражении принимается за dV), рассмотрим наиболее часто встречающиеся случаи:
1. 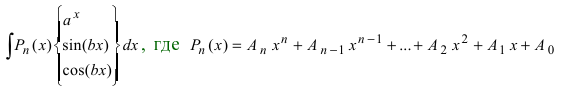
В этом случае
Замечание: Для нахождения функции dU используют определение дифференциала функции. При вычислении функции V интегрируют выражение dV, при этом постоянная интегрирования полагается равной нулю (С = 0). После выполнения этих действий применяют формулу интегрирования по частям.
Пример:
Вычислить
Решение:
Применим метод интегрирования по частям
Замечание: Из приведенного примера видно, что при необходимости метод интегрирования по частям применяется повторно.
2. Для интегралов вида
Пример:
Вычислить
Решение:
Действуя согласно методике, получим
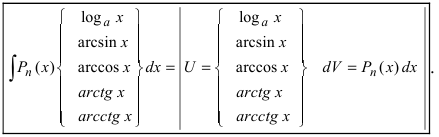
3. Для интегралов вида 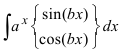
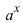
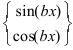
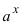
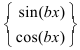
Пример:
Найти
Решение:
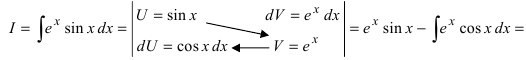
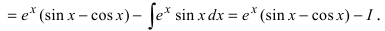
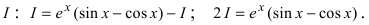
4. Нестандартные интегралы требуют для своего вычисления приобретения опыта на практических занятиях.
Пример:
Найти
Решение:
Неопределенный интеграл
Определение 1. Пусть Δ − промежуток действительной оси. Функция y=F(x) называется первообразной для функции y=f(x) на промежутке Δ, если F(x) − дифференцируема на Δ и 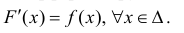
Пример:
а) F(x)=x − первообразная для 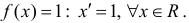
б) 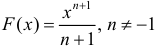
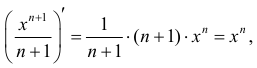
в) 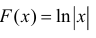
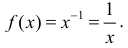
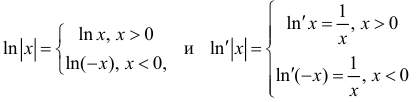
Замечание. Первообразная функция определена не однозначно. А именно,
F(x) = x+C , где С – любая константа также будет первообразной для 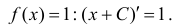
В общем случае верна теорема:
Теорема 1. Две дифференцируемые на промежутке Δ функции 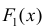
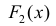
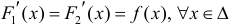
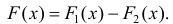
Тогда 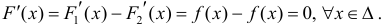
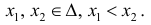
По теореме Лагранжа (теорема 4 § 12): 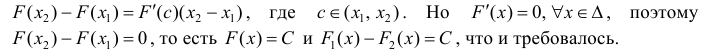
Достаточность. 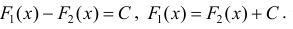
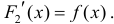
Тогда 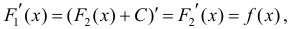
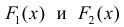
для одной и той же функции y=f(x), что и требовалось доказать.
Определение 2. Множество всех первообразных для функции y=f(x) на промежутке Δ называется неопределенным интегралом от функции f(x) и обозначается 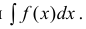
Если F(x) — одна из первообразных, то , согласно теореме 1, 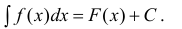
Свойства неопределенного интеграла
- Если ( ) F x — дифференцируема на Δ , то
(3) или
(4) здесь под записью
подразумеваем одну из первообразных.
- Если f (x) имеет первообразную на Δ, то λf(x) также имеет первообразную на Δ и ,если λ ≠ 0, то
(5)
- Если
имеют первообразную на Δ , тогда
также имеет первообразную на Δ и:
(6)
Свойства 1 – 4 легко выводятся из определения первообразной и интеграла
и соответствующих свойств производной.
Докажем, например, свойство 3.
Пусть F (x) — первообразная для f (x) на промежутке Δ. Тогда 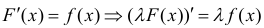
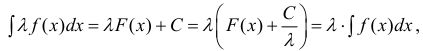
Из определений 1,2 следует, что интегрирование – действие обратное
дифференцированию (находится функция, производная которой равна данной).
Таблица интегралов
При вычислении интегралов в простых случаях применяют свойства 1 – 4.
Пример:
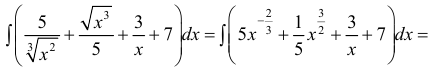
Пример:
Теорема 1. Если y=f(x) — непрерывна на промежутке Δ , то для нее ∃ первообразная функция y = F(x) на этом промежутке.
Замена переменной в неопределенном интеграле
Теорема 1. Пусть функция y = F(t) — первообразная для функции y = f(t) на промежутке 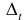
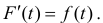
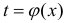
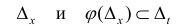
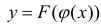
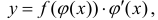
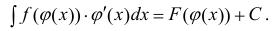
Доказательство. 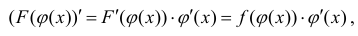
Замечание. Формулу (1) можно переписать в виде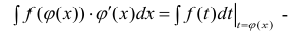
формула интегрирования с помощью подстановки 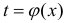
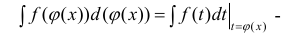
Формула интегрирования с помощью поднесения под дифференциал, когда
подынтегральную функцию 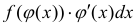
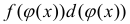
занося 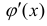
Пример:
Пример:
Пример:
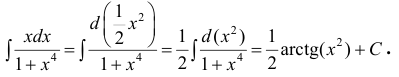
При поднесении под дифференциал можно использовать свойства
дифференциала (см. § 6) 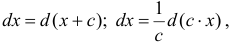
Пример:
Пример:
Пример:
Иногда в формуле (2) легче вычислять левую часть, чем правую:
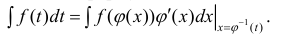
Формула (5) – формула интегрирования с помощью замены переменной 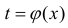
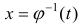
Пример:
Интегрирование по частям в неопределенном интеграле
Теорема 1. Пусть функция u(x) и v(x) – дифференцируемы на промежутке Δ и на этом промежутке 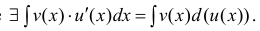
∃ и 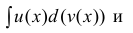
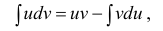
Доказательство. 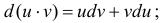
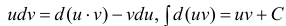
Пример:
Пример:
Замечание.
- При интегрировании выражений вида:
— многочлен степени n полагают:
После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).
- При интегрирования выражений вида:
полагают:
(
— многочлен). После интегрирования по частям интеграл упрощается.
Пример:
Пример:
Таким образом, проинтегрировав дважды по частям, получили уравнение,
содержащее 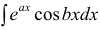
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Определённый интеграл
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R»
- Неопределённый интеграл
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Неопределенный интеграл в дифференциальном уравнении
pdf Лекция 1 . Первообразная и ее свойства. Неопределенный интеграл, его свойства, связь с дифференциалом. Таблица основных неопределенных интегралов.
pdf Лекция 2 . Интегрирование подстановкой и заменой переменной. Интегрирование по частям. Интегрирование выражений, содержащих квадратный трехчлен.
pdf Лекция 3 . Рациональные дроби. Разложение правильной рациональной дроби на сумму простейших (без д-ва). Интегрирование простейших дробей. Интегрирование правильных и неправильных рациональных дробей.
pdf Лекция 4 . Интегрирование выражений, рационально зависимых от тригонометрических функций. Интегрирование иррациональных функций. Примеры интегралов, не выражающихся через элементарные функции.
pdf Лекции 5-6 . Определенный интеграл как предел интегральных сумм. Теорема об интегрируемости кусочнонепрерывной функции (без д-ва). Геометрическая интерпретация определенного интеграла. Основные свойства определенного интеграла. Теоремы об оценке и о среднем значении.
pdf Лекция 7 . Определенный интеграл с переменным верхним пределом и теорема о его производной. Формула Ньютона-Лейбница. Вычисление определенных интегралов подстановкой и по частям. Интегрирование периодических функций, интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат.
Модуль 2 — «Приложения определенного интеграла»
pdf Лекция 8 . Несобственные интегралы по бесконечному промежутку (1-го рода). Несобственные интегралы от неограниченных функций на отрезке (2-го рода). Признаки сходимости несобственных интегралов. Абсолютная и условная сходимости. Несобственные интегралы с несколькими особенностями.
pdf Лекции 9-10 . Признаки сходимости несобственных интегралов. Абсолютная и условная сходимости. Несобственные интегралы с несколькими особенностями.
pdf Лекция 11 . Вычисление площадей плоских фигур, ограниченных кривыми, заданными в декартовых координатах, параметрическии и в полярных координатах.
pdf Лекции 12-13 . Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения. Вычисление длины дуги и площади поверхности вращения. Метод Симпсона приближенного вычисления определенного интеграла.
Модуль 3 — «ОДУ первого порядка»
pdf Лекция 14 . Задачи, приводящие к дифференциальным уравнениям. Дифференциальное уравнение первого порядка, его решения. Частные и общие решения. Интегральные кривые. Понятие частной производной функции нескольких переменных. Задача Коши для дифференциального уравнения первого порядка. Теорема Коши о существовании решения дифференциального уравнения.
pdf Лекция 15 . Решение дифференциальных уравнений первого порядка: с разделяющимися переменными, однородных, линейных, Бернулли.
pdf Лекция 16 . Геометрическая интерпретация дифференциального уравнения первого порядка. Изоклины. Геометрическое решение дифференциальных уравнений с помощью изоклин. Особые точки и особые решения дифференциального уравнения первого порядка.
pdf Лекция 17 . Дифференциальные уравнения n-го порядка. Частные и общие решения. Задача Коши и ее геометрическая интерпретация (n=2). Теорема Коши о существовании и единственности решения дифференциального уравнения (без док-ва). Краевая задача. Понижение порядка некоторых типов дифференциальных уравнений n-го порядка.
Модуль 4 — «ОДУ высших порядков»
pdf Лекции 18-19 . Линейные дифференциальные уравнения n-го порядка, однородные и неоднородные. Теорема существования и единственности решения. Дифференциальный оператор L[y], его свойства. Линейное пространство решений однородного линейного дифференциального уравнения. Линейная зависимость и независимость системы функций на промежутке. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно независимых решений однородного линейного дифференциального уравнения. Теорема о структуре общего решения однородного линейного дифференциального уравнения. Размерность пространства решений однородного линейного дифференциального уравнения. Фундаментальная система решений однородного линейного дифференциального уравнения. Формула Остроградского-Лиувилля и ее следствия. Понижение порядка однородного линейного уравнения (при известном частном решении).
pdf Лекции 20-21 . Линейные однородные уравнения с постоянными коэффициентами. Характеристическое уравнение линейного однородного дифференциального уравнения. Построение общего решения по корням характеристического уравнения (вывод для n=2). Линейные неоднородные дифференциальные уравнения. Структура общего решения линейного неоднородного дифференциального уравнения. Теорема о наложении частных решений. Метод Лагранжа вариации постоянных (вывод для n=2). Структура частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами и правой частью специального вида.
pdf Лекция 22 . Нормальные системы дифференциальных уравнений. Автономные системы дифференциальных уравнений. Фазовое пространство и фазовые траектории. Задача и теорема Коши. Частные и общее решения. Сведение дифференциального уравнения высшего порядка к нормальной системе дифференциальных уравнений первого порядка. Сведение нормальной системы к дифференциальному уравнению высшего порядка (вывод для n=2). Первые интегралы системы. Понижение порядка системы дифференциальных уравнений при помощи первых интегралов. Интегрируемые комбинации. Симметрическая форма записи нормальной автономной системы дифференциальных уравнений.
pdf Лекция 23 . Системы линейных дифференциальных уравнений первого порядка. Определитель Вронского. Фундаментальная система решений. Формула Остроградского-Лиувилля. Теоремы о структуре общего решения однородной и неоднородной систем линейных дифференциальных уравнений. Метод вариации произвольных постоянных.
pdf Лекция 24 . Однородные системы линейных дифференциальных уравнений с постоянными коэффициентами. Характеристическое уравнение системы. Построение общего решения по корням характеристического уравнения (вывод только для случая действительных и различных корней).
Интегралы Дифференциальные уравнения — реферат
Основные вопросы лекции: первообразная; неопределенный интеграл, его свойства; таблица интегралов; методы интегрирования: разложение, замена переменной, по частям; интегрирование рациональных функций; интегрирование иррациональностей и выражений, содержащих тригонометрические функции, задачи, приводящие к понятию определенного интеграла; интегральная сумма; понятие определенного интеграла, его свойства; определенный интеграл как функция верхнего предела; формула Ньютона Лейбница; применение определенного интеграла к вычислению площадей плоских фигур; вычисление объемов тел и длин дуг кривых; несобственные интегралы с бесконечными пределами и от неограниченных функций, основные понятия дифференциальных уравнений; задача Коши; дифференциальные уравнения с разделяющимися переменными; однородные дифференциальные уравнения 1-го порядка; линейные дифференциальные уравнения 1-го порядка, дифференциальные уравнения 2-го порядка, допускающие понижение порядка; линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами: однородные и неоднородные.
Функция 



Теорема. Если 







Множество всех первообразных для функции 






Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции, то есть

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, то есть

где 
4. Постоянный множитель можно выносить за знак интеграла, то есть
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, то есть

Метод замены переменной

где 
Метод интегрирования по частям

где 

Интегрирование рациональных дробей. Простейшими дробями называют дроби вида


причем квадратный трехчлен не имеет действительных корней.
Рациональную функцию 
Для интегралов вида 


При интегрировании тригонометрических выражений 



Талица основных интегралов.
1. 
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Пусть на отрезке 










будем называть интегральной суммой для функции 





Пусть предел интегральной суммы при стремлении 










Экономический смысл интеграла. Если 







Достаточное условие существования интеграла. Теорема. Если 

Свойства определенного интеграла.
1. Постоянный множитель можно выносить за знак интеграла, то есть

где 

2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, то есть

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, то есть при любых
4. Если на отрезке 



Следствие. Пусть на отрезке 





Теорема о среднем. Если функция 




Теорема. Пусть функция 







Эта формула называется формулой Ньютона – Лейбница.
Теорема. Пусть функция 






Тогда имеет место равенство


Эта формула носит название формулы замены переменной в определенном интеграле.
Теорема. Пусть функции 



Эта формула называется формулой интегрирования по частям.
Теорема. Пусть на отрезке 







Пусть на отрезке 






Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции.
Дифференциальное уравнение 

Решением дифференциального уравнение называется такая функция 
Общим решением дифференциального уравнения 

которое является функцией переменных 


Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных 
Теорема. Пусть в дифференциальном уравнении

функция 


1. Для любой точки 



2. Если два решения 



Дифференциальное уравнение (1) первого порядка называется неполным, если функция 


Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде

где 





Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид

где 


В случае, когда функция 
Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

где 

Если 

называется однородным, в противном случае при 
Теорема. Если 


Для некоторых действительных чисел 


называется характеристическим уравнением уравнения (3).
1. Пусть характеристическое уравнение (4) имеет действительные корни 


где 

2. Если характеристическое уравнение (4) имеет один корень 

где 

3. Если характеристическое уравнение (4) не имеет действительных корней, то общее решение уравнения (3) имеет вид

где 



Теорема. Общее решение линейного неоднородного дифференциального уравнения (2) равно сумме общего решения соответствующего однородного уравнения (3) и частного решения исходного неоднородного уравнения (2).
Числовым рядом называется выражение вида

Числа 

Сумма 


Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, то есть
Число 
Свойства сходящихся рядов.
1. Если ряд (1) сходится и имеет сумму 



сходятся и их суммы соответственно равны 



3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания или приписывания конечного числа членов.
Теорема (необходимый признак сходимости) Если ряд сходится, то предел его общего члена стремится к нулю, то есть

Теорема (признак сравнения). Пусть (1) и (2) – ряды с положительными членами, причем члены первого ряда не превосходят членов второго, то есть при любом

Тогда а) если сходится ряд (2), то сходится и ряд (1)
б) если расходится ряд (1), то расходится и ряд (2).
Теорема (предельный признак сравнения). Пусть (1) и (2) – ряды с положительными членами и существует конечный предел отношения их общих членов 
Теорема (признак Даламбера). Пусть дан ряд (1) с положительными членами и существует предел

Тогда, если 


Ряды с членами произвольного знака
Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд в котором члены попеременно то положительны то отрицательны
Теорема. (Признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине и предел его общего члена при 
Если ряд, составленный из абсолютных величин членов данного ряда (1) сходится, то сходится и данный ряд.
Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.
Степенным рядом называется ряд вида

Совокупность тех значений 
Теорема Абеля. 1). Если степенной ряд сходится при значении 






1. 
2. 
Тогда областью сходимости степенного ряда будет интервал 
На любом отрезке 


Кроме того, в интервале сходимости степенной ряд можно почленно дифференцировать. При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости 
Имеют место следующие разложения элементарных функций.


Основные вопросы лекции: случайные события; случайные величины, описательный подход к понятию случайной величины, дискретные случайные величины, случайные величины общего вида, функция распределения, распределение случайных величиныи числовые характеристики.
Числовые характеристики случайных величин
Рассмотрим основные характеристики дискретной случайной величины при конечном числе значений.
Каждому значению дискретной случайной величины отвечает его вероятность. Как отмечалось выше, последовательность таких пар образует ряд распределения дискретной случайной величины:
где 


Если случайная дискретная величина является случайной альтернативной величиной, т.е. задается двумя значениями 0 и 1 и соответствующими им вероятностями исходов q = 1 – ри р, то ряд распределения принимает форму:

где 0 ≤ p ≤ 1, p + q = 1.
На основе ряда распределения можно определить среднее значение случайной дискретной величины как меру, которая объединяет значения случайной дискретной величины и их вероятности. Среднее значение есть взвешенная средняя всех возможных значений случайной величины, роль весов (частот) играют вероятности.
Ожидаемое среднее значение случайной величины называется математическим ожиданием М(Х) (оценкой, которую ожидают получить).
Математическое ожидание случайной дискретной величины X (т.е. принимающей только конечное или счетное множество значений x1, x2,…, хп соответственно с вероятностями р1, p2,…, рп) равно сумме произведений значений случайной величины на соответствующие им вероятности:

Свойства математического ожидания случайной дискретной величины
Математическое ожидание случайной дискретной величины обладает следующими свойствами:
где С – постоянная величина.
где С – постоянная величина.
3. М (Х1 ± Х2 ±…± Хn) = М(Х1) ± М(Х2) ±…± М(Хn). (2)
4. Для конечного числа пнезависимых случайных величин:
М (Х1∙ Х2∙…∙Хn)= М(Х1) ∙М(Х2) ∙…∙М(Хn). (3)
Следствие. Математическое ожидание отклонения значений случайной величины X от ее математического ожидания равно нулю:
6. Математическое ожидание среднего арифметического значения п одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию каждой из величин:

Случайные дискретные величины называются одинаково распределенными, если у них одинаковые ряды распределения, а следовательно, и одинаковые числовые характеристики.
Пусть Х1, Х2,…, Хn – одинаково распределенные случайные величины, математические ожидания каждой из которых одинаковы и равны а. Тогда математическое ожидание их суммы равно nаи математическое ожидание средней арифметической равно а:

Ожидаемое среднее значение функции случайной величиныожидаемое среднее значение можно вычислять как функцию случайной величины. Пусть h(X) – функция случайной величины X. Ожидаемое значение функции дискретной случайной величины:

Функция h(X) может быть любой, например X 2,3Х 4, logX. Разберем простой пример, когда h(X) – линейная функция от X, т.е. h(X)= аХ+ b, где а, b – числовые параметры.
Ожидаемый ежемесячный доход от продаж продукции составляет 5400 условных денежных единиц. Для линейной функции случайной величины вычисления M[(h(x)] можно упростить, так как из свойств математического ожидания следует, что
где a, b – числовые параметры.
Формула (5) подходит для любых случайных величин как дискретных, так и непрерывных.
Дисперсия дискретной случайной величины
Дисперсия случайной величины есть математическое ожидание квадрата отклонения значений случайной величины от ее математического ожидания.
σ2 = D(X) = M <[X – M(X)] 2>= 
Вероятности значений случайной величины играют роль весов (частот) при вычислении ожидаемых значений квадратов отклонений дискретной случайной величины от средней. По формуле (7) дисперсия вычисляется путем вычитания математического ожидания из каждого значения случайной величины, затем возведения в квадрат результатов, умножения их на вероятности Р(хi) и сложения результатов для всех хi.
Для примера 3.1 (о рекламных объявлениях, размещаемых в газете в определенный день) дисперсия вычисляется так:
σ2 = 
Свойства дисперсии дискретной случайной величины
Дисперсия дискретной случайной величины обладает следующими свойствами.
где C – постоянная величина.
где C – постоянный множитель.
3. Для конечного числа nнезависимых случайных величин:
D (X1 ± Х2±…±Xn) = D(X1) + D(X2)+ … +D(Xn). (8)
4. Если Х1, Х2,…, Хn – одинаково распределенные независимые случайные величины, дисперсия каждой из которых равна σ2 (Хi), то дисперсия их суммы равна пσ2, а дисперсия средней арифметической равна σ2/п:

Для вычисления дисперсии проще пользоваться другой формулой, полученной путем несложных математических выкладок:
D(X) = M[X – M(X)] 2 =M[X2 – 2M(X) X+ M(X) 2] =
M(X) 2 –2M(X) M(X) + [M(X)] 2 = M(X2) – [M(X)] 2 = M (X 2) – М 2 (Х).
Таким образом, σ2 = D(X) = M(X2) – М2 (Х). (10)
Дисперсия линейной функции случайной величины
Для случайной величины, заданной линейной функцией аХ+b, имеем
D(a∙X+ b)= a2∙D(X)=a2∙σ2. (11)
По формуле (11) найдем дисперсию ожидаемого дохода для примера 3. Доход задан функцией 2Х-8000. Находим M(X2)=50002∙0,2 + 60002∙0,3 + 70002∙0,2 + 80002∙0,2 + 90002∙0,1 =4 650 000. М(Х)=6700. Отсюда дисперсия D(X)=M(X2) – [М(Х)] 2=46 500 000 – 67002=1 610 000. Используя формулу (11), вычислим дисперсию ожидаемого дохода: D(Х) = σ2 = 22∙1 610 000 = 6 440 000. Среднее квадратическое отклонение дохода равно
Испытания Бернулли – это последовательность n идентичных испытаний, удовлетворяющих следующим условиям:
1. Каждое испытание имеет два исхода: успех и неуспех – взаимно несовместные и противоположные события.
2 Вероятность успеха р остается постоянной от испытания к испытанию. Вероятность неуспеха q = 1-р.
3. Все n испытаний – независимы. Вероятность наступления события в любом из испытаний не зависит от результатов других испытаний.
Успех и неуспех – статистические термины. Например, когда имеют дело с производственным процессом, то исход испытания «деталь дефектная» определяют как успех. Успех относится к появлению определенного события – «деталь дефектная», а неуспех относится к непоявлению события. Определим случайную величину как биномиальную, если для нее мы рассчитываем число успехов и неуспехов в последовательности n испытаний Бернулли.
Случайная величина, для которой вычисляется число успехов в n повторных испытаниях, где р – вероятность успеха в любом из заданных испытаний, a q = (1-р) – соответствующая вероятность неуспеха, подчиняется закону биномиального распределения с параметрами n и р.
Все возможные исходы данного эксперимента называются элементарными событиями, а множества составленные из них – событиями. Таким образом можно разбить все множество исходов на благоприятствующие данному событию (то есть входящие в него) и не благоприятствующие. Множество всех исходов обозначают 
Классическое определение вероятности. Вероятностью события 


где 


Пусть некоторый эксперимент повторяется 
Схема Бернулли имеет место при соблюдении трех условий.
1. Каждое повторение имеет два исхода.
2. Повторения независимы.
3. Вероятность появления события постоянна и не меняется при повторениях.
Тогда вероятность появления события 



где 



Если события 
1. попарно не пересекаются, то есть 
2. 
то говорят что они образуют полную группу событий.
Теорема (формула полной вероятности). Если 



Теорема (формула Байеса) Если 



Случайной величиной называют любую числовую функцию заданную на множестве 
Дискретной случайной величиной называется случайная величина принимающая не более чем счетное число значений. Дискретную случайную величину удобно задавать в виде таблицы
 |  |  |  |  |
 |  |  |  |  |
где 


Математическим ожиданием 



Свойства математического ожидания
1.
2.
3. 
Дисперсией 
1.
2.
3. 
Среднеквадратическим отклонением 

Функцией распределения случайной величины называют функцию 
Свойства функции распределения
1. 
2. Функция 
3. Функция 
Случайная величина называется непрерывной, если непрерывна ее функция распределения. Плотностью распределения 
1.
2.
3.
Для непрерывных случайных величин математическое ожидание определяется как число 
На практике чаще всего встречаются следующие виды распределений
1.Биномиальное, где случайная величина принимает значения 

2.Геометрическое, где случайная величина принимает значения 
3.Нормальное, где плотность распределения имеет вид
4.Равномерное, где плотность распределения имеет вид

1. Высшая математика для экономистов: Учебник для вузов / Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2003.
2.Е.С. Кочетков, С.О. Смерчинская Теория вероятностей в задачах и упражнениях / М. ИНФРА-М 2005.
3. Высшая математика для экономистов: Практикум / Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2004.Ч1, 2
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., Высшая школа, 1977
5. Гмурман В.Е. Теория вероятностей и математическая статистика. М., Высшая школа, 1977
6. М.С. Красс Математика для экономических специальностей: Учебник/ М. ИНФРА-М 1998.
7. Выгодский М.Я. Справочник по высшей математике. – М., 2000.
8.Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1971.
9.А.К. Казашев Сборник задач по высшей математике для экономистов – Алматы — 2002 г.
10.Пискунов Н.С. Дифференциальное и интегральное исчисление. – М.: Наука, 1985, Т1,2.
11.П.Е. Данко, А.Г. Попов, Т.Я. Кожевников Высшая математика в упражнениях и задачах/ М. ОНИКС-2005.
12.И.А. Зайцев Высшая математика/ М. Высшая школа-1991 г.
13.Головина Л.И. Линейная алгебра и некоторые ее приложения. – М.: Наука, 1985.
14.Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы анализа экономики. – М.: ДИС, 1997.
15.Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. – М.: Высшая школа, 1982 – Ч 1, 2.
16.Колесников А.Н. Краткий курс математики для экономистов. – М.: Инфра-М, 1997.
http://fn.bmstu.ru/educational-work-fs-12/70-lections/241-int
http://www.sinref.ru/razdel/03100matematica/04/382726.htm
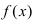
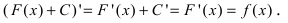
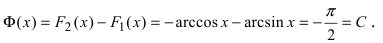
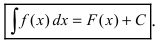
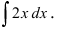
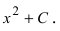
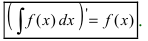
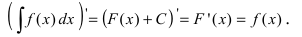
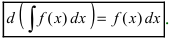
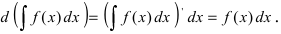
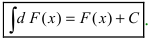
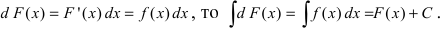
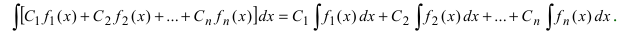
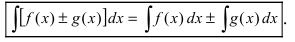
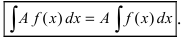
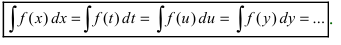
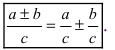
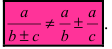
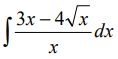
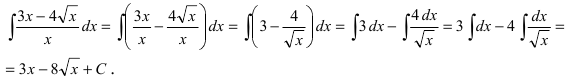
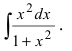
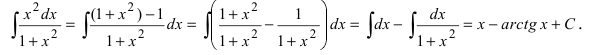
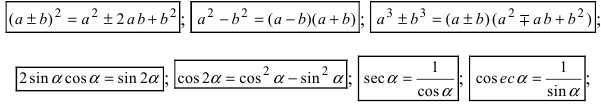
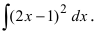
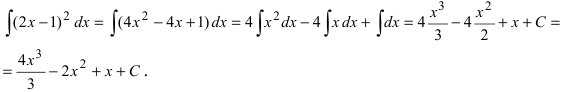
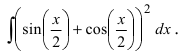
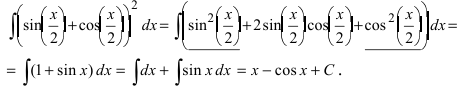
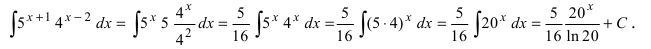
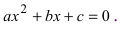
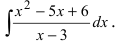
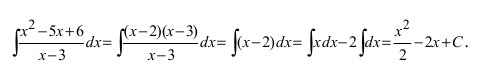
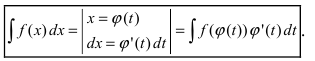
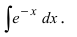
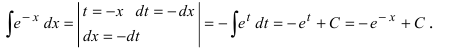
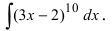
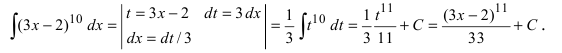
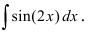
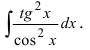
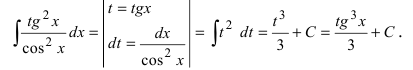
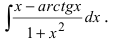
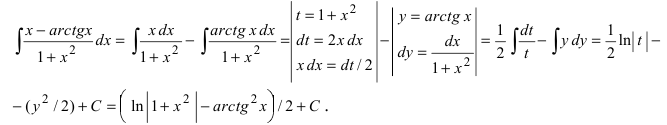
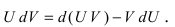
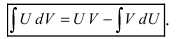
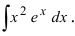
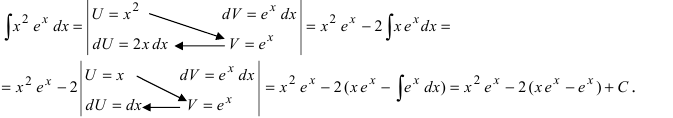
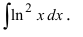
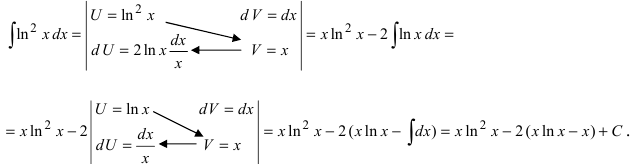
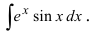
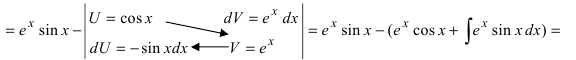
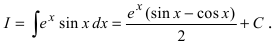
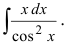
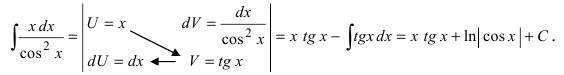
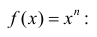
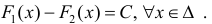
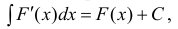 (3) или
(3) или 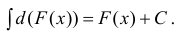
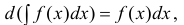 (4) здесь под записью
(4) здесь под записью 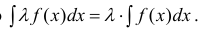 (5)
(5)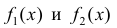 имеют первообразную на Δ , тогда
имеют первообразную на Δ , тогда 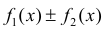 также имеет первообразную на Δ и:
также имеет первообразную на Δ и: 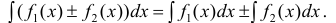 (6)
(6)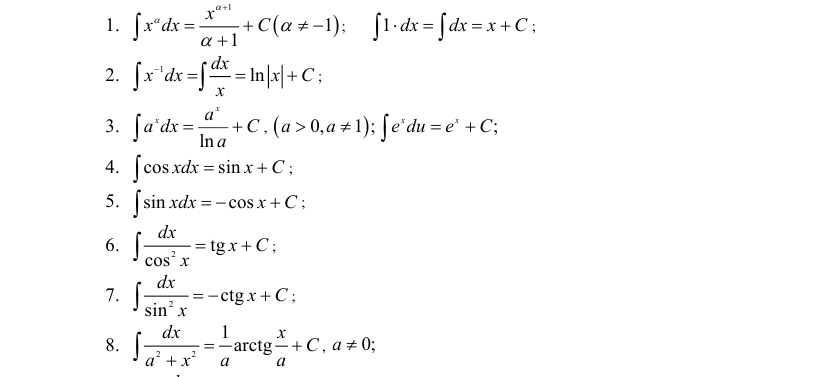
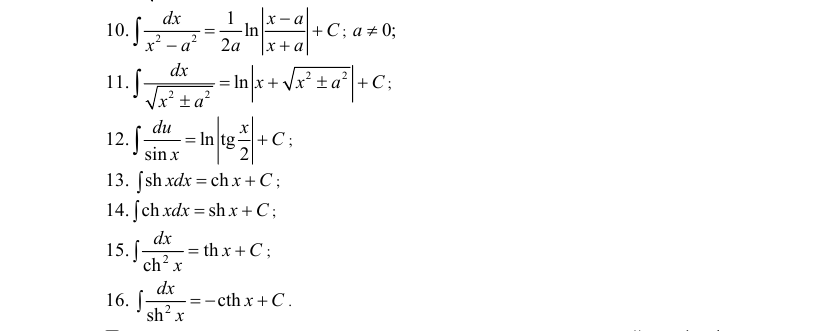
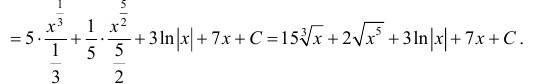
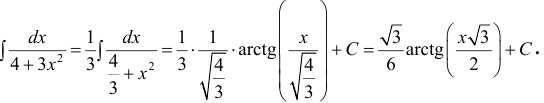
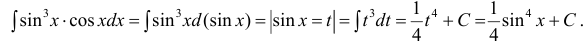
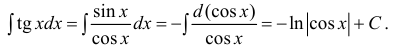
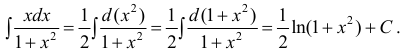
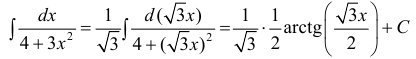
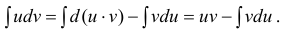
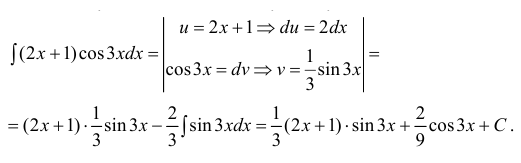
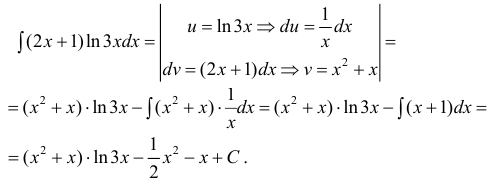
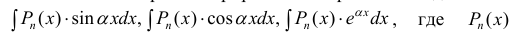 — многочлен степени n полагают:
— многочлен степени n полагают: 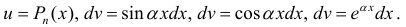 После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).
После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).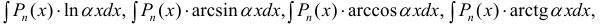
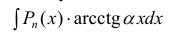 полагают:
полагают: 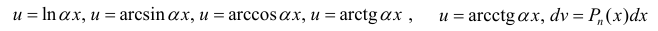 (
(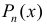 — многочлен). После интегрирования по частям интеграл упрощается.
— многочлен). После интегрирования по частям интеграл упрощается.