Неполные квадратные уравнения с параметром примеры

Методика обучения решению квадратных уравнений с параметром

Разделы: Математика

Решение задач с параметром вызывает затруднения у учащихся, так как практических заданий по данной теме в школьных учебниках недостаточно.

Цели разработки темы

• формирование устойчивого интереса к познавательному процессу при изучении математики и оценка возможности овладения предметом с точки зрения дальнейшей перспективы;
• обеспечение прочного и сознательного усвоения учащимися системой математических знаний, умений и навыков;
• формирование качества мышления, характерного для математической деятельности и необходимые человеку для жизни в современном обществе;
• выявление и развитие математических способностей учащихся.
• Задачи разработки темы:
• показать универсальные алгоритмы для решения квадратных уравнений с параметром;
• научить приемам решения различного класса задач с параметром, способствовать овладению технических и интеллектуальных математических умений на уровне свободного их использования;
• использование новых современных педагогических технологий обучения.

В математике параметр – это постоянная величина, выраженная буквой, сохраняющая свое постоянное значение лишь в условиях данной задачи (“параметр” с греческого “parametron” – отмеривающий)..

Если ставится задача для каждого значения параметра а из некоторого числового множества А решить уравнение F(х;а)= 0 относительно х, то это уравнение называют уравнением с переменной х и параметром а, а множество А – областью изменения параметра. Под областью определения уравнения F(х;а)=0 с параметром а понимаются такие системы значений х и а, при которых F(х;а) имеет смысл. Все значения параметра а, при которых F(х;а) не имеет смысла, включать в число значений параметра, при которых уравнение не имеет решений. Под областью изменения параметра (если не сделано специальных оговорок) берется множество всех действительных чисел, а задачу решения уравнения с параметром формулировать следующим образом: решить уравнение F(х;а)=0 (с переменной х и параметром а) – это значит на множестве действительных чисел решить семейство уравнений, получающихся из данного уравнения при всех действительных значениях параметра или установить, что решений нет.

В связи с тем, что выписать каждое уравнение из бесконечного семейства уравнений невозможно, но каждое уравнение семейства должно быть решено, следовательно, необходимо по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества и решить затем заданное уравнение на каждом из этих подмножеств. Для разбиения множества значений параметра на подмножества, удобно пользоваться теми значениями параметра, при которых или при переходе через которые происходят качественные изменения уравнения. Такие значения параметра называются контрольными.

1. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ

Задачи с параметрами можно разделить на два больших класса:

• задачи, в которых необходимо при всех значениях параметра из некоторого множества решить уравнение;
• задачи, в которых требуется найти все значения параметра, при каждом из которых решение уравнения удовлетворяют некоторым условиям.

В зависимости от типа задачи изменяется и вид ответа. В первом случае в решении и ответе должны быть рассмотрены все возможные значения параметров. Если хотя бы одно значение какого-либо параметра не исследовано, решение задачи не может быть признано полным.

Во втором случае в ответе перечисляются только те значения параметра, при которых выполнены условия задачи, а при решении подобных задач обычно решать заданное уравнение нет необходимости.

Уравнение вида Ах 2 + Вх + С= 0 , где А, В, С — выражения, зависимые от параметра, х – переменная — называется квадратным уравнением с параметром.

Уравнение вида ах 2 +вх+с=0, где , а, в, с – действительные числа, называют квадратным уравнением. D=в 2 -4ас называется дискриминантом квадратного уравнения (“дискриминант” по – латыни “различитель”).

В зависимости от значения дискриминанта возможны три случая:

D > 0. Данное квадратное уравнение имеет два действительных корня

D=0. Данное уравнение имеет корень двойной кратности

D 2 +2кх+с=0 со вторым коэффициентом (в=2к) четным, для нахождения корней удобно пользоваться формулами: , где D₁= =к 2 -ас.

№ 1.1. Определите все значения параметра а при которых уравнение ах 2 +2(а+1)х+а+3=0 имеет два неравных корня.

Если а=0, то имеем 0·х 2 +2(0+1)х+0+3=0, 2х+3=0 — данное уравнение является линейным, х=-1,5 – единственный корень. Итак, а=0 не удовлетворяет условию задачи.

Если а?0, то уравнение имеет два различных корня, когда дискриминант >0.

Найдем=(а+1) 2 -а(а+3)=-а+1,-а+1>0, а 2 -4(а+1)х+4а+1=0 имеет один корень.

Если а=0, то имеем 2·0·х 2 -4(0+1)х+4·0+1=0, -4х+1=0 — данное уравнение является линейным, х=0,25 – единственный корень. Итак, а=0 удовлетворяет условию задачи.

Если а 0, то исходное уравнение является квадратным и имеет единственный корень при =0. Найдем =(2(a+1)) 2 -2a(4а+1) = -4a 2 +6a+4,4a 2 +6a+4=0, а₁=2, а₂=-0,5.

С учетом а=0, запишем ответ: а=-0,5, а=0, а=2.

№ 1.3. При каких значениях параметра а квадратное уравнение (5а-1)х 2 -(5а+2)х+3а-2=0 не имеет корней?

Если 5а-1=0,а=0,2, то имеем (5*0,2-1)х 2 -(5*0,2+2)х+3*0,2-2=0,

-3х-1,4=0 — данное уравнение является линейным, х = — единственный корень.

Итак, а=0,2 не удовлетворяет условию задачи.

Если а 0,2, то квадратное уравнение не имеет корней, если дискриминант квадратного уравнения D 2 -4(5a-1)(3а-2)=-35a 2 +72a-4,-35a 2 +72a-4 2 -72a+4>0, а₁=2, а₂=, (а-2)(а-)>0. С учетом а 0,2 ответ:

№ 1.4. Определите все значения параметра а при которых уравнение (2а-1)х 2 +ах+2а-3=0 имеет не более одного решения.

Если 2а-1=0,а=0,5, то имеем (2·0,5-1)х 2 +0,5·х+2·0,5-3=0, 0,5х-2=0 — данное уравнение является линейным, х=4 — единственный корень.

Итак, а=0,5 удовлетворяет условию задачи.

Если а 0,5, то квадратное уравнение имеет не более одного решения, если дискриминант квадратного уравнения D0.

Найдем D=а 2 -4(2a-1)(2а-3)=-15a 2 +32a-12, -15a 2 +32a-120,

15a 2 -32a+12?0, а₁=, а₂=, (а-)(а-) 0.

С учетом а 0,5, имеем .

С учетом а=0,5, запишем ответ: .

2. НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ.

Квадратное уравнение ах 2 +вх+с=0, где а 0 называется неполным, если хотя бы один из коэффициентов в или с равен 0.

Общая схема решения неполных квадратных уравнений с параметрами.

ах 2 =0, где а 0, в=0, с=0. Если а 0 ,то уравнение примет вид: х 2 =0, х=0.

Следовательно, уравнение имеет два совпадающих корня, равных нулю.

Если а=0, то х — любое действительное число.

ах 2 +с=0, где а0, в=0, с0. Если а0,то уравнение примет вид: следовательно, уравнение имеет корни, то они равны по абсолютной величине, но противоположны по знаку; 2 +вх=0, где а0, в0, с=0. Если а0,то уравнение примет вид: х(а+в)=0,или Если а=0, то вх=0, х=0.

№ 2.1. При каких значениях параметра а оба корня уравнения 2х 2 +(3а 2 -|а|)х-а 2 -3а=0 равны нулю?

Оба корня квадратного уравнения равны нулю, когда

№ 2.2. При каких значениях параметра а, корни уравнения 2 х 2 -(5а-3)х+1=0 равны по модулю, но противоположны по знаку?

Корни квадратного уравнения равны по модулю, но противоположны по знаку, когда 5а-3=0,а=0,6, но с учетом того, что имеем уравнение 2х 2 +1=0, х 2 =-0,5, которое корней не имеет. Ответ: .

№ 2.3. При каких значениях параметра а один из двух различных корней уравнения 3х 2 +х+2а-3=0 равен нулю?

Параметр должен удовлетворять условию: 2а-3=0, а=1,5. Ответ: а=1,5.

№ 2.4. При каких значениях параметра а корни уравнения 3х 2 +(а 2 -4а)х+а-1=0 равны по модулю, но противоположны по знаку?

Корни квадратного уравнения равны по модулю, но противоположны по знаку, когда:

Ответ: а=0.

№ 2.5. Решить относительно х неполное квадратное уравнение х 2 -2а+1=а.

х 2 =а+2а-1; х 2 =3а-1.

Если 3а-1=0, а= ,то уравнение имеет два совпадающих корня, равных нулю.

Если 3а-1 0. а>, то уравнение имеет два корня .

Ответ: при арешений нет; при а= х=0; при

3. ИССЛЕДОВАНИЕ И РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ.

№ 3.1. Исследовать и решить уравнение с параметром х 2 –2(а-1)х+2а+1=0.

Найдем дискриминант: D=(а — 1) 2 -2а – 1= а 2 -2а+1-2а-1= а 2 — 4а.

D > 0, а 2 — 4а > 0, а (а -4) > 0, а 4, то уравнение имеет два действительных корня ;

D =0, а (а-4)=0, а=0, то х=а-1, х=0-1, х=-1, а=4,то х=а-1, х=4-1, х=3;

D 2 +2(а+1)х+а–2= 0.

1) При а-1=0, а=1 имеем линейное уравнение 4х-1=0, х=– единственное решение.

2) При а 1 уравнение является квадратным, найдем дискриминант:

D₁ = (а+1) 2 -(а–1)(2а-2)=а 2 +2а+1-а 2 +2а+а-2=5а-1.

D₁>0. 5а-1>0, а>, а 1, то уравнение имеет два корня .

D₁=0. 5а-1=0, а=, то уравнение имеет два равных корня .

х 2 +2х-8–ах+4а=0; х 2 +(2-а)х+4а-8=0. Уравнение является квадратным.

Найдем дискриминант: D=(2-а) 2 -4(4а-8)=4-4а+а 2 -16а+32= а 2 -20а+36.

D>0. а 2 20а+36>0, (а-18)(а -2)>0, а 18, то уравнение имеет два действительных корня .

D=0. (а-18)(а-2)=0, а=2, то ; а=18, то ;

D 2 равен 1, то уравнение принимает вид х 2 +px+q, где p и q — некоторые числа называется приведенным квадратным уравнением.

Теорема Виета: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

ах 2 +вх+с=0, где х₁ и х₂ – корни квадратного уравнения, то

Справедливо утверждение, обратное теореме Виета.

Теорема: Если числа p и q таковы, что их сумма равна -p, а произведение равно q. то эти числа являются корнями уравнения х 2 +px+q=0.

№ 4.1. При каком значении параметра а сумма обратных величин действительных корней уравнения 2х 2 -2ах+а 2 -2=0 равна ?

Пусть х₁ и х₂ – корни квадратного уравнения, по условию _.

По теореме Виета: Используя соотношения между корнями и условие задачи, имеем:

Найдем дискриминант квадратного уравнения:

Имеем: Ответ: при

№ 4.2. В уравнении (а 2 -5а+3)х 2 +(3а-1)х+2=0 определите а так, чтобы один из корней был вдвое больше другого.

Пусть х₁ и х₂ – корни квадратного уравнения, по условию х₁ =2 х_2. Заметим, что кратное сравнение выполняется только для положительных чисел.

По теореме Виета и условию задачи имеем систему:

Составим и решим уравнение:

Можно вычислить дискриминант данного уравнения, а затем проверить, удовлетворяет ли данное значение параметра а условию, что дискриминант неотрицателен, а так же, что корни положительны. Однако в данной задаче значительно проще сделать проверку, подставив это значение а в исходное уравнение.

При Корни отрицательны и кратно не сравниваются, поэтому задача решений не имеет. Ответ: решений нет.

№ 4.3. Найти все значения параметра а, при которых квадратное уравнение (а+2)х 2 –ах-а=0 имеет два корня, расположенных на числовой прямой симметрично относительно точки х=1.

При а+2=0, а=-2, то 2х+2=0, х=-1 – единственное решение, следовательно данное значение а не удовлетворяет условию задачи.

При а-2. Пусть х₁ и х₂ – корни квадратного уравнения, по условию х₁ =1-у, х_2.=1+у, где у – некоторое действительное число.

По теореме Виета имеем:

Решим первое уравнение системы: 2(а+2)=а, а=-4.

Найдем дискриминант данного квадратного уравнения:

Данное значение а=-4 удовлетворяет полученным значениям. Ответ: а=-4.

Ответ: при а = — 4.

1. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.
2. Азаров А.И., Барвенов С.А., Федосенко В.С. Методы решения задач с параметрами. Минск; “Аверсэв”. 2005.
3. Амелькин В. В., Рабцевич В. Л. Задачи с параметрами. Минск; “Асар”. 1996.
4. Данкова И. Н., Бондаренко Т. Е., Емелина Л. Л., Плетнева О. К.Предпрофильная подготовка учащихся 9 классов по математике. Москва; “5 за знания”.2006.
5. Литвиненко В. Н., Мордкович А. Г.. Практикум по элементарной математике. Москва; “Просвещение”.1991.
6. Родионов Е. М. Решение задач с параметрами. Москва; “Русь – 90”. 1995.
7. Студенецкая В. Н., Сагателова Л. С. Математика 8 – 9классы: сборник элективных курсов. Волгоград; “Учитель”. 2006.
8. Шарыгин И. Ф. Решение задач. Москва; “Просвещение”. 1994.
9. Шахмейстер А. Х. Уравнения и неравенства с параметрами. Санкт-Петербург; “Петроглиф”. 2006.

Индивидуальный проект по теме » Уравнения второй степени с параметрами и к ним сводимые»

Проект по математике

Скачать:

Предварительный просмотр:

Муниципальное казенное общеобразовательное учреждение

Петропавловская средняя общеобразовательная школа

Секция: техническое направление, ИКТ в образовании

Уравнения второй степени с параметром и к ним сводимые

Выполнил: Дьяченко Наталья Евгеньевна, ученица X «Б» класса

Руководитель: Грякалова Лариса Георгиевна, учитель математики

ПАСПОРТ ПРОЕКТНОЙ РАБОТЫ

Название: «Уравнения второй степени с параметром и к ним сводимые»

Автор проекта: Дьяченко Наталья Евгеньевна , ученица X «Б» класса

Научный руководитель: Грякалова Лариса Георгиевна, учитель математики

Цель работы: систематизировать знания о решении уравнений второй степени с параметром, к ним сводимых уравнений и составить алгоритм их решения.

1) Дать определение понятию «уравнение с параметром»;

2) Показать принцип решения уравнений второй степени с параметром на общих случаях;

3) Показать решение уравнений второй степени с параметрами, используя аналитический метод;

4) Составить алгоритм решения уравнений с параметрами.

Этапы проектной работы:

1. Были выделены различные типы уравнений второй степени с параметром: неполные квадратные уравнения, приведённые квадратные уравнения и другие квадратные уравнения с параметром;
2. Были выделены более сложные типы задач: уравнения второй степени с параметром с дополнительными условиями, дробно-рациональные уравнения с параметром, сводимые к уравнениям второй степени и другие;
3. Были подобраны и решены примеры уравнений каждого типа.

В результате проектной работы был получен алгоритм решения уравнений второй степени с параметром и к ним сводимых.

ВВЕДЕНИЕ

Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами («параметр» с греч. parametron – отмеривающий). В обыденной жизни мы употребляем слово «параметр» как величину, характеризующую какое-либо основное свойство процесса, явления или системы, машины, прибора (напряжение, электрическое сопротивление, масса, коэффициент трения и др.).

В математике параметр – это постоянная величина, выраженная буквой, сохраняющая свое постоянное значение лишь в условиях данной задачи. При математическом моделировании различных процессов часто возникают задачи с параметрами (уравнения или неравенства, системы уравнений и неравенств, построение семейства кривых). В курсе элементарной математики уравнения и неравенства с параметрами являются, пожалуй, самыми сложными задачами. Обычно мы встречаем линейные уравнения с параметром, и только иногда квадратные уравнения с тем же параметром. Поэтому у меня возникло желание разобраться в этой теме: уравнения второй степени с параметрами, дополнив её уравнениями, сводимыми к выше названным.

Данная тема актуальна, потому что нам может пригодится умение решать уравнения второй степени с параметрами при сдаче экзамена ЕГЭ по математике и при поступлении в высшие учебные заведения.

Гипотеза работы: количество корней и их значение будет зависеть от значения параметра.

Цель работы: систематизировать знания о решении уравнений второй степени с параметром, к ним сводимых уравнений и составить алгоритм их решения.

Для достижения поставленной цели необходимо решить следующие задачи:

1) дать определение понятию «уравнение с параметром»;

2) показать принцип решения уравнений второй степени с параметром на общих случаях;

3) показать решение уравнений второй степени с параметрами, используя аналитический метод;

4) составить алгоритм решения уравнений с параметрами.

Для выполнения поставленной цели были использованы следующие методы: использование литературы разного типа, и работа на занятиях по математике.

Объектом исследовательской работы было решение уравнений второй степени с параметрами.

РАЗДЕЛ 1: ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РЕШЕНИЯ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ С ПАРАМЕТРОМ

Если в выражении с двумя неизвестными x и a, переменной a придавать какое-либо фиксированное значение, то это уравнение (или неравенство) можно рассматривать как задачу с одной переменной x . Множеством решения такой задачи является множество пар чисел x и a , при подстановке которых в исходное выражение получается верное равенство (или верное неравенство). Аргументы x и a считаются неравноправными, так как при решении задач обычно стараются найти x , выраженное через a . Далее необходимо выяснить зависимость решений от значений параметра a , что является важной частью решения задачи. Иногда ее называют исследованием и отделяют от непосредственного решения. Решить уравнение с параметром а – это значит для каждого значения а найти значения х , удовлетворяющие этому уравнению.

В квадратных уравнениях вида a +bx+c=0 , где x –переменная, параметр является коэффициентом или частью коэффициента.

Задачи с параметрами можно разделить на два больших класса: задачи, в которых необходимо при всех значениях параметра из некоторого множества решить уравнение; задачи, в которых требуется найти все значения параметра, при каждом из которых решение уравнения удовлетворяют некоторым условиям. В итоге мы получаем алгоритм решения уравнений второй степени с параметром:

1. Привести уравнение второй степени к виду , где a, b и c – коэффициенты, x – переменная.
2. Определить область допустимых значений параметра и переменной.
3. Обратить внимание на коэффициент а , если здесь находится параметр, то следует рассмотреть случай, где a=0: уравнение вида ax^2+bx+c=0 , станет уравнением вида bx+c=0 .
4. Найти дискриминант: D= -4ac (или , где ). Он будет выражен через параметр. Как известно, от знака дискриминанта будет зависеть количество корней:

Если D >0, то уравнение имеет два корня ,

Если D = 0, то уравнение имеет один корень ,

1. Найденные контрольные значения параметра разбивают область допустимых значений параметра на промежутки. На каждом из промежутков нужно определить знак дискриминанта и посчитать значения переменной.

РАЗДЕЛ 2: ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ, СОДЕРЖАЩИХ ПАРАМЕТР

2.1 НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ

Квадратное уравнение ах^2+bх +с=0 , где а≠ 0 называется неполным, если хотя бы один из коэффициентов b или c равен 0.

Общая схема решения неполных квадратных уравнений с параметрами:

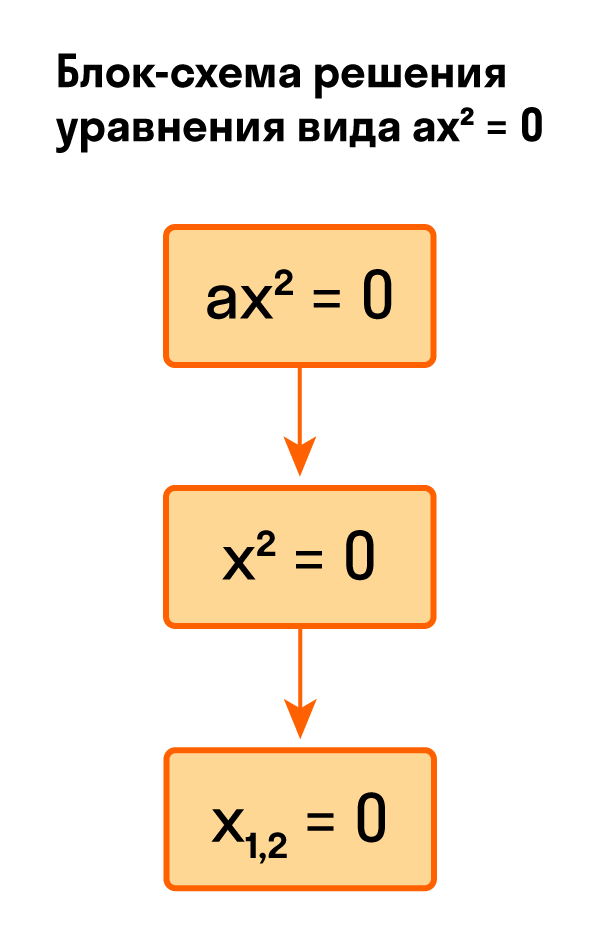
• ах^2=0, где а≠ 0, b=0, с=0 . Если а≠0 ,то уравнение примет вид: х^2=0, х=0 .

Следовательно, уравнение имеет два совпадающих корня, равных нулю.

Если а=0, то х — любое действительное число.

• ах^2+с=0, где а≠0, b=0, с≠0 . Если а≠0 ,то уравнение примет вид:

. Если , ,следовательно, уравнение имеет корни, они равны по абсолютной величине, но противоположны по знаку. Если , следовательно, уравнение корней не имеет. Если а=0 и с≠0, то уравнение действительных корней не имеет.

• ах^2+bх=0, где а≠0, b≠0, с=0 . Если a ≠0,то уравнение примет вид:

, и . Если a=0 , то bх=0, х=0.

Рассмотрим это на примере: х^2-2а+1=а, x – переменная, a–параметр.

Коэффициенты: a=1, b=0, c= -3a+1

если , , то нет корней — .

Ответ: при нет корней; при x=0; при .

2.2 ПРИВЕДЁННЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ

Приведённое квадратное уравнение – это уравнение вида a + bx+c=0, где a=1.

При решении приведённых квадратных уравнений с параметром нужно:

1. Рассмотреть случай, где параметр равен нулю .
2. Найти дискриминант: D= -4ac .
3. Если D>0, то уравнение имеет два корня

Если D=0, то уравнение имеет один корень

Решим уравнение , x – переменная, a – параметр.

Ответ: при любом а,

Решим уравнение , x–переменная, m – параметр.

Ответ: если , то нет корней; если , то

2.3 УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ С ПАРАМЕТРОМ

При решении уравнений второй степени будем пользоваться планом, предоставленным в теоретическом разделе.

Решим уравнение , где y – переменная, m – параметр.

При любом m, D 0

Ответ: при любом m, .

2.4 УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ С ПАРАМЕТРОМ С ДОПОЛНИТЕЛЬНЫМИ УСЛОВИЯМИ

Дополнительные условия могут формулироваться так:

• При каком значении параметра уравнение имеет один/ два/ и более корня (не имеет корней)
• При каком значении параметра один (оба корня) равны нулю
• При каком значении параметра корни равны по модулю, но противоположны по знаку
• При каком значении параметра уравнения имеют хотя бы один общий корень и пр.

При решении таких уравнений используются известные формулы для корней квадратного уравнения, теорема Виета и условия существования действительных решений – знак дискриминанта.

Решим уравнение: , где х – переменная, а – параметр.

При каких значениях параметра a уравнение:

1. имеет два различных действительных корня;
2. имеет один корень;
3. не имеет действительных корней;
4. имеет один из корней равный нулю;
5. имеет оба корня равных нулю;
6. имеет корни равные по модулю, но противоположные по знаку?

если , , то нет корней

если a=0, то нет корней

1. и
2. Уравнение должно иметь вид , где

1. Уравнение должно иметь вид где

Система не имеет решений.

Таких значений параметра нет.

1. Уравнение должно иметь вид где

Таких значений параметра нет.

e) Таких значений параметра нет.

f) Таких значений параметра нет.

ПРИМЕНЕНИЕ ТЕОРЕМЫ ВИЕТА

Теорема Виета гласит: для того чтобы числа и были корнями уравнения , необходимо и достаточно выполнения равенств:

Решим уравнение, используя теорему Виета.

При каком a уравнение имеет два различных отрицательных корня?

Оба корня будут отрицательными, если тогда

2.5 ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ, СВОДИМЫЕ К УРАВНЕНИЯМ ВТОРОЙ СТЕПЕНИ

Когда мы решаем дробно-рациональное уравнение, первым делом нужно его преобразовать. Если полученное уравнение является уравнением второй степени с параметром, исследуем его и решаем уравнение с параметром, учитывая область допустимых значений.

Неполные квадратные уравнения

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

• если D 0, есть два различных корня.

Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.