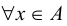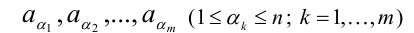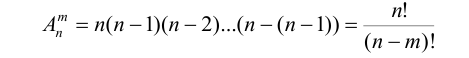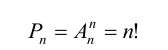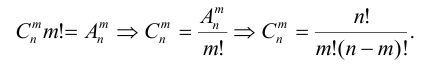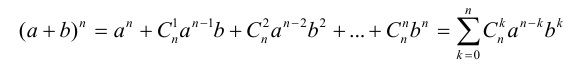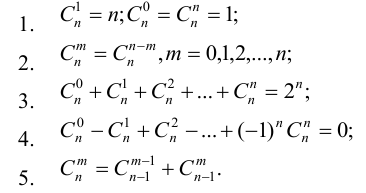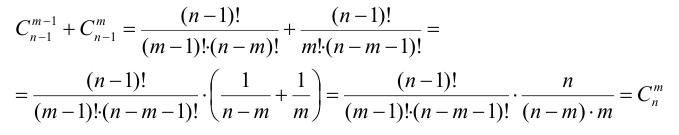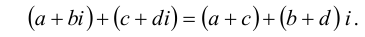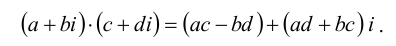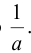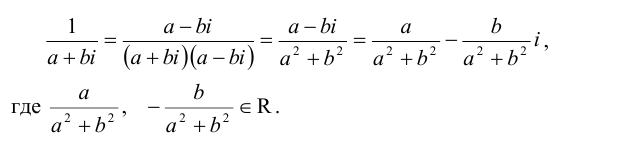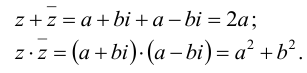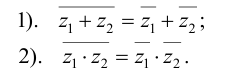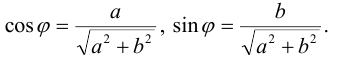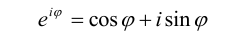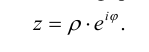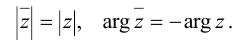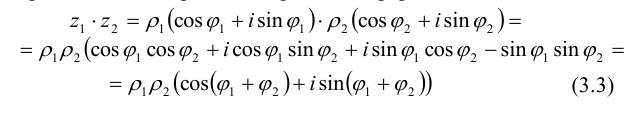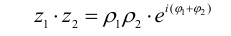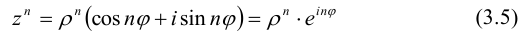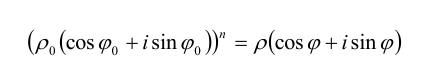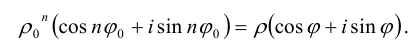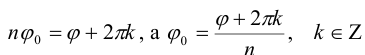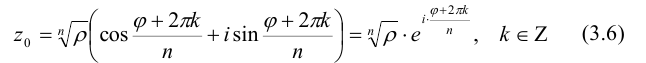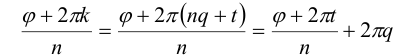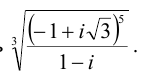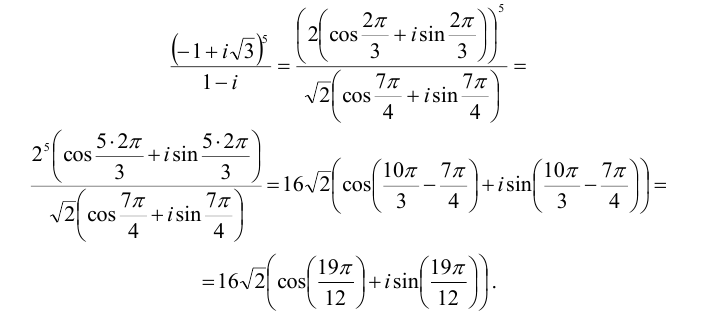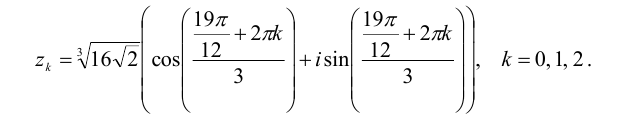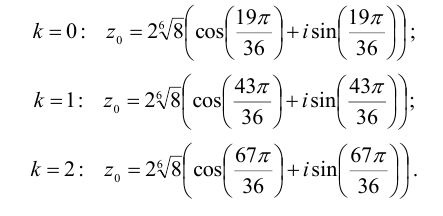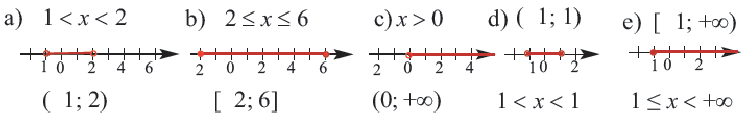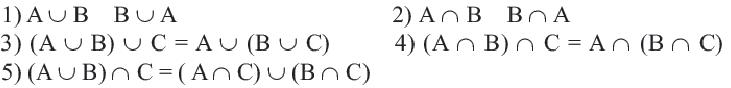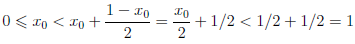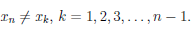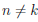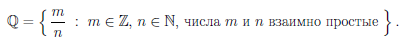Непустым множеством является множество всех рациональных корней уравнения

Нахождение рациональных корней

Содержание:

Теорема о рациональных корнях

Если для многочлена с целыми коэффициентами существует рациональный корень, то этот корень имеет вид

Доказательство:

Пусть несократимая дробь является корнем многочлена с целыми коэффициентами:

Умножим обе части равенства на :

Так как в последнем равенстве каждый член, кроме члена , содержит множитель и каждый член, кроме члена , содержит множитель , то коэффициент должен делится на , а коэффициент должен делится на .

Задача пример №8

Найдите рациональные корни многочлена .

Решение:

свободный член 6, старший коэффициент 2.

Для , запишем все возможные числа вида

, т.е. одним из множителей является двучлен . Другие множители найдем, используя синтетическое деление:

Так как, , получим, что являются корнями многочлена.

Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.

Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.

Задача пример №9

Найдите корни многочлена .

Решение:

по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.

Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.

Так как , то, решив квадратное уравнение , получим другие корни: . Значит данный многочлен третьей степени имеет три корня: —.

Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.

Например, для нахождения корней многочлена надо умножить все члены уравнения на 12, а затем решить полученное уравнение .

Для нахождения рациональных корней выполните следующие действия:

1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.

2. Из этих чисел выбирается число (обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен , на который многочлен делится без остатка.

3. Для данного многочлена при помощи синтетического деления на двучлен определяется другой множитель.

4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.

5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена могут являться числа ±1.

Проверим: ; . Значит, многочленах не имеет рациональных корней.

Исследование:

1) Перепишите примеры в тетрадь и проведите обсуждение.

a) Многочлен первой степени имеет один корень:

b) Многочлен второй степени имеет два корня: , ;

c) Многочлен третьей степени имеет три корня:

d) Многочлен четвертой степени имеет четыре корня:

e) Принимая во внимание, что уравнение имеет кратные корни, получим 5 корней:

2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид .

3) Равна ли степень произвольного многочлена количеству его корней?

Покажем на примере, что многочлен n-ой степени имеет n корней.

Задача пример №10

Найдите все корни многочлена .

Решение:

рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

.

Значит, является корнем данного многочлена . Другие корни найдем синтетическим делением.

В выражении для множителя вновь применим теорему о рациональных корнях и синтетическое деление. Тогда ; . Решим уравнение ; ; (корень кратности 2); ;

Корни:

Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Числовые множества — определение и вычисление с примерами решения

Содержание:

Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление.

Наиболее распространенные числовые множества:

• N — множество натуральных чисел;
• Z — множество целых чисел;
• Q — множество рациональных или дробных чисел;
• R — множество действительных чисел.

Основные понятия о числовых множествах

Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом.

Некоторое непустое подмножество А множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число К такое, что

Всякое число К с указанным свойством называют верхней (нижней) гранью множества А.

Непустое подмножество А множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество А называется неограниченным сверху (снизу), если какое бы число К мы бы не предложили в качестве верхней (нижней) границы множества А, всегда найдется элемент этого множества, который будет больше (меньше) К.

Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Наименьшую из верхних граней непустого подмножества множества действительных чисел А называют точной верхней гранью этого множества и обозначают sup А. Наибольшую из нижних граней непустого подмножества множества действительных чисел А называют точной нижней гранью этого множества и обозначают inf А. Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).

Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.

Граничной точкой множества называется точка, у которой в любом содержащем ее открытом промежутке найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Сама граничная точка может, как принадлежать множеству, так и не принадлежать ему.

Граница множества — совокупность граничных точек множества:

• N (множество натуральных чисел) ограниченно снизу (например, числом -2) и не ограничено сверху;
• R (множество действительных чисел) неограничено;
• множество отрицательных чисел неограничено снизу и ограничено сверху.

Соединения. Бином Ньютона

Рассмотрим совокупность n различных элементов. Произвольная упорядоченная выборка из этих элементов: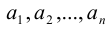

называется соединением. Эта выборка может быть как без повторений, так и с повторениями.

Раздел элементарной математики, в котором для конечных множеств рассматриваются различные соединения элементов, такие, как сочетания, размещения, перестановки, а также все виды соединений с повторениями называется комбинаторика. Задачи комбинаторики впервые рассматривались в связи с возникновением теории вероятностей, где к задачам комбинаторики приводит подсчет вероятностей на основе гипотезы равновозможных элементарных событий.

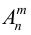
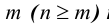
Размещениями из п элементов поназывают их соединения, каждое из которых содержит ровно m различных элементов (выбранных из данных элементов) и которые отличаются либо сами элементами, либо порядком элементов.

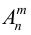
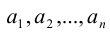
Определим число размещений из n элементов по m.

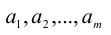
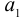
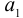
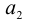
Будем строить произвольное соединениепоследовательно. Сначала определим его первый элемент . Очевидно, что из данной совокупности n элементов его можно выбрать n различными способами. После выбора первого элемента , для второго элемента остается n -1 способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Для m элементов формула приобретает вид:

Соединения из n элементов, каждое из которых содержит все n элементов, и которые отличаются лишь порядком элементов, называются перестановками .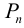

Перестановки являются частным случаем размещений. Так как каждая перестановка содержит все n элементов множества, то различные перестановки отличаются друг от друга только порядком элементов.

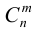
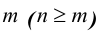
Сочетаниями из n элементов по называют такие их соединения, каждое из которых содержит ровно m данных элементов, и которые отличаются хотя бы одним элементом.

Рассмотрим все допустимые сочетания элементов .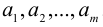

Делая в каждом из них m! возможных перестановок их элементов, очевидно, получим все размещения из n элементов по m:

Числа 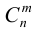являются коэффициентами в формуле бинома Ньютона:

Свойства 1 и 2 очевидно следуют из определения 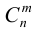, свойства 3 и 4 доказываются с помощью бинома Ньютона, полагая для свойства 3 что а = 1 и b = 1, а для свойства 4 что a = 1 и b = -1. Свойство 5 можно проверить следующим образом:

Это свойство позволяет последовательно вычислять биномиальные коэффициенты С»‘ с помощью так называемого треугольника Паскаля:

Здесь каждое число, кроме крайних единиц, является суммой двух вышерасположенных.

Комплексные числа

В арифметике и алгебре рассматривают различные действия над числами: арифметические (сложение, вычитание, умножение, деление), возведение в степень, извлечение корня и т.д. Только два действия — сложение и умножение — безусловно, выполнимы в области натуральных чисел: сумма и произведение натуральных чисел — также натуральные числа. Однако в области арифметики натуральных чисел уже вычитание не всегда выполнимо — для возможности образования разности двух натуральных чисел множество N нужно дополнить до множества целых чисел Z, введя в него ноль и целые отрицательные числа. Такие операции как деление и извлечение корня становятся выполнимыми только после расширения рассматриваемой числовой области: множество целых чисел должно быть, соответственно, дополнено вначале до множества Q за счет введения рациональных чисел, а потом и до множества действительных чисел R за счет введения иррациональных чисел.

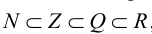
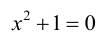
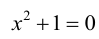
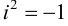
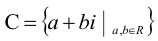
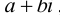
Этот процесс можно схематически изобразить цепочкой , где N, Z, Q, R обозначают соответственно множества натуральных, целых, рациональных и действительных чисел. Причем каждая последующая числовая система сохраняет все основные свойства предыдущей и обладает рядом новых полезных свойств. Так, в N можно только складывать и умножать, в Z можно уже вычитать, в Q — делить. Во множестве R действительных чисел можно извлекать корни любой степени из положительных чисел, хотя в Q даже число не имеет смысла. Но и в множестве действительных чисел R такое простое уравнение не имеет решений. Так как многие задачи практики приводят к алгебраическим уравнениям, требуется построить новое множество, содержащее множество действительных чисел и решение любого алгебраического уравнения. Символом i, который называется мнимой единицей, обозначим корень уравнения, или . Множество, которое представляет собой множество всех двучленов вида , называется множеством комплексных чисел.

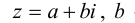
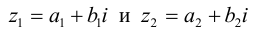
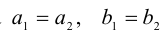
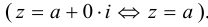
Действительное число а называется действительной частью комплексного числа — мнимой частью или коэффициентом при мнимой единице. Два комплексных числа будут равны тогда и только тогда, когда При этом действительные числа рассматриваются как частный случай комплексных чисел, мнимая часть которых равна нулю . Комплексное число равно нулю тогда и только тогда, когда равны нулю его действительная и мнимая части.

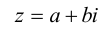
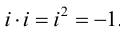
Операции сложения, вычитания и умножения над числами вида производятся по обычным правилам алгебры с единственным дополнительным условием: .

Операции над комплексными числами

Алгебраическую операцию сложения на множестве С можно задать следующим образом:

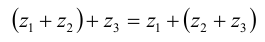
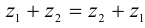
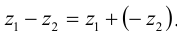
Сложение комплексных чисел ассоциативно, т.е. и коммутативно, т.е. . Сумма чисел (a + bi)+(—a—bi) = 0, поэтому число -a-bi является противоположным числу a + bi, тем самым определена операция вычитания .

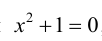
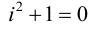
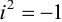
Учитывая, что через i обозначен корень уравнения т.е. или , можно определить умножение комплексных чисел:

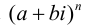
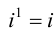
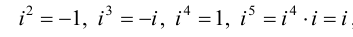
Умножение также ассоциативно и коммутативно. Произведение нескольких сомножителей вычисляется как последовательное умножение. Натуральная степень комплексного числа может быть найдена при помощи формулы бинома Ньютона. Поскольку , , при возведении i в любую натуральную степень n, надо найти остаток от деления n на 4 и возвести i в степень, равную этому остатку.

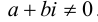
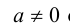
Чтобы определить деление комплексных чисел, нужно определить число обратное числу . Для действительного числа обратным будет число

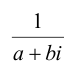
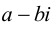
Выражение запишем в стандартной форме. Для этого умножим числитель и знаменатель на комплексное число :

Значит, для любого ненулевого комплексного числа существует обратное. Таким образом, операция деления определена как произведение делимого на число, обратное делителю.

Множество комплексных чисел является расширением множества действительных чисел, любое действительное число а можно записать в виде .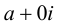

Число а-b называется сопряженным числу z = a + bi и обозначается .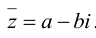

Сумма и произведение сопряженных чисел являются числами действительными:

Число 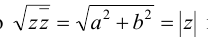называется модулем или абсолютной величиной комплексного числа a + bi. Очевидно, что

Свойства сопряжения:

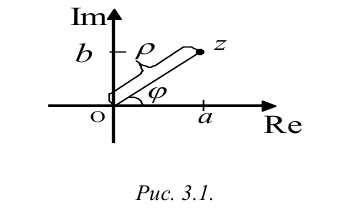
Каждому комплексному числу z = a + bi поставим в соответствие точку Z плоскости, координатами которой в прямоугольной системе координат являются числа а и b.

Тогда каждой точке Z(a,b) плоскости будет соответствовать единственное комплексное число a + bi. В результате получается взаимно однозначное соответствие между множеством комплексных чисел С и множеством точек плоскости, которое позволяет отождествить произвольное комплексное число a + bi с точкой плоскости, имеющей в выбранной системе координат координаты (a,b). При этом точки горизонтальной координатной оси Re изображают действительные числа и поэтому эту ось называют действительной осью, а по вертикальной оси Im откладываются мнимые части комплексных чисел, поэтому вертикальная ось Im называется мнимой осью.

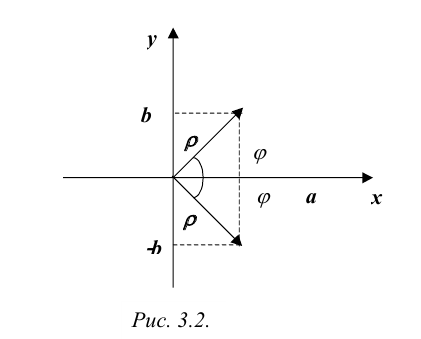
Расстояние от точки Z до начала координат есть действительное неотрицательное число р, которое называется модулем комплексного числа z = a + bi и обозначается \z\ = p. Угол между положительным направлением действительной оси и радиус-вектором точки z называется аргументом z и обозначается arg z. Для числа 0 аргумент не определен, для остальных комплексных чисел аргумент определяется с точностью до целых кратных 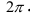, при этом положительные углы отсчитываются против часовой стрелки.

Пусть z = a + bi. Из рис. 3.1 ясно, что модуль числа z находится

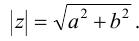
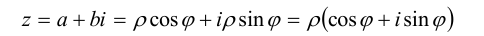
по формуле Аргумент числа z определяется из равенств

(3.1)

Запись числа z в виде (3.1) называется тригонометрической формой комплексного числа.

Если воспользоваться формулой Эйлера,

то от тригонометрической формы записи комплексного числа (3.2) несложно перейти к его показательной форме записи:

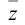
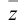
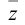
Пусть z и — сопряженные числа. Если z = а + bi, то = a- bi. Геометрически z и являются точками, симметричными относительно действительной оси (рис. 3.2). Отсюда вытекают равенства

Перемножать и делить комплексные числа удобнее, если они представлены в тригонометрической форме:

В показательной форме:

При умножении комплексных чисел их аргументы складываются, а модули перемножаются. Это правило верно для любого числа сомножителей. Аналогично,

(3 4)

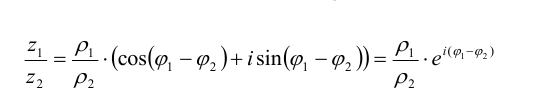
При вsполнении деления комплексных чисел в тригонометрической форме их аргументы вычитаются, а модули нужно разделить.

Формула Муавра. Извлечение корня из комплексного числа

Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую формулой Муавра:

Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.

Перейдем к процедуре извлечения корней. Известно, что во множестве действительных чисел не из всякого действительного числа можно извлечь корень. Например, 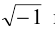не существует. В множестве комплексных чисел дело обстоит иначе.

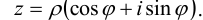
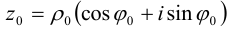
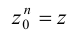
Пусть . Комплексное число

называется корнем n-й степени из z, если

, т.е.:

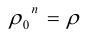
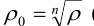
Модуль комплексного числа определяется однозначно, поэтому или (здесь имеется в виду арифметический корень).

Аргумент комплексного числа определяется с точностью до

. Следовательно,

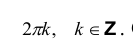
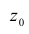
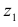
Таким образом, комплексное число , которое является корнем n -й степени из , имеет вид:

Придавая А- различные значения, мы не всегда будем получать различные корни. Действительно, k можно записать в виде k = nq + t, где 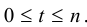. Тогда:

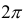
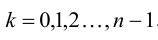
Т.е. значение аргумента при данном к отличается от значения аргумента при k = t на число, кратное . Следовательно, в формуле (2) можно ограничится лишь значениями . При таких значениях к получаются различные корни, так как разность между их аргументами по абсолютной величине меньше .

Итак, для каждого ненулевого числа z существует ровно n корней n -й степени из z.

Пример:

Вычислить

Решение:

Представим число, стоящее под знаком корня, в тригонометрической форме:

Извлечем далее корень третьей степени из этого комплексного числа:

Отсюда полагая, что k = 0,1,2, получим:

Числовые множества и форма их представления

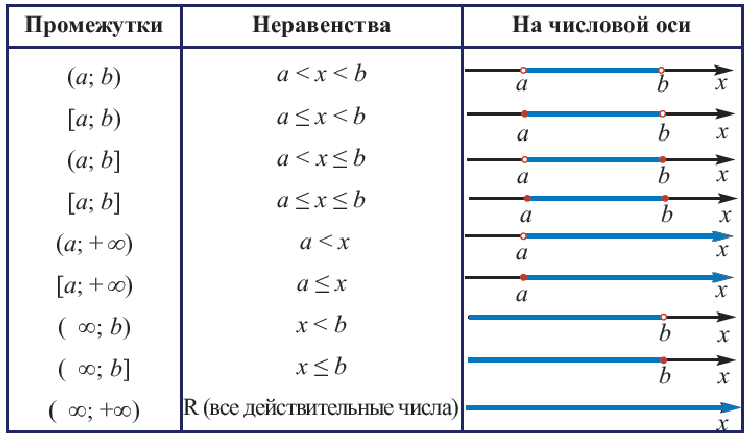
Множество, элементы которого являются действительными числами называется числовым множеством. В основном, числовые множества задаются в виде неравенств или в виде промежутков. Множество всех действительных чисел обозначается как

Пример:

Изобразите на координатой прямой множество чисел, удовлетворяющих неравенству. Запишите в виде промежутков.

Свойства объединения и пересечения числовых множеств

Некоторые свойства пересечения и объединения множеств подобны переместительным, сочетательным и распределительным свойствам сложения и умножения чисел.

Верные для множеств равенства, соответствующие свойствам 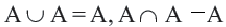для чисел не всегда верны.

Пример:

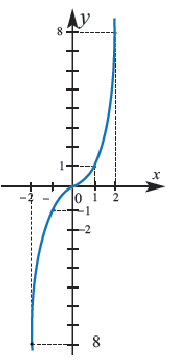
Графиком функции 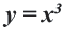называется кубическая парабола.

Если , то (куб положительного числа — положительное число), если , то (куб отрицательного числа — отрицательное число), если , то .

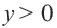
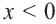
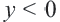
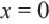
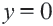
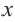
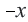
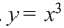
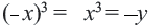
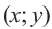
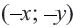
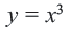
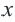
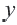
Поэтому график функции проходит через начало координат и расположен в I и III четвертях. Если значение заменить его противоположным значением , тогда функция будет принимать противоположное значение: т.к. , то . Значит, каждой точке графика функции соответствует точка , симметричная относительно начала координат на данном графике. Таким образом, график функции симметричен относительно начало координат. По графику видно, что число , куб которого равен данному числу — единственное.

Свойства числовых множеств

Ограниченные числовые множества

Определение 1.26. Пусть X — непустое числовое множество. Множество X называется ограниченным сверху (снизу), если существует такое число a, что x 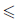a (x a) для любого элемента x ∈ X . При этом число a называется верхней (нижней) границей множества X . Множество, ограниченное снизу и сверху называют ограниченным.

С помощью логических символов ограниченность сверху множества X записывают следующим образом:

∃ a ∈ 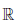: x a, ∀x ∈ X.

Учитывая свойства модуля числа, можно дать следующее равносильное определение граниченного множества.

Определение 1.27. Непустое числовое множество X называют ограниченным, если существует такое положительное число M, что

|x| M, ∀x ∈ X.

Определение 1.28. Элемент a из числового множества X называют максимальным (минимальным) элементом в X, если x a (соответственно, x > a) для любого x из X, и пишут: a = max X (соответственно, a = min X).

В силу аксиомы порядка (3.b) легко показать, что если множество X в имеет максимальный (минимальный) элемент, то он единственен.

Отметим, что если числовое множество X имеет максимальный (минимальный) элемент a, то оно ограничено сверху (снизу) и число a является верхней (нижней) границей множества X. Однако не всякое ограниченное сверху (снизу) числовое множество имеет максимальный (минимальный) элемент.

Пример 1.5. Покажем, что множество X = [0, 1) не имеет максимального элемента.
Заметим, что множество X ограничено сверху и 1 — одна из его верхних границ. Пусть x₀ — любой элемент из X . Тогда 0 x0 1 и

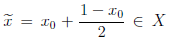
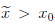
Следовательно, и . Последнее означает, что x₀ не является максимальным элементом множества X. Но x₀ — произвольный элемент X , поэтому множество X не имеет максимального элемента.

Замечание. Любое числовое множество, содержащее конечное число элементов, имеет максимальный и минимальный элементы.

Теорема 1.2 (принцип полноты Вейерштрасса). Если непустое числовое множество ограничено сверху (снизу), то существует число, которое является наименьшей верхней (соответственно, наибольшей нижней) границей этого множества, и это число единственно.

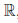
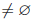
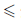
Пусть X ⊂, X и ограничено сверху. Обозначим через Y множество верхних границ множества X, то есть Y = | x y, ∀x ∈ X>. По условию Y и 6 y, ∀ x ∈ X, ∀ y ∈ Y . По аксиоме полноты

∃ c ∈ 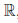: x c y, ∀x ∈ X, ∀y ∈ Y.

Поскольку x c, ∀x ∈ X , то c ∈ Y . Но c y, ∀y ∈ Y , значит c — наименьшая верхняя граница множества X , то есть минимальный элемент множества Y. Поэтому он единственен.

Определение 1.29. Пусть X — непустое ограниченное сверху числовое множество. Наименьшую из верхних границ множества X называют точной верхней границей или верхней гранью множества X и обозначают sup X (читают «супремум X») или sup x.

Итак, sup X = min| x c, ∀x ∈ X> и потому определение 1.29 равносильно следующему.

Определение 1.30. Пусть X — непустое ограниченное сверху числовое множество. Число a называют точной верхней границей множества X , если выполнены два условия:

1. x a, ∀x ∈ X ;

2. ∀ε > 0 ∃ xε ∈ X : xε > a — ε.

Условия 1-2 являются характеристическими свойствами sup X. Первое означает, что a — верхняя граница множества X , а второе — что любое число b, меньшее чем a, уже не является верхней границей множества X .

С учетом определения 1.29 принцип полноты множества R в смысле Вейер-штрасса формулируется следующим образом:

Теорема 1.3. Непустое ограниченное сверху числовое множество имеет, притом единственную, точную верхнюю границу.

Аналогично вводится понятие точной нижней границы множества.

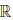
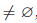
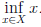
Определение 1.31. Пусть X ⊂ , X , ограничено снизу. Наибольшую из его нижних границ называют точной нижней границей или нижней гранью множества X и обозначают inf X (читают «инфимум X») или .

Характеристическими свойствами a = inf X, a ∈ 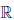, являются:

1) a x, ∀x ∈ X ; 2) ∀ε > 0 ∃ xε ∈ X : xε a + ε.

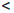
Лемма 1.2. Если числовое множество X имеет максимальный (минимальный) элемент a, то a = sup X (соответственно a = inf X).

Пусть a = max X . Тогда a ∈ X и x a, ∀x ∈ X . Поэтому a — верхняя граница множества X и ∀ε > 0, если положить xε = a ∈ X , имеем:

∃ xε = a ∈ X : xε > a — ε.

Следовательно, по определению 1.30 a = sup X.

Пример 1.6. Найти sup X, если X = [0, 1).

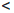
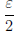
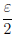
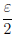
Так как x 1, ∀x ∈ X , то 1 — верхняя граница множества X . Пусть ε — произвольное положительное число, меньшее 1. Число 1 — принадлежит множеству X. Поскольку 1- > 1 — ε, то можно положить xε = 1- . Поэтому 1=supX.

Неограниченные числовые множества

Определение 1.32. Если непустое числовое множество не является ограниченным сверху (снизу), то его называют неограниченным сверху (снизу).В символьной форме это определение принимает вид:

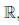
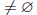
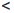
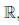
X ⊂ , X не ограничено сверху ⇒ ∀a ∈ ∃ x ∈ X : x>a.

В случае, если числовое множество X не ограничено сверху считают, что его точная верхняя граница равна +∞.

Если же X не ограничено снизу, то считают, что inf X = -∞.

Из сказанного и теоремы 1.2 вытекает следующий результат.

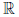
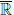
Теорема 1.4 (существования точных границ). Каждое непустое множество X из имеет в точные верхнюю и нижнюю границы; sup X — число, если X ограничено сверху, sup X = +∞, если X не ограничено сверху; inf X — число, если X ограничено снизу и inf X = -∞, если X не ограничено снизу.

Теорема 1.5. Непустое ограниченное сверху (снизу) подмножество множества Z имеет максимальный (минимальный) элемент.

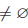
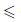
Пусть X ⊂ Z, X 6, X — ограниченное сверху множество. По теореме 1.2 о существовании точных границ числового множество имеется число C такое, что C = sup X. Поэтому для любого ε > 0 и, в частности, ε = 1 найдется такой элемент xε = n₀ ∈ X, что n₀ > C- 1, то есть n₀ C n₀+1. Поскольку между n₀ и n₀ + 1 нет целых чисел, то ∀m ∈ X m n₀ и, следовательно, n₀ = max X .

Теорема 1.6. Бесконечное подмножество натуральных чисел не ограничено сверху.

Пусть X — бесконечное подмножество множества 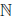. Предположим, что оно ограничено сверху. Так как X ⊂ Z, то по теореме 1.5 множество X имеет максимальный элемент n₀ . Тогда X имеет не более n₀ элементов, что противоречит условию.

Теорема 1.7 (принцип Архимеда). Для любого числа a и любого положительного числа b найдется единственное целое число n₀ такое, что (n₀-1)b a n₀b.

Так как ⊂ , то множество не ограничено сверху, поэтому существует число n ∈ такое, что n > a/b. Пусть Y = a/b>. Множество Y является непустым ограниченным снизу. По теореме 1.5 оно имеет минимальный элемент. Пусть n₀ = min Y . Тогда n₀ — 1 ∈/ Y и n₀ —.

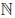
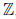
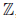
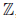
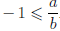
Следовательно, 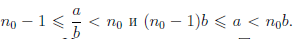Поскольку число n₀ — минимальный элемент Y , то оно единственно.

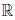
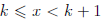
Следствие 1. Для любого числа x ∈ существует единственное число k ∈ такое, что (достаточно в теореме положить b = 1). Такое число k называют целой частью числа x и обозначают через [x] или E (x).

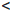
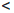
Следствие 2. Для любого положительного числа ε существует натуральное число n такое, что 0 1/n ε.

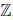
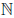
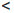
Пусть ε — положительное число. По принципу Архимеда найдется такое n ∈ , что n > 1∕ε. Поскольку ε > 0, то n ∈ и 0 1/n ε.

Теорема 1.8 (о плотности в ). Для любых чисел a, b ∈ , a b, найдется рациональное число r такое, что a r b.

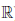
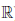
Число b — a положительно. По следствию 2 принципа Архимеда подберем натуральное число n₀ такое, что 0 1∕n₀ b—a. Далее, по принципу Архимеда по числу a и 1∕n₀ > 0 найдется m0 ∈ :

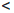
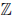
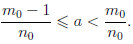
Докажем, что рациональное число m₀∕n₀ — искомое. Действительно,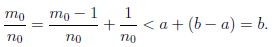

Отсюда, a m_o∕n_o b.

Счетные и несчетные множества

При изучении множеств приходится по некоторым правилам сравнивать их между собой по запасу элементов. Изложим одно такое правило.

Пусть n — натуральное число, а N_n = : k n>. Множество X называют конечным, если существует такое n ∈ , что между множествами X и N_n можно установить биективное отображение, в противном случае множество X называют бесконечным.

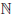
Определение 1.33. Бесконечное множество X называют счетным, если существует биективное отображение f : 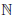→ X . Если бесконечное множество X не является счетным, его называют несчетным.

Иными словами, счетное множество — это такое бесконечное множество, элементы которого можно занумеровать: a₁, a₂, . . . , a_n, . . . , n ∈ .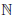

Пример 1.7. Множество X натуральных четных чисел счетно, поскольку функция f : 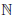→ X, f(n) = 2n, является биекцией.

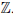
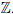
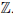
Пример 1.8. Множество целых чисел счетно. В этом случае биективное отображение f : N → , f(n) = (-1)n-1 [n/2], позволяет пронумеровать элементы множества следующим образом:

0, -1, 1, -2, 2, -3, . . . , -n, n, . . . , n ∈ .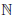

Теорема 1.9. Любое бесконечное множество содержит счетное подмножество.

Пусть X — бесконечное множество, а x₁ — произвольный элемент из X . Заметим, что множество 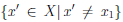бесконечно. Зафиксируем любой элемент этого множества и обозначим его x₂. Продолжая этот процесс, на n-ом шаге выделим элемент x_n ∈ X такой, что

В результате получим множество Y = 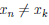>, которое является счетным, так как при

Теорема 1.10. Объединение конечной или счетной совокупности счетных множеств есть счетное множество.

Пусть множество A является объединением счетной совокупности счетных множеств A₁ , A₂, Поскольку множества A_k, k ∈ 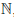, являются счетными, то их можно представить в виде:

Пронумеруем элементы множества A следующим образом:

Если у множеств A_i и A_j , 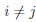, окажутся одинаковые элементы, то их посчитаем один раз. Поскольку A = k : k ∈ > и a_i a_j , если i j, то множество A — счетно.

Следствие. Множество рациональных чисел счетно.

Множество рациональных чисел определяется следующим образом:

Расположим рациональные числа в таблицу. Сначала в первую строку поместим все целые числа в порядке не убывания их абсолютных величин и так, что за каждым натуральным числом следует ему противоположное:

Во вторую строку поместим все несократимые рациональные числа со знаменателем 2 в порядке не убывания их абсолютных величин, причем вслед за каждым положительным числом следует ему противоположное:

Аналогично, в n-ую строку выпишем все несократимые рациональные числа со знаменателем n, упорядоченные по абсолютной величине и вслед за каждым положительным числом вписано ему противоположное. В результате получим таблицу всех рациональных чисел, состоящую из счетного множества строк, каждая из которых содержит счетное множество элементов. При этом среди выписанных элементов нет одинаковых. По теореме 8 множество счетно.

Определение 1.34. Конечные и счетные множества называют не более чем счетными.

• Вектор — определение и основные понятия
• Прямая — понятие, виды и её свойства
• Плоскость — определение, виды и правила
• Кривые второго порядка
• Степень с действительным показателем
• Логарифм — формулы, свойства и примеры
• Корень из числа — нахождение и вычисление
• Теория множеств — виды, операции и примеры

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

. Равенство множеств. Подмножество. Универсальное множество. Дополнение множества

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ОСНОВНЫЕ ДАННЫЕ О РАБОТЕ

В обычной речи мы часто употребляем слово “множество”: множество людей, множество книг, множество законов, множество денег и т.д.

В математике множеством называют совокупность, набор каких-либо предметов (объектов). Это не есть точное математическое определение. Так же, как и понятия точки, числа и т.д., понятие множества является одним из тех первоначальных, наиболее общих понятий, которые приходится принимать без определения.

Предметы, составляющие множество, называются его элементами. То, что элемент а входит в множество А, записывается так: а  А (читается: а есть элемент множества А, или: а принадлежит множеству А). Запись а  А означает, что элемент а не принадлежит множеству А. Термин “множество” употребля­ется независимо от того, много или мало в этом множестве элементов. Мно­жество, не содержащее ни одного элемента, называется пустым и обозначается символом  .

Примерами пустых множеств могут служить:

а) множество действительных чисел, являющихся корнями уравнения x 2 + 1 = 0;

б) множество треугольников, сумма углов которых отлична от 180°;

в) множество решений системы уравнений

.

В каком случае можно считать, что множество задано? Иногда можно задать множество, перечислив все его элементы. Например, множество учеников в классе задается перечислением фамилий в классном журнале. Это нетрудно сделать, так как такое множество содержит конечное число элементов. Однако не всякое конечное множество можно задать перечислением. Множества слонов на нашей планете или рыб в океане тоже конечные, но попробуйте их перечислить
(или пересчитать!)! Тем более нельзя перечислить все элементы бесконечного множества. Так, множество всех цифр конечное и их легко перечислить: А=<0,1,2,3,4,5,6,7,8,9>. А вот множество всех целых чисел, составленных из этих цифр, бесконечное и их уже не перечислишь. В таких случаях множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называется характерис-тическим свойством множества. Одно и то же множество может быть задано различными характеристическими свойствами. Например, множество <2,4>может быть задано как:

а) множество четных чисел, удовлетворяющих неравенству 1

б) множество корней квадратного уравнения .

Записывается это таким образом: А= или А=< x : x 2 – 6 x + 8 = 0>.

В геометрии множество точек, обладающих данным характеристическим свойством, часто называют геометрическим местом точек с данным свойством. Биссектриса угла есть геометрическое место точек плоскости, лежащих внутри этого угла и равноудаленных от его сторон. Окружность — геометрическое место точек плоскости, расстояние которых от данной точки О (центра окружности) равно числу R (радиусу окружности).

1.2. Равенство множеств. Подмножество. Универсальное множество. Дополнение множества

Если А и В два множества, то запись А=В означает, что они состоят из одних и тех же элементов. Если каждый элемент множества А является в то же время элементом множества В, то говорят, что А — подмножество в В, и пишут А  В. Каждое непустое множество имеет по крайней мере два подмножества: пустое множество  и само множество А.

Приведем примеры подмножеств:

а) множество учеников 10-го класса данной школы есть подмножество множества всех учеников этой школы;

б) множество жителей Москвы является подмножеством множества жителей России;

в) множество всех квадратов есть подмножество множества всех прямоугольников;

г) множество Z всех целых чисел есть подмножество множества Q всех рациональных чисел.

Если одновременно с отношением А  В имеет место отношение В  А, то А=В. То есть, если одновременно А есть подмножество В и В есть подмножество А, то такие два множества равны.

Введенные в этом параграфе отношения наглядно иллюстрируются с помощью так называемых диаграмм Венна. Диаграмма Венна — это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи — элементы, не принадлежащие этому множеству. Например, диаграмма множества В= <*,+,  >изображена на рис. 1.

Отношение А  В изображено с помощью диаграмм на рис. 2 а, б.

Пусть нам дано какое-либо множество Е. Мы будем рассматривать всевозможные подмножества данного множества Е. Исходное множество Е в таком случае называют универсальным множеством. В качестве примера возьмем множество книг. В это множество входят подмножества научных, художественных книг, книг по искусству; среди научных книг есть подмножества книг по математике, химии, биологии и т.д. Множество всех книг — это универсальное множество, содержащее в себе различные подмножества книг. Сколько этих подмножеств? — Очень много! — скажете Вы. — Тогда давайте рассмотрим пример попроще. Пусть универсальное множество Е состоит из трех элементов: . Перечислим все подмножества
Е: , , , , , , , <  >. Их всего 2 3 = 8 подмножеств. Можно доказать, что если универсальное множество Е состоит из n элементов, то число всех подмножеств множества Е равно 2 n .

Пусть множество А есть некоторое подмножество универсального множества Е. Тогда множество , состоящее из всех элементов множества Е, не принадлежащих множеству А, называется дополнением множества А. Например, если А — множество всех девочек в классе, то дополнением является множество всех мальчиков того же класса. Дополнением множества всех квадратов в множестве всех прямоугольников является множество всех прямоугольников с неравными сторонами. Если Е=<целые числа>, А=<четные числа>, то =<нечетные числа>.

1.3. Операции над множествами: объединение, пересечение, разность

1. Объединением С двух множеств А и В называется множество, состоящее из всех элементов, принадлежащих множеству А или множеству В. Обозначают это так: С=А  В. Союз “или” здесь неразделительный, то есть не исключается возможность одновременной принадлежности некоторых элементов и множеству А, и множеству В. При этом такие элементы зачисляются в объединение С только один раз. Иными словами, в объединение входят все элементы, принадлежащие хотя бы одному из множеств. Объединение часто называется суммой множеств. Объединение трех и более множеств определяется аналогично. На рис. 3 и 4 заштрихованные множества — это объединения двух и трех множеств, соответственно.

Примеры. а) Обозначим через А множество точек круга R₁, а через B — множество точек круга R₂ (рис. 5). Тогда их объединением будет множество точек фигуры, ограниченной на рисунке 5 жирной линией.

б) Обозначим через А множество успевающих учеников в классе, через В множество девочек в этом классе и через С множество неуспевающих мальчиков. Тогда А  В  С является множеством всех учащихся этого класса. Множества А и В имеют общие элементы — успевающих девочек.

в) Обозначим через А множество целых чисел, через В множество четных чисел. Тогда А  В есть множество А, то есть А  В=А.

2. Пересечением С двух множеств А и В называется множество, состоящее из элементов, принадлежащих множеству А и множеству В одновременно. Обозначают это так: С=А  В. Иными словами, пересечение образовано всеми общими элементами данных множеств. Аналогично определяется пересечение трех и более множеств. На рис. 6 и 7 заштрихованные множества —
это пересечения двух и трех множеств, соответственно.

Примеры. а) Термин “пересечение” по существу геометрического происхождения. Пересечением прямой и плоскости, если прямая не параллельна плоскости, является их единственная общая точка. Если прямая и плоскость параллельны, то пересечение этих множеств пусто. Если же прямая лежит на плоскости, то их пересечение совпадает с множеством точек этой прямой.

б) Пусть А — множество мальчиков, обучающихся в данной школе, а В — множество всех учеников из 10-го класса. Тогда пересечение А  В — множество мальчиков, которые учатся в этом классе.

в) С пересечением множеств, по сути, мы уже имели дело и в арифметике. Пусть А — множество натуральных делителей числа 72: А=<1,2,3,4,6,8,9, 12,18,24,36,72>, а В — множество натуральных делителей числа 54: В=<1,2,3,6,9,18,27,54>. Тогда множество А  В=<1,2,3,6,9,18>. Эти числа являются общими делителями для 72 и 54. Наибольший элемент множества А  В, то есть 18, называется наибольшим общим делителем чисел 54 и 72.

Множество делителей числа 72 конечно. А множество кратных этого числа бесконечно: С=<72,144,216. 72n. >.

Бесконечно и множество кратных числа 54: D=<54,108,162,216. 54m. >.

Пересечением этих множеств является множество общих кратных для чисел 72 и 54: С  D=<216,432. >.

Наименьшее число в С  D, то есть 216, называется наименьшим общим кратным для 72 и 54.

3. Разностью С двух множеств А и В называется множество, состоящее из всех элементов А, не входящих в В. Обозначают это так: С=А\В. Таким образом, из множества А достаточно удалить общие элементы множеств А и В, то есть все элементы множества А  В, чтобы получить разность А\В. На рис. 8, 9 и 10 для разных случаев заштрихованные множества — это разность А\В двух множеств.

Рис. 8 Рис. 9 Рис. 10

Примеры. а) Если А — множество всех учащихся 8-го класса данной школы, а В — множество всех девочек, которые учатся в школе, то А\В — множество всех мальчиков, которые обучаются в этом 8-ом классе.

б) Пусть А — множество натуральных четных чисел, а В — множество всех целых чисел, делящихся на 4. Тогда А\В — множество всех четных натуральных чисел, которые не делятся на 4.

в) Разностью множества четных чисел и множества целых чисел является пустое множество.

1.4. Основные законы операций над множествами

Некоторые свойства объединения и пересечения множеств очень похожи на свойства хорошо известных алгебраических операций сложения и умножения. Вместе с тем многие свойства введенных операций над множествами отличаются от свойств алгебраических операций. Приведем здесь основные свойства:

1. А  В=В  А и А  В=В  А — переместительные законы объедине­ния и пересечения множеств.

2. (А  В)  С=А  (В  С) и (А  В)  С=А  (В  С) — сочетательные законы объединения и пересе-чения множеств.

3. А  =А, А  =  , А\  =А, А\А=  .

Здесь роль пустого множества аналогична роли числа 0 в алгебре. Однако свойство  \А=  уже не имеет аналога в алгебре.

4. A  E = A .

5. А  (В  С)=(А  В)  (А  С) — распределительный закон пересече­ния относительно объединения; А  (В  С)=(А  В)  (А  С) — распределительный закон объедине­ния относительно пересечения.

Первый распределительный закон аналогичен соответствую­щему распределительному закону в алгебре. А вот второй закон никакого аналога в алгебре не имеет.

Свойства, сформулированные в п.п.1-4, очевидны и не нуждаются в доказательстве. Распределительные законы в п.5 уже сложнее. Однако вместо того, чтобы их строго доказывать, лучше попытаться их понять, пользуясь диаграммами Венна.

На рис. 11 заштриховано пересечение множества А с множеством В  С, а на рис. 12 — объединение двух пересечений А  В и А  С. Эти рисунки делают первый распределительный закон вполне понятным.

На рис. 13 заштриховано объединение множеств А и В  С. На рис. 14 штриховкой с наклоном вправо показано множество А  В, а штриховкой с наклоном влево — множество А  С.
В результате то множество, на котором штриховки наложились друг на друга, представляет собой пересечение множеств А  В и А  С. Эти рисунки делают и второй распределительный закон также понятным.

1.5. Числовые множества. Множества точек на прямой,
задаваемые алгебраическими уравнениями и неравенствами

Множества могут состоять из объектов самой различной природы. Их элементами могут быть буквы, атомы, книги, люди и т.д. Для математики особо важную роль играют множества, составленные из “математических” объектов — чисел, точек, геометрических фигур и т.п. Примерами числовых множеств являются:

а) множество всех действительных чисел R;

б) множество всех рациональных чисел Q;

в) множество всех натуральных чисел N;

г) множество всех чисел вида , где n принимает все натуральные значения.

1. Интервалы. Если a и b два действительных числа и аоткрытым интервалом (числовым промежутком) и обозначается (a,b). Открытый интервал не имеет ни наименьшего, ни наибольшего числа: какое бы число x  (a,b) мы не взяли, обязательно на этом интервале найдутся такие и , что > x и x . Множество всех точек любого интервала является бесконечным.

Заштрихованная часть числовой прямой содержит все точки, принад­лежащие соответст-вующему интервалу. Незакрашенные кружочки означают, что эти точки не принадлежат интервалу, а закрашенные, наоборот, означают, что эти точки принадлежат интервалу.

Интервал (-  ,a) (или (-  ,a]) — это множество всех чисел х, удовлетворяю­щих неравенству x a). Интервал (а,+  ) (или [a,+  )) — это множество таких чисел х, которые удовлетворяют неравенству x>a (или x  a). Интервал (-  ,+  ) — это множество R всех действительных чисел. Эти интервалы геометрически изображаются так:

Фигурирующие в этих обозначениях символы +  и —  ни в коем случае нельзя понимать как действительные числа. Наличие символа +  в обозначении интервала означает, что интервал содержит любые сколь угодно большие числа (например, интервал (а,+  ) содержит все числа, большие а). По аналогии с обычным интервалом можно записать, что интервал (а,+  ) состоит из всех чисел х — таких, что a . Но фигурирующее в этой записи неравенство x  означает лишь, что х — любое действительное число, поэтому интервал (а,+  ) задается на самом деле одним неравенством x>a.

Точно так же наличие символа —  в обозначении интервала означает, что в этот интервал входят все отрицательные числа, абсолютные величины которых могут быть сколь угодно большими. Неравенство x>-  , равно как и неравенство —   , означает, что х — произвольное действительное число.

2. Окрестность точки. Окрестностью точки x ₀ называется любой открытый интервал, содержащий эту точку (рис. 15). Открытый интервал (a,b) служит окрестностью всякой принад-лежащей ему точки.

Возьмем какое-либо положительное число  .  -окрестностью точки x ₀ называется открытый интервал с центром в точке x ₀ длиной 2  , то есть интервал ( x ₀ –  , x ₀ +  ).  -окрестность точки x ₀ изображена на рис. 16. Забегая вперед (см. п.3), скажем, что можно задать  -окрестность точки x ₀ и в виде неравенства | x – x ₀|  .

3. Множества точек, задаваемые алгебраическими уравнениями и неравенствами. С каждым уравнением связаны два числовых множества. Первое из них — область определения уравнения. Это множество состоит из всех значений x , для которых имеют смысл обе части уравнения. Второе множество — это множество его корней, то есть чисел, при подстановке которых в уравнение оно обращается в тождество.

Пример 1. Уравнение имеет своей областью определения множество [-4,+  ). Найдем его корни. Возведем обе части уравнения в квадрат:

x + 4 = (2 – x ) 2 или x 2 – 5 x = 0.

Решим полученное квадратное уравнение:

x ( x – 5) = 0 или x ₁ = 0, x ₂ = 5.

Оба числа x ₁ = 0 и x ₂ = 5 принадлежат множеству [-4,+  ), однако число x ₂ = 5 является посторонним корнем уравнения (это показывает простая проверка: ). Таким образом множество корней данного уравнения <0> [-4,+  ). На прямой эти множества изображаются так:

Пример 2. Уравнение | x | = 3 имеет своей областью определения множество (-  ,+  ). Найдем его корни. По определению абсолютной величины числа х имеем:

.

Поэтому данное уравнение можно представить в виде совокупности двух уравнений: х = 3 и
–х = 3. Откуда получим два корня x ₁ = 3, x ₂ = –3. Геометрически эти решения можно истолковать так: расстояние от x ₁ до начала отсчета О и расстояние x ₂ до начала отсчета О равны 3 (рис. 17).

В случае уравнения | x – x ₀ = a |, где a > 0, имеем два корня и . Геометрически расстояния от точки до и от точки до равны а (рис. 18).

Пример 3. Неравенство | x | x |

Пример 4. Неравенство | x | > 3 имеет своими решениями объединение двух множеств:
(-  ,-3)  (  ,+  ). Геометрически условие | x | > 3 означает, что расстояние от точки х до начала отсчета больше 3. Множество решений этого неравенства изображено на рис. 20.

В случае неравенства | x – x ₀| a , где a > 0, множество решений имеет вид ( x ₀ – a , x ₀ + a ) и является открытым интервалом длины 2а с центром в точке x ₀ (рис. 21).

Множество решений неравенства | x – x ₀| > a , где a > 0, представляет собой объединение двух множеств: (-  , x ₀ – a )  ( x ₀ + a , +  ). Эти множества изображены на рис. 22.

Объединив случаи уравнения | x – x ₀| = a и неравенства | x – x ₀| a , по­лучим множество решений неравенства | x – x ₀|  a . Аналогично получается множество решений неравенства | x – x ₀|  a .

4. Системы уравнений и неравенств с одним неизвестным.

Пример 5. Решить систему уравнений

.

Решение. Первое уравнение — квадратное, поэтому его корни вычисля­ются по формуле:

или x ₁ = 3, x ₂ = –1.

При решении второго уравнения надо указать вначале его область определения: x  3. Далее, приравняв каждый из множителей нулю и решив получившиеся уравнения, будем иметь x ₁ = 3,
x ₂ = –2. Число x ₂ = –2 не принадлежит области определения [3,+  ) и является посторонним корнем. Следовательно, система уравнений имеет единственное решение: <3>.

Пример 6. Решить систему неравенств:

.

Решение. Первое неравенство линейное и его множество решений имеет вид (-  ,2]. Второе неравенство — квадратное, его можно решить методом интервалов. Для этого разложим квадратный трехчлен в произведение:

x 2 – 5 x – 6 = ( x + 1) ( x – 6).

Далее числа x ₁ = –1 и x ₂ = 6 (заметим, что это — корни соответствующего уравнения) нанесем на числовую прямую и определим знаки квадратного трехчлена — левой части неравенства в каждом из полученных интервалов. Имеем

Заштрихуем те интервалы, в которых квадратный трехчлен имеет нужный нам знак (знак –). (Числа x ₁ = –1 и x ₂ = +6 отмечены незакрашенными кружочками, так как неравенство строгое). Таким образом, множество решений второго неравенства (-1,6). Чтобы получить решения системы неравенств, найдем пересечение двух множеств: (-  ,2]  (-1,6) = (-1,2]. Геометрически это можно изобразить так:

Пересечением множеств является множество точек, на котором штриховки накладываются друг на друга.

Учитывая рассмотренные примеры 5 и 6, можно сделать один вывод. Множество решений системы уравнений или неравенств представляет собой пересечение множеств решений каждого из уравнений или неравенств, входящих в эту систему.

Иногда в процессе решения системы уравнений или неравенств получается некоторая совокупность других систем, к которым приводится данная система. В таких случаях множество решений исходной системы является объединением множеств решений каждой системы, входящей в эту совокупность. Разберем один пример.

Пример 7. Решить систему неравенств

.

Решение. Раскрывая модуль в первом неравенстве системы, получим два случая: 1) при и 2) при x – 6

1) или 2)

Вначале решим первую систему из этой совокупности. Здесь первое и второе неравенства линейные и имеют решения, соответственно, [6,+  ) и (-  ,12]. Третье неравенство квадратное. Решая его методом интервалов (так же, как и второе неравенство в примере 6), получим
(-  ,5)  (9,+  ). Множество решений системы есть пересечение трех множеств:

Найдем пересечение первого и второго множества:

Используя распределительный закон пересечения относительно объединения (см. §4), будем иметь

[6,12]  ((-  ,5)  (9,+  ))=([6,12]  (-  ,5))  ([6,12]  (9,+  )) =  (9,12] = (9,12].

Теперь решим вторую систему из совокупности. Проводя аналогичные рассуждения, как и в первом случае, получим три множества: (-  ,6),[4,+  ) и (-  ,5)  (9,+  ). Найдем их пересечение:
(-  ,6)  [4,+  )=[4,6);

Множество решений исходной системы является объединением множеств (9,12] и [4,5), то есть [4,5)  (9,12].

1.6. Множества точек на плоскости, задаваемые уравнениями
и неравенствами с двумя переменными

Множества точек на плоскости можно задавать их характеристическими свойствами. В разд. 1.2 мы уже познакомились с такими примерами. Кроме такого способа задания их часто задают соотношениями между координатами точек в виде уравнений или неравенств.

Пусть на плоскости выбрана система координат. Тогда любое уравнение с двумя переменными F(x,y)=0 задает множество точек на плоскости, а именно множество точек М(х,у), координаты которых удовлетворяют этому уравнению. Например, точка М(-3,4) принадлежит множеству, заданному уравнением x 2 + y 2 = 25, а точка N(1,6) не принадлежит этому множеству
(в самом деле, (–3) 2 + 4 2 = 25, тогда как 1 2 + 6 2  25). Из школьного курса известно, что уравнение y = kx + b задает прямую, а уравнение y = ax 2 + bx + c при a  0 — параболу на плоскости. Точно так же любое неравенство с двумя переменными х и у задает какое-либо множество точек на плоскости. В частности, нера­венство у>kx+b задает множество точек, лежащих выше прямой
(рис. 23). Соответственно, неравенство у

Аналогично неравенство y > ax 2 + bx + c задает множество точек, лежащих по одну сторону от параболы (рис. 25 и 26), а неравенство y ax 2 + bx + c задает множество точек, лежащих по другую сторону (рис. 27 и 28).

Когда имеется система уравнений или неравенств с двумя переменными, то множество решений такой системы представляет собой пересечение множеств решений каждого уравнения или неравенства, входящего в систему.

Пример. Построить множество точек, удовлетворяющих следующим соотношениям:

б) .

Решение. В случае а) соотношения равносильны следующей системе

.

Множество решений первого неравенства изображено штриховкой на рис. 29, а второго неравенства — на рис. 30. Прямая, изображенная на рис. 29 пунктиром, означает, что точки на этой прямой не входят в множест­во решений неравенства. Множество решений системы есть пересечение двух множеств, оно изображено на рис. 31.

Рис. 29 Рис. 30 Рис. 31

В случае б) множество решений первого неравенства изображено штриховкой на рис. 32, второго неравенства — на рис. 33, а множество точек, удовлетворяющих системе, — на рис. 34.

Рис. 32 Рис. 33 Рис. 34

1.7. Отображение множеств. Взаимно-однозначное
соответствие между множествами. Понятие числовой функции

1. Рассмотрим два множества А и В. Если каждому элементу а множества А некоторым способом поставлен в соответствие один элемент b множества В, то говорят, что задано отображение множества А в множество В. Записывают это так: f:A  B или b=f(a). Через f обозначают то отображение (правило), по которому это соответствие устанавливается. С помощью диаграмм Венна это изображается так:

Пример 1. Рассмотрим два множества: А — множество учеников в 10-м классе и В — множество стульев в аудитории. Когда начинается урок, то каждый ученик садится на стул. Тем самым устанавливается отображение множества А в множество В. При этом часть стульев может остаться незанятой (рис. 35).

Если же каждый элемент множества В соответствует какому-либо элементу множества А,
то говорят, что множество А отображается на множество В (рис. 36).

В примере 1 так будет, если все стулья окажутся занятыми (то есть количество учеников и количество стульев одинаковое).

Пример 2. Пусть множество А — ученики того же 10-го класса, а С — это множество букв в русском алфавите. Тогда множество А можно отобразить в множество С так: поставить каждому ученику в соответствие ту букву, с которой начинается его фамилия. При этом может оказаться так, что в классе несколько человек имеют фамилии, начинающиеся с одной буквы. Тогда всем им будет поставлена в соответствие одна и та же буква.

Между множествами А и В установлено взаимно-однозначное соответствие (взаимно-однозначное отображение), если каждому элементу а из А поставлен в соответствие один элемент b из B, и при этом соответствии каждый элемент b из В соответствует одному и только одному элементу а из А. С помощью диаграмм взаимно-однозначное соответствие изображено на рис. 36.

В примере 1 отображение f:A  B будет взаимно-однозначным только тогда, когда все стулья окажутся занятыми (и на одном стуле будет сидеть только один ученик, а не два, — учитель этого не допустит!)

В примере 2 отображение f:A  С никогда не будет взаимно-однозначным, так как, вообще говоря, количество учеников в классе всегда меньше количества букв и, кроме того, ни одна фамилия не начинается с буквы “й” или “ь”.

Приведем теперь примеры взаимно-однозначного соответствия бесконеч­ных множеств. Одним, наиболее хорошо всем знакомым, является взаимно-однозначное соответствие между множеством всех действительных чисел R и множеством точек на прямой (числовая прямая). Разберем и другой пример. Выберем на плоскости систему координат и поставим в соответствие каждой окружности вписанный в нее квадрат, стороны которого параллельны осям координат. Мы получим взаимно-однозначное соответствие между множеством всех окружностей и множеством всех квадратов, стороны которых параллельны осям координат. Другое взаимно-однозначное соответствие между этими множествами получается, если сопоставить каждой окружности описанный вокруг нее квадрат, стороны которого параллельны осям координат.

Далее рассмотрим множество А всех точек на плоскости и множество В всех окружностей на этой плоскости, имеющие заданный радиус R. Если поставить в соответствие каждой точке а окружность радиуса R с центром в этой точке, то получим взаимно-однозначное соответствие между множествами А и В.

2. Предположим теперь, что множества А и В — числовые. Например, какие-либо интервалы, конечные или бесконечные. В этом случае одно мно­жество будем обозначать буквой D и его элементы х:х  D; другое множество обозначим через F, а его элементы у:у  F.

Отображение числового множества D в числовое множество F называют функцией (числовой функцией) и записывают это так: у=f(x). Множество D называют областью определения,
а элемент х — аргументом. Множество F называют областью значений, а элемент у — значением функции.

Функцию можно задавать разными способами. Одним из способов является табличный. Например, таблица

задает взаимно-однозначное соответствие у=f(x) между множеством D= <1,2,3,4,5. >и множеством Ф=<6,7,8,9,10. >. Это же соответствие можно задать аналитически (по формуле): у=х+5, где х  N — множество натуральных чисел. Наконец, то же соответ­ствие можно задать графически:

В дальнейшем, в гл. 4 мы рассмотрим подробно другие примеры функций. А сейчас остановимся только на одной — функции Дирихле. Эта функция равна единице в рациональных точках и нулю в иррациональных точках. Таким образом, функция Дирихле — это отображение множества всех чисел R в множество Ф=<0,1>. Конечно, оно не является взаимно-однозначным. Функцию Дирихле уже невозможно задать с помощью таблицы или графически, и аналитически она имеет довольно сложный вид:

.

1.8. Эквивалентные множества. Счетные и несчетные множества. Мощность множества.

1. Два множества называют эквивалентными, если между ними можно установить взаимно-однозначное соответствие. Проще всего проверить эквивалентность конечных множеств. Для двух конечных множеств взаимно-однозначное соответствие можно установить лишь в случае, когда они имеют одинаковое количество элементов. Поэтому конечные множества эквивалентны тогда и только тогда, когда они имеют поровну элементов. Для бесконечных множеств не имеет смысла говорить о числе элементов. Однако и среди бесконечных множеств можно найти эквивалентные.

2. Рассмотрим множество всех натуральных чисел N=<1,2,3,4. >. Любое бесконечное подмножество А множества N эквивалентно самому множеству N. В самом деле, элементы этого подмножества можно расположить в порядке возрастания и каждому поставить в соответствие его порядковый номер (перенумеровать). Получим Так как элементов в подмножестве А бесконечно много, этот процесс можно неограниченно продолжать. Тем самым устанавливается взаимно-однозначное соответствие между А и N. Нетрудно догадаться, что множество А представляет собой числовую последовательность. Таким образом, все числовые последователь­ности, содержащие различные элементы, эквивалентны множеству натуральных чисел N.

Рассмотрим теперь множество Z всех целых чисел:

На первый взгляд кажется, что это множество невозможно перенумеро­вать. Ведь если мы начнем нумерацию, скажем, с числа 0, а потом будем нумеровать вправо, то все отрицательные числа окажутся незанумерованными. Если же мы будем нумеровать влево, то незанумерованными окажутся все положительные числа. Однако эту нумерацию можно осуществить, применив следующую хитрость: двигаться не в одном направлении, а все время менять его. Иными словами, будем нумеровать так: числу 0 дадим номер 1,числу 1 — номер 2, числу -1 — номер 3, числу 2 — номер 4, числу -2 — номер 5 и т.д. Мы получили, таким образом, взаимно-однозначное соответствие между множествами Z и N. Следовательно, Z и N также экви­валентны.

Еще сложнее занумеровать все точки плоскости, обе координаты которых — целые числа (рис. 37). Эти точки образуют, как говорят, решетку. Чтобы занумеровать все точки решетки, можно, например, вести нумерацию по “раскручивающейся спирали” так, как изображено на рис. 37.

Бесконечные множества, эквивалентные множеству натуральных чисел, называются счетными множествами. Иными словами, если элементы бесконечного множества можно перенумеровать, то такое множество называется счетным. Самым простым примером счетного множества является само множество N натуральных чисел. Более сложные примеры счетных множеств мы рассмотрели выше.

Теперь сформулируем основные теоремы о счетных множествах.

Теорема 1. Каждое бесконечное подмножество А счетного множества В счетно.

Теорема 2. Объединение конечного или счетного множества счетных множеств счетно.

Доказывать эти теоремы мы не будем, хотя отметим, что доказательство теоремы 1 почти ничем не отличается от приведенного выше рассуждения, когда доказывалась эквивалентность между множеством N и его подмножест­вом А.

3. До сих пор мы рассматривали лишь такие бесконечные множества, которые являются счетными. Однако не все бесконечные множества счетные, существуют и такие, элементы которых нельзя перенумеровать. Простейшим примером такого множества является множество всех точек конечного интервала, например, интервала (0,1). Ясно, что в этом множестве содержится счетное подмножество. В качестве такого подмножества можно указать, например, числовую последовательность . Но оказывается, что точек в интервале (0,1) “намного” больше, чем точек этой последователь­ности. Точнее говоря, множество точек интервала (0,1) несчетно, то есть нельзя установить взаимно-однозначного соответствия между множеством точек интервала (0,1) и множеством натуральных чисел N. Доказательство этого утверждения мы проводить не будем. Легко сообразить, что любой другой интервал длины 1 на числовой прямой эквивалентен интервалу (0,1). Вообще, произвольный интервал (a,b) конечной длины эквивалентен интервалу (0,1). Взаимно-однозначное соответствие между ними можно установить так, как показано на рис. 38.

Точно так же любой отрезок (замкнутый интервал) эквивалентен отрезку [0,1] (рис. 39).

” Это не удивительно” — скажете вы, — “они же конечные”. Но удивительно то, что и бесконечный интервал эквивалентен конечному интервалу. Например, вся числовая прямая эквивалентна интервалу (-1,1)! Показать это можно следующим образом (рис. 40). Сначала точке a  (-1,1) сопоставляется лежащая под ней точка b полуокружности, а потом точка b сопоставляется точке с, лежащей на нашей прямой (точка O₁ — центр полуокружности, незакрашенные кружочки означают, что эти точки не принадлежат множествам).

4. Теперь мы попробуем сравнивать множества: какое из множеств имеет “больше” элементов, какое “меньше”. В случае конечных множеств это несложно, их элементы можно пересчитать. Для бесконечных множеств это невозможно. Тут нам поможет отношение эквивалентности. Оно выделяет среди всех множеств (конечных и бесконечных) те множества, которые обладают некоторым общим свойством. Назовем это общее свойство мощностью множества и будем говорить, что все эквивалентные между собой множества имеют одинаковую мощность. Для конечного множества мощность — это количество его элементов. Для счетных множеств — это мощность множества натуральных чисел N, которая обозначается специальной буквой  ₀ (алеф-нуль). Мощность множеств, эквивалентных множеству всех действительных чисел, называется мощностью континуума (от латинского continuum — непрерывный). Такая мощность обозначается буквой С или 2  0 . Мощность есть фундаментальное понятие теории множеств, принадлежащее Г. Кантору. Таким образом, в п. 2 мы рассматривали множества мощности  ₀, а в п.3 — множества мощности континуума.

Замечание. Внимательный читатель заметит, что эквивалентность открытых интервалов между собой и с числовой прямой если и не была доказана строго, то по крайней мере иллюстрировалась на рисунках, равно как и эквивалентность замкнутых интервалов между собой. Но об эквивалент­ности интервала (0,1) и отрезка [0,1] ничего не было сказано. На самом деле
они тоже эквивалентны. Для этого выберем в интервале (0,1) последователь­ность точек . Точке поставим в соответствие точку 0, точке — точку 1, точке — точку , точке — точку и т.д. Далее, если точка х  (0,1) и не имеет вид , то этой точке поставим в соответствие такую же точку х  [0,1]. Таким образом установлено взаимно-однозначное соответствие между (0,1) и [0,1]. Что и требовалось доказать. Значит, мощности (0,1) и [0,1] одинаковы и равны 2  0 . Более удивителен следующий факт.

Теорема. Множество точек квадрата имеет мощность континуума 1 .

Это утверждение означает, что квадрат содержит “столько же” точек, что и отрезок, хотя на первый взгляд кажется, что в нем должно быть “гораздо больше” точек. Доказательство этой теоремы мы приводить не будем. Кстати сказать, множества точек плоскости и пространства тоже имеют мощность континуума.