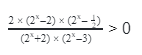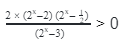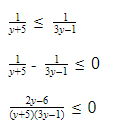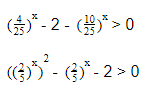Неравенство в степени квадратное уравнение

11.3.5. Решение показательных неравенств, приводящихся к квадратным неравенствам

При решении показательных неравенств, приводящихся к квадратным неравенствам, поступают так же, как в примерах решения показательных уравнений, приводящихся к квадратным уравнениям, т. е. делают замену переменных, получают квадратное неравенство, которое решают, а затем возвращаются к прежней переменной.

Решить неравенство:

1) (0,5) 2 x +2 x .

Сделаем замену: пусть (0,5) х =у. Получаем неравенство:

у 2 +2 2 -3y+2 2 -3y+2 на линейные множители по формуле:

ax 2 +bx+c=a (x-x₁)(x-x₂), где х₁ и х₂ – корни квадратного уравнения ax 2 +bx+c=0.

Находим корни приведенного квадратного уравнения y 2 — 3 y+ 2 =0. Дискриминант D=b 2 -4ac=3 2 -4∙1∙2=9-8=1=1 2 . Так как дискриминант является полным квадратом, то применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

у₁+у₂= 3 , у₁∙у₂= 2 . Отсюда: у₁= 1 , у₂= 2 . Значит, y 2 -3y+2=(у- 1 )(у- 2 ).

Решаем неравенство: (у-1)(у-2) 1 ; 2 ), отсюда: (0,5) х є( 1 ; 2 ).

(0,5) х = 1 → (0,5) х = (0,5) 0 → х=0.

(0,5) х = 2 → ( 1 /₂) x = 2 → 2 — x = 2 1 → -x=1; x=-1. Значит, хє(-1; 0).

2) 9 x -1 x -1 +6.

Представим 9 х-1 в виде степени числа 3.

3 2 ( x -1) x -1 +6. Сделаем замену: 3 х-1 =у. Тогда получается квадратное неравенство: у 2 2 -у-6 2 -у-6=0. Проверим, возможно ли применить теорему Виета, ведь ею пользуются только, если корни являются целыми числами. Гарантией этого будет дискриминант, который должен быть полным квадратом некоторого числа. Находим дискриминант D=b 2 -4ac=1-4∙(-6)=1+24=25=5 2 . Дискриминант является полным квадратом числа 5, поэтому, подбираем корни, пользуясь теоремой Виета: у₁+у₂=1, у₁∙у₂=-6. Подходят значения: у₁= -2 и у₂= 3 .

Раскладываем левую часть неравенства на линейные множители, получаем:

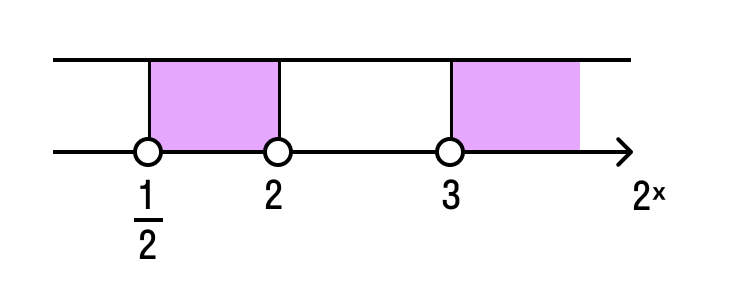
(у +2 )(у- 3 ) -2 ; 3 ). Возвращаемся к переменной х:

3 х-1 є( -2 ; 3 ), но так как отрицательных значений степень 3 х-1 принимать не может, то запишем: 3 х-1 є( 0 ; 3 ). Определим интервал значений переменной х.

3 х-1 → 0 при х-1 → -∞, так как число 3 в степени, стремящейся к минус бесконечности, фактически будет равным нулю, значит, х→ -∞ .

Далее, 3 х-1 = 3 → 3 х-1 = 3 1 → х-1=1 → х=2.

Показательные неравенства

О чем эта статья:

10 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение показательных неравенств

Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a f(x) > a g(x) , a f(x) g(x) .

Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.

Для изучения этой темы стоит повторить:

И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.

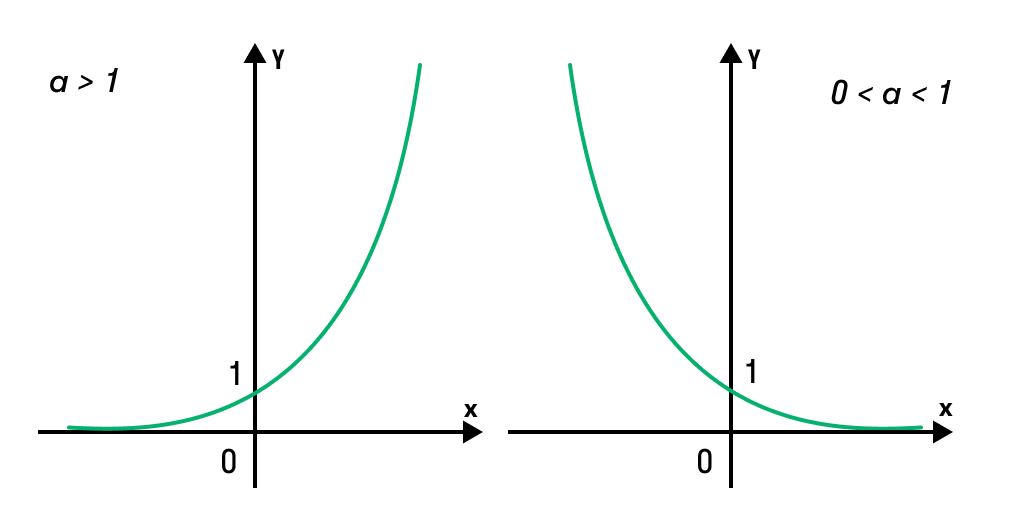
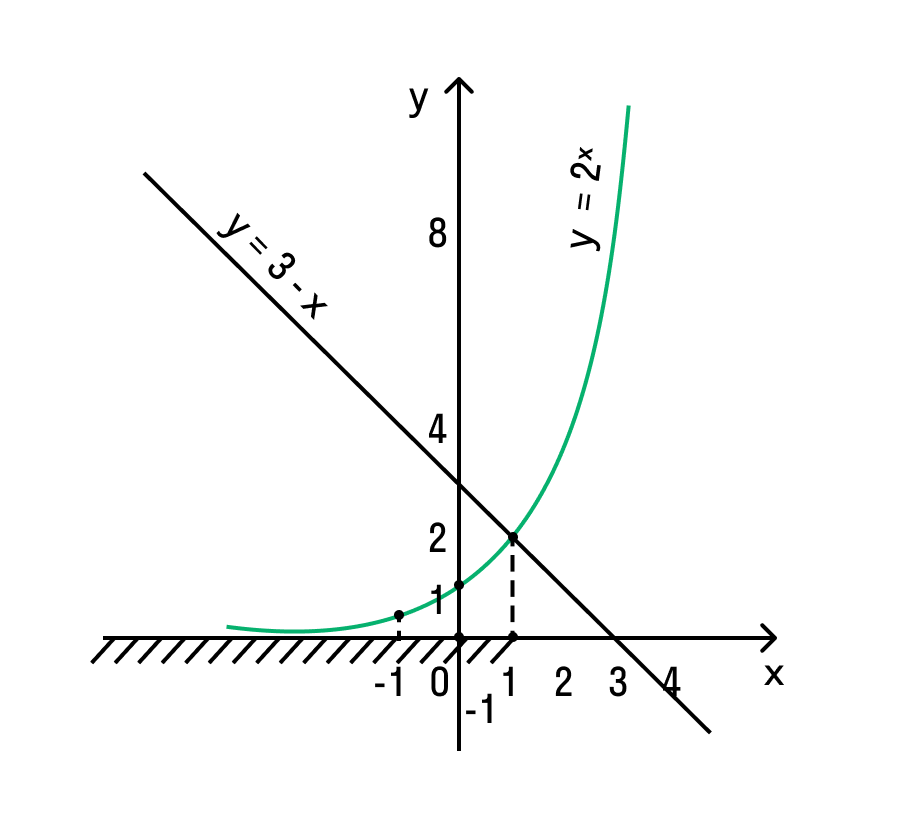
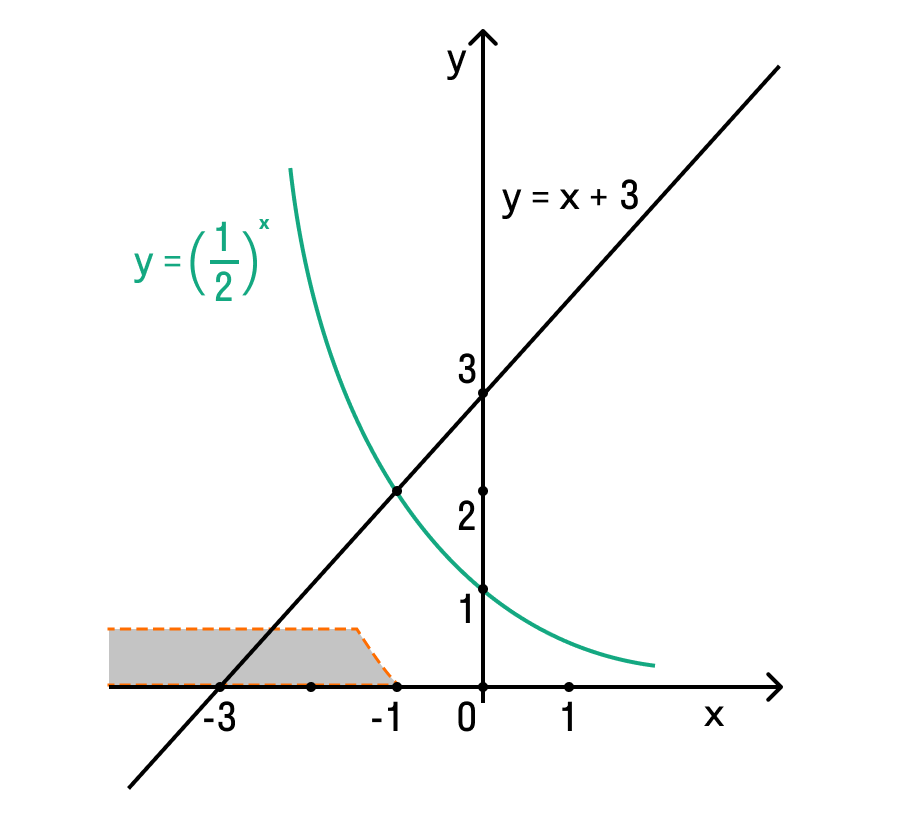
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x , где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.

При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2 -2 = 4, 2 -4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.

Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений.

Запишем следствие монотонности показательной функции в виде формул:

• a f(x) > a g(x) f(x) > g (x), когда функция возрастает, т. е. а > 1;
• a f(x) > a g(x) f(x)

Как решать показательные неравенства

Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости.

Допустим, у нас есть простейшее показательное неравенство:

Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:

Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:

Проверим, верно ли в таком случае х > 2.

0,5 3 = 0, 125 и т. д.

Как видите, на самом деле в этом случае х

Если а > 1, то a x > a n a > n, и при решении неравенства можно просто убрать одинаковые основания степени.

Если 0 x > a n a

Наконец, если рассмотреть случай, когда а х > 9

Логичное, на первый взгляд, предположение, что х > 2, не выдержит проверки, потому что:

Если продолжить этот ряд, знаки будут чередоваться, и наш корень будет попеременно то меньше, то больше 2. Поэтому для ясности всегда предполагается, что основание степени — положительное число.

Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Показательные неравенства, сводящиеся к простейшим

Решая показательные уравнения, вы наверняка первым делом исследовали их на возможность приведения к одинаковым основаниям или одинаковым степенным функциям. Так вот, с неравенствами можно делать то же самое! Помните лишь о смене знака, если основание степени меньше единицы. И да пребудет с вами сила. 😎

Попробуем на примере несложного показательного неравенства с разными основаниями.

Пример 1

Поскольку 3 больше 1, знак не меняем:

Показательные неравенства, сводящиеся к квадратным

Снова давайте вспомним, как аналогичный метод применялся к показательным уравнениям. Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.

Пример 1

Наименьший общий множитель в данном случае будет 3 х , обозначим его новой переменной у и перенесем все слагаемые в левую сторону.

(3 х ) 2 — 12 × 3 х + 27 х = у

y 2 — 12y + 27 х 1 х 2

Поскольку 3 > 1, мы не меняем знак.

1 2 x — 5 sinx + 2 2 — 5y + 2

Показательные неравенства, сводящиеся к рациональным

Как вы, наверное, помните из предыдущего курса алгебры, рациональные показательные неравенства — это такие, в которых левая и правая часть представляют собой дробно-рациональные функции. Метод их решения таков: нужно перенести все в левую часть, чтобы в правой остался лишь ноль, и привести к общему знаменателю. Далее решаем уравнение, отмечаем все корни на оси и применяем метод интервалов (если забыли, что это такое — повторите).

Важно помнить: если в числителе и знаменателе встретятся одинаковые множители с переменной, сокращать их нельзя.

Пример 1

Преобразуем неравенство указанным выше способом:

(обратите внимание, мы избавились от минуса в числителе и поменяли знак неравенства).

Поскольку выражение 2 х + 2 в любом случае будет больше нуля, мы можем смело его исключить из неравенства.

(2 х — 2) × (2 х — 1/2) × (2 х — 3) > 0

Пример 2

Обозначим 3 х через новую переменную y:

3 х = y, при условии что 3 х > 0.

Применим метод интервалов и получим:

Вернем на место нашу старую переменную:

Однородные показательные неравенства

Однородными называются такие показательные неравенства, где в каждом слагаемом сумма степеней одинакова.

Иногда такие выражения бывают очень длинными и запутанными, но не стоит этого пугаться. Практически все неравенства с однородными показательными функциями решаются по одному принципу: стараемся упростить выражение, разделив его на одночлен, а затем при необходимости делаем замену переменных.

Пример 1

4 х — 2 × 5 2х — 2 х × 5 х > 0

2 × 2 х — 2 × 5 2х — 2 х × 5 х > 0

В левой части неравенства мы видим однородные функции относительно 2 х и 5 х . Следовательно, можно разделить обе части на 2 2х или 5 2х . Выберем 5 2х , т. е. 25 х . В итоге у нас получится:

Если обозначить (2/5) х новой переменной y, получим квадратное неравенство:

Неравенства, решаемые графическим методом

Этот метод решения показательных неравенств — самый наглядный, и для многих он может показаться самым простым. Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Если бы мы имели дело с уравнением, эта точка стала бы корнем.

Но поскольку мы рассматриваем неравенства, нужно будет выделить искомую область. Для неравенства f(x) > g(x) это будет та область, где график функции f(x) находится выше.

Пример 1

2 х х и 3 — х, а также точка их пересечения.

Очевидно, что точкой пересечения является х = 1, при этом график функции 2 х ниже в области от -∞ до 1.

Пример 2

Начертим графики этих двух функций, чтобы найти точку пересечения.

Искомой точкой будет х = -1, а областью, где функция (1/2) х находится выше — диапазон от -∞ до -1.

Квадратные неравенства, примеры, решения

В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.

Что представляет собой квадратное неравенство

Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.

Квадратное неравенство – это такое неравенство, которое имеет вид a · x 2 + b · x + c 0 , где a , b и c – некоторые числа, причем a не равно нулю. x – это переменная, а на месте знака может стоять любой другой знак неравенства.

Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y = a · x 2 + b · x + c .

Приведем пример квадратного неравенства:

Возьмем 5 · x 2 − 3 · x + 1 > 0 . В этом случае a = 5 , b = − 3 и c = 1 .

Или вот такое неравенство:

− 2 , 2 · z 2 − 0 , 5 · z − 11 ≤ 0 , где a = − 2 , 2 , b = − 0 , 5 и c = − 11 .

Покажем несколько примеров квадратных неравенств:

Здесь коэффициенты этого квадратного неравенства есть ; 1 2 3 · x 2 — x + 5 7 0 , в этом случае a = 1 2 3 , b = — 1 , c = 5 7 .

Особое внимание нужно обратить на тот факт, что коэффициент при x 2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b · x + c > 0 , так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.

Пример такого неравенства x 2 − 5 ≥ 0 .

Способы решения квадратных неравенств

Основным метода три:

• графический;
• метод интервалов;
• через выделение квадрата двучлена в левой части.

Графический метод

Метод предполагает проведение построения и анализа графика квадратичной функции y = a · x 2 + b · x + c для квадратных неравенств a · x 2 + b · x + c 0 ( ≤ , > , ≥ ) . Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.

Метод интервалов

Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a · x 2 + b · x + c при их наличии.

Для неравенства a · x 2 + b · x + c 0 решениями являются промежутки со знаком минус, для неравенства a · x 2 + b · x + c > 0 , промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.

Выделение квадрата двучлена

Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида ( x − p ) 2 q ( ≤ , > , ≥ ) , где p и q – некоторые числа.

Неравенства, сводящиеся к квадратным

К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.

Приведем пример. Рассмотрим равносильное преобразование неравенства 5 ≤ 2 · x − 3 · x 2 . Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3 · x 2 − 2 · x + 5 ≤ 0 .

Необходимо найти множество решений неравенства 3 · ( x − 1 ) · ( x + 1 ) ( x − 2 ) 2 + x 2 + 5 .

Решение

Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:

3 · ( x − 1 ) · ( x + 1 ) − ( x − 2 ) 2 − x 2 − 5 0 , 3 · ( x 2 − 1 ) − ( x 2 − 4 · x + 4 ) − x 2 − 5 0 , 3 · x 2 − 3 − x 2 + 4 · x − 4 − x 2 − 5 0 , x 2 + 4 · x − 12 0 .

Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.

D ’ = 2 2 − 1 · ( − 12 ) = 16 , x 1 = − 6 , x 2 = 2

Построив график, мы можем увидеть, что множеством решений является интервал ( − 6 , 2 ) .

Ответ: ( − 6 , 2 ) .

Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2 · x 2 + 5 x 2 + 6 · x + 14

равносильно квадратному неравенству x 2 − 6 · x − 9 0 , а логарифмическое неравенство log 3 ( x 2 + x + 7 ) ≥ 2 – неравенству x 2 + x − 2 ≥ 0 .