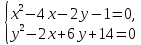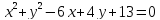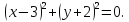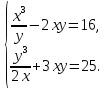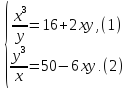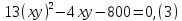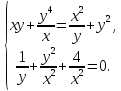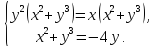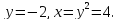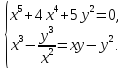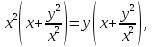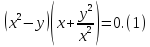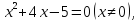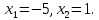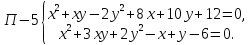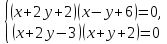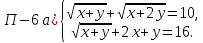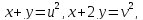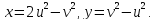Нестандартные методы решения систем уравнений

Нестандартные способы решения систем линейных уравнений

Рецензия

на проектно-исследовательскую работу по математике ученика 8 класса «А» МБОУ «Гимназии №20» Кислякова И. на тему: «Нестандартные способы решения систем линейных уравнений».

Руководитель: учитель математики Родионова Н.Е.

Актуальность данной темы подтверждается множеством причин. Рассматриваемые в научно-исследовательской работе вопросы актуальны в связи с проведением государственной итоговой аттестации и единого государственного экзамена по математике, в котором всегда встречается решение систем уравнений. Кроме того, данная тема изучается на первом курсе университета при изучении курса высшей математики. Что будет способствовать лучшему пониманию и усвоению материала. Также умение решать системы уравнений методом Крамера, например, дает возможность быстрее решать системы уравнений с параметром. Данная тема представляет собой практический интерес, так как ее можно реализовать с помощью компьютерной программы Excel, что особенно вызывает заинтересованность у учащихся.

Проектно-исследовательская работа состоит из двух глав, в свою очередь делящихся на 5 и 4 параграфа каждая, а также введения, заключения, списка использованной литературы и приложения. Оформление проектно-исследовательской работы соответствует принятым стандартам.

Во введении обоснована актуальность исследования, цели и задачи работы, теоретическая и практическая значимость работы. Цели и задачи проектно-исследовательской работы сформулированы грамотно, соответствуют заявленной теме.

В первой главе работы рассматриваются теоретические вопросы. Даны основные понятия и определения, которыми учащийся пользуется при изучении темы. На высоком уровне изложен материал по теме исследовательской работы. Видно, что Иван проанализировал большое количество учебников по заданной тематике, провел грамотный анализ ресурсов, использовал только достоверные данные. Перед учеником стояла сложная задача написания теоретической части работы, так как успех понимания материала зависел во многом от трудолюбия ребенка и умения «правильно» воспринимать математический язык. Всю теоретическую часть ученик писал самостоятельно, на основе собственных знаний и исследований.

Вторая глава проектно-исследовательской работы — практическая. Она содержит большое количество разобранных примеров на каждый метод решения систем линейных алгебраических уравнений, причем, которые имеют различное количество решений. Иван воплотил идею реализации решения систем линейных алгебраических уравнений в Excel, им разработано программное приложение, в котором он реализует все методы. Ученик самостоятельно разобрался с программой, смог выстроить алгоритм решения в электронной среде. Особое внимание практической части работы заслуживает умение применить способы решения систем линейных алгебраических уравнений для задач повышенной сложности: решений систем уравнений с параметром, сложных экономических задач.

В результате написания работы ученик грамотно изложил результаты исследования, на основе проделанного исследования, он сделал выводы о достоинствах и недостатках каждого из методов.

Предложенный в заключении задачник будет полезен учащимся, которые самостоятельно изучали данную тему и хотят выяснить усвоили ли они этот материал.

Работа построена последовательно, следование глав — логично. Работа оформлена в соответствии с требованиями к научно-исследовательской работе.

Работа заслуживает внимания и высокой оценки со стороны экспертной комиссии.

Рецензент: учитель математики Родионова Н.Е.

Скачать:

Вложение	Размер
prezentatsia_sistemy.pptx	832.96 КБ

Предварительный просмотр:

Подписи к слайдам:

Проектно–исследовательская работа Нестандартные способы решения систем линейных уравнений Выполнена учеником 8 класса «А» МБОУ «Гимназия № 20» Кисляковым Иваном Сергеевичем Руководитель учитель математики Родионова Наталья Евгеньевна Донской, 2012

Целью работы является изучение методов решения систем линейных уравнений и построение компьютерной модели этих решений систем линейных уравнений с помощью приложения MS Excel 2010. Для достижения цели поставлены следующие задачи : 1. изучить литературу по данной теме; 2. охарактеризовать каждый метод в отдельности; 3. применить изученные методы на практике; 4. на основе алгоритмов изученных методов создать компьютерные модели решения системы линейных уравнений в MS Excel 2010; 5. провести сравнительный анализ методов, выявить их достоинства и недостатки.

Метод Крамера Метод Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

Рассмотрим стандартную линейную систему трех уравнений Введем определитель системы, составленный из коэффициентов при неизвестных Введём дополнительные определители Δ Δ1 Δ2 Δ3 Число решений 0 0 0 0 Бесконечное множество решений 0 ≠0 ≠0 ≠0 Нет решений ≠0 любое любое любое Единственное решение

Найти решение системы трех уравнений с тремя неизвестными методом Крамера : x = ; y = Найти решение системы трех уравнений с тремя неизвестными методом Крамера : Решение: 1. Составим определитель системы 2. Вычислим дополнительные определители 3 . Найдем решение уравнения:

Метод Гаусса Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида , из которого последовательно, начиная с последних переменных , находятся все остальные переменные.

Пусть исходная система выглядит следующим образом. , где Алгоритм решения методом Гаусса заключается в следующем: 1) На первом этапе (прямой ход) необходимо записать расширенную матрицу системы. 2 ) На втором этапе осуществляется так называемый обратный ход снизу вверх.

Найти решение системы трех уравнений с тремя неизвестными методом Гаусса: Решение: 1) Прямой ход 2) Обратный ход Ответ:

Пусть дана система линейных уравнений с n неизвестными: Найдем определитель матрицы системы det A. Находим обратную матрицу A — 1 к матрице системы. , где Матричный метод X = A − 1 B

Решить матричным способом: Решение: Найдем определитель: Запишем обратную матрицу: Ответ:

Исследовать при каких значениях k значение переменной х больше, чем значение переменной у . Решение: Решим систему методом сложения: Решим систему методом Крамера : 4k+15>6-3k , k>- Ответ: при k>-

(ЕГЭ – 2005, С-2): При каких значениях параметра а уравнение имеет ровно одно решение? Решение: Ответ: При уравнение имеет ровно одно решение.

Реализация методов решения систем линейных алгебраических уравнений в MS Excel 2010

Название метода Метод Крамера Метод Гаусса Матричный метод Достоинства формулы Крамера легко запоминаются; пригоден для решения систем линейных уравнений 2 и 3 порядков; позволяет решать систему линейных уравнений в общем виде; позволяет избежать лишних записей. применим к любой системе линейных уравнений; менее трудоемкий; позволяет однозначно установить, совместна система или нет. не вызывает затруднений при работе на компьютере. Недостатки высокая ресурсоемкость вычислений определителей; для систем уравнений порядка выше 3 затруднен подсчет определителей; если система имеет бесконечное число решений, чтобы записать общий вид ответа нужно обратиться к Гаусса не позволяет найти общие формулы, выражающие решение системы через ее коэффициенты и свободные члены, которые необходимы для написания программы на компьютере. высокая ресурсоемкость вычисления обратной матрицы; если система имеет бесконечное число решений, чтобы записать общий вид ответа нужно обратиться к методу Гаусса.

«Мне приходится делить своё время между политикой и уравнениями. Однако уравнения по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно. А. Эйнштейн

Нестандартные алгебраические системы уравнений

Мы будем рассматривать только системы уравнений, в которых число уравнений совпадает с числом неизвестных, ибо в плане эффективного, технологичного нахождения множества решений перспективно рассмотрение только таких систем.

Просмотр содержимого документа
«Нестандартные алгебраические системы уравнений»

Тема: «Нестандартные алгебраические системы уравнений»

Решение нестандартных алгебраических систем уравнений. (Основные понятия и методы решений).

1. Основные понятия

2. Различные преобразования и методы решений

3. Решение нестандартных алгебраических систем уравнений известными способами и методом — три «З».

Решение нестандартных алгебраических систем уравнений.

Цель: научиться решать системы уравнений разными способами и известными методами.

Проблема данного исследования: как применять методы при решении систем алгебраических уравнений.

Объектом исследования будут служить нестандартные алгебраические системы уравнений

Предметом – применение методов и различных способов решения алгебраических систем уравнений.

1. Рассмотреть основные понятия систем с двумя и тремя неизвестными (переменными), преобразования и методы решений.

2. Научиться применять различные методы и известные способы при решении нестандартных алгебраических систем уравнений.

3. Обосновать применение метода: Три — «З» при решении нестандартных алгебраических уравнений.

4. Создать компьютерную программу для решения примеров вида П-1и П-11.

Единых способов решения систем нестандартных алгебраических уравнений нет, этот раздел в алгебре считается по праву трудным, поэтому исследуемая тема сегодня особенно актуальна и востребована, особенно при сдаче ЕГЭ, на олимпиадах и конкурсах.

На вступительных экзаменах (где они ещё проводятся) в вузах предлагаются задачи, в которых требуется решить системы алгебраических уравнений или неравенств. Этот раздел алгебры по праву считается одним из трудных, так как нет единых способов решения нетрадиционных систем алгебраических уравнений.

Многие учащиеся вопрос о нахождении решений системы уравнений понимают как формальное выполнение ряда алгебраических преобразований и не обосновывают законность выполняемых преобразований, которые могут привести как к появлению посторонних решений, так и к потере решений. В работе рассмотрим основные понятия и виды различных преобразований систем уравнений с двумя и тремя неизвестными. Решим несколько уравнений своим методом три — «З» (задать, заметить, заключить) и несколько нетрадиционных систем уравнений известными способами, которые ещё надо заметить методом пристального взгляда и применить их.

Решение нестандартных алгебраических систем уравнений.

1. Основные понятия.

Будем рассматривать системы с двумя и тремя неизвестными (переменными). Систему двух уравнений с двумя неизвестными x и y можно записать в виде

(1)

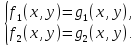
Если левые и правые части уравнений системы (1) являются многочленами от x и y или представляются в виде отношения многочленов, то систему (1) называют алгебраической.

Решением системы (1) называется пара чисел x, y, при подстановке которых соответственно вместо x и y каждое уравнение системы (1) становится верным числовым равенством. Множество решений системы может быть, в частности, пустым. В этом случае говорят, что система не имеет решений (несовместна).

Процесс решения системы обычно состоит в последовательном переходе с помощью некоторых преобразований от данной системы уравнений к другим, более простым, которые мы умеем решать. При этом нужно внимательно следить за тем, чтобы не потерять решения. Что касается посторонних решений для данной системы, то их обычно отсеивают с помощью проверки.

Если в результате преобразований системы (1) получена система:

(2)

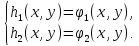
такая, что каждое решение системы (1) является решением системы (2), то система (2) называется следствием системы (1).

называют следствием системы (1), если равенство

является верным для каждой пары чисел x, y, образующих решение системы (1).

Если система (2) является следствием исходной системы (1), а система (1) также является следствием системы (2), то эти системы называют равносильными. Иначе говоря, системы называют равносильными, если множества их решений совпадают. В частности, две системы, не имеющие решений, являются равносильными.

Используя определения равносильности и следствия, можно утверждать, что:

1) если в системе уравнений заменить какое-либо уравнение равносильным, а остальные уравнения оставить без изменения, то полученная при этом система будет равносильна исходной;

2) если к данной системе присоединить уравнение, являющее следствием этой системы, то полученная система будет равносильна исходной;

3) если какое-либо уравнение данной системы заменить его следствием, а остальные уравнения оставить без изменения, то полученная система будет следствием исходной.

Общие средства перехода к равносильной системе немногочисленны. Отметим, во-первых, что простейшие преобразования любого из уравнений системы, такие как перенос, из одной части в другую, вынесение общего множителя за скобки, раскрытие скобок и т. п., не влияют на множество решений, так что приводят к равносильным системам.

Далее, чтобы перейти к равносильной системе, можно выполнить одно из следующих действий:

умножить какие-то из уравнений системы на числа (коэффициенты) и на место одного из затронутых уравнений поставить полученную сумму с коэффициентами;

в одном из уравнений выразить одну неизвестную через остальные и подставить полученное выражение во все оставшиеся уравнения, оставив, разумеется, в системе и данное уравнение;

заменить какое-либо уравнение равносильным ему соотношением (уравнением, системой или совокупностью).

2. Преобразования и методы

При решении систем уравнений нередко приходится применять такие преобразования систем:

как умножение обеих частей уравнения на одно и то же число (или одну и ту же функцию),

почленное сложение, вычитание, умножение и деление уравнений системы, возведение обеих частей уравнения в n-ю степень,

а также часто применяется метод подстановки (метод исключения неизвестного),

с помощью которого решение системы с двумя неизвестными сводится к решению уравнения с одним неизвестным.

Одним из распространённых способов решения систем является замена переменных. Допустим, что в системе удалось выделить какие-то повторяющиеся выражения, составленные из переменных. Тогда если каждое из них обозначить одной новой буквой (разумеется, разные выражения разными буквами), иначе говоря, сделать замену переменных, то наша система превращается в некоторую другую систему относительно новых неизвестных. Если её удаётся решить, то после этого для нахождения корней исходной системы предстоит решить одну или несколько систем, связывающих новые неизвестные со старыми.

3. Метод — три «З» (задать, заметить, заключить). Алгебраические системы:

Найдите действительные решения системы уравнений (1-10).

Мы придумали особый метод для решения алгебраических систем уравнений:

Метод — три «З» (задать, заметить, заключить).

Замечание: применить способ сложения -2 -ое «З»

Заключение: решить, проверить, ответить-3-ье «3»

Решение. Сложив уравнения системы, получим

Пара чисел x = 3 и y = −2, как показывает проверка, образует решение системы.

П –2

Замечание -2-ое –«З»: применить почленное умножение

Заключение -3ье-«З»: решение, (если треб. проверить), ответ

Решение. Запишем систему в виде

Перемножив почленно уравнения этой системы, получим уравнение

которое вместе с одним из уравнений системы (1)−(2) образует систему, равносильную системе (1)−(2).

Из уравнения (3) находим

то есть

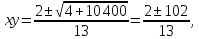
xy = 8 или xy = .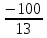

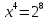
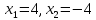
Если xy = 8, то из уравнения (1) следует, что , откуда и тогда

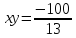
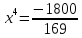
Если , то . Это уравнение не имеет действительных корней.

Замечание -2ое-«З»: xy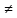0

Задание -1-3 (первое –«З»)

Заключение -3-ье-«З»: решение, (если треб. проверить), ответ

Решение. Так как 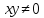, то систему можно записать в виде

Если 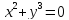, то из второго уравнения следует, что y = 0, что невозможно.

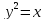
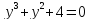
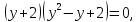
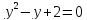
Если , то из второго уравнения системы следует, что или откуда y = −2 (уравнение не имеет действительных корней). Итак,

Задание -1-3 (первое –«З»)

П-4

Замечание -2-ое-«З»: Разложить на множители

Заключение -3-ье –«З»: решение, (если треб. проверить), ответ

Решение. Второе уравнение исходной системы равносильно каждому из уравнений

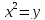
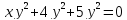
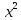
а) Если , то из первого уравнения исходной системы получаем , откуда следует, что либо y = 0, либо x = −9. Но если y = 0, то x = 0, а при x = 0 уравнение (1) теряет смысл. Итак, x = −9, y = = 81.

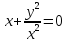
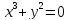
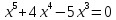
б) Если , то . Из первого уравнения системы находим

или

откуда

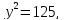
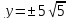
Пусть x = −5, тогда откуда .

Пусть x = 1, тогда 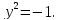Это уравнение не имеет действительных корней.

Таким образом, система имеет три действительных решения: (−9; 81), , .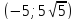

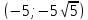
Ответ: (−9; 81), , .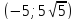

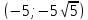
Указание. Решить каждое из уравнений системы как квадратное относительно x или y. Тогда исходная система преобразуется к виду

и равносильна совокупности четырех систем линейных уравнений.

Решение. Пусть 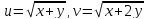, тогда

откуда:

Поэтому исходная система примет вид

Так как u ≥ 0, то u = 4, то есть

П-6 б) Решить уравнение:

Возведём обе части уравнения в третью степень:

Получим: 14-3 • • ( — = х 3

Разложим на множители левую часть уравнения.

Делители свободного члена (-14):

Методом подбора найдём корень: х=2

Разделим х 3 +3х – 14 на х-2, получим (х-2) • (х 2 +2х +7) =0

х 2 +2х +7=0 – не имеет корней, Д 0

х=2, 8+6-14=0, 14=14 –верно. Ответ: х=2

Решение. Область определения уравнения – множество точек таких, что

Преобразуем первое уравнение системы так:

Из (2) и второго уравнения системы получаем или

откуда , так как Тогда Отсюда и из (2) находим

Пара чисел удовлетворяет условиям (1).

, а из второго уравнения находим Поэтому

Пара чисел (12; −2) – решение исходной системы.

8. Решить систему уравнений с тремя неизвестными.

Решение. (Заменой переменных).

Обозначим и запишем исходную систему в следующем виде (1)

Сложив уравнения системы (1) и обозначив получим уравнение , откуда

Подставляя найденные значения суммы в систему (1), найдем искомые значения

9. Решить систему уравнений с тремя неизвестными.

Решение. Складывая уравнения попарно, получим систему

равносильную исходной системе. Перемножим уравнения этой системы и обозначим тогда , или

Решение. Вычитая из первого уравнения второе, получим

Разложим на множители левую часть уравнения:

Заметим, что исходная система равносильная системе, состоящей из ее первого и третьего уравнений и уравнения (1), равносильная также совокупности трех систем, получаемых присоединением к первому и третьему уравнениям соответственно уравнений: (2) (3) (4)

1) Подставляя из уравнения (2) в первое и третье уравнения исходной системы, получаем

Если или то из (5) следует, что 0 = 3.

Если , то из (5) находим

В этом случае система имеет два решения

2) Подставляя (см. (3)) в первое и третье уравнения исходной системы, получаем

Если то из уравнения (6) следует, что 0 = 3.

Если то из уравнения(6) находим

В этом случае система имеет решения

3) Подставляя (см. (4)) в первое и третье уравнения исходной системы, получаем:

Если то из уравнения (7) следует, что 0 = 3.

Если то из уравнения(7) находим

В этом случае система имеет два решения

Системы, содержащие логарифмы

которые удовлетворяют неравенству

Решение. Потенцируя, получаем систему

которая является следствием исходной системы.

а) Пусть и, с учетом условия из первого уравнения системы (1) получаем

Тогда второе уравнение этой системы преобразуется к виду откуда

Здесь для не выполняется условие а для пары не выполняется условие

б) Пусть тогда из системы (1), с учетом условия , получаем , а из второго уравнения следует, что откуда

11 б). Решите систему уравнений:

Решение. Первое уравнение системы можно записать в виде

а множество допустимых значений определяется условием (1)

При выполнении условия (1) исходная система равносильна системе

а система (1)−(2) равносильна совокупности двух систем

Исключая из системы (3), получаем уравнение не имеющее действительных корней. Поэтому система (3) не имеет действительных решений.

Из системы (4) получаем уравнение имеющее корни

Поэтому исходная система имеет два решения:

1. Рассмотрели основные понятия алгебраических систем уравнений, различные методы и способы их решения.

2. Выяснили, в чем состоит процесс решения систем уравнений, определили общие средства перехода к равносильной системе.

3. При решении алгебраических систем уравнений применили как распространенные преобразования и способы, так и другие методы, связывающие новые с традиционными.

Наша школьная математика – это огромный потенциал для использования различных методов и способов для решения нестандартных систем алгебраических уравнений с несколькими переменными, как на уроках, так и на олимпиадах, конкурсах и ЕГЭ.

1. Варианты вступительных экзаменов МФТИ. 1996-2002 г.

2. Учебник-С. М. Никольский, .. 9-10 Кл., 2005-2010 г.

3. В. Н. Дятлов. Этюд №3 Уравнения и системы уравнений. 2013 г.

Решение нестандартных уравнений и систем уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Решение нестандартных уравнений и систем уравнений

1.1. Умножение уравнения на функцию……………………………………5

1.2. Метод неопределённых коэффициентов………………………………7

1.3. Метод введение параметра…………………………………….……….8

1.4. Метод введение новой неизвестной……………………………………8

1.5. Комбинирование различных методов……………………………….…9

1.6. Угадывание корня уравнения…………………………………………10

1.7. Использование суперпозиции функции…………………. …………10

1.8. Раскрытие знаков модулей…………………………….………………11

1.9. Уравнение вида ………………………………..…………12

1.10. Уравнение вида ……………………………………. …13

1.11. Использование свойств абсолютной величины……………………14

1.12. Понижение степени уравнения……………………………………. 15

1.13. Решение некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных……………………….……16

§2. Нестандартные системы уравнений …………………………………….19

Математика занимает одно из главных мест в школьном образовании, она изучается на протяжении всего периода обучения с 1-го по 11-й класс. Школьный курс математики имеет большое значение в системе общеобразовательной подготовки учащихся, формировании у них диалектно-материалистического мировоззрения и готовности к активному участию в сфере материального производства.

Уравнения – это наиболее объёмная тема всего курса математики.

Есть много уравнений, которые считаются для школьников задачами повышенной трудности. Для решения таких задач лучше применять не традиционные методы, а приёмы, которые не совсем привычны для учащихся.

В данной работе систематизирован ряд таких приёмов.

Изучены методы решения уравнений, основанные на геометрических соображениях, свойствах функций, применении производной и др. Кроме этого, в моей работе разобрана масса «хитрых» методов и приёмов решения различных уравнений.

Изучить умножение уравнения на функцию;

Изучить метод неопределённых коэффициентов;

Изучить введение параметра;

Изучить введение новой неизвестной;

Изучить комбинирование различных методов;

Изучить угадывание корня;

Изучить использование суперпозиции функции;

Изучить раскрытие знаков модулей;

Изучить уравнения вида ;

Изучить использование свойств абсолютной величины;

Изучить понижение степени уравнения;

Изучить решения некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных;

Изучить использование графика функции.

§1.Нестандартные уравнения

1.1. Умножение уравнения на функцию

Иногда решение алгебраического уравнения существенно облегчается, если умножить обе его части на некоторую функцию – многочлен от неизвестной. При этом надо помнить, что возможно появление лишних корней – корней многочлена, на который умножили уравнение. Поэтому надо либо умножать на многочлен, не имеющий корней, и получить равносильное уравнение, либо умножать на многочлен, имеющий корни, и тогда каждый из таких корней надо обязательно подставить в исходное уравнение и установить, является ли это число его корнем.

Пример1. Решить уравнение

. (1)

Решение: Умножив обе части уравнения на многочлен , не имеющий корней, получим уравнение

(2)

равносильное уравнению (1). Уравнение (2) можно записать в виде:

(3)

Ясно, что уравнение (3) не имеет действительных корней, поэтому уравнение (1) их не имеет.

Ответ: нет действительных решений.

Пример 2 . Решить уравнение:

(4)

Решение: Умножив обе части уравнения на многочлен , получим уравнение

(5)

являющееся следствием (4), так как уравнение (5) имеет корень , не являющийся корнем уравнения (4).

Уравнение (5) есть симметричное уравнение четвертой степени. Поскольку не является корнем уравнения (5) то, разделив обе части на и перегруппировав его члены, получим уравнение

(6)

равносильное уравнению (5). Обозначив , перепишем уравнение (6) в виде

(7)

уравнение (7) имеет два корня: , . Поэтому уравнение (6) равносильно совокупности уравнений:

Решив каждое из этих уравнений, найдём четыре корня уравнения (6), а тем самым и уравнения (5).

Так как корень является посторонним для уравнения (4), то отсюда получаем, что уравнение (4) имеет три корня.

Ответ:

1.2. Метод неопределенных коэффициентов

Суть этого метода состоит в том, что заранее предполагается вид множителя – многочленов, на которые разлагается данный многочлен, этот метод опирается на следующие утверждения.

два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях ;

любой многочлен третьей степени разлагается в произведение линейного и квадратного множителей;

Любой многочлен четвертой степени разлагается в произведение двух много членов второй степени.

Пример 1 . Разложить на множители многочлен

Решение. Будем искать многочлены и такие, что справедливо тождественное равенство

(1)

Правую часть этого равенства можно записать в виде:

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях равенства (1), получаем систему равенств для нахождения , , , ;

Легко видеть, что этим равенством удовлетворяют числа , , , , а это означает, что многочлен разлагается на множители и .

1.3. Метод введения параметра

Иногда при разложении многочлена на множители помогает метод введения параметра. Суть этого метода хорошо видна в следующем примере.

Пример1 . разложить на множители многочлен

Решение. Рассмотрим многочлен с параметром :

который при превращается в заданный многочлен. Запишем этот многочлен как квадратный трёхчлен относительно :

Так как корни этого квадратного трёхчлена относительно есть и , то справедливо равенство

Следовательно, многочлен разлагается на множители и т.е.

1.4. Метод введения новой переменной

В некоторых случаях путём замены выражения , входящего в многочлен , через , можно получить многочлен относительно , который уже легко разложить на множители. Затем после замены на получаем разложение на множители многочлена .

Пример1. Разложить на множители многочлен

Решение. Преобразуем данный многочлен следующим образом:

Обозначим через . Тогда имеем:

Пример2. Разложить на множители многочлен

Решение. Обозначим через . Тогда

1.5. Комбинирование различных методов

Часто при разложении многочлена на множители приходится применять последовательно несколько из рассмотренных выше методов.

Пример 1. Разложить на множители многочлен

Решение. Применяя группировку, перепишем многочлен в виде:

Применяя к первой скобки метод выделения полного квадрата, имеем:

Наконец, применяя формулу разности квадратов, получим, что

1.6. Угадывание корня уравнения

Иногда внешний вид уравнения подсказывает, какое число является корнем уравнения.

Пример . Решите уравнение

Решение. Очевидно, что есть корень данного уравнения. Для нахождения остальных корней преобразуем многочлен

Так как уравнение не имеет корней, то исходное уравнение имеет единственный корень .

Ответ: .

1.7. Использование суперпозиции функции

Иногда можно найти корень уравнения, если заметить, что функция, находящаяся в одной из частей уравнения, является суперпозицией некоторых более простых функций.

Пример1. Решить уравнение

. (1)

Уравнение (1) можно переписать в виде:

Теперь очевидно, что если – корень уравнения , то и корень уравнения .

Корни уравнения есть и . Отсюда следует, что уравнение (1) имеет эти корни. Переписав уравнение (1) в виде:

(2)

и разделив многочлен (2) на многочлен , получим, что уравнение (2) можно записать в виде:

отсюда следует, что корнями уравнения (1) наряду с и являются также корни уравнения =0 , т.е. числа и .

Ответ: .

1.8. Раскрытие знаков модулей

Основной метод решения уравнений, содержащих модули, состоит в следующем: надо разбить ОДЗ уравнения на множества, на каждом из которых каждое из выражений, находящихся под знаком модуля, сохраняет знак. На каждом таком множестве уравнение записывается без знака модуля и затем решается на этом множестве. Объединение решений, найденных на всех этих множествах – частях ОДЗ уравнения, составляет множество всех его решений.

Пример1. Решить уравнение

. (1)

Решение. ОДЗ уравнения состоит из всех действительных . Разобьём ОДЗ на два промежутка:

А) ,

Б) .

А) Пусть тогда и уравнение (1) запишется на этом множестве так:

Это уравнение превращается в верное числовое равенство для любого действительного , т.е. его решениями являются все действительные . Из них условию удовлетворяют все из промежутка . Они и являются решениями уравнения (1) в случае А).

Б) Пусть , тогда и уравнение (1) запишется на этом множестве так:

. (2)

Решение этого уравнения есть , , Из этих значений условию удовлетворяют только , . Итак, решения уравнения (1) есть , и все из промежутка .

Ответ: .

1.9. Уравнения вида

(1)

можно решать основным методом. Однако в некоторых случаях полезно уравнение (1) решать следующим образом:

Найти ту часть ОДЗ уравнение (1), где ;

На этой области уравнение (1) равносильно совокупности двух уравнений

Решение этой совокупности, принадлежащие рассматриваемой области, и дадут решение уравнения (1).

Пример1. Решите уравнение

. (2)

Решение. ОДЗ этого уравнения есть все действительные . Очевидно, что на ОДЗ, т.е. для любого ,

Поэтому уравнение (2) равносильно совокупности уравнений

Убедимся, что первое уравнение решений не имеет.

Второе уравнение системы равносильно уравнению .

Ответ : .

1.10. Уравнение вида

(1)

можно решить согласно общему методу. Однако иногда бывает полезно заменить уравнение (1) уравнением , т.е. равносильное ему на его ОДЗ уравнением

Пример1: Решите уравнение

. (2)

Решение: ОДЗ уравнения (2) есть все действительные , возведя обе части уравнения в квадрат, получим уравнение

равносильное исходному. Это уравнение можно переписать в виде:

Оно равносильно совокупности уравнений:

Так как и дискриминант квадратного трехчлена отрицателен, то первое уравнение последней совокупности имеет единственный корень .

то решения второго уравнения совокупности есть , , .

Итак, исходное уравнение имеет четыре корня: , , , .

Ответ: .

1.11. Использование свойств абсолютной величины

При решении уравнений с модулем иногда бывает полезно решать их не основным методом, а применять различные свойства абсолютных величин действительных чисел.

Пример1: Решите уравнение

(1)

Решение: Обозначим через и через . Тогда уравнение (1) можно записать в виде:

. (2)

Из свойств абсолютной величины вытекает, что равенство (2) возможно тогда и только тогда, когда одновременно, и . Поэтому исходное уравнение (1) равносильно системе неравенств.

Решение этой системы неравенств, а значит, и исходного уравнения есть .

Ответ: .

1.12. Понижение степени уравнения

Некоторые алгебраические уравнения заменой в них некоторого многочлена одной буквой могут быть сведены к алгебраическим уравнениям, степень которых меньше степени исходного уравнения и решение которых проще.

Пример1: Решите уравнение

. (1)

Решение: Обозначим , тогда уравнение (1) можно переписать в виде . Последние уравнение имеет корни и . Следовательно, уравнение (1) равносильно совокупности уравнений

Решение первого уравнения этой совокупности есть , . Решения второго уравнения есть , . Решениями уравнения (1) являются , , , .

Ответ: .

Пример2: Решить уравнение

(2)

Решение: Умножив обе части уравнения на и обозначив , , получим уравнение

Переписав это уравнение в виде:

(3)

и обозначив , перепишем уравнение (3) в виде:

Последние уравнение имеет корни и . Поэтому получаем, что уравнение (3) равносильно совокупности двух уравнений

Решение этой совокупности уравнений есть и , т.е. уравнение (2) равносильно совокупности уравнений

(4)

Решение совокупности (4) являются и _, они и являются решениями уравнения (2).

Ответ: .

1.13. Решение некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных

Решение уравнений сведением их к решению систем уравнений относительно новых неизвестных проиллюстрирую в примерах.

Пример1: Решить уравнение

(1)

Решение. Пусть – решение уравнения (1).

Введем новую неизвестную

Тогда для нахождения и имеем систему уравнений

(2)

Поскольку , то вводя новые неизвестные

, , систему (2) можно переписать в виде:

Решение этой системы есть пары чисел ,,, , откуда для нахождения x ₀ и у ₀ получаем системы уравнений:

Решение первой из этих систем есть , и , . Вторая система решений не имеет.

Итак, все решения уравнения (1) содержатся среди чисел и .

Проверка показывает, что эти числа являются решениями уравнения (1).

Ответ: .

Пример2: Решить уравнение

. (3)

Решение: Пусть – решение уравнения (3).

Введем новую неизвестную , тогда и являются решением системы уравнений

(4)

Вводя новые неизвестные , , перепишем систему (4) в виде:

(5)

Решения системы (5) есть , . Д ля нахождения и получим систему уравнений

Эта система имеет две пары решений: и .

Итак, все решения уравнения (3) содержатся среди чисел и . Проверка показывает, что оба эти числа являются корнями уравнения (3).

Ответ: .

Пример3: Решить уравнение

. (6)

Решение: Пусть – решение уравнения (6).

Введем новые неизвестные:

= u , = v .

Тогда и являются решениями системы уравнений

Эта система равносильна системе

(7)

Решения системы (7) есть ,; , , а это означает, что решениями уравнения (6) могут быть только число и . Проверка показывает, что эти числа являются решениями уравнения (6).

Ответ: .

§2. Нестандартные системы уравнений

В этом параграфе приведены примеры систем уравнений, для решения которых приходится использовать особые приемы.

(1)

Решение: Выполним некоторые преобразования первого уравнения системы:

Это уравнение равносильно системе уравнений

(2)

Уравнение сводится к совокупности уравнений:

В первом случае , во втором . Значит, система (2) равносильна совокупности двух систем:

Из первой системы находим

(3)

Из второй системы находим

(4)

(5)

Пары, задаваемые условиями (3), (4), (5) – решения системы (2). Воспользовавшись теперь тем, что , получаем решения системы (1):

Ответ:

Пример2: Найти все решения системы уравнений.

удовлетворяющие условию .

Решение: рассмотрим последнее уравнение как, квадратное уравнение относительно переменной : . Это уравнение разрешимо тогда и только тогда, когда его . С учетом условия , получаем условие .