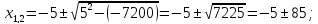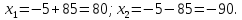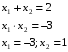Нестандартные способы решения квадратных уравнений проект

Учебный проект «Нестандартные приемы решения квадратных уравнений»

Разделы: Математика

Тема «Квадратные уравнения» является одной из самых актуальных. Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение в разных разделах математики.

В школьном курсе изучаются формулы корней квадратного уравнения, с помощью которых можно решать любые квадратные уравнения. Однако, имеются и другие приемы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать квадратные уравнения?

Гипотеза: установление связи между коэффициентами и корнями квадратного уравнения позволит найти эффективные приемы быстрого решения квадратного уравнения.

Цель: установив связь между коэффициентами и корнями квадратного уравнения, найти новые рациональные приемы решения уравнений

• Изучить литературу по истории приемов решения квадратных уравнений
• Обобщить накопленные знания о квадратных уравнениях и способах их решения.
• Установить зависимость корней квадратного уравнения от его коэффициентов и найти эффективные приемы быстрого решения квадратного уравнения, в том числе с большими коэффициентами.
• Сделать выводы.
• Разработать дидактический материал для проведения практикума по решению квадратных уравнений с использованием новых приемов в помощь ученикам, увлеченным математикой и учителям, ведущим факультативные занятия.

Объект исследования: квадратные уравнения

Предмет изучения: методы и приемы решения квадратных уравнений, в том числе с большими коэффициентами

Глава 1.
Изучение литературы

Основной материал, связанный с изучением темы «Квадратные уравнения» находится в УМК под ред.С.А.Теляковского. В учебнике разобраны все основные вопросы по теме:

1. Определение и виды квадратных уравнений

2. Основные методы решения квадратных уравнений

Однако, дополнительный материал, связанный с историей вопроса о возникновении квадратных уравнений можно найти в «Энциклопедия по математике» «Занимательная математика», М., 2007. Способы решения задач на квадратные уравнения в полном объёме раскрыты в изданиях «Сборник элективных курсов» Волгоград, 2006 г.

Изученная литература позволила приобрести новые интересные знания по истории возникновения квадратного уравнения, приобрести опыт по решению различных квадратных уравнений и перейти к следующему этапу в исследовании – перенести полученные знания в нестандартную ситуацию.

Глава 2.
Изучение истории вопроса о квадратных уравнениях

Глава 3.
Обобщение имеющихся знаний о квадратных уравнениях и способах их решения

Глава 4.
Нестандартные приемы решения квадратных уравнений

Дидактический материал по применению нестандартных приемов решения квадратных уравнений.

1. Найди наиболее рациональным способом корни уравнения:

1978х 2 – 1984х + 6=0
(1; 6/1978)

4х 2 + 11х + 7 = 0
(-1; -7/4)

319х 2 + 1988х +1669=0
(-1; -1669/319)

2. Решить квадратные уравнения с большими коэффициентами

839х 2 – 448х -391=0
(1; -391/839)

345х 2 – 137х – 208=0
(1;.-208/345)

3. Используя полученные знания, установи соответствие:

1) х 2 +5х+6=0 2) 6х 2 -5х+1=0 3) 2х 2 -5х+3=0 4) 3х 2 -5х+2=0 5) х 2 -5х+6=0 6) 6х 2 +5х+1=0 7) 2х 2 +5х+2=0 8) 3х 2 +5х+2=0

1) 1/6;1/2 2) 1; 3/2 3) 1; 2/3 4) -2; -3 5) -1/3 ; -1/2 6) -1; -3/2 7) -1; -2/3 8) 2;3

Глава 5.
Анализ работы учащихся по решению квадратных уравнений нестандартными способами

Разработаны критерии оценки проведенного практикума:

1. За каждое верно выполненное задание ставится 1 балл;
2. Наиболее возможное количество набранных баллов-17
3. Если ученик набирает менее

7 баллов, то выставляется оценка «2»
от 7 до 11 баллов «3»
от 12 до 15 баллов «4»
от 16-17 баллов «5»

Выполняли работу – 11человек

от 16-17 – 5человек (45%)
от 12-15– 6человек (55%)
Менее 12 – 0 человек

Средний балл – 4,45

Процент качества – 100%

Типичные ошибки, допущенные в работе связаны с невнимательностью учащихся.

Выводы по результатам проведения практикума

Успешно выполненная работа учащимися 8 класса, позволяет сделать следующие выводы:

• нестандартные приемы решения квадратных уравнений заслуживают внимания;
• позволяют экономить время решения, что обусловлено применением тестовой системы экзаменов.

В процессе работы над проектом, была создана система нестандартных приемов решения квадратных уравнений и разработан банк заданий, на основе которого проведена успешная апробация этих приемов.

Данный материал можно рекомендовать для внеклассных и факультативных занятий по математике. Учителя могут использовать его как методическое пособие при изучении темы «Решение квадратных уравнений», а также, для контроля за знаниями учащихся.

Материалом этого проекта могут воспользоваться и те, кто любит математику и хочет знать о математике больше.

1. Выгодский М.Я. Справочник по элементарной математике. – М. государственное издательство физико-математической литературы, 1970.
2. Галицкий М.Л., Гольдман М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов: учебное пособие для учащихся школ и классов с углубленным изучением математики:4-е изд.-М.: Просвещение, 1997.
3. Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Учебник для 8 класса. М., Просвещение, 2001.
4. Макарычев Ю.Н., Миндюк Н.Г. Дополнительные главы к школьному учебнику. 8 класс М., Просвещение, 1996.
5. Штейнгауз В.Г. Математический калейдоскоп. – М.: Бюро «Квантум», 2005.
6. Энциклопедический словарь юного математика. – М.: Педагогика, 1985.

Нестандартные способы решения квадратных уравнений проект

Главная
• Список секций
• Математика
• Нестандартные способы решения квадратных уравнений

Нестандартные способы решения квадратных уравнений

Автор работы награжден дипломом победителя III степени

Введение

Математическое образование, получаемое в школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений.

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям.

Актуальность темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, это также может мне пригодится при решении более сложных задач, в том числе в 9 классе, а также 10 и 11 и при сдаче экзаменов.

Цель: Изучить стандартные и нестандартные способы решения квадратных уравнений

Задачи

1. Изложить наиболее известные способы решения уравнений
2. Изложить нестандартные способы решения уравнений
3. Сделать вывод

Объект исследования: квадратные уравнения

Предмет исследования: способы решения квадратных уравнений

Методы исследования:

• Теоретические: изучение литературы по теме исследования;
• Анализ: информации полученной при изучении литературы; результатов полученных при решении квадратных уравнений различными способами.
• Сравнение способов на рациональность их использования при решении квадратных уравнений.

Глава 1.Квадратные уравнения и стандартные способы решения

1.1.Определение квадратного уравнения

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0, где х – переменная, а, b и с– некоторые числа, причем, а ≠ 0.

Числа а, b и с — коэффициенты квадратного уравнения. Число а называют первым коэффициентом, число b– вторым коэффициентом и число c – свободным членом.

Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых т.е. коэффициенты в и с отличны от нуля.

Неполное квадратное уравнение — это уравнение, в котором хотя бы один из коэффициентов в или, с равен нулю.

Определение 3. Корнем квадратного уравнения ах 2 + bх + с = 0 называют всякое значение переменной х, при котором квадратный трехчлен ах 2 + bх + с обращается в нуль.

Определение 4. Решить квадратное уравнение — значит найти все его

корни или установить, что корней нет.

Пример: – 7x + 3 =0

В каждом из уравнений вида a + bx + c = 0, где а ≠ 0, наибольшая степень переменной x – квадрат. Отсюда и название: квадратное уравнение.

Квадратное уравнение, в котором коэффициент при х2 равен 1, называют приведенным квадратным уравнением.

Пример

1.2.Стандартные способы решения квадратных уравнений

Решение квадратных уравнений с помощью выделения квадрата двучлена

Решение квадратного уравнения, в котором оба коэффициента при неизвестных и свободный член отличны от нуля. Такой способ решения квадратного уравнения называют выделением квадрата двучлена.

Разложение левой части уравнения на множители.

Решим уравнение х 2 + 10х — 24 = 0. Разложим левую часть на множители:

х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).

Следовательно, уравнение можно переписать так:(х + 12)(х — 2) = 0

Произведение множителей равно нулю, если по крайней мере, один из его множителей равен нулю.

Решение квадратного уравнения по формуле.

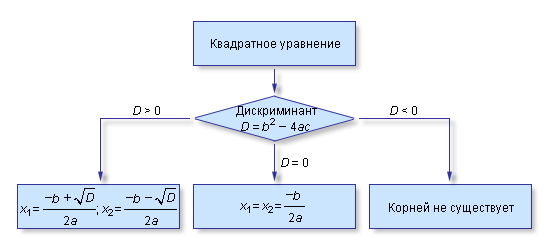
Дискриминант квадратного уравнения ax 2 + bx + c = 0 выражение b 2 – 4ас = D — по знаку которого судят о наличии у этого уравнения действительных корней.

Возможные случаи в зависимости от значения D:

1. Если D>0, то уравнение имеет два корня.
2. Если D= 0, то уравнение имеет один корень: х =
3. Если D 2 + bx + c = 0.

Обозначим второй коэффициент буквой р, а свободный член буквой q:

х 2 + px + q = 0, тогда

Глава 2.Нестандартные способы решения квадратных уравнений

2.1.Решение с помощью свойств коэффициентов квадратного уравнения

Свойства коэффициентов квадратного уравнения – это такой способ решения квадратных уравнений, который поможет быстро и устно найти корни уравнения:

1. Еслиа+ b+c=0, тоx₁= 1,x₂=

Пример. Рассмотрим уравнение х 2 +3х – 4= 0.

Проверим полученные корни с помощью нахождения дискриминанта:

Следовательно, если + b +c= 0, то x₁ = 1, x₂ =

1. Еслиb =a+c, тоx₁= -1,x₂=

Пример. Рассмотрим уравнение 3х 2 +4х +1 = 0, a=3, b=4, c=1

Значит корнями этого уравнения являются –1 и . Проверим это с помощью нахождения дискриминанта:

D= b 2 – 4ас=4 2 – 4·3·1 = 16 – 12 = 4

2.2.Способ «переброски»

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а±b+c≠0, то используется прием переброски:

Применяя способ «переброски» получаем:

Таким образом, с помощью теоремы Виета получаем корни уравнения:

Однако корни уравнения необходимо поделить на 3 (то число, которое «перебрасывали»):

Значит, получаем корни: x₁ = -1, x₂ = .

2.3.Решение с помощью закономерности коэффициентов

1. Если уравнениеax 2 + bx + c= 0, коэффициентb= (a2+1), и коэффициентc=a, то его корни равны x₁ = —a, x₂ =

Таким образом, решаемое уравнение должно иметь вид

Пример. Рассмотрим уравнение 3х 2 +10х +3 = 0.

Таким образом, корни уравнения: x₁ = -3, x₂ =

Проверим данное решение с помощью дискриминанта:

D= b 2 – 4ас=10 2 – 4·3·3 = 100 – 36 = 64

1. Если уравнениеax 2 — bx + c= 0, коэффициентb= (a2+1), и коэффициентc=a, то его корни равны x₁ = a, x₂ =

Таким образом, решаемое уравнение должно иметь вид

Пример. Рассмотрим уравнение 3х 2 — 10х +3 = 0.

Таким образом, корни уравнения: x₁ = 3, x₂ =

Проверим данное решение с помощью дискриминанта:

D= b 2 – 4ас=10 2 – 4·3·3 = 100 – 36 = 64

1. Если уравнениеax 2 + bx — c= 0, коэффициентb= (a2-1), и коэффициентc=a, то его корни равны x₁ = —a, x₂ =

Таким образом, решаемое уравнение должно иметь вид

Пример. Рассмотрим уравнение 3х 2 + 8х —3 = 0..

Проверим данное решение с помощью дискриминанта:

D= b 2 – 4ас=8 2 + 4·3·3 = 64 + 36 = 100

1. Если уравнениеax 2 — bx — c= 0, коэффициентb= (a2-1), и коэффициентc=a, то его корни равны x₁ = a, x₂ =

Таким образом, решаемое уравнение должно иметь вид

Пример. Рассмотрим уравнение 3х 2 — 8х —3 = 0..

Таким образом, корни уравнения: x₁ = 3, x₂ = —

Проверим данное решение с помощью дискриминанта:

D= b 2 – 4ас=8 2 + 4·3·3 = 64 + 36 = 100

2.4.Решение с помощью циркуля и линейки

Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + bх + с = 0 с помощью циркуля и линейки (рис.6 ).

Допустим, что искомая окружность пересекает ось

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому

1) построим точки S (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис.8б) в точке В(х₁; 0), где х₁ — корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра AS SB, R> б) AS=SB, R= в) AS 2 — 2х — 3 = 0 (рис.8).

Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA, где А (0; 1).

2.5.Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

Примеры.

1) Решим уравнение х 2 + 10х = 39.

В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.9).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей:

первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х 2 + 10х + 25. Заменяя

х 2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим:

2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0.

Решение представлено на рис 10. где

у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.

Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой

один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у₁ = 2, у₂ = — 8 (рис. .

3) Решить геометрически уравнение у 2 — 6у — 16 = 0.

Преобразуя уравнение, получаем

На рис 11. находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у 2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у 2 — 6у равным ему числом 16,

получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у₁ = 8 и у₂ = — 2.

Заключение

В ходе выполнения своей исследовательской работы я считаю, что с поставленной целью и задачами я справился, мне удалось обобщить и систематизировать изученный материал по выше указанной теме.

Нужно отметить, что каждый способ решения квадратных уравнений по-своему уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на контрольных работах и экзаменах. При работе над темой я ставил задачу, выяснить какие методы являются стандартными, а какие нестандартными.

Итак, стандартные методы (используются чаще при решении квадратных уравнений):

• Решение с помощью выделения квадрата двучлена
• Разложение левой части на множители
• Решение квадратных уравнений по формуле
• Решение с помощью теоремы Виета
• Графическое решение уравнений

Нестандартные методы:

• Свойства коэффициентов квадратного уравнения
• Решение способом переброски коэффициентов
• Решение с помощью закономерности коэффициентов
• Решение квадратных уравнений, с помощью циркуля и линейки.
• Исследование уравнения на промежутках действительной оси
• Геометрический способ

При этом следует заметить, что каждый способ обладает своими особенностями и границами применения.

Решение уравнений с использованием теоремы Виета

Достаточно легкий способ, дает возможность сразу увидеть корни уравнения, при этом легко находятся только целые корни.

Решение уравнений способом переброски

За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета, при этом также легко найти только целые корни.

Свойства коэффициентов квадратного уравнения

Доступный метод для устного нахождения корней квадратного уравнения, но подходит только к некоторым уравнениям

Графическое решение квадратного уравнения

Наглядный способ решения квадратного уравнения, однако могут возникать погрешности при составлении графиков

Решение квадратных уравнений с помощью циркуля и линейки

Наглядный способ решения квадратного уравнения, но также могут возникать погрешности

Геометрический способ решения квадратных уравнений

Наглядный способ, похож на способ выделения полного квадрата

Решая уравнения разными способами, я пришел к выводу, что зная комплекс методов решения квадратных уравнений, можно решить любое уравнение, предлагаемое в процессе обучения.

При этом, следует заметить, что одним из более рациональных способов решения квадратных уравнений является способ «переброски» коэффициента. Однако самым универсальным способом можно считать стандартный способ решения уравнений по формуле, потому что данный способ позволяет решить любое квадратное уравнение, хотя иногда и за более длительное время. Также такие способы решения, как способ «переброски», свойство коэффициентов и теорема Виета помогаю сэкономить время, что очень важно при решении заданий на экзаменах и контрольных работах.

Думаю, что моя работа будет интересна учащимся 9-11 классов, а также тем, которые хотят научиться решать рационально квадратные уравнения и хорошо подготовиться к выпускным экзаменам. Также она будет интересна и учителям математики, за счет рассмотрения истории квадратных уравнений и систематизации способов их решения.

Список литературы

1. Глейзер, Г.И. История математики в школе/ Г.И. Глейзер.-М.: Просвещение, 1982- 340с.
2. Гусев, В.А. Математика. Справочные материалы/ В.А. Гусев, А.Г. Мордкович — М.: Просвещение, 1988, 372с.
3. Ковалева Г. И., Конкина Е. В. «Функциональный метод решения уравнений и неравенств», 2014 г.
4. Кулагин Е. Д. «300 конкурсных задач по математике», 2013 г.
5. Потапов М. К. «Уравнения и неравенства. Нестандартные методы решения» М. «Дрофа», 2012 г.
6. .Барвенов С. А «Методы решения алгебраических уравнений», М. «Аверсэв», 2006 г.
7. Супрун В.П. «Нестандартные методы решения задач по математике» — Минск «Полымя», 2010г
8. Шабунин М.И. «Пособие по математике для поступающих в вузы», 2005г.
9. Башмаков М.И. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 287с.
10. Шаталова С. Урок – практикум по теме «Квадратные уравнения».- 2004.

Нестандартные способы решения квадратных уравнений

Одно из важных мест в математике занимают уравнения, так как большинство жизненных задач сводится к решению различных видов уравнений, и чаще всего это уравнения квадратного вида.

Просмотр содержимого документа
«Нестандартные способы решения квадратных уравнений»

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Кемеровский государственный университет»

Институт профессиональной ориентации

VI Областная научно-практическая конференция «ДИАЛОГ»

НЕСТАНДАРТНЫЕ СПОСОБЫ РЕШЕНИЯ

Автор: Шмидт Нелли

МБОУ «Гимназия №12»

Слотюк Мария Викторовна

Глава 1. История развития квадратных уравнений 5

Глава 2. Стандартные способы решения квадратных уравнений

2.1. Решение квадратного уравнения по формулам 6

2.2. Решение уравнений с четным коэффициентом при х 7

2.3. Теорема Виета 7

Глава 3. Нестандартные способы решения квадратных уравнений

3.1. Метод выделения полного квадрата 8

3.2. Графическое решение квадратных уравнений 9

3.3. Разложение левой части уравнения на множители 10

3.4. Решение уравнений способом «переброски» 10

3.5. Решение уравнений по сумме коэффициентов 11

3.6. Квадратное уравнение с целыми коэффициентами 11

3.7. Закономерность коэффициентов 12

Математика является одним из основных и достаточно сложных предметов школы. Она помогает в изучении других дисциплин естественнонаучного цикла, таких как физика, химия, информатика и т.д. При обучении математики развивается логическое мышление, которое также способствует усвоению предметов гуманитарного цикла.

При обучении математике формируются умения и навыки умственного труда, такие как: четкое планирование своей работы, поиск рациональных путей, критическая оценка результатов. Во время обучения математике необходимо излагать свои мысли ясно, лаконично, математические записи выполнять, аккуратно и грамотно. Практические умения и навыки, приобретаемые на уроках математики, пригодятся также для трудовой и профессиональной подготовки.

Одно из важных мест в математике занимают уравнения, так как большинство жизненных задач сводится к решению различных видов уравнений, и чаще всего это уравнения квадратного вида.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые не отражены в школьных учебниках математики. Но мы считаем, что применение разнообразных способов решения поможет сэкономить время и значительно повысить эффективность и качество решения квадратных уравнений.

В некоторых случаях уравнения можно решать устно, но для этого необходимо знать алгоритм решения квадратных уравнений, который так же может пригодиться на экзаменах ОГЭ, ЕГЭ и в различных жизненных ситуациях.

Таким образом, возникает необходимость изучения этих дополнительных и нестандартных способов решения. Все сказанное выше доказывает актуальность темы нашего исследования «Нестандартные способы решения квадратных уравнений»

изучение нестандартных способов решения квадратных уравнений, не входящих в школьный курс математики.

Изучить историю развития квадратных уравнений.

Проанализировать учебники алгебры за 8 класс разных авторов для выявления способов решения квадратных уравнений.

Изучить нестандартные способы решения квадратных уравнений.

Выяснить способы решения квадратных уравнений, которыми владеют учащиеся Гимназии, в результате опроса.

Объект исследования: квадратные уравнения.

Предмет исследования: нестандартные способы решения квадратных уравнений.

• анализ научно – популярной литературы;

• статистические методы обработки данных.

Материалом для исследования послужили учебники «Алгебра 8» следующих авторов: А.Г. Мордкович, Г.В. Дорофеев, С.М. Никольский, Ю.Н. Макарычев, Ш.А. Алимов, Н.Я. Виленкин, А.Г. Мерзляк, Г.К. Муравин; а также различные интернет-ресурсы.

Глава 1. История развития квадратных уравнений

Необходимость в решении уравнений была вызвана ещё до нашей эры потребностью решать задачи, связанные с нахождением площади земельного участка, с земляными работами военного характера, а также с развитием астрономии, да и самой математики.

Некоторые приемы решения квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, как дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты представляют собой задачи с решениями, записанные в виде рецептов, без указаний каким образом они были найдены. [8]

Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид, живший в III веке до н. э — отвел геометрической алгебре в своем трактате «Начала» всю вторую книгу, где собрал весь необходимый материал для решения квадратных уравнений.

Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский (III в.). Однако, способ решение полных квадратных уравнений Диофант изложил в книгах, которые, к сожалению, не сохранились.

Индийский ученый – Брахмагупта (VII в.) изложил общее правило решения квадратных уравнений, которое по существу совпадает с современным. [9]

Аль – Хорезми — арабский учёный, который в 825 г. написал книгу «Книга о восстановлении и противопоставлении». Это был первый в мире учебник алгебры, в котором Хорезми насчитывает 6 видов уравнений.

Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. итальянским математиком Леонардом Фибоначчи. Выводом формулы решения квадратных уравнений общего вида занимался Франсуа Виет, однако он признавал только положительные корни. Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591 г. После трудов нидерландского математика А. Жирара (1595 — 1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.

В настоящее время умение решать квадратные уравнения необходимо для всех. Так как, во-первых, умение быстро, рационально и правильно решать квадратные уравнения облегчает прохождение многих тем курса математики, а во-вторых, большинство практических задач реального мира тоже сводится к решению квадратных уравнений.

Глава 2. Стандартные способы решения квадратных уравнений

2.1. Решение квадратного уравнения по формулам

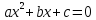
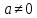
Квадратным уравнением называют уравнение вида , где a, b, c – любые действительные числа, причем . Квадратное уравнение называют приведенным, если его старший коэффициент равен 1. Также различают полные и неполные квадратные уравнения. В нашей работе мы рассматриваем способы решения только полных уравнений.

Рис. 1. Решение по формулам квадратного уравнения

Самый распространенный способ решения квадратных уравнений,

который рассматривается в каждом учебнике алгебры, это решение по формулам. На нем мы подробно останавливаться не будем.

2.2. Решение уравнений с четным коэффициентом при х

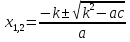
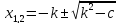
Если коэффициент b есть четное число, то формулу можно упростить, подставив 2k вместо b. Тогда корни квадратного уравнения ax 2 +2kx+c=0 можно вычислять по формуле: , которая значительно облегчает вычисления. А для приведенного квадратного уравнения эта формула выглядит еще проще: . [6]

Решим уравнение: х 2 +10х-7200=0.

Данный способ решения квадратных уравнений с четным вторым коэффициентом рассматривается во всех учебниках алгебры, но только у А.Г. Мордковича и Г.В. Дорофеева выделен отдельным пунктом.

2.3. Теорема Виета

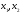
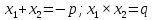
Если — корни уравнения х² + pх + q = 0, то справедливы формулы: .

То есть сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Решим уравнение: х² — 2х – 3 =0

По коэффициентам p и q можно предсказать знаки корней:

а) Если сводный член q 0, то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р , то оба корня отрицательны, если р , то оба корня положительны.

б) Если свободный член q , то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p 0 .

Решение квадратных уравнений по теореме Виета, так же как и решение по формулам, изучается во всех рассмотренных нами учебниках алгебры. Это достаточно легкий способ. Он позволяет сразу увидеть корни уравнения, но найти можно только целые корни.

Глава 3. Нестандартные способы решения квадратных уравнений

3.1. Метод выделения полного квадрата

Решим квадратное уравнение: х² — 2х – 3=0.

Преобразуем это уравнение таким образом:

х² — 2х = 3, х² — 2х +1= 3+1, (х — 1)² = 4.

Следовательно: х – 1 = 2 или х — 1 = -2, откуда х₁ = 3, х₂ = -1.

Решая уравнение, мы преобразовали его так, что в левой части получился квадрат двучлена, а правая часть не содержит неизвестное. В нашем случае уравнение имеет два корня, но если после выделения квадрата двучлена справа получится ноль, то корень будет один, а если отрицательное число окажется справа – корней нет. Данный метод позволяет за минимальное количество действий найти корни уравнения. Однако есть и определенные неудобства, нужно суметь правильно найти все слагаемые для выделения полного квадрата. Этот метод подробно рассматривается в учебниках алгебры Ш.А. Алимова, Г.К. Муравина и Ю.Н. Макарычева, но упражнений на его применение очень мало.

3.2. Графическое решение квадратных уравнений

Решим уравнение .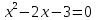

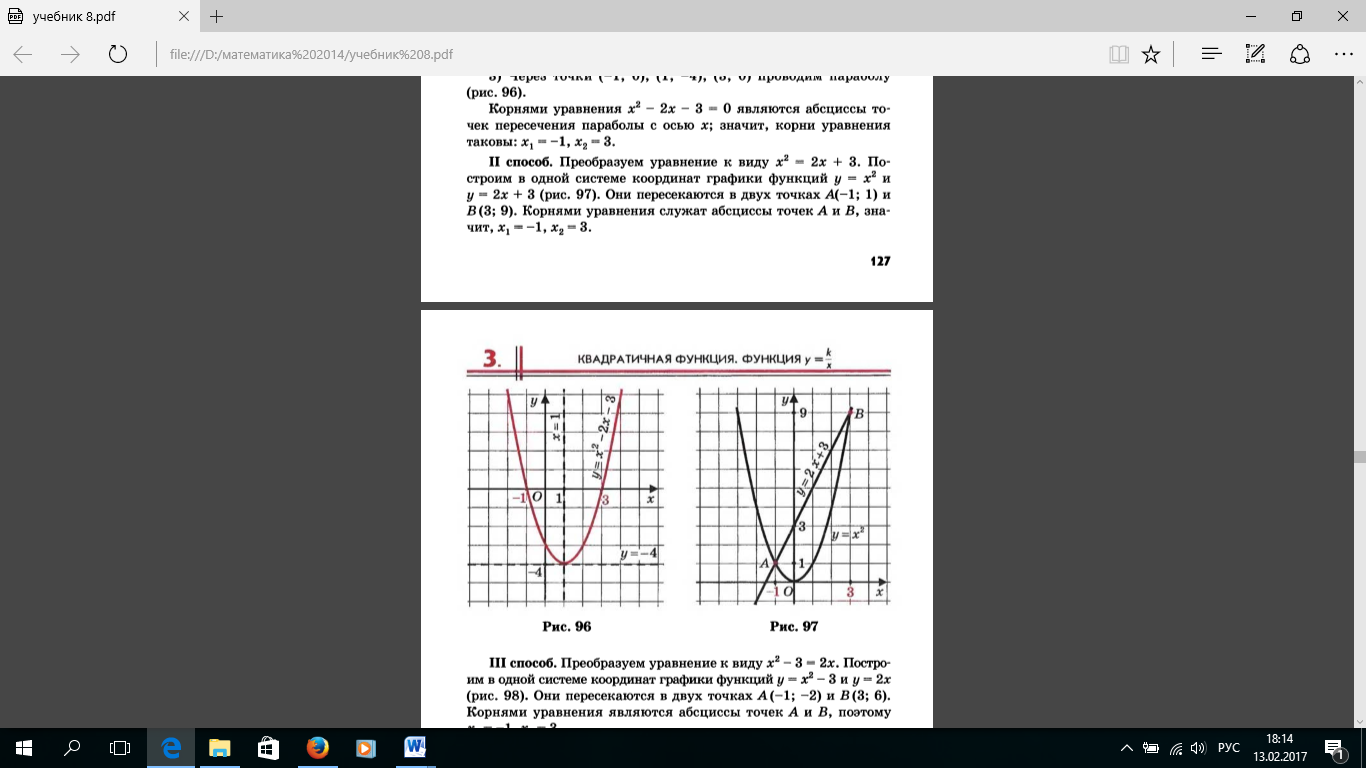
1 способ. Построим график функции

. Вершиной параболы служит точка (1;-4), а осью параболы – прямая х=1. Корнями уравнения являются абсциссы точек пересечения параболы с осью х, корни уравнения: -1 и 3. (Рис. 2)

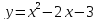
2 способ. Преобразуем уравнение к виду

. Построим в одной системе координат графики функций . Они пересекаются в двух точках (-1;1) и (3;9). Корнями уравнения служат абсциссы этих точек: -1 и 3. (Рис. 3)

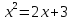
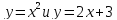
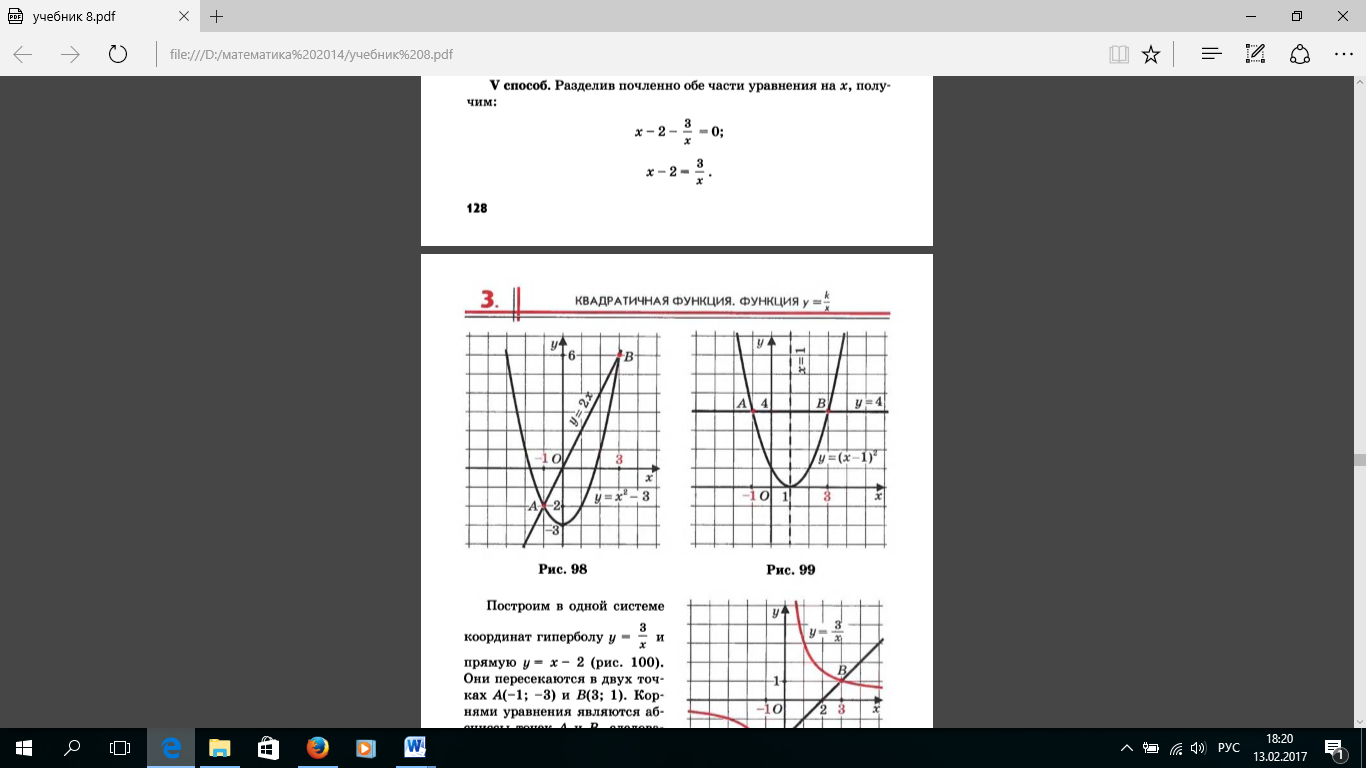
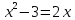
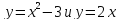
3 способ. Преобразуем уравнение к виду . Построим в одной системе координат графики функций . Они пересекаются в двух точках (-1;1) и (3;9). Корнями уравнения служат абсциссы этих точек: -1 и 3. (Рис. 4)

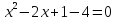
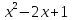
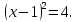
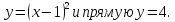
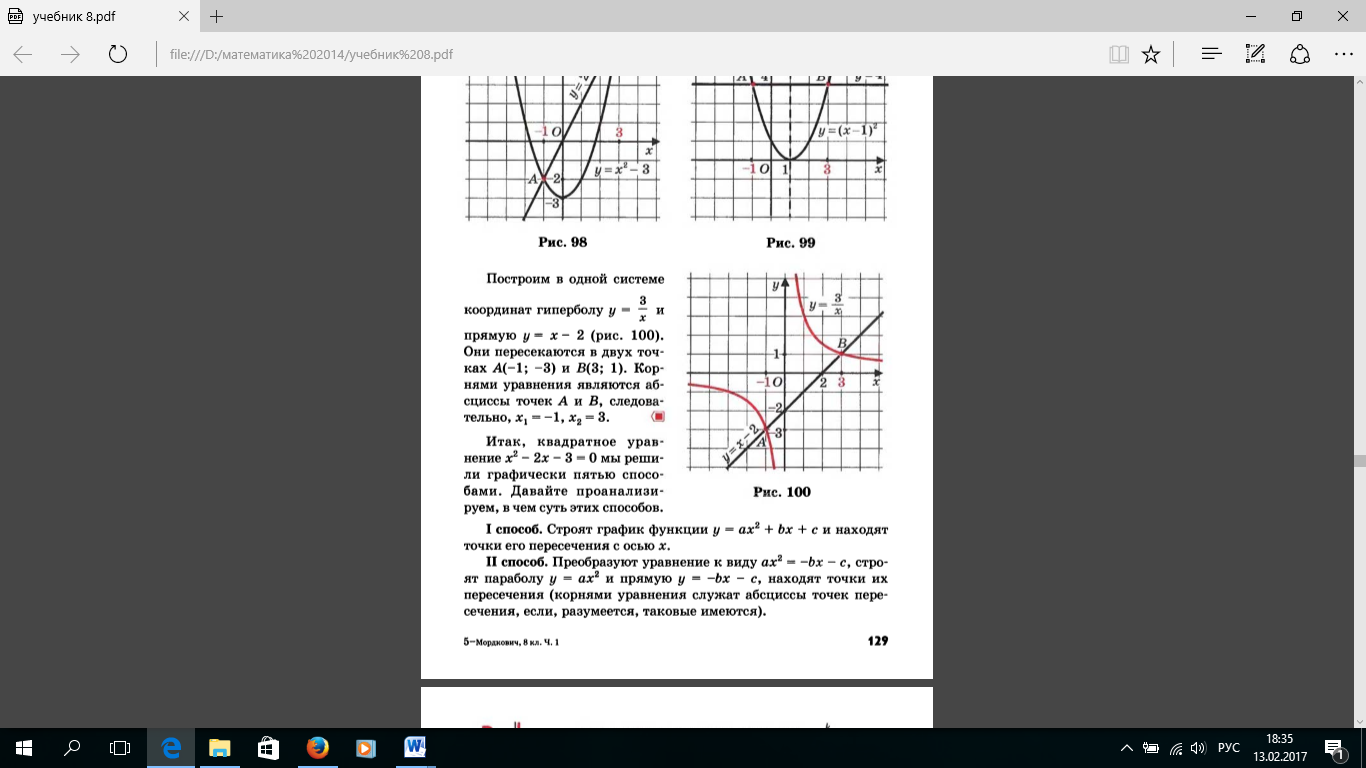
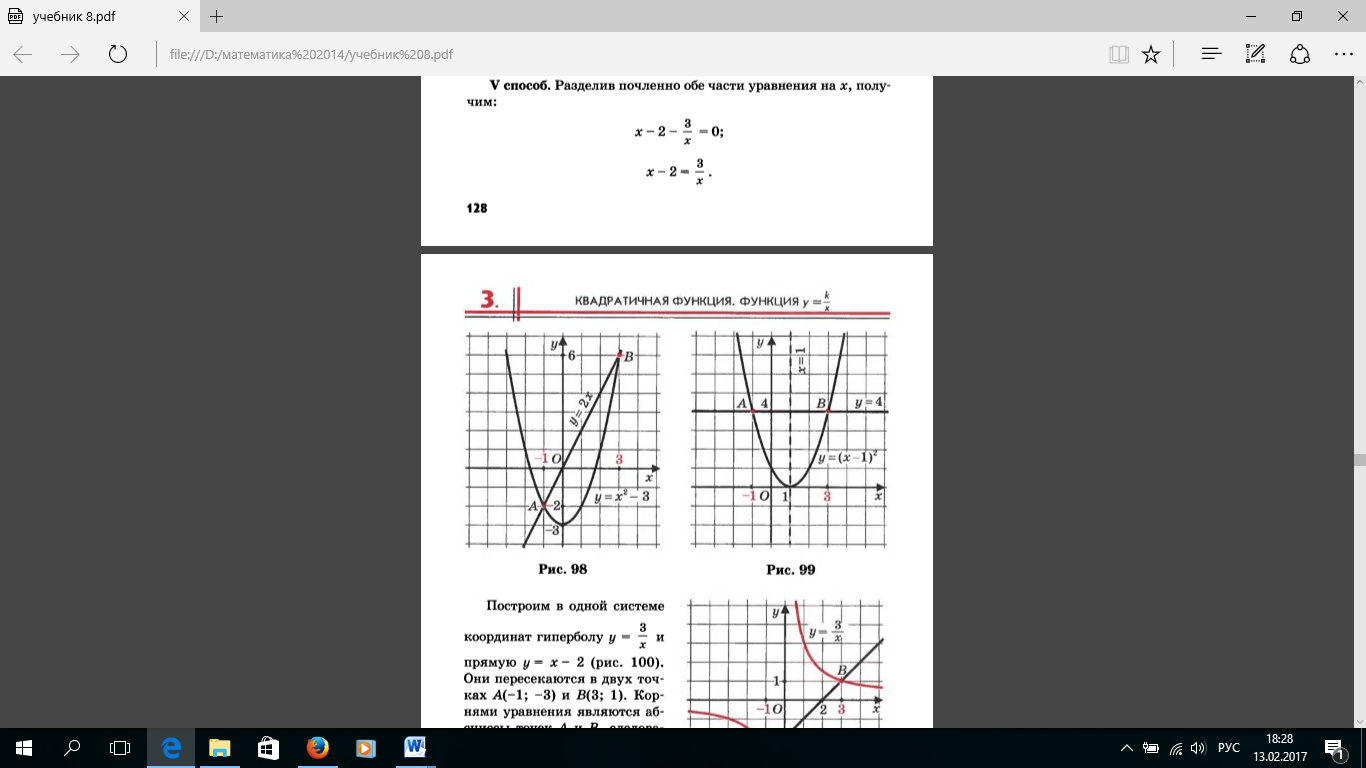
4 способ. Преобразуем уравнение к виду и далее =4, т.е. Построим в одной системе координат параболуОни пересекаются в двух точках (-1;1) и (3;9). Корнями уравнения служат абсциссы этих точек: -1 и 3. (Рис.5)

5 способ. Разделив почленно обе части уравнения на х, получим: 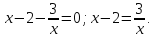Построим в одной системе координат гиперболу у = и прямую у = х – 2. Они пересекаются в двух точках (-1;1) и (3;9). Корнями уравнения служат абсциссы этих точек: -1 и 3. (Рис. 6) [6]

Графический способ решения квадратных уравнений очень подробно рассматривается в учебнике, автором которого является А. Г. Мордкович. Но, несмотря на обилие способов графического решения, уверенности в том, что любое квадратное уравнение мы сможем решить графически, нет. И не всегда точки пересечения имеют «хорошие» координаты.

3.3. Разложение левой части уравнения на множители

Решим уравнение х 2 — 2х — 3 = 0. Разложим левую часть на множители: х 2 — 2х — 3 = х 2 +х — 3х — 3 = х(х + 1) — 3(х + 1) = (х + 1)(х — 3).

Следовательно, уравнение можно переписать так: (х + 1)(х — 3) = 0

Так как произведение равно нулю, значит, один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = -1, а также при х = 3. Это означает, что числа -1 и 3 являются корнями уравнения х 2 — 2х — 3 = 0. Данный способ не рассматривается отдельно в учебниках алгебры. Сложность его применения заключается в том, что нужно суметь правильно найти все слагаемые для группировки.

3.4. Решение уравнений способом «переброски»

Рассмотрим квадратное уравнение: ах 2 + bх + с = 0, где а ≠ 0.

Умножая обе его части на а, получаем уравнение: а 2 х 2 + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у 2 + by + ас = 0,

равносильному данному. Его корни у₁ и у₂ найдем с помощью теоремы Виета. Окончательно получаем х₁ = у₁/а и х₁ = у₂/а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски».

Решим уравнение 6х 2 + 7х + 1 = 0.

«Перебросим» коэффициент 6 к свободному члену, в результате получим уравнение: у 2 + 7у +6 = 0. Согласно теореме Виета: у₁ = -6; у₂ = -1, следовательно х₁ = -6/6 = -1 и х₂ = -1/6. [6]

Этот способ описывается в учебнике «Алгебра» для углубленного изучения, автор — А.Г. Мордкович. Его применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

3.5. Решение уравнений по сумме коэффициентов

Возьмем уравнение , где :

— если a + b + c = 0, то , а ,

-если a – b + c = 0, то , а .

Решим уравнение: по сумме коэффициентов.

а + b + c = 11 – 33 + 22 = 33 – 33 = 0, следовательно , а .

Решим уравнение: по сумме коэффициентов.

а – b + c = 5 – 12 + 7 = 12 – 12 = 0, следовательно , а .

Этим способом очень удобно пользоваться, если a,b,c – достаточно большие целые числа. [8]

Решим уравнение: т.к.

Решим уравнение: т.к.

Этот способ не рассматривается ни в одном из учебников алгебры, хотя достаточно прост и не требует больших усилий, однако не каждое квадратное уравнение можно решить этим способом.

3.6. Квадратное уравнение с целыми коэффициентами

Если квадратное уравнение имеет целый корень, то он является делителем свободного члена.

Решим уравнение: 5х 2 -14х-3=0. Сначала нужно выписать все делители свободного члена: 1; -1; 3 и -3. Затем подстановкой проверим, какое из этих чисел является корнем уравнения. Итак, число х₁=3 – корень уравнения. А второй корень можно найти, воспользовавшись соотношением х₁х₂=с/а, то есть 3х₂=-3/5, х₂=-1/5. [4]Этим способом удобно пользоваться, если свободный член не имеет много делителей. Такой прием решения квадратных уравнений мы обнаружили в учебнике, автором которого является Г.В. Дорофеев.

3.7. Закономерность коэффициентов

Все эти свойства коэффициентов позволяют значительно сэкономить время при решении уравнений, но не все уравнения можно решать таким способом, ни в одном учебнике алгебры он не рассматривается.

Таким образом, проанализировав учебники алгебры за 8 класс вышеперечисленных авторов, а также воспользовавшись интернет ресурсами, было выявлено десять различных способов решения квадратных уравнений, из которых семь мы считаем нестандартными.

Мы решили провести социологический опрос среди учащихся 9 классов нашей гимназии, чтобы выяснить, умеют ли ребята решать квадратные уравнения разными способами. В опросе участвовало 53 ученика 9 «А» и 9 «Б» классов.

В качестве основных вопросов были:

Запишите формулу квадратного уравнения.

Сколько способов решения квадратных уравнений вы знаете?

Решите квадратное уравнение: х 2 +х-6=0.

Как вы считаете, умение решать квадратные уравнения поможет в успешной сдаче ОГЭ?

По результатам опроса были получены следующие данные: 56% учащихся верно записали формулу квадратного уравнения, 38% вместо формулы уравнения написали формулы дискриминанта и корней квадратного уравнения и 6% (3 человека) не вспомнили ни одной формулы. На следующий вопрос «Сколько способов решения квадратных уравнений вы знаете?» 10% написали 3 способа, 67% вспомнили два способа (через дискриминант и по теореме Виета), 19% только один способ и 2 человека (4%) не назвали ни одного способа. Дальше ребятам было предложено решить квадратное уравнение, которое является приведенным, что позволило его решить несколькими способами. 60% учащихся верно выполнили задание, из них 10 человек решили уравнение двумя способами, 22% допустили ошибки в решении, а 18% (9 человек) не стали решать. И на последний вопрос « Как вы считаете, умение решать квадратные уравнения поможет в успешной сдаче ОГЭ?» «да» — ответили все девятиклассники. (Приложение 1)

Таким образом, можно сделать вывод, что большинство девятиклассников нашей гимназии успешно справляются с решением квадратных уравнений, но пользуются при этом в основном только одним способом, решают по формулам, так как не знакомы с другими способами, которые позволяют решать квадратные уравнения намного проще и быстрее. Это в очередной раз доказывает актуальность нашей темы.

В ходе настоящего исследования мы проанализировали литературу, чтобы познакомиться с историей возникновения квадратных уравнений, выяснили, что некоторые приемы их решения были известны еще за 2000 лет до нашей эры. Таким образом, квадратные уравнения решались нашими далекими предками в самых разных и отдаленных друг от друга странах. Потребность в уравнениях была велика, так как они применялись в строительстве, в военных делах и в бытовых ситуациях.

Проанализировав учебники алгебры за 8 класс следующих авторов: А.Г. Мордкович, Г.В. Дорофеев, С.М. Никольский, Ю.Н. Макарычев, Ш.А. Алимов, Н.Я. Виленкин, А.Г. Мерзляк, Г.К. Муравин, мы пришли к выводу, что самыми распространенными способами решения квадратных уравнений являются способы решения по формуле, то есть через дискриминант, и по теореме Виета. Такие способы, как выделение квадрата двучлена, решение уравнений с четным коэффициентом при х; рассматриваются также в каждом учебнике алгебры. Разложение левой части уравнения на множители и графический способ решения квадратных уравнений мы встретили только в учебнике А.Г. Мордковича. Автор предлагает пять различных способов решения уравнения при помощи построения разных графиков. Также в учебнике А.Г. Мордковича, но уже для углубленного изучения, мы познакомились со способом «переброски». В учебнике, автором которого является Г.В. Дорофеев, мы познакомились с интересным способом решения уравнений с целыми коэффициентами, этот способ автор поместил в раздел «Для тех, кому интересно». Пользуясь ресурсами интернета, нами были найдены еще два нестандартных способа решения квадратных уравнений: решение уравнений по сумме коэффициентов и с использованием закономерности коэффициентов. Эти способы вызвали большой интерес, так как они позволяют достаточно легко и быстро находить корни, но достаточно сложно все эти свойства запомнить, поэтому мы решили сделать памятку и пользоваться ей по необходимости (приложение 2). Эту же памятку мы раздали девятиклассникам, среди которых проводили опрос, так как результаты показали (приложение 1), что учащиеся в основном решают квадратные уравнения по формуле дискриминанта.

Рассмотренный нами материал могут использовать учителя математики на уроках, при проведении внеурочных занятий, также при подготовке выпускников к сдаче ОГЭ и ЕГЭ.

Нам было очень интересно работать над данной темой. Мы узнали, что автор учебника, который мы изучаем на уроках алгебры, А.Г. Мордкович, учит нас решать квадратные уравнения не только традиционными способами, но и рассматривает четыре нестандартных способа, которые не встречаются больше ни в одном учебнике у других авторов. Так же мы познакомились с нестандартными способами решения квадратных уравнений, которые позволяют быстро и рационально их решать. Овладение этими способами поможет сэкономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов.

В дальнейшем мы планируем продолжить работу над этой темой и рассмотреть более сложные способы решения квадратных уравнений.

Список используемой литературы:

Алгебра. 8 класс: учеб. для общеобразоват. Организаций / [Ю.Н. Макарычев, Н.Г. Миндюк и др]; под ред. Н.А. Теляковского.-М.: Просвещение.-2013.-287с.

Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [С.М.Никольский, К. Потапов, Н.Н. Решетников, А.В. Шевкин].-3-е изд.-М.: Просвещение, АО «Московские учебники», 2006.-287с.

Алгебра. 8 класс: учеб для общеобразоват. организаций / [Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин].- М.: Просвещение, 2013.- 336с.

Алгебра. 8 класс: учеб. для общеобразоват. учреждений / [Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др.]; под ред. Г.В. Дорофеева; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение».-5-е изд.-М.: Просвещение, 2010.-288с.

Мерзляк, А.Г. Алгебра: 8 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.- М.: Вентана-Граф, 2013.-256с.

Мордкович, А.Г. Алгебра. 8 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений/ А.Г. Мордкович.- М.: Мнемозина, 2016-215с.

Муравин, Г.К. Алгебра. 8 кл.: учеб. для общеобразоват. учреждений/ Г.К. Муравин, К.С. Муравин, О.В. Муравина.- 15-е изд.,стереотип.-М.: Дрофа, 2013.-254с.