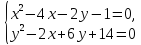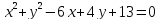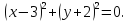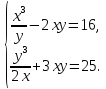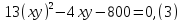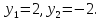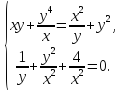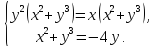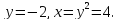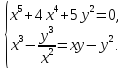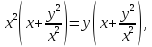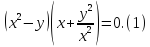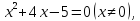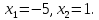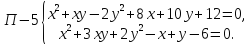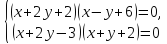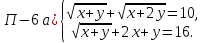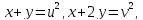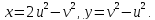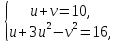Нестандартные уравнения и система уравнений курсовая

Курсовая работа: Нестандартные методы решения уравнений и неравенств

ВВЕДЕНИЕ

1 ИСТОРИЧЕСКАЯ СПРАВКА

2 РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ФУНКЦИИ

2.1 Использование монотонности функции

2.2 Использование ограниченности функции

2.3 Использование периодичности функции

2.4 Использование четности функции

2.5 Использование ОДЗ функции

3 НЕКОТОРЫЕ ИСКУССТВЕННЫЕ СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ

3.1 Умножение уравнения на функцию

3.2 Угадывание корня уравнения

3.3 Использование симметричности уравнения

3.4 Исследование уравнения на промежутках действительной оси

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Не всякое уравнение или неравенство в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению (неравенству) того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях иногда оказывается полезным использовать другие методы решения, речь о которых и пойдет в ходе данной работы. Выше сказанное определяет актуальность курсовой работы. Объект исследования – уравнения и неравенства, не поддающиеся решению с помощью стандартных методов, или отличающиеся громоздкостью стандартного решения.

Целью данной работы является ознакомление с нестандартными методами решения уравнений и неравенств.

Для достижения поставленной цели в данной работе решались следующие задачи:

1.Собрать сведения из истории математики о решении уравнений.

2.Рассмотреть и применить на практике методы решения уравнений и неравенств, основанные на использовании свойств функции.

3.Рассмотреть и применить на практике дополнительные нестандартные методы решения уравнений и неравенств

Практическая значимость работы состоит в том, что не всегда при решении сложных уравнений или неравенств следует идти по «накатанной колее», пытаясь найти решение «в лоб»: достаточно лишь взглянуть на него и найти зацепку, позволяющую избежать сложных вычислений и преобразований. Курсовая работа состоит из введения, трех глав и списка использованных источников. В первой главе приведены некоторые сведения из истории математики о решении уравнений. Во второй главе рассмотрены методы решения, основанные на использовании свойств функции. Третья глава посвящена рассмотрению дополнительных (искусственных) методов решения.

1 ИСТОРИЧЕСКАЯ СПРАВКА

Уравнения и системы уравнений математики умели решать очень давно. В «Арифметике» греческого математика из Александрии Диофанта (III в.) еще не было систематического изложения алгебры, однако в ней содержался ряд задач, решаемых при помощи составления уравнений. Есть в ней такая задача:

«Найти два числа по их сумме 20 и произведению 96». [16]

Чтобы избежать решения квадратного уравнения общего вида, к которому приводит обозначение одного из чисел буквой и которое тогда еще не умели решать, Диофант обозначал неизвестные числа 10 + х и 10-х (в современной записи) и получал неполное квадратное уравнение 100-х 2 = 96, для которого указывал лишь положительный корень 2.

Задачи на квадратные уравнения встречаются в трудах индийских математиков уже с V в. н. э.

Квадратные уравнения классифицируются в трактате «Краткая книга об исчислении алгебры и алмукабалы» Мухаммеда аль-Хорезми (787 — ок. 850). В нем рассмотрены и решены (в геометрической форме) 6 видов квадратных уравнений, содержащих в обеих частях только члены с положительными коэффициентами. При этом рассматривались только положительные корни уравнений.

В работах европейских математиков XIII — XVI вв. даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов в общее правило произвел немецкий математик Михаэль Штифель (1487 — 1567), который рассматривал уже и отрицательные корни.

В самом известном российском учебнике «Арифметика» Леонтия Филипповича Магницкого (1669—1739) имелось немало задач на квадратные уравнения. Вот одна из них:

«Некий генерал хочет с 5000 человек баталию учинить, и чтобы та была в лице вдвое, нежели в стороне. Колико оная баталия будет иметь в лице и в стороне?», т. е. сколько солдат надо поставить по фронту и сколько им в затылок, чтобы число солдат по фронту было в 2 раза больше числа солдат, расположенных им «в затылок»?

В древневавилонских текстах (3000 — 2000 лет до н. э.) встречаются и задачи, решаемые теперь с помощью систем уравнений, содержащих и уравнения второй степени. Приведем одну из них:

«Площади двух своих квадратов я сложил: 25 . Сторона второго квадрата равна стороны первого и еще 5».

Соответствующая система в современной записи имеет вид:

Эту задачу вавилонский автор решает правильно методом, который мы теперь называем методом подстановки, но он еще не пользовался алгебраической символикой.

В XVI в. французский математик Франсуа Виет (1540 — 1603), служивший шифровальщиком при дворе французского короля, впервые ввел буквенные обозначения не только для неизвестных величин, но и для данных, т. е. коэффициентов уравнений. Ф. Виет для обозначения нерасшифрованных букв в донесениях противника использовал редкие буквы латинского алфавита х, у и z, что и положило начало традиции обозначать неизвестные в уравнениях буквами х, у и z. Особенно ценил Виет открытые им формулы, которые теперь называются формулами Виета. Однако сам Виет признавал только положительные корни.

Лишь в ХVII в. после работ Декарта, Ньютона и других математиков решение квадратных уравнений приняло современный вид.

Вернемся в начало XVI в. Тогда профессор математики болонского университета Сципион дель Ферро (1465—1526) впервые нашел алгебраическое решение уравнения третьей степени вида

где р и q – числа положительные.

Это открытие, по обычаям того времени, профессор держал в строгом секрете. О нем знали лишь два его ученика, в том числе некий Фиоре. Утаивание математических открытий тогда было обычным явлением, так как в Италии практиковались математические диспуты-поединки. На многолюдных собраниях противники предлагали друг другу задачи для решения на месте или в определенный срок. Чаще всего это были задачи по алгебре, которую называли тогда великим искусством. Побеждал тот, кто решал больше задач. Победитель не только награждался славой и назначенным денежным призом, но и мог занять университетскую кафедру, а потерпевший поражение часто терял занимаемое место. Вот почему участнику диспута было важно обладать неизвестным другим алгоритмом решения некоторых задач.

После смерти профессора дель Ферро его ученик Фиоре, который сам не был глубоким математиком, вызвал на публичный диспут одного из виднейших математиков того времени Никколо Тарталья (1499—1557). Готовясь к диспуту, Тарталья открыл формулу для нахождения корней кубических уравнений в радикалах, так как предполагал, что Фиоре уже обладал этой формулой. Позднее Тарталья писал: «Я приложил все свое рвение, усердие и уменье, чтобы найти правило для решения кубических уравнений, и, благодаря благословенной судьбе, мне удалось это сделать за 8 дней до срока».

Диспут состоялся 20 февраля 1535 г. Тарталья в течение двух часов решил 30 задач, предложенных ему противником, а Фиоре не смог решить ни одной из 30 задач, предложенных Тартальей. После диспута Тарталья стал знаменитым во всей Италии, но продолжал держать открытую формулу в секрете.

Другой итальянский математик Джерол. но (1501 — 1576) узнал от Тартальи правило решения кубического уравнения (1) и дал «священную клятву», что никому не раскроет этой тайны. Правда, Тарталья лишь частично раскрыл свою тайну, но Кардано, познакомившись с рукописями покойного профессора дель Ферро, получил полную ясность в этом вопросе. В 1545 г. Кардано опубликовал знаменитый свой труд «О великом искусстве, или об алгебраических вещах, в одной книге», где впервые опубликовал формулу для решения уравнения (1), а кубическое уравнение общего вида предлагал свести к уравнению (1).

После выхода в свет этой книги Кардано был обвинен Тартальей в нарушении клятвы, но формула, открытая дель Ферро и Тартальей, и по сей день называется формулой Кардано.

Такова полная драматизма история открытия формулы корней кубического уравнения (1).

В той же книге Кардано привел алгебраическое решение уравнения четвертой степени. Это открытие сделал один из его учеников Лудовико Феррари (1522 — 1565). После этого начались настойчивые поиски формул, которые сводили бы решение уравнений высших степеней к извлечению корней («решение в радикалах»). Эти поиски продолжались около трех столетий, и лишь в начале XIX в. норвежский ученый Нильс Хенрик Абель (1802 —1829) и французский ученый Эварист Галуа (1811 —1832) доказали, что уравнения степеней выше четвертой в общем случае в радикалах не решаются.

Математик и философ Рене Декарт (1596 —1650) впервые сформулировал в своей книге «Геометрия» основную теорему алгебры о числе корней уравнения n-й степени. При этом Декарт допускал существование не только истинных (положительных) и ложных (меньших, чем ничего, т. е. меньших нуля — отрицательных) корней, но и воображаемых, мнимых (у Декарта — imaginaires), т. е. комплексных корней.

Еще в древности математики в процессе решения задач сталкивались с извлечением корня квадратного из отрицательного числа; в этом случае задача считалась неразрешимой. Однако постепенно выяснялось, что решение многих задач, задаваемых в действительных числах, получает простое объяснение при помощи выражений a + bi, где i 2 = -1, которые в конце концов тоже стали называть числами, но уже комплексными. Первое обоснование простейших действий над комплексными числами дал итальянский математик Раффаэле Бомбелли (ок. 1530 —1572) в 1572 г., хотя еще долгое время к комплексным числам относились как к чему-то сверхъестественному.

Академик Петербургской академии наук Леонард Эйлер (1707 —1783) внес существенный вклад в вопросы теории комплексных чисел. После его работ комплексные числа получили окончательное признание как предмет и средство изучения. Само название «комплексное число» было предложено в 1831 г. немецким математиком Карлом Фридрихом Гауссом (1777 — 1855).

В настоящее время комплексные числа широко употребляются во многих вопросах физики и техники.

Выше речь шла об алгебраических уравнениях, т. е. уравнениях f(x) = O, где f(x) — многочлен относительно х.

Кроме алгебраических уравнений, есть еще и трансцендентные уравнения: показательные, логарифмические, тригонометрические и др. Решение трансцендентных уравнений, а также неравенств существенно опирается на свойства функций, которые изучаются в математике относительно недавно.

Особое место среди алгебраических уравнений занимают так называемые диофантовы уравнения, т. е. уравнения, в которых неизвестных больше одной.

Наиболее известными из них являются линейные диофантовы уравнения. Примеры задач, приводящих к линейным диофантовым уравнениям, находим в сборнике задач монаха Алькуина, приглашенного в 795 г. Карлом Великим преподавать в первую из известных школ в г. Аахен. Вот эта задача:

«100 шеффелей (денежных единиц) разделили между мужчинами, женщинами и детьми (число персон 100) и дали при этом мужчинам по 3 шеффеля, женщинам по 2 и детям по шеффеля. Сколько было мужчин, женщин и детей?»

Обозначив количество мужчин за х, количество женщин за у, мы придем к уравнению

Зх + 2y+ (100-х-y)= 100

Общего решения линейных диофантовых уравнений в те времена еще не знали и довольствовались лишь несколькими решениями, удовлетворяющими условию задачи. У самого Алькуина было приведено лишь одно решение этой задачи: мужчин, женщин и детей было 11, 15 и 74, а задача имеет 784 решения в натуральных числах.

Задачи, приводящие к линейным диофантовым уравнениям, имелись у Леонардо Пизанского (Фибоначчи) (1180 — 1240), в «Арифметике» Л. Ф. Магницкого.

Известное диофантово уравнение Пифагора (VI в. до н. э.) х 2 + у 2 = z 2 решают в натуральных числах. Его решениями служат тройки чисел (х; у; z):

x = (m 2 -n 2 )l, y = 2mnl, z = (m 2 + n 2 )l,

где т, п, l — любые натуральные числа (т> п). Эти формулы помогают находить прямоугольные треугольники, длины сторон которых являются натуральными числами.

В 1630 г. французский математик Пьер Ферма (1601 — 1665) сформулировал гипотезу, которую называют великой (или большой) теоремой Ферма: «Уравнение х п + у п = z n для натурального п ≥ 3 не имеет решений в натуральных числах». Ферма не доказал свою теорему в общем случае, но известна его запись на полях «Арифметики» Диофанта: «. невозможно куб записать в виде суммы двух кубов, или четную степень в виде суммы таких же степеней, или вообще любое число, которое является степенью большей, чем вторая, нельзя записать в виде суммы двух таких же степеней. У меня есть поистине удивительное доказательство этого утверждения, но поля эти слишком узки, чтобы его уместить». Позднее в бумагах Ферма было найдено доказательство его теоремы для п= 4. С тех пор более 300 лет математики пытались доказать великую теорему Ферма. В 1770 г. Л.Эйлер доказал теорему Ферма для п = 3, в 1825 г. Адриен Лежандр (1752 1833) и Петер Дирихле (1805 — 1859) — для п = 5. Доказательство великой теоремы Ферма в общем случае не удавалось долгие годы. И только в 1995 г. Эндрю Вайлс доказал эту теорему.

Не всякое уравнение f(x) = g(x) или неравенство в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению или неравенству того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях иногда оказывается полезным использовать некоторые свойства функций, такие как монотонность, периодичность, ограниченность, четность и др.

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ f (x₂ ).

На показанном на рисунке 1 графике

Функция y = f (x), , возрастает на каждом из промежутков [a; x₁ ) и (x₂ ; b] и убывает на промежутке (x₁ ; x₂ ). Обратите внимание, что функция возрастает на каждом из промежутков [a; x₁ ) и (x₂ ; b], но не на объединении промежутков

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ 0) и f + c также возрастают, а функция cf (c n где nN, также возрастает.

· Если функция f возрастает и n – нечетное число, то f также возрастает.

· Композиция g (f (x)) возрастающих функций f и g также возрастает.

Аналогичные утверждения можно сформулировать и для убывающей функции.

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).

Точки, в которых достигается максимум или минимум функции, называются точками экстремума.

В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

Если для любого (x ≠ a) выполняется неравенство f (x) ≤ f (a) , то точка a называется точкой наибольшего значения функции на множестве D:

Если для любого (x ≠ b) выполняется неравенство f (x) > f (b) , то точка b называется точкой наименьшего значения функции на множестве D.

Точка наибольшего или наименьшего значения функции на множестве D может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.

Решение уравнений и неравенств с использованием свойства монотонности основывается на следующих утверждениях.

1. Пусть f(х) — непрерывная и строго монотонная функция на промежутке Т , тогда уравнение f(x) = С, где С — данная константа, может иметь не более одного решения на промежутке Т.

2. Пусть f(x) и g(х) — непрерывные на промежутке T функции, f(x) строго возрастает, а g(х) строго убывает на этом промежутке, тогда уравнение f(х) = =g(х) может иметь не более одного решения на промежутке Т. Отметим, что в качестве промежутка T могут быть бесконечный промежуток (-∞;+∞) , промежутки (а;+∞), (-∞; а), [а;+∞), (-∞; b], отрезки, интервалы и полуинтервалы.

Пример 2.1.1 Решите уравнение

. [28] (1)

Решение. Очевидно, что х ≤ 0 не может являться решением данного уравнения, так как тогда . Для х > 0 функция непрерывна и строго возрастает, как произведение двух непрерывных положительных строго возрастающих для этих х функций f(x) = х и . Значит, в области х > 0 функция принимает каждое свое значение ровно в одной точке. Легко видеть, что х = 1 является решением данного уравнения, следовательно, это его единственное решение.

Пример 2.1.2Решите неравенство

. (2)

Решение. Каждая из функций у = 2 x , у = 3 x , у = 4 х непрерывная и строго возрастающая на всей оси. Значит, такой же является и исходная функция . Легко видеть, что при х = 0 функция принимает значение 3. В силу непрерывности и строгой монотонности этой функции при х > 0 имеем , при х 2 . Примером функции, ограниченной сверху на множестве (–∞; 0) является функция y = 1/x. Примером функции, ограниченной на всей числовой оси, является функция y = sin x.

Пример 2.2.1 Решите уравнение

sin(x 3 + 2х 2 + 1) = х 2 + 2х + 2. (4)

Решение. Для любого действительного числа х имеем sin(x 3 + 2х 2 + 1) ≤ 1, х 2 + 2х + 2 = (x + 1) 2 +1 ≥ 1. Поскольку для любого значения х левая часть уравнения не превосходит единицы, а правая часть всегда не меньше единицы, то данное уравнение может иметь решение только при .

При , , т.е. при уравнение (4) так же корней не имеет .

Пример 2.2.2 Решите уравнение

. (5)

Решение. Очевидно, что х = 0, х = 1, х = -1 являются решениями данного уравнения. Для нахождения других решений в силу нечетности функции f(х) = = x 3 — x — sinπx достаточно найти его решения в области х > 0, х ≠ 1, поскольку если x₀ > 0 является его решением, то и (-x₀ ) также является его решением.

Разобьем множество х > 0, х ≠ 1, на два промежутка: (0; 1) и (1; +∞)

Перепишем начальное уравнение в виде x 3 — x = sinπx. На промежутке (0; 1) функция g(х) = x 3 — x принимает только отрицательные значения, поскольку х 3 3 — х принимает положительные значения, функция h(x) = sinπxпринимает значения разных знаков, причем на промежутке (1; 2] функция h(x) = sinπx неположительна. Следовательно, на промежутке (1; 2] уравнение решений не имеет.

Если же х > 2, то |sinπx| ≤ 1, x 3 — x = x(x 2 — 1) > 2∙3 = 6, а это означает, что и на промежутке (1; +∞) уравнение также не имеет решений.

Итак, x = 0, x = 1 и x = -1 и только они являются решениями исходного уравнения.

Пример 2.2.3 Решите неравенство

. (6)

Решение. ОДЗ неравенства есть все действительные x, кроме x = -1. Разобьем ОДЗ неравенства на три множества: -∞ x > 0. Следовательно, все эти x являются решениями неравенства.

Пусть -1 x ≤ 1. Следовательно, ни одно из этих x не является решением данного неравенства.

Пусть 0 0 и T₂ > 0. Тогда если то функция периодическая с периодом T, равным наименьшему общему кратному чисел T₁ и T_2.

Пример 2.4.1 Функция периодическая с периодом T = 5. Известно, что . Найдите

Решение. Преобразуем отдельно каждое слагаемое:

Тогда

Пример 2.4.2 [24] Найдите период функции

Решение. Преобразуем данное выражение:

имеет период ;

имеет период .

Тогда функция имеет период

Пример 2.4.3 Пусть — периодическая функция с периодом 3 такая, что

; .

(7)

График функции на множестве [0;3) изображен на рисунке 3:

Т.к. 3 — период функции , то , тогда уравнение (7) примет вид , рассмотрим два случая.

1) пусть , т.е. , тогда уравнение примет вид:

, значит и значит,

2) пусть то , тогда уравнение примет вид:

; итак ,

т.е. , .

Ответ: .

Функция f (x) называется четной, если для любого выполняются равенства:

1) ,

График четной функции на всей области определения симметричен относительно оси OY. Примерами четных функций могут служить y = cos x, y = |x|, y = x 2 + |x|

График четной функции

Функция f (x) называется нечетной, если для любого выполняются равенства:

1) ,

Иными словами функция называется нечетной, если ее график на всей области определения симметричен относительно начала координат. Примерами нечетных функций являются y = sin x, y = x 3 .

График нечетной функции

Не следует думать, что любая функция является либо четной, либо нечетной. Так, функция не является ни четной, ни нечетной, так как ее область определения несимметрична относительно начала координат. Область определения функции y = x 3 + 1 охватывает всю числовую ось и поэтому симметрична относительно начала координат, однако f (–1) ≠ f (1). А это значит, что функция не является ни четной, ни нечетной, т. е. является функцией общего вида (ФОВ).

Если область определения функции симметрична относительно начала координат, то эту функцию можно представить в виде суммы четной и нечетной функций.

Таковой суммой является функция

Первое слагаемое является четной функцией, второе – нечетной.

Сравнительная иллюстрация функций разной четности изображена на рисунке 6

Рисунок 6 http://mathematics.ru/courses/function/design/images/buttonModel_h.gif

Исследование функций на четность облегчается следующими утверждениями.

· Сумма четных (нечетных) функций является четной (нечетной) функцией.

· Произведение двух четных или двух нечетных функций является четной функцией.

· Произведение четной и нечетной функции является нечетной функцией.

· Если функция f четна (нечетна), то и функция 1/f четна (нечетна).

Пример 2.4.1 Может ли при каком-нибудь значении а уравнение

2x 8 – 3аx 6 + 4x 4 – аx 2 = 5

Решение. Обозначим f(x) = 2х 8 – 3ах 6 + 4х 4 – ах 2 . f(x) – функция четная, поэтому, если x₀ – корень данного уравнения, то -x₀ – тоже. x = 0 не является корнем данного уравнения (0 ≠ 5). Следовательно, число корней у этого уравнения при любом действительном а четно, поэтому 5 корней оно иметь не может.

Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция определена. Область определения иногда еще называют областью допустимых значений функции (ОДЗ). Для нахождения ОДЗ функции нужно проанализировать данное соответствие и установить встречающиеся запретные операции (деление на нуль, возведение в рациональную степень отрицательного числа, логарифмические операции над отрицательными числами и т. п.).

Иногда знание ОДЗ позволяет доказать, что уравнение (или неравенство) не имеет решений, а иногда позволяет найти решения уравнения (или неравенства) непосредственной подстановкой чисел из ОДЗ.

Пример 2.5.1 Решите уравнение

. (8)

Решение. ОДЗ этого уравнения состоит из всех х, одновременно удовлетворяющих условиям и , т. е. ОДЗ есть пустое множество. Этим решение уравнения и завершается, так как установлено, что ни одно число не может являться решением, т. е. что уравнение не имеет корней.

Пример 2.5.2 Решите уравнение

. (9)

Решение. ОДЗ этого уравнения состоит из всех x, одновременно удовлетворяющих условиям , , , т. е. ОДЗ есть . Подставляя эти значения х в уравнение (9), получаем, что его левая и правая части равны 0, а это означает, что все , являются его решениями.

Ответ:

Пример 2.5.3 Решите неравенство

. (10)

Решение. ОДЗ неравенства (10) есть все х, удовлетворяющие условию . Ясно, что х = 1 не является решением неравенства (10). Для х из промежутка имеем , а . Следовательно, все х из промежутка являются решениями неравенства (10).

Ответ: .

Пример 2.5.4 [26] Решите неравенство

. (11)

Решение. ОДЗ неравенства (11) есть все х из промежутка . Разобьем это множество на два промежутка и .

Для х из промежутка имеем , . Следовательно, на этом промежутке, и поэтому неравенство (11) не имеет решений на этом промежутке.

Пусть х принадлежит промежутку , тогда и . Следовательно, для таких х, и, значит, на этом промежутке неравенство (11) также не имеет решений.

Итак, неравенство (11) решений не имеет.

Существуют и другие нестандартные методы решения уравнений и неравенств, помимо использования свойств функции. Данная глава посвящена дополнительным методам решения.

Иногда решение алгебраического уравнения существенно облегчается, если умножить обе его части на некоторую функцию — многочлен от неизвестной. При этом надо помнить, что возможно появление лишних корней — корней многочлена, на который умножали уравнение. Поэтому надо либо умножать на многочлен, не имеющий корней, и получать равносильное уравнение, либо умножать на многочлен, имеющий корни, и тогда каждый из таких корней надо обязательно подставить в исходное уравнение и установить, является ли это число его корнем.

Пример 3.1.1 Решите уравнение

. (1)

Решение. Умножив обе части уравнения на многочлен , не имеющий корней, получим уравнение

, (2)

равносильное уравнению (1). Уравнение (2) можно записать в виде

. (3)

Ясно, что уравнение (3) не имеет действительных корней, поэтому и уравнение (1) их не имеет.

Пример 3.1.2 [19]Решите уравнение

. (4)

Решение. Умножив обе части этого уравнения на многочлен , получим уравнение

, (5)

являющееся следствием уравнения (4), так как уравнение (5) имеет корень , не являющийся корнем уравнения (4).

Уравнение (5) есть симметрическое уравнение четвертой степени. Поскольку не является корнем уравнения (5), то, разделив обе его части на и перегруппировав его члены, получим уравнение

(6)

равносильное уравнению (5). Обозначив , перепишем равнение (6) в виде

. (7)

Уравнение (7) имеет два корня: и . Поэтому уравнение (6) равносильно совокупности уравнений

и .

Решив каждое из этих уравнений, найдем четыре корня уравнения (6), а тем самым и уравнения (5):

, , ,

Так как корень является посторонним для уравнения (4), то отсюда получаем, что уравнение (4) имеет три корня: x₁ , x₂ , x₃ .

Ответ:

Иногда внешний вид уравнения подсказывает, какое число является корнем уравнения.

Пример 3.2.1 Решите уравнение

. (8)

Решение. Перепишем уравнение (8) в виде:

. (9)

Из внешнего вида этого уравнения очевидно, что х = 12 есть его корень. Для нахождения остальных корней преобразуем многочлен

Так как многочлен не имеет корней, то исходное уравнение имеет единственный корень х = 12.

Пример 3.2.2. Решите уравнение

(10)

Решение. Легко заметить, что и являются решениями этого уравнения. После раскрытия скобок это уравнение перепишется как квадратное. А это означает, что оно может иметь не более двух корней. Так как два корня этого уравнения найдены, то тем самым оно и решено.

Ответ:

Иногда внешний вид уравнения — некоторая его симметричность — подсказывает способ решения уравнения.

Пример 3.3.1Решите уравнение

. (11)

Решение. Очевидно, что внешний вид уравнения подсказывает, что один из корней уравнения (11) есть . Однако найти остальные корни этого уравнения здесь не так просто. Перепишем уравнение (11) в несколько ином виде.

Поскольку справедливы тождественные равенства

,

то уравнение (11) можно переписать так:

. (12)

Теперь очевидно, что если ― корень уравнения (12), то также корень уравнения (12), поскольку

. (13)

Покажем, что если , есть корень уравнения (11), то также есть корень этого уравнения.

Действительно, так как

то отсюда и вытекает это утверждение.

Итак, если , ― корень уравнения (11), то оно имеет еще корни

, , , ,

т. е. уравнение (11) имеет корни

, , , , , .

Поскольку уравнение (11) есть алгебраическое уравнение шестой степени, то оно имеет не более шести корней. Таким образом, мы нашли все корни уравнения (11).

Ответ:

Иногда решения уравнения можно найти, исследуя его на разных числовых промежутках.

Пример 3.4.1 Решите уравнение

. (14)

Решение. Перепишем уравнение в виде или, используя формулу разности

, (15)

. (16)

Отсюда видно, что один из корней данного уравнения есть . Докажем, что уравнение

(17)

решений не имеет.

Разобьем числовую ось на промежутки

Для любого x из промежутка имеем, что левая часть уравнения (17) положительна, поэтому на этом промежутке уравнение решений не имеет.

,

то для любого х из промежутка этот многочлен положителен. Это означает, что на промежутке уравнение (17) также не имеет решений.

,

то для любого x из промежутка этот многочлен положителен. Следовательно, и на промежутке уравнение (17) не имеет решений.

Итак, данное уравнение (17) имеет единственное решение .

В процессе исследования цель курсовой работы достигнута, полностью решены поставленные задачи и получены следующие результаты и выводы:

1.Приведены сведения о давности постановки перед человеком задачи решения уравнений и неравенств.

2.Приведены и рассмотрены на примере методы решения уравнений и неравенств, основанные на использовании свойств функции.

3.Рассмотрены и опробованы дополнительные нестандартные методы решения уравнений и неравенств.

Продолжение исследования может заключаться в изученииприменения свойств синуса и косинуса, применении производной, использовании числовых неравенств, использовании графиков и других нестандартных способов решения уравнений и неравенств.

1. Абылкасымова А. Е. «Алгебра 10 класс», Мектеп, 2006 г.

2. Алилов М. А., Колягин Ю. М. и др. «Алгебра и начала анализа». Пробный учебник для 10-11 кл. средней школы. М.: «Просвещение», 2002 г.

3. Болтянский В. Г., Сидоров Ю. В., Шабунин М. И. «Лекции и задачи по элементарной математике», М.: Изд. «Наука», 1974 г.

4. Газета «Математика» №20, 2008 г.

5. Голубев В. И. «Решение сложных и нестандартных задач по математике», 1995 г.

6. Горштейн П. И. «Задачи с параметрами», М. «Илекса», 1999 г.

7. Гусев В. А., Мордович А. Г. «Математика. Справочные материалы» Книга для учащихся М.: «Просвещение», 1990 г.

8. Далингер В. А. «Нестандартные уравнения и методы их решения», Омск, 1995 г.

9. Жафяров А. Ж. «Профильное обучение старшеклассников», 2001 г.

10. Журнал «Математика в школе», 1999-2007 г.

11. Ивлев Б. М., Абрамов А. М., Дудницын Ю. П., Швардцбурд С. И. «Задачи повышенной трудности по алгебре и началам анализа», М: «Просвещение», 1990 г.

12. Ковалева Г. И., Конкина Е. В. «Функциональный метод решения уравнений и неравенств», 2008 г.

13. Кравцев С. В. «Методы решения задач по алгебре», М. «Оникс», 2001г.

14. Кулагин Е. Д. «300 конкурсных задач по математике», 2003 г.

15. Кушнир А. И. «Математическая энциклопедия», Киев «Астарта», 1995 г.

16. Литвиненко В. Н., Мордкович А. Г. «Практикум по элементарной математике. Алгебра. Тригонометрия», 1991 г.

17. Мордкович А. Г. «Алгебра и начала анализа», М.: Высшая школа, 1995 г.

18. Олехник С. Н., Потапов М. К., Пасиченко П. И. «Нестандартные методы решения», 1992 г.

19. Письменский Д. Т. «Математика для старшеклассников». Издательство, «Айрис». М., 1996 г.

20. Постникова, С. Я. «Уравнения с параметрами на факультативных занятиях», 2002 г.

21. Потапов М. К. «Уравнения и неравенства. Нестандартные методы решения» М. «Дрофа», 2002 г.

22. С. А. Барвенов «Методы решения алгебраических уравнений», М. «Аверсэв», 2006 г.

23. Сканави М. И. «Сборник задач для поступающих в ВУЗы», М. «Высшая школа», 1988г.

24. Супрун В. П. «Нестандартные методы решения задач по математике» Минск «Полымя», 2000 г.

25. Теляковский С. Л. «Алгебра». Учебник для 9 кл. общественных учреждений. М.: «Просвещение», 1995 г.

26. Фридман Л. М., Турецкий Е. Н. «Как научиться решать задачи» Книга для учащихся старших классов средней школы. М.: «Просвещение», 1987 г.

27. Шабунин. М. И. «Пособие по математике для поступающих в вузы», 2005г.

28. Шыныбеков А. Н. «Алгебра 10 класс», Атамура, 2006 г.

Задачи для самостоятельного решения:

1. Докажите, что следующее уравнение не имеет решений:

a. .

b. .

c. .

d. .

e.

2. Решите уравнение:

a.

b. .

c. .

d. .

e. .

f. .

g.

Ответ:.

h. .

Ответ:

3. Решите неравенство:

a. .

Ответ:.

b. .

Ответ:.

c. .

Ответ:.

d. .

Ответ:.

e. .

Ответ:

Читать курсовая по математике: «Нестандартные методы решения уравнений и неравенств» Страница 1

СОДЕРЖАНИЕ ВВЕДЕНИЕ 1 ИСТОРИЧЕСКАЯ СПРАВКА 2 РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ФУНКЦИИ 2.1 Использование монотонности функции 2.2 Использование ограниченности функции 2.3 Использование периодичности функции 2.4 Использование четности функции 2.5 Использование ОДЗ функции 3 НЕКОТОРЫЕ ИСКУССТВЕННЫЕ СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ 3.1 Умножение уравнения на функцию 3.2 Угадывание корня уравнения 3.3 Использование симметричности уравнения 3.4 Исследование уравнения на промежутках действительной оси ЗАКЛЮЧЕНИЕ СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ПРИЛОЖЕНИЕ ВВЕДЕНИЕ Не всякое уравнение или неравенство в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению (неравенству) того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях иногда оказывается полезным использовать другие методы решения, речь о которых и пойдет в ходе данной работы. Выше сказанное определяет актуальность курсовой работы. Объект исследования – уравнения и неравенства, не поддающиеся решению с помощью стандартных методов, или отличающиеся громоздкостью стандартного решения. Целью данной работы является ознакомление с нестандартными методами решения уравнений и неравенств. Для достижения поставленной цели в данной работе решались следующие задачи:

Собрать сведения из истории математики о решении уравнений. Рассмотреть и применить на практике методы решения уравнений и неравенств, основанные на использовании свойств функции. Рассмотреть и применить на практике дополнительные нестандартные методы решения уравнений и неравенств

Практическая значимость работы состоит в том, что не всегда при решении сложных уравнений или неравенств следует идти по «накатанной колее», пытаясь найти решение «в лоб»: достаточно лишь взглянуть на него и найти зацепку, позволяющую избежать сложных вычислений и преобразований. Курсовая работа состоит из введения, трех глав и списка использованных источников. В первой главе приведены некоторые сведения из истории математики о решении уравнений. Во второй главе рассмотрены методы решения, основанные на использовании свойств функции. Третья глава посвящена рассмотрению дополнительных (искусственных) методов решения. 1 ИСТОРИЧЕСКАЯ СПРАВКА Уравнения и системы уравнений математики умели решать очень давно. В «Арифметике» греческого математика из Александрии Диофанта (III в.) еще не было систематического изложения алгебры, однако в ней содержался ряд задач, решаемых при помощи составления уравнений. Есть в ней такая задача: «Найти два числа по их сумме 20 и произведению 96». [16] Чтобы избежать решения квадратного уравнения общего вида, к которому приводит обозначение одного из чисел буквой и которое тогда еще не умели решать, Диофант обозначал неизвестные числа 10 + х и 10-х (в современной записи) и получал неполное квадратное уравнение 100-х2 = 96, для которого указывал лишь положительный корень 2. Задачи на квадратные уравнения встречаются в трудах индийских математиков уже с V в. н. э. Квадратные уравнения классифицируются в трактате «Краткая книга об исчислении алгебры и алмукабалы» Мухаммеда аль-Хорезми (787 —

Нестандартные алгебраические системы уравнений

Мы будем рассматривать только системы уравнений, в которых число уравнений совпадает с числом неизвестных, ибо в плане эффективного, технологичного нахождения множества решений перспективно рассмотрение только таких систем.

Просмотр содержимого документа
«Нестандартные алгебраические системы уравнений»

Тема: «Нестандартные алгебраические системы уравнений»

Решение нестандартных алгебраических систем уравнений. (Основные понятия и методы решений).

1. Основные понятия

2. Различные преобразования и методы решений

3. Решение нестандартных алгебраических систем уравнений известными способами и методом — три «З».

Решение нестандартных алгебраических систем уравнений.

Цель: научиться решать системы уравнений разными способами и известными методами.

Проблема данного исследования: как применять методы при решении систем алгебраических уравнений.

Объектом исследования будут служить нестандартные алгебраические системы уравнений

Предметом – применение методов и различных способов решения алгебраических систем уравнений.

1. Рассмотреть основные понятия систем с двумя и тремя неизвестными (переменными), преобразования и методы решений.

2. Научиться применять различные методы и известные способы при решении нестандартных алгебраических систем уравнений.

3. Обосновать применение метода: Три — «З» при решении нестандартных алгебраических уравнений.

4. Создать компьютерную программу для решения примеров вида П-1и П-11.

Единых способов решения систем нестандартных алгебраических уравнений нет, этот раздел в алгебре считается по праву трудным, поэтому исследуемая тема сегодня особенно актуальна и востребована, особенно при сдаче ЕГЭ, на олимпиадах и конкурсах.

На вступительных экзаменах (где они ещё проводятся) в вузах предлагаются задачи, в которых требуется решить системы алгебраических уравнений или неравенств. Этот раздел алгебры по праву считается одним из трудных, так как нет единых способов решения нетрадиционных систем алгебраических уравнений.

Многие учащиеся вопрос о нахождении решений системы уравнений понимают как формальное выполнение ряда алгебраических преобразований и не обосновывают законность выполняемых преобразований, которые могут привести как к появлению посторонних решений, так и к потере решений. В работе рассмотрим основные понятия и виды различных преобразований систем уравнений с двумя и тремя неизвестными. Решим несколько уравнений своим методом три — «З» (задать, заметить, заключить) и несколько нетрадиционных систем уравнений известными способами, которые ещё надо заметить методом пристального взгляда и применить их.

Мы будем рассматривать только системы уравнений, в которых число уравнений совпадает с числом неизвестных, ибо в плане эффективного, технологичного нахождения множества решений перспективно рассмотрение только таких систем.

Решение нестандартных алгебраических систем уравнений.

1. Основные понятия.

Будем рассматривать системы с двумя и тремя неизвестными (переменными). Систему двух уравнений с двумя неизвестными x и y можно записать в виде

(1)

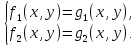
Если левые и правые части уравнений системы (1) являются многочленами от x и y или представляются в виде отношения многочленов, то систему (1) называют алгебраической.

Решением системы (1) называется пара чисел x, y, при подстановке которых соответственно вместо x и y каждое уравнение системы (1) становится верным числовым равенством. Множество решений системы может быть, в частности, пустым. В этом случае говорят, что система не имеет решений (несовместна).

Процесс решения системы обычно состоит в последовательном переходе с помощью некоторых преобразований от данной системы уравнений к другим, более простым, которые мы умеем решать. При этом нужно внимательно следить за тем, чтобы не потерять решения. Что касается посторонних решений для данной системы, то их обычно отсеивают с помощью проверки.

Если в результате преобразований системы (1) получена система:

(2)

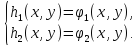
такая, что каждое решение системы (1) является решением системы (2), то система (2) называется следствием системы (1).

называют следствием системы (1), если равенство

является верным для каждой пары чисел x, y, образующих решение системы (1).

Если система (2) является следствием исходной системы (1), а система (1) также является следствием системы (2), то эти системы называют равносильными. Иначе говоря, системы называют равносильными, если множества их решений совпадают. В частности, две системы, не имеющие решений, являются равносильными.

Используя определения равносильности и следствия, можно утверждать, что:

1) если в системе уравнений заменить какое-либо уравнение равносильным, а остальные уравнения оставить без изменения, то полученная при этом система будет равносильна исходной;

2) если к данной системе присоединить уравнение, являющее следствием этой системы, то полученная система будет равносильна исходной;

3) если какое-либо уравнение данной системы заменить его следствием, а остальные уравнения оставить без изменения, то полученная система будет следствием исходной.

Общие средства перехода к равносильной системе немногочисленны. Отметим, во-первых, что простейшие преобразования любого из уравнений системы, такие как перенос, из одной части в другую, вынесение общего множителя за скобки, раскрытие скобок и т. п., не влияют на множество решений, так что приводят к равносильным системам.

Далее, чтобы перейти к равносильной системе, можно выполнить одно из следующих действий:

умножить какие-то из уравнений системы на числа (коэффициенты) и на место одного из затронутых уравнений поставить полученную сумму с коэффициентами;

в одном из уравнений выразить одну неизвестную через остальные и подставить полученное выражение во все оставшиеся уравнения, оставив, разумеется, в системе и данное уравнение;

заменить какое-либо уравнение равносильным ему соотношением (уравнением, системой или совокупностью).

2. Преобразования и методы

При решении систем уравнений нередко приходится применять такие преобразования систем:

как умножение обеих частей уравнения на одно и то же число (или одну и ту же функцию),

почленное сложение, вычитание, умножение и деление уравнений системы, возведение обеих частей уравнения в n-ю степень,

а также часто применяется метод подстановки (метод исключения неизвестного),

с помощью которого решение системы с двумя неизвестными сводится к решению уравнения с одним неизвестным.

Одним из распространённых способов решения систем является замена переменных. Допустим, что в системе удалось выделить какие-то повторяющиеся выражения, составленные из переменных. Тогда если каждое из них обозначить одной новой буквой (разумеется, разные выражения разными буквами), иначе говоря, сделать замену переменных, то наша система превращается в некоторую другую систему относительно новых неизвестных. Если её удаётся решить, то после этого для нахождения корней исходной системы предстоит решить одну или несколько систем, связывающих новые неизвестные со старыми.

3. Метод — три «З» (задать, заметить, заключить). Алгебраические системы:

Найдите действительные решения системы уравнений (1-10).

Мы придумали особый метод для решения алгебраических систем уравнений:

Метод — три «З» (задать, заметить, заключить).

Замечание: применить способ сложения -2 -ое «З»

Заключение: решить, проверить, ответить-3-ье «3»

Решение. Сложив уравнения системы, получим

Пара чисел x = 3 и y = −2, как показывает проверка, образует решение системы.

П –2

Замечание -2-ое –«З»: применить почленное умножение

Заключение -3ье-«З»: решение, (если треб. проверить), ответ

Решение. Запишем систему в виде

Перемножив почленно уравнения этой системы, получим уравнение

которое вместе с одним из уравнений системы (1)−(2) образует систему, равносильную системе (1)−(2).

Из уравнения (3) находим

то есть

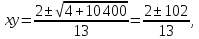
xy = 8 или xy = .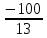

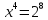
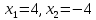
Если xy = 8, то из уравнения (1) следует, что , откуда и тогда

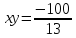
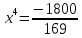
Если , то . Это уравнение не имеет действительных корней.

Замечание -2ое-«З»: xy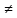0

Задание -1-3 (первое –«З»)

Заключение -3-ье-«З»: решение, (если треб. проверить), ответ

Решение. Так как 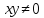, то систему можно записать в виде

Если 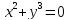, то из второго уравнения следует, что y = 0, что невозможно.

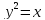
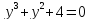
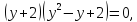
Если , то из второго уравнения системы следует, что или откуда y = −2 (уравнение не имеет действительных корней). Итак,

Задание -1-3 (первое –«З»)

П-4

Замечание -2-ое-«З»: Разложить на множители

Заключение -3-ье –«З»: решение, (если треб. проверить), ответ

Решение. Второе уравнение исходной системы равносильно каждому из уравнений

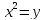
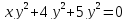
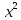
а) Если , то из первого уравнения исходной системы получаем , откуда следует, что либо y = 0, либо x = −9. Но если y = 0, то x = 0, а при x = 0 уравнение (1) теряет смысл. Итак, x = −9, y = = 81.

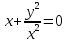
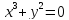
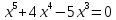
б) Если , то . Из первого уравнения системы находим

или

откуда

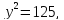
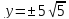
Пусть x = −5, тогда откуда .

Пусть x = 1, тогда 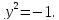Это уравнение не имеет действительных корней.

Таким образом, система имеет три действительных решения: (−9; 81), , .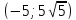

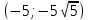
Ответ: (−9; 81), , .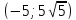

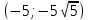
Указание. Решить каждое из уравнений системы как квадратное относительно x или y. Тогда исходная система преобразуется к виду

и равносильна совокупности четырех систем линейных уравнений.

Решение. Пусть , тогда

откуда:

Поэтому исходная система примет вид

Так как u ≥ 0, то u = 4, то есть

П-6 б) Решить уравнение:

Возведём обе части уравнения в третью степень:

Получим: 14-3 • • ( — = х 3

Разложим на множители левую часть уравнения.

Делители свободного члена (-14):

Методом подбора найдём корень: х=2

Разделим х 3 +3х – 14 на х-2, получим (х-2) • (х 2 +2х +7) =0

х 2 +2х +7=0 – не имеет корней, Д 0

х=2, 8+6-14=0, 14=14 –верно. Ответ: х=2

Решение. Область определения уравнения – множество точек таких, что

Преобразуем первое уравнение системы так:

Из (2) и второго уравнения системы получаем или

откуда , так как Тогда Отсюда и из (2) находим

Пара чисел удовлетворяет условиям (1).

, а из второго уравнения находим Поэтому

Пара чисел (12; −2) – решение исходной системы.

8. Решить систему уравнений с тремя неизвестными.

Решение. (Заменой переменных).

Обозначим и запишем исходную систему в следующем виде (1)

Сложив уравнения системы (1) и обозначив получим уравнение , откуда

Подставляя найденные значения суммы в систему (1), найдем искомые значения

9. Решить систему уравнений с тремя неизвестными.

Решение. Складывая уравнения попарно, получим систему

равносильную исходной системе. Перемножим уравнения этой системы и обозначим тогда , или

Решение. Вычитая из первого уравнения второе, получим

Разложим на множители левую часть уравнения:

Заметим, что исходная система равносильная системе, состоящей из ее первого и третьего уравнений и уравнения (1), равносильная также совокупности трех систем, получаемых присоединением к первому и третьему уравнениям соответственно уравнений: (2) (3) (4)

1) Подставляя из уравнения (2) в первое и третье уравнения исходной системы, получаем

Если или то из (5) следует, что 0 = 3.

Если , то из (5) находим

В этом случае система имеет два решения

2) Подставляя (см. (3)) в первое и третье уравнения исходной системы, получаем

Если то из уравнения (6) следует, что 0 = 3.

Если то из уравнения(6) находим

В этом случае система имеет решения

3) Подставляя (см. (4)) в первое и третье уравнения исходной системы, получаем:

Если то из уравнения (7) следует, что 0 = 3.

Если то из уравнения(7) находим

В этом случае система имеет два решения

Системы, содержащие логарифмы

которые удовлетворяют неравенству

Решение. Потенцируя, получаем систему

которая является следствием исходной системы.

а) Пусть и, с учетом условия из первого уравнения системы (1) получаем

Тогда второе уравнение этой системы преобразуется к виду откуда

Здесь для не выполняется условие а для пары не выполняется условие

б) Пусть тогда из системы (1), с учетом условия , получаем , а из второго уравнения следует, что откуда

11 б). Решите систему уравнений:

Решение. Первое уравнение системы можно записать в виде

а множество допустимых значений определяется условием (1)

При выполнении условия (1) исходная система равносильна системе

а система (1)−(2) равносильна совокупности двух систем

Исключая из системы (3), получаем уравнение не имеющее действительных корней. Поэтому система (3) не имеет действительных решений.

Из системы (4) получаем уравнение имеющее корни

Поэтому исходная система имеет два решения:

1. Рассмотрели основные понятия алгебраических систем уравнений, различные методы и способы их решения.

2. Выяснили, в чем состоит процесс решения систем уравнений, определили общие средства перехода к равносильной системе.

3. При решении алгебраических систем уравнений применили как распространенные преобразования и способы, так и другие методы, связывающие новые с традиционными.

Наша школьная математика – это огромный потенциал для использования различных методов и способов для решения нестандартных систем алгебраических уравнений с несколькими переменными, как на уроках, так и на олимпиадах, конкурсах и ЕГЭ.

1. Варианты вступительных экзаменов МФТИ. 1996-2002 г.

2. Учебник-С. М. Никольский, .. 9-10 Кл., 2005-2010 г.

3. В. Н. Дятлов. Этюд №3 Уравнения и системы уравнений. 2013 г.