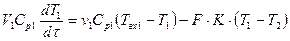Нестационарное температурное поле шара описывается уравнением

Температурное поле стремится к равновесию. Шар

Радиусные шары излучают тепло в окружающую среду через всю внешнюю поверхность. Коэффициент теплопередачи равен A. температура окружающей среды 0 считается нулевой. Начиная с 0, шар везде имеет одинаковую температуру 0°. Кроме того, предположим, что физические константы X, c и p, а следовательно, и a, равны constants. As в зависимости от времени, необходимо определить тип температурного поля и величину теплопотерь. а) математическая постановка задачи. Поскольку температура зависит только от r, используя сферическую систему координат. Дифференциальное уравнение. Первоначальное условие-о * = о = 0С по 0 г И. Р) определение температурного поля.

Заменять это приводит к известному уравнению φ ® (IIc).Решение этого уравнения также известно： Первое решение-это странная функция, поэтому она не подходит для этой задачи. Поэтому остается только решение формы величина n определяется по состоянию поверхности Первые 4 маршрута этого трансцендентального уравнения сведены в таблицу. 4. В общем решении определите только коэффициент Ok. Это можно сделать, используя начальные условия Таблица 4 Корень уравнения Используя слегка измененную формулу (15а), вы получаете: вводя обозначение st, вы достигнете следующей точки в температурном поле.

Проволока нагревается электрически, труба охлаждается снаружи, и измеряются тепловой поток, температуры проволоки и трубы. Людмила Фирмаль

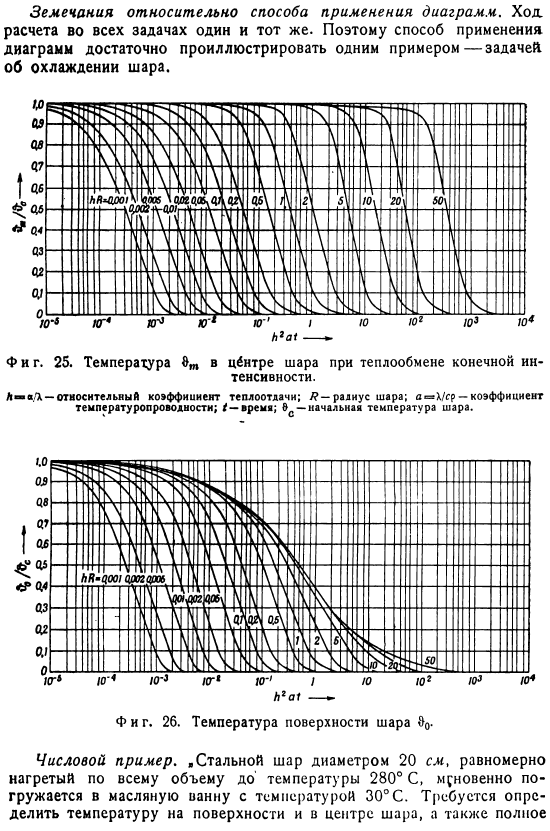
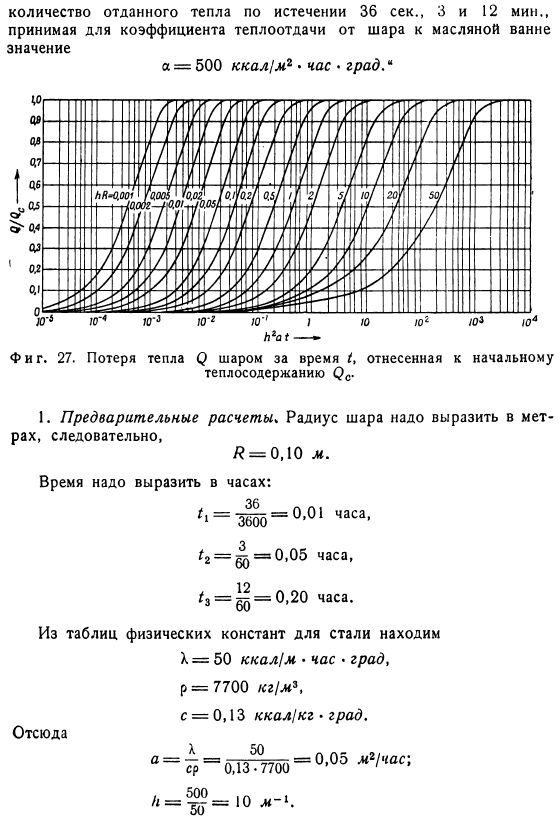
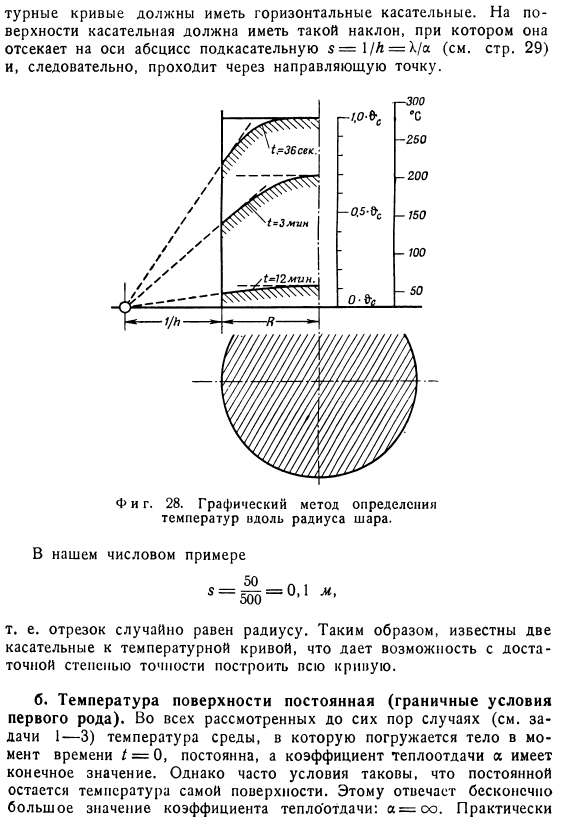
В частном случае AE = oo, 81pool =0.И так оно и есть.、 Чтобы определить температуру центра шара, необходимо принять r = 0 в Формуле (31a).В дальнейшем、 Температура поверхности, R = /?Вы можете получить его, установив его. Подобный этому Т) определение тепловых потерь с>.Формула cp (&c -&) (IV) Класть С интеграцией всего шарика、 Или ^ = Ци^) — 34б> Температура центра шара ($ w) и температура его поверхности (&0) показаны в виде кривой на рисунке 2.Согласно расчетам Бахмана с использованием переменных L /-25 и 26 и H. 2a1.Теплопотери (2) показаны на рисунке 27. Полукруг по способу нанесения рисунка.

Движение. Расчет во всех задачах один и тот же. Поэтому достаточно объяснить, как применить рисунок в Примере 1, то есть проблему охлаждения шара. К2 а!—- *- Тоже фигура. 25.Температура шара при теплопередаче конечной интенсивности # T8 центр. La / X-относительный коэффициент теплопередачи; P-радиус шара. И » X / sr-коэффициент температуропроводности; / time; / C〜начальная температура шара. Пример числового значения. «Стальные шарики диаметром 20 см равномерно нагреваются по всему объему до температуры 280 ° С и мгновенно погружаются в масляную ванну с температурой 30 ° C. It необходимо измерить температуру поверхности и температуру центра шара, а также общую температуру.

Возьмем значение коэффициента теплопередачи от шара к масляной ванне, количество тепла, переданного через 36 секунд, через 3 минуты и через 12 минут а= 500 ккал] м2 * время * город* Тоже фигура. 27.Потери тепла C) шаром в течение времени/, см. начальное количество тепла^ s. 1.Предварительный расчет*поскольку радиус шара должен быть выражен в метрах、 I = 0,10 м Время должно быть выражено в часах. Из таблицы физических констант стали Отсюда 0,05 м2 / час; 2.Вычисление критерия по найденным значениям. Затем вычислите значение fs ？0 = 4•1 ^ 3 •13•7700•280-30）= 1047 ккал. 3.Окончательный результат.

Из диаграммы видно соответствующее опорное отношение 0o / 0v, 0t / 0s и 0!Найдите ОС (&&=280°С-30°С= 250°С) и вычислите температуру О ’ в соответствии с уравнением & ’= 30ч-250 ^ — в°C Для удобства полученные значения суммируются в таблице. Температура поверхности, ° С217. 5 135 45.0 Центральная температура, ° С278 202.5 60.0 Количество отданного тепла, ккал 126 492 963 4.Изменения температуры вдоль radius. In в большинстве случаев при решении технических задач с охлаждением достаточно выяснить температуру поверхности и Центра.

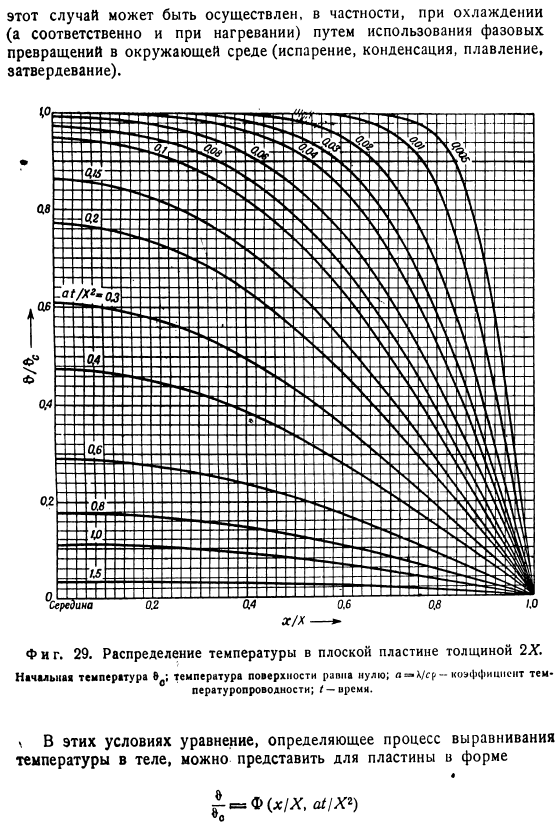
Однако, если вам нужно выяснить все распределение температуры, лучше всего использовать следующие графические методы: (Этот метод также объясняется на примере шара, но он может быть применен таким же образом для цилиндров и пластин.） Поставим его на край радиуса отрезка шара, соответствующего значениям & 0 / 0o и 0t / & 0(рис. 28).Температурная кривая должна проходить через вершины этих вертикалей coordinates. In центр, благодаря симметрии, температурной кривой должен иметь горизонтальную касательную линию. На поверхности касательная должна иметь такой наклон, чтобы она пересекала касательную 5 = 1 /Л=Х/а по оси абсцисс (см. стр. 29) и проходила через направляющую точку. Тоже фигура.

Графический способ определения температуры по радиусу шара. В числовом примере $ = ^ = 0> 1 Это означает, что сегмент случайным образом равен радиусу. Таким образом, известны 2 тангенса к температурной кривой, и вся кривая может быть создана с достаточной точностью. b. температура поверхности постоянна(граничное условие типа 1). во всех рассмотренных до сих пор случаях(см. задачу 1-3) температура среды, в которую погружен объект во времени I = 0,постоянна, а коэффициент теплопередачи a имеет конечное значение. Однако во многих случаях температура самой поверхности остается постоянной. Это соответствует бесконечно большим значениям коэффициента теплоотдачи: а = oo.

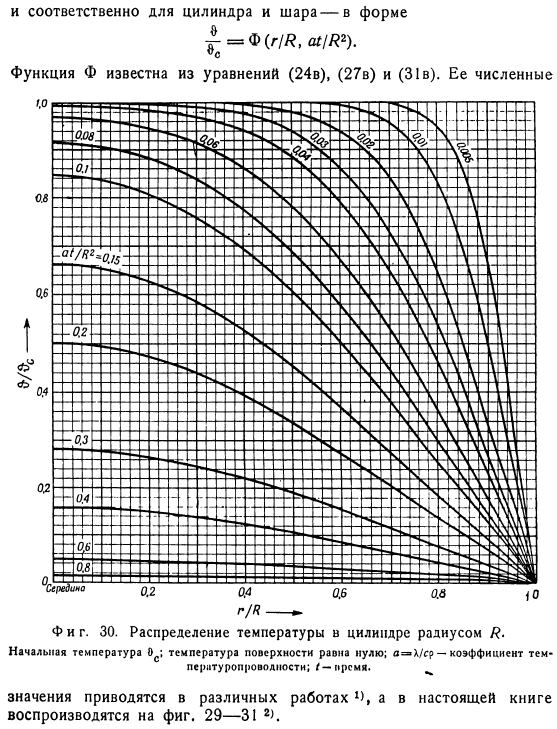
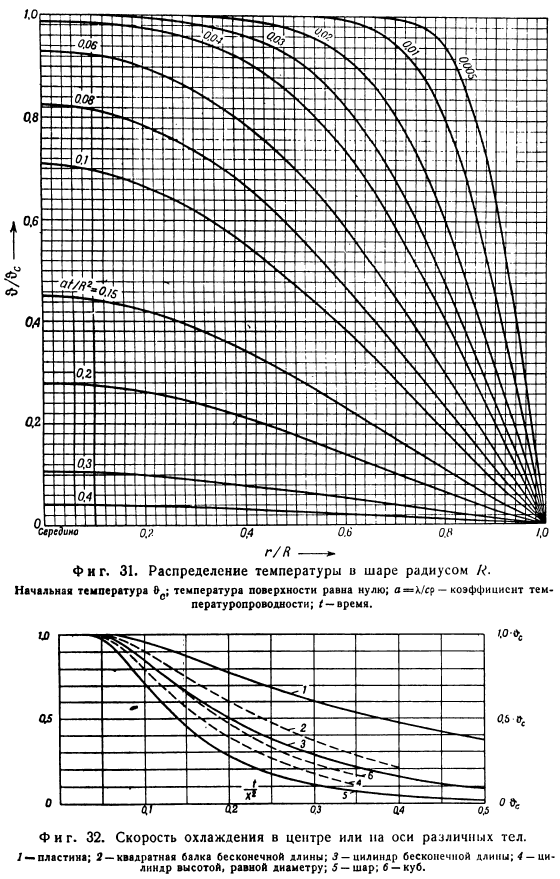
На практике этот случай может быть реализован при охлаждении (а следовательно, и при нагревании) с использованием фазовых переходов (испарение, конденсация, плавление, затвердевание), особенно в окружающей среде. Тоже фигура. 29.Распределение температуры плиты с толщиной 2X. Начальная температура Eo; температура поверхности равна нулю. a-X / sr-коэффициент теплопроводности; / — время. \В этих условиях уравнение, определяющее процесс выравнивания температуры в теле, может быть выражено для пластин вида: F(х / х, / Х2） А для цилиндра и шара соответственно-в виде г //?—— Тоже фигура. 30.Радиус/?Распределение температуры в цилиндре.

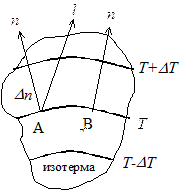
Начальная температура/температура поверхности равна нулю. Коэффициент теплопроводности; I-время. Значения приведены в различных частях 1>и воспроизведены на рисунке 1 в этой книге. 29-31 2. Тоже фигура. 31.Радиус/?Распределение температуры шара. Начальная температура/температура поверхности равна нулю. a = k / sr-коэффициент теплопроводности; / — время. Тоже фигура. 32.Скорость охлаждения по центру или оси различных объектов. / — □Упругая; 2-квадратная балка бесконечной длины. 3-цилиндр бесконечной длины; 4-цилиндр равной высоты с диаметром; 5-шар. Ъ-кубик На рисунке 2 показаны температурные кривые для осевого и среднего времени.

Соотношение площади поверхности и объема увеличивается, скорость охлаждения увеличивается. Таким образом, шар остынет быстрее всего, а тарелка остынет медленнее всего. Сравнение двух кривых на фиг. Критерии 1>18-27 с тем же числовым значением. c. размещение пространственной температуры field. At 6-й во втором рассматривался только в том случае, если тепловой поток направлен в 1 определенное направление.

Теплопроводность газов часто измеряется методом Сутерлен-да, где платиновая проволока встроена вдоль оси капиллярной трубки, заполненной газом, который надо исследовать. Людмила Фирмаль

Однако полученное решение также может быть распространено на 2-D и 3-D нестационарные тепловые потоки, например, цилиндр конечной длины или parallelepiped. In в дальнейшем возможность такого обобщения доказывается на примере двумерного поля с постоянной температурой поверхности. Рассмотрим прямоугольный стержень с удлиненной стороной 2X и 27 в направлении 2 так, чтобы эффект конечного эффекта можно было игнорировать. Пусть стержни везде имеют одинаковую начальную температуру$ s. In кроме того, он начинается с момента 2 = 0 и поддерживает на своей поверхности температуру, которая считается нулевой.

Затем, в процессе выравнивания температуры, дифференциальное уравнение Граница условная если x = + X и y — ^ 7, 0 = 0 И начальные условия Если 2 = 0, ТО 0 = 0. Для 1-мерного поля, то есть для бесконечной пластины толщиной 2X или 27, решение равно 0x / 0s = 1) читатель может неправильно понять, что относительная поверхность шара является самой большой, а относительная поверхность пластины-самой маленькой. Конечно, это не совсем так. Напротив, в действительности, как известно, шар имеет наименьшую относительную поверхность. Если вы сравните кривые охлаждения (или нагрева) объекта на одной и той же поверхности, то сразу увидите, что скорость изменения температуры шара самая низкая.

Соображения, описанные в тексте, относятся к случаю совпадающего тела, основанного на равенстве размеров decisions. In такое сравнение (например, изменение температуры сравнивается в центре шара с радиусом? А на оси бесконечно длинного круглого цилиндра того же радиуса или толщины 2?На центральной плоскости пластины), тело фактически расположено в том порядке, который соответствует рисунку ２. 32.- Приблизительно. = Φ(χ/о, σ//)) или/ /и C =Φ(г / г, А1 / У2).Эти решения показаны на рисунке ４. 29.Пожалуйста, подтвердите Является решением дифференциального уравнения(35).

Для этого используют частные производные предыдущего выражения. Подставляя дифференциальное уравнение(35)、 (35А） По предположению, он удовлетворяет соответствующему 1D Фурье equation. So, уравнение (35a) является тождеством, и поэтому рассматриваемое произведение является правильным решением. Граничные условия также выполняются. Это происходит потому, что на поверхности 1 из 2 факторов всегда равен нулю. Соответственно, показана возможность рассмотрения трехмерного случая (прямоугольный параллелепипед, цилиндр конечной длины).

Если одна из граничных граней отделена, то расстояние от этой границы принимается равным половине толщины (например, X), поэтому полное значение этого расстояния подставляется в критерий. Этот метод не применим к граничным условиям. Однако он эффективен в условиях конечной интенсивности теплопередачи и в случае неограниченного тела с одной стороны (например, конец очень длинного стержня в прямоугольном или цилиндрическом сечении, конец стенки и т.).

На основе этого метода Бергер 1 > рассчитал температурное поле кубоида при теплообмене конечной интенсивности, Ньюман 2)определил температуру поверхности и Центра различных объектов, Олсон и Шульц3) далее предоставил очень точную таблицу средней температуры, плоскости цилиндра при a = oo и стенки конечной толщины.1 согласно Уильямсону и Адамсу, построены 32 такие кривые. Baer 4>дал приближенный метод, в котором используется только первый член ряда, полученный точным решением. Пример числового значения. Диаметр 2 /?Цилиндрический контейнер= 10 см (i = 0,05 м) и высотой 2X = 16 * si (X = 0,08 м), погружают в кипящую воду при температуре 100°С для стерилизации содержимого.

Начальная температура составляет 20°C. влияние стены незначительно. Контейнер заполняется влажной пастой, для которой a = 6.0-10-4 м2 / час берется. Через 1 час (I = 1 час) необходимо определить температуру самой холодной точки (середины) с комплексным подводом тепла (включая дно и крышку). Рассчитать обоим критериям — =6.0 10-4. 1 = 0,094 и-= −6.0：10-4.1 = 0.24。 Х2 64-10″ * /?2 25-10″ * Эти значения аргументов получены из рисунка 1. 29 (для пластин и из рисунка 30 (для цилиндров), безразмерная разница температур в точке x / X = 0, соответственно r //?= 0： — L = 0,96 и-L = 0,4. > с Отсюда мы видим y = 0.96 0.4 = 0.384. Дело в том, что = 100°С-20 ° С= 80°makes составляет= 31,7°С.

Наконец, мы находим 100-31. 7 = 68,3°C для желаемой температуры. Этот численный пример, как показано на фиг. ２. 32 указывает, что эффект торцевой поверхности будет заметен только тогда, когда As установлен ниже(стр. 450).Закон теплопроводности также эффективен для диффузии.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Температурное поле

Температурным полем называется совокупность значений температур в данный момент времени во всех точках рассматриваемого пространства, занятого теплом.

Если температура поля с течением времени t изменяется, то оно называетсянестационарным и описывается уравнением:

где x,y,z – координаты точки поля.

Если же температура в каждой точке поля с течением времени t, остается неизменной, то такое температурное поле называетсястационарным. Температура, в этом случае, является функцией только пространственных координат

В каждый момент времени в температурном поле можно выделить поверхности, имеющие одинаковые температуры. Такие поверхности называются изотермическими. В стационарном температурном поле изотермические поверхности с течением времени не меняют свой вид и расположение, в то время как в нестационарном поле они со временем изменяются.

Одной из характеристик температурного поля является температурный градиент, представляющий собой вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры. На рис.4.1. изображены изотермические поверхности, температуры которых отличаются на DТ.

Рис. 1. К понятию температурного градиента

Из рисунка видно, что интенсивность изменения температуры по разным направлениям (из точки А лучи п и l) неодинакова. Наибольшая разность температур на единицу длины наблюдается в направление нормали п к изотермической поверхности в точке А, так как расстояние между соседними изотермами Dn при этом меньше, чем в точке В.

Предел отношения изменения температуры DТ к расстоянию между изотермами по нормали Dn, когда Dn стремится к нулю, называетсятемпературным градиентом:

В общем случае для различных точек одной и той же изотермической поверхности (например, для точек А и В) градиент температуры различен не только по направлению, но и по величине. За положительное направление градиента принято направление возрастания температур.

Основы теплового расчета

Несмотря на многообразие конструкций и принципов работы теплообменных аппаратов, процессы теплообмена в них подчиняются общим закономерностям, а основные положения методики их расчета могут быть рассмотрены в общей постановке.

До недавнего времени расчет теплообменных аппаратов приводился только для стационарных режимов, и при этом в основном решались две задачи:

1. Для заданных параметров на входе и выходе из аппарата и типе теплообменной поверхности определить требуемую площадь поверхности теплообмена и произвести его конструктивную разработку. Это есть проектный расчет.

2. Для реально существующего аппарата при заданных параметрах потоков на входе определить количество передаваемой теплоты и параметры потоков на выходе из аппарата. Это задача проверочного расчета.

К этим двум задачам можно добавить третью, так называемый оптимальный расчет теплообменного аппарата. Решение этой задачи возможно благодаря использованию ЭВМ. Суть этой задачи сводится к расчету оптимального теплообменника по выбранному критерию.

Тепловой расчет теплообменных аппаратов базируется на уравнениях теплового баланса и теплопередачи.

Решение нестационарных задач теплообмена возможно только при использовании математических моделей, записанных на основе моделей структуры потоков теплоносителей.

Проектный расчет теплообменного аппарата

Задачей проектного расчета является определение геометрических размеров и режима работы теплообменника, необходимого для отвода или подвода заданного количества теплоты к теплоносителю.

При проектном расчете задают:

1. Тип аппарата и общие геометрические характеристики поверхности теплообмена (размеры труб, оребрения, толщина стенок и др.).

2. Параметры теплоносителей на входе и выходе из аппарата (температура, давление и т.д.)

3. Тепловую мощность аппарата Q или расход сред.

Взаимность изменений температур теплоносителей определяется условием теплового баланса, которое для бесконечно малого элемента теплообменника имеет вид:

Здесь G₁, G₂, C_p₁, C_P₂ – расходы и теплоемкости теплоносителей 1 и 2, T₁ и Т₂ – их температуры в произвольном сечении аппарата. Уравнение теплового баланса для всего аппарата получается путем интегрирования уравнения (4.4) и имеет вид:

Уравнение (4.5) содержит две неизвестные: G₁ или G₂ и T_k₁ или T_k₂. Следовательно, это уравнение является неопределенным. Общий прием решения этих задач заключается в использовании метода последовательных приближений, состоящего в том, что в начале принимаются определенные решения относительно конструкции аппарата и неизвестных технологических параметров, затем путем пересчета проверяется до получения результатов с желаемой степенью точности.

Проверочный расчет теплообменного аппарата

Целью проверочного расчета теплообменного аппарата заданной конструкции является определение его мощности и температур потоков на выходе Т_k1, T_k₂ при заданных площадях поверхности теплообмена F, расхода сред G₁, G₂ и их температурах на входе Т_h1 и Т_h2.

Математические модели теплообменников

Обычно принимают, что движение потоков теплоносителя и хладоагента характеризуется гидродинамическими моделями идеального смешения, идеального вытеснения, ячеечной моделью ОДМ или их комбинацией.

Если гидродинамическая структура потоков в теплообменном аппарате соответствует модели идеального смешения, то во всем потоке происходит полное смешение молекул потока. В таком случае любое изменение температуры потока на входе в зону идеального смешения мгновенно распространяется по всему объему зоны.

Гидродинамическая структура потоков теплоносителя, соответствующая модели идеального смешения, имеет место в теплообменных аппаратах с изменением агрегатного состояния потоков – в конденсаторах, кипятильниках, испарителях. Уравнение, описывающее изменение температуры для теплообменника в зоне идеального смешения, имеет вид:

, (6)

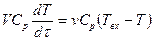
где V – объем зоны идеального смешения; v – объемная скорость; Т_вх, Т – температура потока на входе и в зоне идеального смешения; С_р – теплоемкость потока; t – время.

Условие физической реализуемости модели идеального вытеснения выполняются в случае поршневого потока, когда предполагается, что в направлении его движения смещение полностью отсутствует, а в направлении, перпендикулярном движению, происходит идеальное смешение. Гидродинамическая структура потоков, соответствующая модели идеального вытеснения, характерна для движения потоков в трубном пространстве кожухотрубчатых теплообменников различных конструкций, а также для теплообменного аппарата типа «труба в трубе».

Уравнение, описывающее изменение температуры в зоне идеального вытеснения, имеет вид:

, (7)

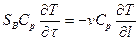
где S_b – сечение зоны идеального вытеснения; l – координата длины аппарата.

Диффузионная модель гидродинамической структуры потоков соответствует такому движению потоков, когда в направлении его движения существует продольное смещение, а перпендикулярном направлении предполагается наличие идеального смешения.

Диффузионная модель значительно лучше, чем модель идеального вытеснения, описывает гидродинамические условия в реальных кожухотрубчатых теплообменниках. Уравнение, характеризующее изменение температуры по длине зоны, имеет вид:

, (8)

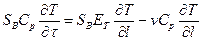
где е_т – коэффициент продольного переноса теплоты.

Температуры потоков в теплообменных аппаратах могут изменяться в каждой точке потока не только в результате его движения, но также из-за теплообмена с окружающей средой или за счет источника теплоты. Интенсивность источника теплоты записывается следующим образом:

где F – поверхность теплообмена, отнесенная к единице объема; К – коэффициент теплопередачи; DТ – разность температур.

Уравнения (4.6) и (4.7) для температур потока с учетом источника теплоты в потоке имеет вид:

;(10)

. (11)

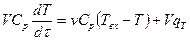
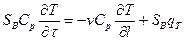
Учитывая (4.9) и зная, что V = S*L из (4.11) получим:

или

. (12)

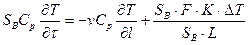
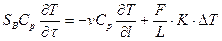
Аналогично для ДДМ с учетом (4.9) имеем:

. (13)

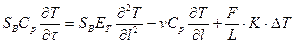
Для описания гидродинамической структуры потоков в реальных теплообменных аппаратах используются комбинированные модели движения потоков: ячеечная модель; модель идеального смешения с застойной зоной; модель идеального смешения с байпасом; последовательное соединение двух моделей МИС и МИВ. Применение таких моделей для описания гидродинамической структуры потоков позволяет описать изменение профиля температур как по длине, так и в объеме теплообменного аппарата.

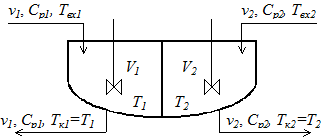
Теплообменник типа «перемешивание-перемешивание»

Математическая модель такого теплообменника (рис.4.2) представляет собой систему уравнений типа (4.7), записанных для теплоносителя и хладоагента:

, (14)

где T₁ – T₂ = DT, при этом T₁ и T₂ имеют постоянные значения в каждой точке объема идеального перемешивания V₁ и V₂; Т_вх1, Т_вх2 – температуры первичного и вторичного теплоносителей на входе в аппарат; Т_к1 = Т₂ и Т_к2 = Т₂ – конечные температуры первичного и вторичного теплоносителей. Величина FK(T₁ – T₂) имеет знак «минус» в уравнении описания потока теплоносителя, который отдает тепло, и знак «плюс», если тепло воспринимается теплоносителем.

Рис. 2. Схематическое изображение теплообменника типа «перемешивание-перемешивание»

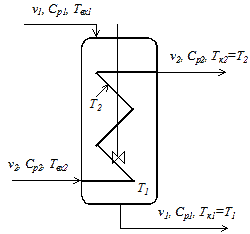
Теплообменник типа «перемешивание-вытеснение»

Математическая модель такого теплообменника (рис.4.3) включает уравнение модели идеального перемешивания для потока теплоносителя и уравнение модели идеального вытеснения для хладоагента:

;

, (15)

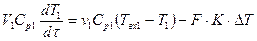
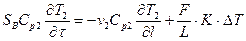
где DT = T₁ – T₂ при этом значения T₁ остается одинаковыми в каждой точке объема идеального перемешивания, а Т₂ изменяются по длине зоны идеального вытеснения.

Рис. 3. Схематическое изображение теплообменника типа «перемешивание — вытеснение»

Теплообменник типа «вытеснение-вытеснение»

Рассмотрим моделирование широко распространенного в химической технологии теплообменника «труба в трубе», структура потоков которого соответствует модели «вытеснение – вытеснение» (рис.3.1).

Рис.4. Схема теплообменника типа «труба в трубе»

Это так называемый прямоточный теплообменник, для которого модель имеет вид:

;

, (16)

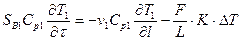
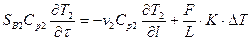
где DT = T₁ – T₂, при этом Т₁ и Т₂ изменяются по длине соответствующих зон идеального вытеснения. Цель работы: построить математическую модель и рассчитать теплообменный аппарат с известной структурой потоков.

Основные понятия и определения — температурное поле, градиент, тепловой поток, плотность теплового потока (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

1 Основные понятия и определения — температурное поле, градиент, тепловой поток, плотность теплового потока (q, Q), закон Фурье.

Температурное поле – совокупность значений температуры во всех точках изучаемого пространства для каждого момента времени.

ционарное – изменяется с течением времени. Стационарное – не изменяется.

Изотермическая поверхность – геометрическое место точек, имеющих в данный момент времени одинаковую температуру. Изотермические поверхности, соответствующие разным температурам, не могут пересекаться между собой. Они могут замыкаться сами на себя либо оканчиваться на поверхности тела.

Градиент температуры – вектор, направленный по нормали к изотермическиой поверхности в сторону возрастания температуры.

Количество теплоты, Вт, проходящей в единицу времени через изотермическую поверхность площадью F, называется тепловым потоком и определяется из выражения: .

Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности , Вт/м2, называется плотностью теплового потока: .

Связь между количеством теплоты dQ, Дж, которое за время dt проходит через элементарную площадку dF, расположенную на изотермической поверхности, и градиентом температуры dt/dn устанавливается законом Фурье: .

2. Уравнение теплопроводности, условия однозначности.

Дифференциальное уравнение теплопроводности выведено со следующими допущениями:

— тело однородно и изотропно;

— физические параметры постоянны;

— деформация рассматриваемого объема, связанная с изменением температуры, очень мала по сравнению с самим объемом;

— внутренние источники теплоты в теле, которые в общем случае могут быть заданы как , распределены равномерно.

, или .

Дифференциальное уравнение теплопроводности устанавливает связь между временным и пространственным изменениями температуры в любой точке тела, в которой происходит процесс теплопроводности.

Если принять теплофизические характеристики постоянными, что предполагалось при выводе уравнения, то дифур принимает вид: .

Примем — коэффициент температуропроводности.

и , где — оператор Лапласса в декартовой системе координат.

Тогда .

Условия однозначности или краевые условия включают в себя:

3. Теплопроводность в стенке (граничные условия 1-ого рода).

Теплопроводность однослойной стенки.

Рассмотрим однородную плоскую стенку толщиной d. На наружных поверхностях стенки поддерживаются постоянные во времени температуры tc1 и tc2. Теплопроводность материала стенки постоянна и равна l.

При стационарном режиме , кроме того, температура изменяется только в направлении, перпендикулярном плоскости стеки (ось 0х): . Поэтому уравнение теплопроводности имеет вид: .

Постоянные С1 и С2 в уравнении определим из граничных условий I рода:

при х = 0: t = tc1 и C2 = tc1;

при х = d: t = tc2 и C1 = –(tc1 – tc2)/ d.

Следовательно:

Определим плотность теплового потока через плоскую стенку. В соответствии с законом Фурье с учетом равенства (*) можно написать: .

Следовательно (**).

Разность значений температуры в уравнении (**) называется температурным напором. Из этого уравнения видно, что плотность теплового потока q изменяется прямо пропорционально теплопроводности l и температурному напору Dt и обратно пропорционально толщине стенки d.

Отношение называется тепловой проводимостью стенки, а обратная ему величина – термическим сопротивлением стенки.

Общее количество теплоты, которое передается через поверхность стенки площадью F за промежуток времени t: .

Теплопроводность l следует брать при средней температуре стенки.

Теплопроводность многослойной стенки.

Для каждого слоя :; ; .

Определяем температурные напоры:

Для сравнения теплопроводящих свойств многослойной плоской стенки со свойствами однородных материалов вводят понятие эквивалентной теплопроводности. Это – теплопроводность однослойной стенки, толщина которой равна толщине рассматриваемой многослойной стенки, т. е. при условии, что разности температур на поверхностях однослойной и многослойной стенок и тепловые потоки одинаковы. Эквивалентная теплопроводность определяется из следующего выражения:

4. Теплопередача через плоскую стенку (граничные условия 3-его рода).

Передача теплоты от одной подвижной среды (жидкости или газа) к другой через разделяющую их твердую стенку любой формы называется теплопередачей. Особенности протекания процесса на границах стенки при теплопередаче характеризуется граничными условиями III рода, которые задаются значениями температуры жидкости с одной и другой стороны стенки, а также соответствующими значениями коэффициентов теплоотдачи.

Рассмотрим стационарный процесс теплопередачи через бесконечную однородную плоскую стенку толщиной d. Задана теплопроводность стенки l, температуры окружающей среды tж1 и tж2, коэффициенты теплоотдачи a1 и a2. Необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхностях стенки tc1 и tc2. Плотность теплового потока от горячей среды к стенке определится уравнением: . Этот же тепловой поток передается путем теплопроводности через твердую стенку: и от второй поверхности стенки к холодной среде: .

Тогда ,

где – коэффициент теплопередачи, числовое значение k выражает количество теплоты, проходящей через единицу поверхности стенки в единицу времени пр разности температур между горячей и холодной средой 1К и имеет туже единицу измерения, что и коэффициент теплоотдачи, Дж/(с*м2К) или Вт/(м2К).

Величина, обратная коэффициенту теплопередачи называется термическим сопротивлением теплопередаче: .

термическое сопротивление теплоотдаче;

термическое сопротивление теплопроводности.

Для многослойной стенки .

Плотность теплового потока через многослойную стенку: .

Тепловой поток Q, Вт, проходящий через плоскую стенку с площадью поверхности F, равен: .

Температура на границе любых двух слоев при граничных условиях III рода может быть определена по уравнению . Также можно определить температуру графическим методом.

5. Теплопроводность в цилиндрической стенке (граничные условия 1-ого рода).

Рассмотрим стационарный процесс теплопроводности через однородную цилиндрическую стенку (трубу) длиной l с внутренним радиусом r1 и наружным r2. Теплопроводность материала стенки l – величина постоянная. На поверхности стенки заданы постоянные температуры tc1 и tc2.

В случае (l>>r) изотермические поверхности будут цилиндрическими, а температурное поле одномерным. Т. е. t=f(r), где r – текущая координата цилиндрической системы, r1£r£r2. Тогда уравнение теплопроводности, которое для плоской стенки имело вид , для цилиндрической примет следующую форму: .

Введение новой переменной позволяет привести уравнение к виду:.

Граничные условия I рода записываются равенствами:

при r = r1: t = tc1;

при r =r2: t = tc2.

Подставляя эти выражения в равенство , имеем:

;

Подставляя значения С1 и С2 в уравнение , получим:

Это выражение представляет собой уравнение логарифмической кривой. Следовательно, внутри однородной цилиндрической стенки при постоянном значении теплопроводности температура изменяется по логарифмическому закону.

Для нахождения количества теплоты, проходящего через цилиндрическую стенку поверхность площадью F в единицу времени, можно воспользоваться законом Фурье:

Подставляя в уравнение закона Фурье значение градиента температуры согласно уравнению получим: (*) ® величина Q зависит не от толщины стенки, а от отношения его внешнего диаметра к внутреннему.

Если отнеси тепловой поток, отнесенный к единице длины цилиндрической стенки, то уравнение (*) можно записать в виде .

Тепловой поток, отнесенный к единице длины трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Величина есть термическое сопротивление теплопроводности цилиндрической стенки.

Для многослойной цилиндрической стенки.

Температура на границе двух любых слоев равна: .

6. Теплопередача через цилиндрическую стенку (граничные условия 3-его рода).

Рассмотрим однородную цилиндрическую стенку большой длины с внутренним диаметром d1, наружным диаметром d2 и постоянной теплопроводностью. Заданы значения температуры горячей tж1 и холодной tж2 среды и коэффициенты теплоотдачи a1 и a2. для стационарного режима можно записать:

;;

где — линейный коэффициент теплопередачи, характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку; численно равен количеству теплоты, которое проходит от одной среды к ругой через стенку трубы длиной 1м в единицу времени при разности температур между ними в 1К.

Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередаче.

Для многослойной стенки линейное термическое сопротивление теплопередаче складывается из линейных сопротивлений теплоотдаче и суммы линейных термических сопротивлений теплопроводности слоев.

Температуры на границе между слоями:

7. Шаровая стенка (граничные условия 1-ого и 3-его рода).

Граничные условия III рода.

Принципы теплопередачи через шаровую стенку те же, что и через цилиндрическую. Пусть внутренний диаметр шара равен d1, внешний – d2, теплопроводность l, температура горячей жидкости внутри шара tж1, температура холодной жидкости снаружи шара tж2, коэффициенты теплоотдачи a1 и a2.

При стационарном режиме количество теплоты, переданное от горячей жидкости к холодной, равно: ;;

где – коэффициент теплопередачи для шаровой стенки.

Величина, обратная коэффициенту теплопередачи шаровой стенки, называется термическим сопротивлением теплопередаче шаровой стенки.

Граничные условия I рода.

Пусть имеется шар с радиусами внутренней и внешней поверхности r1 и r2, постоянной теплопроводностью и с заданными равномерно распределенными температурами поверхностей tc1 и tc2.

При этих условиях температура зависит только от радиуса r. По закону Фурье тепловой поток сквозь шаровую стенку равен: .

Интегрирование уравнения дает следующее распределение температуры в шаровом слое:

Граничные условия.® ;

Следовательно , d — толщина стенки.

Распределение температуры: ® при постоянной теплопроводности температура в шаровой стенке изменяется по закону гиперболы.

8. Термические сопротивления.

Однослойная плоская стенка:

Граничные условия 1го рода

Граничные условия 3го рода

Величина, обратная коэффициенту теплопередачи называется термическим сопротивлением теплопередаче: .

Однослойная цилиндрическая стенка:

Граничные условия 1го рода

Величина есть термическое сопротивление теплопроводности цилиндрической стенки. (для многослойной стенки: )

Граничные условия 3го рода

Линейное термическое сопротивление теплопередаче:

Линейное термическое сопротивление теплопередаче:

(многослойная стенка)

9. Критический диаметр изоляции.

Рассмотрим случай когда труба покрыта однослойной тепловой изоляцией с наружным диаметром d3. считая заданными и постоянными коэффициенты теплоотдачи a1 и a2, температуры обеих жидкостей tж1 и tж2, теплопроводности трубы l1 и изоляции l2.

Согласно уравнению , выражение для линейного термического сопротивления теплопередаче через двухслойную цилиндрическую стенку имеет вид: .

При возрастании диаметра изоляции член будет возрастать, а член – уменьшаться. Иными словами, увеличения наружного диаметра изоляции влечет за собой увеличение термического сопротивления теплопроводности изоляции и уменьшение термического сопротивления теплоотдаче на ее наружной поверхности. Последнее обусловлено увеличением площади наружной поверхности.

Экстремум функции Rl – – критический диаметр обозначается как dкр. Служит показателем пригодности материала к использованию его в качестве тепловой изоляции для трубы с заданным наружным диаметром d2 при заданном коэффициенте теплоотдачи a2.

10. Выбор тепловой изоляции по критическому диаметру.

См. вопрос 9. диаметр изоляции должен превышать критический диаметр изоляции.

11. Теплопередача через оребренную стенку. Коэффициент оребрения.

Рассмотрим оребренную стенку с толщиной d и теплопроводностью l. С гладкой стороны площадь поверхности равна F1, а с оребренной – F2. заданы постоянные во времени температуры tж1 и tж2, а также коэффициенты теплоотдачи a1 и a2.

Обозначим температуру гладкой поверхности tc1. Предположим, что температура поверхностей ребер и самой стенки одинакова и равна tc2. Такое предположение, вообще говоря, не соответствует действительности, но упрощает расчеты и им часто пользуются.

При tж1 > tж2 для теплового потока Q можно написать следующие выражения:

;;

где – коэффициент теплопередачи для оребренной стенки.

При расчете плотности теплового потока на единицу неоребренной поверхности стенки получим: . k1 – коэффициент теплопередачи, отнесенный к неоребренной поверхности стенки.

Отношение площади оребренной поверхности к площади гладкой поверхности F2/F1 называется коэффициентом оребрения.

12. Нестационарная теплопроводность. Направляющая точка. Физический смысл Bi, Fo.

Нестационарная теплопроводность – процесс при котором температура в заданной точке твердого тела изменяется во времению совокупность указанных температур образует нестационарное температурное поле, нахождение которого и является основной задачей нестационарной теплопроводности. Процессы нестационарной теплопроводности имеют большое значение для отопления, вентиляции, кондиционирования воздуха, теплоснабжения и теплогенерирующих установок. Ограждения зданий испытывают изменяющиеся во времени тепловые воздействия как со стороны наружного воздуха, так и со стороны помещения таким образом в массиве ограждающей конструкции осуществляется процесс нестационарной теплопроводности. Задачу об отыскании трехмерного температурного поля можно сформулировать в соответствии принципами, изложенными в разделе «математическая формулировка задач теплообмена». Формулировка задачи включает уравнение теплопроводности: , где – коэффициент температуропроводности м2/с, а также условия однозначности, позволяющие выделить единственное решение из множества решений уравнения, различающихся значением констант итегрирования.

Условия однозначности включают начальные и граничные условия. Начальные условия задают значения искомой функции t в начальный момент времени по всей области D. В качестве области D, в которой необходимо найти температурное поле, будем рассматривать прямоугольный параллелепипед с размерами 2d, 2ly, 2lz, например, элемент строительной конструкции. Тогда начальные условия можно записать в виде: при t =0 и — d£х£d; — ly£у£ly; -lz£z£lz имеем t = t(x, y, z,0) = t0(x, y, z). Из этой записи видно, что начало декартовой сстемы координат расположено в центре симметрии параллелепипеда.

Граничные условия сформулируем в форме граничных условий III рода, часто встречающихся на практике. Граничные условия III рода задают для любого момента времени на границах области D коэффициент теплоотдачи и температуру окружающей среды. В общем случае на различных участках поверхности S области D эти величины могут быть различными. Для случая одинакового коэффициента теплоотдачи a на всей поверхности S и всюду одинаковой температуры окружающей среды tж граничные условия III рода при t >0 можно записать в виде: ; ;

где . S – поверхность, ограничивающая область D.

Температура в каждом из трех уравнений берется на соответствующей грани параллелепипеда.

Рассмотрим аналитическое решение сформулированной выше задачи в одномерном варианте, т. е. при условии ly, lz »d. В этом случае требуется найти температурное поле вида t = t(x, t). Запишем формулировку задачи:

уравнение ;

начальное условие: при t = 0 имеем t(x, 0) = t0 = const;

граничное условие: при x = ±d, t > 0 имеем .

В соответствии с этими выражениями имеется бесконечная пластина толщиной 2d, изготовленная из материала с коэффициентом темературопроводности а и обладающая в начальный момент времени температурой t0. пластина резко переносится в среду с температурой tж и коэффициентом теплоотдачи a. С этого момента температура в пластине изменяется так, чтобы удовлетворялось уравнение . Задача состоит в том, чтобы получить конкретную формулу t = t(x, t), позволяющую найти температуру t в любой точке пластины в произвольный момент времени.

Сформулируем задачу в безразмерных переменных, это позволит сократить записи и сделает решение более универсальным. Безразмерная температура равна , безразмерная координата равна Х = х/d. Подставив эти величины в уравнение получим , где — число Фурье (безразмерное время).

Начальное условие запишется в следующем виде: Fo = 0; Q = 1.

Граничное условие запишется как: Fo > 0; Х =1; , где – число Био.

Формулировка задачи в безразмерном виде содержит единственный параметр – число Био, которое в данном случае является критерием, так как составлено только из величин, входящих в условие однозначности. Использование числа Био связано с нахождением температурного поля в твердом теле, поэтому в знаменателе Bi – теплопроводность твердого тела. Bi – наперд заданный параметр и является критерием.

Если рассматривать 2 процесса нестационарной теплопроводности с одинаковыми числами Био, то, согласно третьей теореме подобия, эти процессы подобны. Это значит, что в сходственных точках (т. е. при Х1=Х2; Fo1=Fo2) безразмерные температуры будут численно равны: Q1=Q2. следовательно, произведя один расчет в безразмерном виде, мы получим результат, справедливый для класса подобных явлений, которые могут различаться размерными параметрами a, l, d, t0 и tж.

13. Нестационарная теплопроводность для неограниченной плоской стенки.

17. Уравнение энергии. Условия однозначности.

Уравнение энергии описывает процесс переноса теплоты в материальной среде. При этом ее распространение связано с превращением в другие формы энергии. Закон сохранения энергии применительно к процессам ее превращения формулируется в виде первого закона термодинамики, который и является основой для вывода уравнения энергии. Среда, в которой распространяется теплота, предполагается сплошной; она может быть неподвижной или движущейся. Поскольку случай движущейся среды является более общим, используем выражение первого закона термодинамики для потока: (17.1), где q – подводимая теплота, Дж/кг; h – энтальпия, Дж/кг; w – скорость среды в рассматриваемой точке, м/с; g – ускорение свободного падения; z – высота, на которой расположен рассматриваемый элемент среды, м; lтр – работа против сил внутреннего трения, Дж/кг.

В соответствии с уравнением 17.1 подводимая теплота затрачивается на увеличение энтальпии, кинематической энергии и потенциальной энергии в поле сил тяжести, а также на совершение работы против вязких сил. Работа трения преобразуется в теплоту, представляющую собой часть подводимой теплоты: , где dqто – теплота, подводимая в результате теплообмена со средой, окружающей рассматриваемый элемент жидкости; dqтр – теплота, выделяющаяся при работе сил внутреннего трения.

Следовательно уравнение 17.1 можно представить следующим образом: (17.2).

Т. к. (17.3).

Подсчитаем количество подводимой и отводимой теплоты в единицу времени для элемента среды в виде прямоугольного параллелепипеда, размеры которого достаточно малы для того, чтобы в его пределах можно было бы предположить линейное изменение плотности теплового потока. По оси 0х в левую грань элемента за единицу времени подводится количество теплоты , из правой грани отводится: ; их разность равна .

Проводя аналогичную операцию для осей 0y и 0z, получим соответственно разности: ; . Просуммировав все три разности получим результирующее количество теплоты, подводимое(или отводимое) в элемент за единицу времени.

источники:

http://helpiks.org/4-42852.html

http://pandia.ru/text/78/654/64363.php