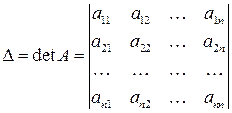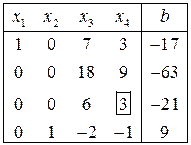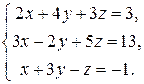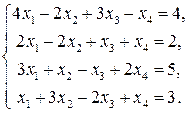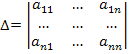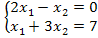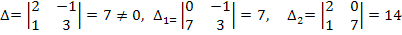Решение невырожденных линейных систем.
Л е к ц и и 3-4
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Основные понятия.
Решение систем линейных уравнений. Теорема
Кронекера-Капелли.
Решение невырожденных линейных систем. Формулы
Крамера.
Решение систем линейных уравнений методом Гаусса.
Системы линейных однородных уравнений.
Основные понятия
Системой линейных алгебраических уравнений (СЛАУ), содержащей mуравнений и n неизвестных, называется система вида
 |
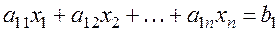

где числа аij, 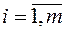

Такую систему удобно записывать в компактной матричной форме
А · Х = В.
Здесь А — матрица коэффициентов системы, называемая основной матрицей:


Произведение матриц А ·X определено, так как в матрице А столбцов столько же, сколько строк в матрице X ( n штук ).
Расширеннойматрицей системы называется матрица 

Решениемсистемы называется n значений неизвестных х1 = c1, x2 = c2, . . . , xn = cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца 
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
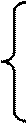 |


Однородная система всегда совместна, так как х1 = х2 = . . . = хn = 0 является решением системы. Это решение называется нулевым или тривиальным.
Решение систем линейных уравнений.
Теорема Кронекера-Капелли



Исчерпывающий ответ на вопрос о совместности этой системы дает теорема Кронекера-Капелли.
Теорема 1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Примем ее без доказательства.
Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Решение невырожденных линейных систем.
Формулы Крамера.



или в матричной форме А • X = В.
Основная матрица Атакой системы квадратная. Определитель этой матрицы
называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.
Найдем решение данной системы уравнений в случае Δ ≠ 0 .
Умножив обе части уравнения А • X = В слева на матрицу A -1 , получим A -1 • А • Х = A -1 • B . Поскольку A -1 • А = Е и Е • X = X, то
X = A -1 • B . (1)
Отыскание решения системы по формуле (1) называют матричным способом решения системы.
Матричное равенство (1) запишем в виде


Отсюда следует, что


Но 
по элементам первого столбца. Определитель Δ получается из определителя Δ путем замены первого столбца коэффициентов столбцом из свободных членов.
Итак, 
Аналогично: 


. . . , 

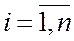
называются формулами Крамера.
Итак, невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом (1) либо по формулам Крамера (2).
 |
Пример. Решить систему 2x1 – x2 = 0 ,
Решение: 




Решение произвольных систем линейных уравнений
Тема 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
1. Матрицы. Сложение матриц; умножение матрицы на число; произведение матриц. Обратная матрица.
2. Определители n-го порядка и их свойства. Методы вычисления определителей.
3. Обратная матрица.
5. Решение невырожденных систем линейных уравнений.
6. Теорема Кронекера – Капелли. Решение произвольных линейных систем.
Решение невырожденных систем линейных уравнений
Пусть задана система линейных уравнений

где 


Решением системы (1.1) называется такое множество значений неизвестных 
Система уравнений, имеющая хотя бы одно решение, называется совместной, а система, не имеющая решений – несовместной.

называются матрицей системы и расширенной матрицей системы соответственно.
Рассмотрим случай, когда число уравнений m системы совпадает с числом неизвестных n (m = n). Тогда матрица системы А является квадратной матрицей порядка n.
Система n уравнений с n неизвестными называется невырожденной, если определитель матрицы системы А отличен от нуля ( 
Невырожденная система имеет единственное решение. Существует два метода решения таких систем.
1. Правило Крамера. Если определитель Δ отличен от нуля, то решение системы находится по формулам

где 
2. Матричный метод. Введем матрицу столбец свободных членов системы 

Тогда систему n уравнений с n неизвестными можно записать в виде

Эта форма записи системы называется матричной.
Матрицей 


где Е – единичная матрица n-го порядка.
Матрица, определитель которой не равен нулю, называется невырожденной.
Для того чтобы данная матрица имела обратную, необходимо и достаточно, чтобы она была невырожденной.
Рассмотрим уравнение (1.3). Пусть А – невырожденная матрица. Тогда решение системы можно найти по формуле

Пример 1.1. Проверить невырожденность системы линейных уравнений 
Решение. Запишем матрицу системы 

Так как 
а) по формулам Крамера.

По формулам (1.2) находим решение системы:
Делаем проверку: 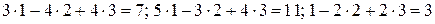
б) матричным методом.
Находим обратную матрицу

где 




где 




По формуле (1.4) находим решение:

Ответ: 
Решение произвольных систем линейных уравнений
Рассмотрим произвольную систему линейных уравнений (1.1).
Элементарными преобразованиями матрицы называются:
а) перестановка местами любых двух строк;
б) умножение строки на некоторое число 
в) прибавление к одной строке матрицы любой другой строки, умноженной на некоторое число;
г) удаление нулевой строки.
Решение системы методом Жордана–Гаусса основано на следующем утверждении: элементарные преобразования расширенной матрицы системы не изменяют множества решений системы.
Суть метода заключается в том, чтобы при помощи элементарных преобразований привести расширенную матрицу к наиболее простому виду.
С помощью операции в) можно исключить какое-либо неизвестное из всех уравнений, кроме одного.
Переменная 


Матрица системы с помощью элементарных преобразований приводится к так называемому базисному виду, если в каждом уравнении системы есть базисная переменная.
Если матрица системы приведена к базисному виду, то переменные, не являющиеся базисными, называются свободными.
Решение системы, полученное после приравнивания нулю всех свободных переменных, называется базисным.
Опишем одну итерацию метода Жордана–Гаусса.
В первой строке расширенной матрицы находим ненулевой элемент 


Элемент 
Если 


После этой операции коэффициент при 

Описанную итерацию проводим для остальных строк расширенной матрицы, пока не получим m базисных неизвестных ( в каждом уравнении – по одной базисной переменной).
После этого находим общее решение и базисное (приравнивая свободные неизвестные нулю).
Пример 1.2. Решить систему линейных уравнений
методом Жордана–Гаусса. Найти общее и базисное решения.
Решение. Вычисления будем производить в таблице. В исходной части таблицы записываем расширенную матрицу системы.
В первой строке выберем элемент 

Выбираем элемент 
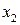
Выбираем, например, элемент 

Теперь делаем нули в остальных строках четвертого столбца. Получаем таблицу, в которой переменная 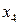
Удаляем вторую нулевую строку, получаем таблицу

Поскольку каждое уравнение теперь содержит по одной базисной переменной, то оставшаяся небазисная переменная 
Полагаем 

Из второй строки следует 


Из первой строки следует 


Выписываем общее решение: 
Найдем базисное решение. Положим 

Сделаем проверку, подставляя найденное решение в исходную систему
Ответ. Общее решение: 

Задание 1. Проверить невырожденность системы линейных уравнений и решить ее: а) по формулам Крамера; б) матричным методом.
1.1. 

1.4. 

1.7 

1.10. 
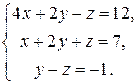
1.13. 

1.16. 
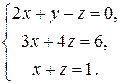
1.19. 

1.22. 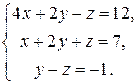

1.25. 
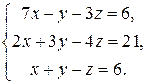
1.28. 

Задание 2. Решить систему линейных уравнений методом Жордана–Гаусса. Найти общее и базисное решения.
2.1. 
2.3. 
2.5. 
2.7. 
2.9. 
2.11. 
2.13. 
2.15. 
2.17. 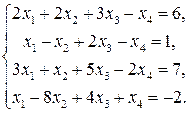
2.19. 
2.21. 
2.23. 
2.25. 
2.27. 
2.29. 
Решение невырожденных линейных систем.
Пусть дана система п линейных уравнений с п неизвестными
или в матричной форме А * Х = В.
Основная матрица А такой системы квадратная. Определитель этой матрицы
называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.
Найдём решение данной системы уравнений в случае ∆ ≠ 0.
Умножив обе части уравнения А * Х = В слева на матрицу А -1 , получим А -1 * А * Х = А -1 * В. Поскольку А -1 * А = Е и Е * Х = Х, то Х = А -1 * В.
Отыскание решения системы по формуле (4.1) называют матричным способом решения системы.
Матричное равенство (4.1) запишем в виде

то есть
Отсюда следует, что
по элементам первого столбца. Определитель ∆1 получается из определителя ∆ путём замены первого столбца коэффициентов столбцом из свободных членов.





называются формулами Крамера.
Итак, невырожденная система п линейных уравнений с п неизвестными имеет единственное решение, которое может быть найдено матричным способом (4.1) либо по формулам Крамера (4.2).
Пример 4.3. Решить систему
Решение:
Значит,
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какой вид имеет система линейных алгебраических уравнений?
2. Как записать систему линейных алгебраических уравнений в матричной форме?
3. Сформулируйте теорему Кронекера-Капелли.
4. Какая система уравнений называется совместной (несовместной)?
5. Что значит решить систему линейных алгебраических уравнений?
6. Сформулируйте правила решения произвольной системы линейных алгебраических уравнений.
7. Сформулируйте правила решения систем с помощью обратной матрицы.
8. Сформулируйте правила решения систем методом определителя (формулы Крамера).
http://allrefrs.ru/5-46662.html
http://mydocx.ru/12-61740.html