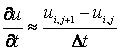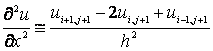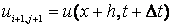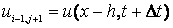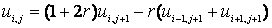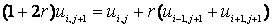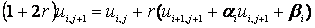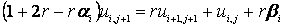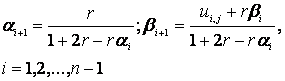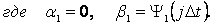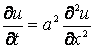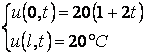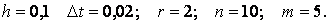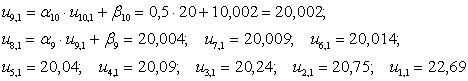Неявная разностная схема для уравнения

Неявная разностная схема для уравнения

3.4.2. Неявная разностная схема

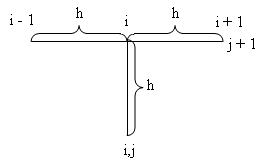
Из сеточной области х = ih , t = jΔt возьмём шаблон типа:

Запишем разностные отношения для производных

;

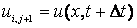
Получим неявную разностную схему:

Схема называется неявной, так как число неизвестных переменных превышает число известных.

Неявная разностная схема решается методом прогонки, суть которого состоит в следующем:

Запишем рекуррентные соотношения вида:

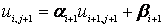
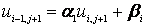
Исключим одну неизвестную переменную из выражения (4), подставив в него (6)

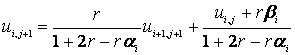
Выражения (5) и (7) тождественны. Вычисление коэффициентов α _{i +1} и β_{i +1} c оставляют прямой ход прогонки:

Обратный ход прогонки определяется формулой (5). Здесь индекс пробегает все значения от n -1, n -2,…,1.

Пример. Для стержня, длинной 1м, найти распределение температуры в течение 0,1 часа, если конец стержня нагревается (его температура изменяется во времени по линейному закону), температура другого конца практически остаётся постоянной. В начальный момент времени температура стержня одинакова во всех точках. Коэффициент температуропроводности равен 1. Исходное уравнение:

Пусть

Начальное условие и его разностный аналог и( х,0) = и _{i ,0} = 20.

Разностные аналоги граничных условий:

Конечно-разностная сетка приведена на рис. 3.4.

Прямой ход прогонки:

Обратный ход прогонки:

Таким же образом рассчитываются температуры по длине стержня для моментов времени:

Разностный метод для уравнения колебаний

8.1. Разностный метод для уравнения колебаний

8.1.1. Уравнение колебаний струны. Явная схема

Рассмотрим задачу о малых колебаниях натянутой струны с распределенной по длине нагрузкой f(x, t) (см. рис. 8.1):

(8.11)

(8.12)

(8.13)

Струна совершает плоские колебания, т. е. точки струны перемещаются параллельно плоскости t = 0.

Функция u(x, t) выражает смещение точки x струны в момент времени t от прямолинейной формы.

Начальные условия (8.12) означают следующее. Форма струны в начальный момент времени t = 0 выражается функцией μ(x). Скорость перемещения точки x струны в момент времени t = 0 равна значению функции μ0(x).

Краевые условия (8.13) говорят о том, что левый конец струны с течением времени совершает смещение μ1(t), а правый конец — смещение μ2(t).

Если концы струны закреплены, то μ1(t) = μ2(t) = 0.

Мы предполагаем, что начальные условия (8.12) и краевые условия (8.13) должны быть согласованы между собой в угловых точках, т. е. выполнены условия .

На рис. 8.1 представлен случай, когда , .

Введем сеточную область (рис.8.2, a)). В прямоугольной области зададим точки:

(8.14)

Рассмотрим уравнение (8.11) в точках , , , и заменим производные разностными формулами

, (8.15)

Обозначим через приближенные значения искомой функции в точках . Тогда из уравнения (8.11) получим разностное уравнение (разностную схему), которое аппроксимирует уравнение (8.11) с порядком O(h2 + τ2):

(8.16)

На рис. 8.2 b) изображен шаблон «крест» разностного уравнения (8.16). Разностное уравнение (8.16) связывает значения неизвестной функции на трех слоях (k – 1, k, k + 1).

На слое k = 0 заданы начальные условия (8.12), из которых следует, что

. (8.17)

Чтобы найти значения неизвестной функции на слое k = 1, используем условие для производной ut(x, 0) из (8.12). Для этого построим разложение в ряд Тейлора

. (8.18)

Из уравнения (8.11), учитывая первое условие в (8.12), выразим вторую производную

. (8.19)

Теперь, учитывая условие в (8.12), из (8.18), (8.19) выводим формулу для вычисления значений функции на первом слое:

. (8.20)

С учетом (8.13), окончательно получим для приближенных значений искомой функции на первом слое формулы

. (8.21)

Учитывая граничные условия (8.13) из (8.16) выводим формулы для вычисления значений на слоях :

(8.22)

Мы получили явные формулы (8.17), (8.21), (8.22) решения разностной задачи.

Разностная схема называется устойчивой, если она имеет единственное решение и малым изменениям исходных данных отвечают малые изменения решения.

Приведем без доказательства (доказательство можно найти в [9]) следующий факт: для выполнения условия устойчивости разностной схемы (8.16) необходимо и достаточно, чтобы выполнялось условие Куранта cτ 0 находим методом прогонки, последовательными вычислениями в несколько этапов.

2.1. Вычислим правые части (8.26):

(8.29)

2.2. Вычислим прогоночные коэффициенты:

(8.30)

(8.31)

(8.32)

2.3. Вычислим решение ui,k+1:

(8.33)

(8.34)

Отметим преимущества неявной схемы перед явной схемой:

В явной схеме надо выбирать шаги h и τ так, чтобы выполнялось условие устойчивости (условие Куранта) cτ

Неявная разностная схема для уравнения

Запишем аппроксимацию начального и граничных условий :

Аппроксимация граничных условий (4.7) записана на ( n + 1)-ом шаге по времени для удобства последующего изложения метода и алгоритма решения неявной разностной схемы (4.6).
В разделе » Порядок аппроксимации разностной схемы » было отмечено, что разностная схема (4.6) имеет такой же порядок аппроксимации , как и соответствующая ей явная разностная схема (4.2) , а именно:

В разделе » Доказательство абсолютной устойчивости неявной разностной схемы » было доказано, что неявная разностная схема (4.6) абсолютно устойчива, т.е. вне зависимости от выбора интервала деления на разностной сетке (или, иначе говоря, выбора расчётного шага по независимым переменным) погрешность решения неявной разностной схемы в процессе вычислений возрастать не будет. Отметим, что это, безусловно, является достоинством неявной разностной схемы (4.6) по сравнению с явной разностной схемой (4.2) , которая устойчива только при выполнения условия (3.12) . В то же время явная разностная схема имеет достаточно простой метод решения , а метод решения неявной разностной схемы (4.6), называемый методом прогонки , более сложен. Прежде чем перейти к изложению метода прогонки , необходимо вывести ряд соотношений , используемых этим методом.

Характеристика явной разностной схемы.

Рассмотрим одномерное дифференциальное уравнение параболического типа с начальным и граничными условиями :

Запишем для уравнения (4.1) явную разностную схему :

Запишем аппроксимацию начального и граничных условий :

Аппроксимация граничных условий (4.3) записана на ( n + 1)-ом шаге по времени для удобства последующего изложения метода и алгоритма решения явной разностной схемы (4.2).
В разделе » Порядок аппроксимации разностной схемы » было доказано, что разностная схема (4.2) имеет порядок аппроксимации :

В разделе » Доказательство условной устойчивости явной разностной схемы » было получено условие устойчивости данной разностной схемы, накладывающее ограничение на выбор интервала деления при создании разностной сетки (или, иначе говоря, ограничение на выбор расчётного шага по одной из независимых переменных):

Отметим, что это, безусловно, является недостатком явной разностной схемы (4.2). В то же время она имеет достаточно простой метод решения .