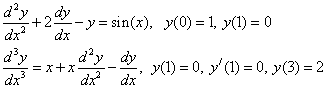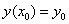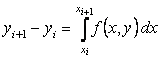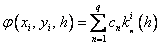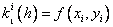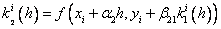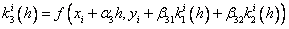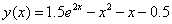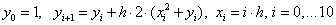Неявные методы решения дифференциальных уравнений
1. Неявные методы
Методы численного решения ОДУ, с которыми мы познакомились в первом разделе этого курса (метод Эйлера, метод средней точки и т. п.), называются «явными» методами. Однако иногда система ОДУ может стать «жесткой», а решать такие системы явными методами неудобно. В этом случае желательно изменить формулировку задачи так, что не пришлось иметь дело с жесткой системой. Но это не всегда возможно, поэтому вы должны уметь решать жесткие ОДУ. Для этого, как правило, используют методы решения, которые называются «неявными».
2. Пример жесткого ОДУ
Во-первых, в чем смысл и причина появления жестких уравнений? Давайте рассмотрим пример, который часто возникает в динамике. Предположим, что у нас есть частица, с координатами \((x(t),y(t))\) , и предположим, что мы хотим, чтобы ее \(y\) -координата всегда оставалась равной нулю. Один из способов добиться этого — добавить слагаемое \(-ky(t)\) , к производной \(\dot
(Кроме того, мы предполагаем, что частица не запускается из \(y_0=0\) ). В результате частица будет сильно притягиваться к прямой \(y = 0\) , и менее сильно — к \(x = 0\) . Если решать ОДУ на достаточно продолжительном интервале времени, то частица рано или поздно попадет в точку \((0, 0)\) и останется в ней.
Теперь предположим, что для решения уравнения мы используем метод Эйлера. Если сделать шаг размера \(h\) , то получим
Если мы посмотрим на \(у\) -компоненту этого уравнения, то увидим, что при \(|1-hk|>1\) , вычисленное нами \(y_
Теперь, если \(k\) – большое число, мы вынуждены делать очень маленькие шаги. Это означает, что частица будет двигаться к \((0,0)\) мучительно медленно. Даже если взять \(y_0\) очень близким к нулю, то придется делать настолько маленькие шаги, что изменение \(x\) -координаты будет практически незаметно. Вот так выглядит жесткое ОДУ. В данном случае жесткость возникает из-за слишком большого \(k\) , призванного удержать частицу возле прямой \(у = 0\) . Позже, когда мы будем рассматривать частицы, соединенные пружинами, мы увидим то же самое явление: от жесткости пружины и происходит термин «жесткое» ОДУ. Даже если мы используем более совершенный численный метод, такой как метод Рунге-Кутта 4-го порядка, это лишь слегка улучшит ситуацию с выбором величины шага, но мы все равно будем иметь серьезные вычислительные проблемы.
Теперь, как мы уже говорили выше, нужно попытаться переформулировать свою задачу так, чтобы избежать появления жесткого ОДУ. Если же это не получится, то нужно использовать неявный метод решения ОДУ. Метод, который мы покажем ниже, является самым простым из неявных методов. Он основан на том, что шаг обычного метода Эйлера выполняется «наоборот».
3. Решение жесткого ОДУ
Пусть дано дифференциальное уравнение
Формула явного метода Эйлера
продвигает систему вперед на шаг \(h\) во времени. Для жестких систем, однако, удобнее заменить эту формулу на следующую
То есть, нам нужно вычислить \(f\) в точке, в которую мы стремимся попасть ( \(\textbf
Чтобы справиться с этим, заменим \(f (\textbf
Теперь заменим \(f(\textbf
(Заметим, что поскольку \(f(\textbf
Разделим обе части последнего соотношения на \(h\) и перепишем результат в виде
где \(I\) — единичная матрица.
Разрешая это соотношение относительно \(\Delta\textbf
Вычисление \(\textbf
Применим теперь неявный метод для решения уравнения \eqref
Дифференцирование по \(\textbf
Тогда матрица \((1/h)\textbf — f^<\prime>(\textbf
Обращая эту матрицу и умножая на \(f(\textbf
Какова же предельная длина шага в этом случае? Ответ: нет предела! Если позволить \(h\) расти до бесконечности, мы получаем следующее
Это означает, что мы достигнем \(\textbf
4. Решение уравнений второго порядка
Большинство задач динамики записывается в виде ДУ 2-го порядка
Это уравнение легко преобразуется систему ДУ 1-го порядка, добавлением новых переменных. Если мы определим \(\textbf
что представляет собой систему ДУ 1-го порядка. Однако, применяя обратный (неявный) метод Эйлера к уравнению \eqref
Система \(n \times n\) , которая должна быть решена, получается следующим образом. Введем для краткости следующие обозначения \(\textbf
Применяя к \(f\) разложение в ряд Тейлора, которое в данном контексте является функцией и \(\textbf
В этом уравнении, производная \(\partial f / \partial\textbf
Подставив во вторую строку последнего равенства соотношение \(\Delta\textbf
Вводя единичную матрицу \(I\) и перегруппировав члены, получим соотношение
из которого находим \(\Delta\textbf
Выше, мы предполагали, что функция \(f\) не зависит явно от времени. Если же \(f\) зависит от времени явно (например, если \(f\) описывает изменяющиеся во времени внешние силы), то в уравнение \eqref
Ссылки
- D. Baraff and A. Witkin. Large steps in cloth simulation. Computer Graphics (Proc. SIGGRAPH), 1998.
- W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling. Numerical Recipes. Cambridge University Press, 1986.
Читайте также
Комментарии
Дмитрий Храмов
Компьютерное моделирование и все, что с ним связано: сбор данных, их анализ, разработка математических моделей, софт для моделирования, визуализации и оформления публикаций. Ну и за жизнь немного.
Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений
Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin
Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin
Численные методы решения задачи Коши
Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
Идея численных методов решения задачи (3), (4) состоит из четырех частей:
1. Вводится расчетная сетка по переменной \( t \) (время) из \( N_t + 1 \) точки \( t_0 \), \( t_1 \), \( \ldots \), \( t_
2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.
3. Аппроксимируем производные конечными разностями.
4. Формулируем алгоритм, который вычисляет новые значения \( \pmb
Явный метод Эйлера
Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами \( t_n \) и \( t_
Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb
Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$
В произвольном узле сетки \( t_n \) это определение можно переписать в виде: $$ \begin
Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение \( y^n \) для того, чтобы решить уравнение (5) относительно \( y^
При условии, что у нас известно начальное значение \( \pmb
Программная реализация явного метода Эйлера
Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом
При решении системы (векторный случай), u[n] — одномерный массив numpy длины \( m+1 \) (\( m \) — размерность задачи), а функция F должна возвращать numpy -массив размерности \( m+1 \), t[n] — значение в момент времени \( t_n \).
Таким образом численное решение на отрезке \( [0, T] \) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.
Функция euler решения системы уравнений реализована в файле euler.py:
Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .
Неявный метод Эйлера
При построении неявного метода Эйлера значение функции \( F \) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin
Таким образом для нахождения приближенного значения искомой функции на новом временном слое \( t_
Для решения уравнения (8) можно использовать, например, метод Ньютона.
Программная реализация неявного метода Эйлера
Функция backward_euler решения системы уравнений реализована в файле euler.py:
Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .
Методы Рунге—Кутта
Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin
Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin
Многошаговые методы
В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах \( \pmb
Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin
Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции \( \pmb
Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен \( m+1 \).
Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям \( \pmb
Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет \( m \)-ый порядок.
На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb
Жесткие системы ОДУ
При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке \( u = w \) передаются линейной системой $$ \begin
Пусть \( \lambda_i(t) \), \( i = 1, 2, \ldots, m \) — собственные числа матрицы $$ \begin
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование \( A \)-устойчивых или \( A(\alpha) \)-устойчивых методов.
Метод называется \( A \)-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ \begin
Неявный метод эйлера для решения дифференциальных уравнений
Pers.narod.ru. Обучение. Лекции по численным методам. Численное решение обыкновенных дифференциальных уравнений
5. Численное решение обыкновенных дифференциальных уравнений
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:
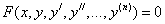
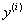
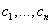
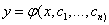
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n=1 можно говорить только о задачи Коши.
Примеры постановки задачи Коши:
Примеры краевых задач:
Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.
Численные методы решения задачи Коши для ОДУ первого порядка
Постановка задачи. Найти решение ОДУ первого порядка
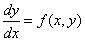
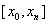
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом 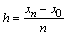
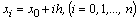
Целью является построение таблицы
т.е. ищутся приближенные значения y в узлах сетки.
Интегрируя уравнение на отрезке 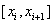
Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка
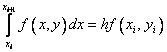
то получим явную формулу Эйлера:
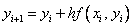
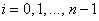
Зная 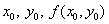
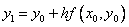
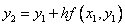
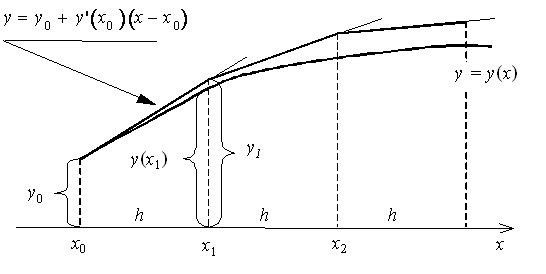
Геометрическая интерпретация метода Эйлера:
Пользуясь тем, что в точке x0 известно решение y(x0) = y0 и значение его производной 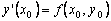
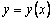
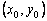
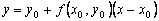
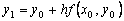
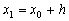
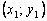
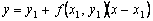
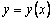
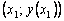
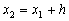
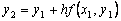
Явный метод Эйлера имеет первый порядок точности или аппроксимации.
Если использовать формулу правых прямоугольников: 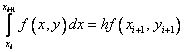
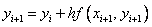
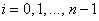
Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения 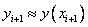
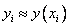
Неявный метод Эйлера имеет первый порядок точности или аппроксимации.
Модифицированный метод Эйлера: в данном методе вычисление 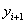
Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.
Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(xi+1) по формуле вида
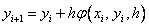
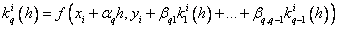
Здесь an, bnj, pn, 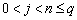
При построения методов Рунге–Кутты параметры функции 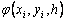
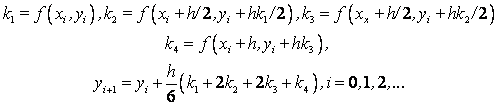
Схема Рунге – Кутта четвертого порядка точности:
Пример. Решить задачу Коши:
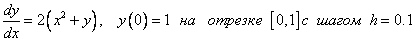
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.
Точное решение:
Расчетные формулы по явному методу Эйлера для данного примера:
Расчетные формулы модифицированного метода Эйлера:
http://slemeshevsky.github.io/num-mmf/ode/html/._ode-FlatUI001.html
http://pers.narod.ru/study/methods/05.html