Нормальное уравнение прямой. Расстояние от данной точки до данной прямой
1. Нормальное уравнение прямой
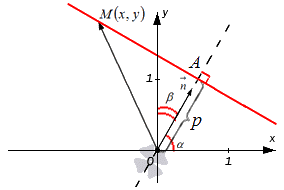
где p — длина перпендикуляра (нормали), опущенного из начала координат на прямую, а — угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель
, взятый со знаком, противоположным знаку свободного члена C.
2. Расстояние точки A(x1, y1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле
Правило. Чтобы определить расстояние точки A(x1, y1) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:
Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой.
Отклонение данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.
Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой.
Отклонение точки от прямой
В данной статье мы рассмотрим понятие отклонения точки от прямой на плоскости. Приведем примеры нахождения отклонения точки от прямой.
Отклонение точки от прямой на плоскости − это расстояние от точки до прямой, взятой со знаком «+», если эта точка и начало координат лежат по разные стороны прямой, и со знаком «−», если точка и начало координат лежат по одну сторону от прямой.
Если прямая проходит через начало координат, то отклонение точки от прямой предполагается равным расстоянию от точки до прямой, взятой со знаком «+», если точка лежит по ту сторону от прямой, куда направлен пормальный вектор прямой, и равным расстоянию от точки до прямой, взятой со знаком «−», в противном случае.
Обозначим отклонение точки от прямой символом δ, а расстояние от точки до прямой символом d. На рисунке Рис.1 отклонение точки M1 от прямой L равно δ=+d1, так как точка M1 и начало координат O лежат по разные стороны прямой L, а отклонение точки M2 от прямой L равно δ=−d2, так как точка M2 и начало координат O лежат по одну сторону от прямой L.
 |
На рисунке Рис.2 прямая L проходит через начало координат. Поэтому, отклонение точки M1 от прямой L равно δ=+d1, так как точка M1 лежит по ту сторону прямой L, куда направлен нормальный вектор n прямой L, а отклонение точки M2 от прямой L равно δ=−d2, так как точка M2 лежит по противоположную сторону прямой, куда направлен нормальный вектор n прямой L
 |
| xcosφ+ysinφ−r=0. | (1) |
где r− расстояние начала координат до прямой L, а φ− угол между нормальным вектором прямой L и осью Ox.
Покажем, что левая часть нормального уравнения прямой дает отклонение точки M(x,y) от прямой, заданной уравнением (1). Для этого докажем следующую теорему:
Теорема 1. Пусть прямая L определяется нормальным уравнением прямой (1). Тогда отклонением точки M с координатами x, y от прямой L равно δ=xcosφ+ysinφ−r.
Доказательство. Проведем через нормальный вектор прямой L линию OQ (Рис.3). Проекция точки М на прямую OQ будет точка S. Отклонение δ точки M от прямой L будет равно SR.
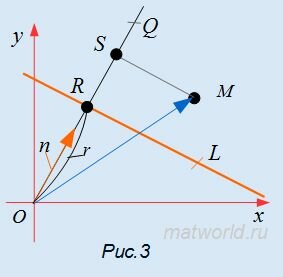 |
| δ=SR=OS−OR=OS−r. | (2) |
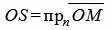 , , | (3) |
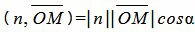 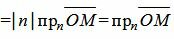 , , | (4) |
где n− единичный нормальный вектор прямой L, α−угол между векторами n и 
Из (3) и (4) следует:
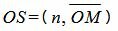 . . | (5) |
С другой стороны
 , , | (6) |
так как нормальный вектор прямой имеет координаты n=<cosφ, sinφ>, а точка M − M(x, y).
Сопоставляя (2), (5) и (6), получим:
| δ=xcosφ+ysinφ−r. |
Таким образом, как следует из теоремы 1, для вычисления отклонения некоторой точки M0(x0, y0) от прямой, нужно в левую часть нормированного уравнения прямой (1) подставить координаты точки M0:
| δ=x0 cosφ+y0 sinφ−r. |
Заметим, расстояние от точки M0 до прямой L будет равно модулю отклонения данной точки от прямой.
Пример 1. Задано нормальное уравнение прямой:
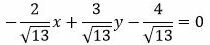 . . | (7) |
Найти отклонение точки M(5,-3) от прямой (7).
Решение. Подставим координаты точки M(5,−3) в левую часть уравнения (7):
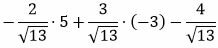 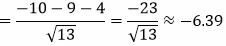 . . |
Ответ. Отклонение точки M(5,−3) от прямой (7) равно:
 . . |
Пример 2. Задано общее уравнение прямой:
Найти отклонение точки M(1,1) от прямой (8).
Решение. Один из простых методов решения − это приведение общего уравнения прямой к нормальному виду (подробнее об этом читайте в статье «нормальное уравнение прямой»). Для приведения уравнения (8) к нормальному виду, нужно умножить данное уравнение на нормирующий множитель:
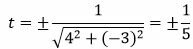 . . |
Так как в уравнении (8) третий коэффициент равен +1, то знак нормирующего множителя должен быть противоположным:
 . . |
Умножив уравнение (8) на нормирующий множитель, получим:
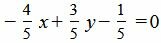 . . |
Теперь найдем отклонение точки M(1,1) от прямой (8). Для этого вставим координаты точки M в левую часть уравнения(8):
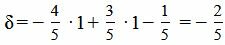 . . |
Ответ. Отклонение точки M(1,1) от прямой (8) равно:
Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .
O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .
Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p
Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y
Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.
Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .
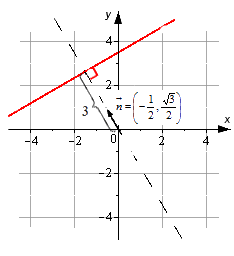
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .
Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.
Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.
Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .
Нормальное уравнение по заданной прямой найдено.
Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .
http://matworld.ru/analytic-geometry/otklonenie-tochki-ot-prjamoj.php
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnoe-normirovannoe-uravnenie-prjamoj/