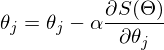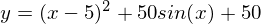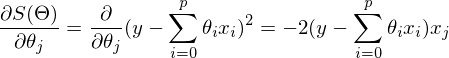Нормальное уравнение сравнение с градиентным спуском

Основы машинного обучения — часть 1 — концепция регрессии

Дата публикации Feb 23, 2018

В этой статье я вернусь к изученному материалу из удивительногокурс машинного обучения Андре Нг на Courseraи создать обзор о концепциях. Все цитаты относятся к материалу из курса, если не указано иное.

Оглавление

Определение

Говорят, что компьютерная программа извлекает уроки из опыта E в отношении некоторого класса задач T и показателя эффективности P, если ее эффективность в задачах в T, измеряемая P, улучшается с опытом E. — Том Митчелл

Линейная регрессия с одной переменной

Модельное представление

Линейная регрессия пытается подогнать точки к линии, сгенерированной алгоритмом. Эта оптимизированная линия (модель) способна прогнозировать значения для определенных входных значений и может быть нанесена на график.

Функция стоимости

Мы хотим установить параметры для достижения минимальной разницы между прогнозируемыми и реальными значениями.

Мы можем измерить точность нашей функции гипотезы, используя функцию стоимости. Для этого требуется усредненное различие (на самом деле более изощренная версия среднего) всех результатов гипотезы с входными данными из х и фактическими выходными данными у.

Градиентный спуск

Градиентный спуск продолжает изменять параметры для постепенного снижения функции стоимости. С каждой итерацией мы будем приближаться к минимуму. С каждой итерацией параметры должны быть адаптированы одновременно! Размер «шага» / итерации определяется параметром альфа (скорость обучения).

То, как мы это делаем, заключается в получении производной (касательной к функции) нашей функции стоимости. Наклон тангенса является производной в этой точке, и он даст нам направление движения в направлении. Мы делаем шаг вниз по функции стоимости в направлении с самым крутым спуском.

Выбор значения альфа имеет решающее значение. Если он слишком мал, алгоритм будет медленным, если он слишком большой, он не сможет сходиться.

При конкретном применении к случаю линейной регрессии может быть получена новая форма уравнения градиентного спуска, где m — размер обучающего набора. Снова оба параметра должны быть обновлены одновременно.

Обратите внимание, что, хотя градиентный спуск может быть восприимчивым к локальным минимумам в целом, у задачи оптимизации, которую мы здесь поставили для линейной регрессии, есть только один глобальный и никакой другой локальный оптимумы; таким образом, градиентный спуск всегда сходится (при условии, что скорость обучения α не слишком велика) к глобальному минимуму.

Линейная регрессия с несколькими переменными

Теперь вместо одной функции / переменной, которая отвечает за определенный результат, у нас есть несколько.

Следовательно, гипотеза изменяется соответствующим образом и принимает во внимание несколько параметров. То же относится и к градиентному спуску. Это просто расширение за счет дополнительных параметров, которые должны быть обновлены.

Масштабирование функций и нормализация среднего

Чтобы убедиться, что все значения объектов находятся в одном масштабе и имеют одинаковое значение, необходимо использовать Масштабирование объектов и Среднюю нормализацию.

Масштабирование признаков включает деление входных значений на диапазон (т. Е. Максимальное значение минус минимальное значение) входной переменной, в результате чего новый диапазон составляет всего 1. Средняя нормализация включает в себя вычитание среднего значения для входной переменной из значений для этого входная переменная, приводящая к новому среднему значению для входной переменной, равному нулю.

Скорость обучения

Чтобы выбрать подходящую скорость обучения, градиентный спуск должен быть нанесен и «отлажен».

Составьте график с количеством итераций по оси X. Теперь нарисуйте функцию стоимости J (θ) по числу итераций градиентного спуска. Если J (θ) когда-либо увеличивается, то вам, вероятно, нужно уменьшить α.

Если J (0) перестает существенно уменьшаться на шаге итерации, может быть объявлена ​​сходимость.

Полиномиальная регрессия

Возможности могут быть улучшены путем переопределения функции гипотезы в функцию квадратичного, кубического или квадратного корня.

В этом случае, дополнительное масштабирование должно применяться к масштабированию объектов!

Нормальное уравнение (для аналитических вычислений)

Вместо использования градиентного спуска для постепенной минимизации функции стоимости нормальное уравнение устанавливает нулевые производные

Нормальное уравнение не требует альфа-скорости обучения и никакой итерации вообще, но требует транспонирования матрицы проекта. При наличии большого количества объектов (например, 10000) расчет займет больше времени, чем итерационный процесс с градиентным спуском. Для улучшения качества нормального уравнения функции алгоритма должны быть упорядочены, а избыточные элементы удалены.

Логистическая регрессия

классификация

Для классификации данных результат должен быть 0 или 1 (двоичная классификация). С точки зрения регрессии это может означать классификацию выходных данных, то есть> 0,5 как 1, а выходных данных

Возвращает вероятность для выхода 1!

Адаптированная функция стоимости и градиентный спуск

Из-за использования сигмоидальной функции, функция стоимости должна быть соответствующим образом адаптирована с использованием логарифма. Поскольку цель теперь состоит не в том, чтобы минимизировать расстояние от прогнозируемого значения, а в том, чтобы минимизировать расстояние между выходными данными по гипотезе и y (0 или 1).

Или для векторизованной реализации:

Однако, градиентный спуск остается тем же, потому что формула использует производную часть гипотезы!

Или для векторизованной реализации:

Альтернативы градиентному спуску

Более сложные алгоритмы оптимизации, такие как

часто позволяют более быстрые вычисления без необходимости выбирать альфа-скорость обучения.

Мультиклассовая классификация

Ранее описанное решение проблемы классификации работает только для двоичной классификации. Наличие большего возможного результата, чем n = 2, называется мультиклассовой классификацией. Чтобы применить концепцию к нескольким классам, используется метод «один против всех», который по существу применяет двоичную классификацию для каждого класса (один класс положительный, все остальные отрицательные). Вместо установки y в 0 или 1, y устанавливается в i, что само по себе проверяется на всех остальных классах. В основном процесс состоит из двух частей:

1. Установка логистического классификатора на y. (если у 3, мы создаем 3 классификатора)
2. Новый вход проверяется на соответствие всем классификаторам и выбирается с наибольшей вероятностью.

Проблема переоснащения и использования регуляризации

В случае переоснащения модель идеально фиксирует структуру данных, тогда как при недостаточном подборе модели фиксируется недостаточно структуры данных (т. Е. График модели едва касается всех точек данных).

Чтобы решить проблему переоснащения, можно уменьшить либо характеристики, либо величину их значений можно упорядочить.

регуляризация

Для регуляризации модели необходимо добавить параметр (лямбда) к функции стоимости. Это де- или раздувает параметр Theta.

Следовательно, применение его к логистической регрессии выглядит так:

Обратите внимание, что параметр регуляризации начинается с 1, а не регуляризациитермин смещения Theta 0,

Это завершает первую часть. В следующем, нейронные сети будут описаны. Следите за обновлениями!

Около

Я считаю себя решателем проблем. Мои сильные стороны — ориентироваться в сложных условиях, предлагать решения и разбивать их. Мои знания и интересы связаны с бизнес-правом и программированием приложений машинного обучения. Я предоставляю услуги по анализу данных и оценке связанных с бизнесом концепций.

Математика для искусственных нейронных сетей для новичков, часть 2 — градиентный спуск

В первой части я забыл упомянуть, что если случайно сгенерированные данные не по душе, то можно взять любой подходящий пример отсюда. Можно почувствовать себя ботаником, виноделом, продавцом. И все это не вставая со стула. В наличии множество наборов данных и одно условие — при публикации указывать откуда взял данные, чтобы другие смогли воспроизвести результаты.

Градиентный спуск

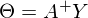
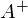
В прошлой части был показан пример вычисления параметров линейной регрессии с помощью метода наименьших квадратов. Параметры были найдены аналитически — , где — псевдообратная матрица. Это решение наглядное, точное и короткое. Но есть проблема, которую можно решить численно. Градиентный спуск — метод численной оптимизации, который может быть использован во многих алгоритмах, где требуется найти экстремум функции — нейронные сети, SVM, k-средних, регрессии. Однако проще его воспринять в чистом виде (и проще модифицировать).

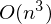
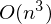
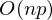
Проблема заключается в том, что вычисление псевдообратной матрицы очень затратно: 2 умножения по , нахождение обратной матрицы — , умножение матрицы вектор , где n — количество элементов в матрице A (количество признаков * количество элементов в тестовой выборке) Если количество элементов в матрице A велико (> 10^6 — например), то даже если в наличии 10000 ядер, нахождение решения аналитически может затянуться. Также первая производная может оказаться нелинейной, что усложнит решение, аналитического решения может не оказаться вовсе или данные могут просто не влезть в память и потребуется итеративный алгоритм. Бывает, что в плюсы записывают и то, что численное решение не идеально точное. В связи с этим функцию стоимости минимизируют численными методами. Задачу нахождения экстремума называют задачей оптимизации. В этой части я остановлюсь на методе оптимизации, который называется градиентный спуск.

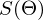
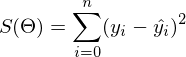
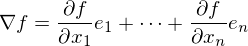
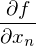
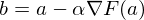
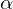
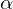
Не будем отходить от линейной регрессии и МНК и обозначим функцию потерь как — она осталась неизменной. Напомню, что градиент — это вектор вида , где — это частная производная. Одним из свойств градиента является то, что он указывает направление, в котором некоторая функция f возрастает больше всего. Доказательство этого следует из определения производной. Пара доказательств. Возьмем некоторую точку a — в окрестности этой точки функция F должна быть определена и дифференцируема, тогда вектор антиградиента будет указывать на направление, в котором функция F убывает быстрее всего. Отсюда делается вывод, что в некоторой точке b, равной , при некотором малом значение функции будет меньше либо равным значению в точке а. Можно представить это, как движение вниз по холму — сделав шаг вниз, текущая позиция будет ниже, чем предыдущая. Таким образом, на каждом следующем шаге высота будет как минимум не увеличиваться. Формальное определение. Исходя из этих определений можно получить формулу для нахождения неизвестных параметров (это просто переписанная версия формулы выше):

— это шаг метода. В задачах машинного обучения его называют скоростью обучения.

Метод очень прост и интуитивен, возьмем простой двумерный пример для демонстрации:

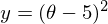
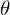
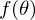
Необходимо минимизировать функцию вида . Минимизировать значит найти при каком значении функция принимает минимальное значение. Определим последовательность действий:

1) Необходима производная по :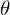
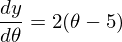
2) Установим начальное значение 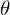= 0
3) Установим размер шага — попробуем несколько значений — 0.1, 0.9, 1.2, чтобы посмотреть как этот выбор повлияет на сходимость.
4) 25 раз подряд выполним указанную выше формулу: 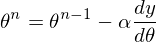Так как неизвестный параметр только один, то и формула только одна.

Код крайне прост. Исключая определение функций, весь алгоритм уместился в 3 строки:

Весь процесс можно визуализировать примерно так (синяя точка — значение на предыдущем шаге, красная — текущее):

Или же для шага другого размера:

При значении, равном 1.2, метод расходится, каждый шаг опускаясь не ниже, а наоборот выше, устремляясь в бесконечность. Шаг в простой реализации подбирается вручную и его размер зависит от данных — на каких-нибудь ненормализованных значениях с большим градиентом и 0.0001 может приводить к расхождению.

Вот еще пример с «плохой» функцией. В первой анимации метод также расходится и будет долго блуждать по холмам из-за слишком высокого шага. Во втором случае был найден локальный минимум и варьируя значение скорости не получится заставить метод найти минимум глобальный. Этот факт является одним недостатков метода — он может найти глобальный минимум только если функция выпуклая и гладкая. Или если повезет с начальными значениями.

Плохая функция:

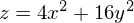
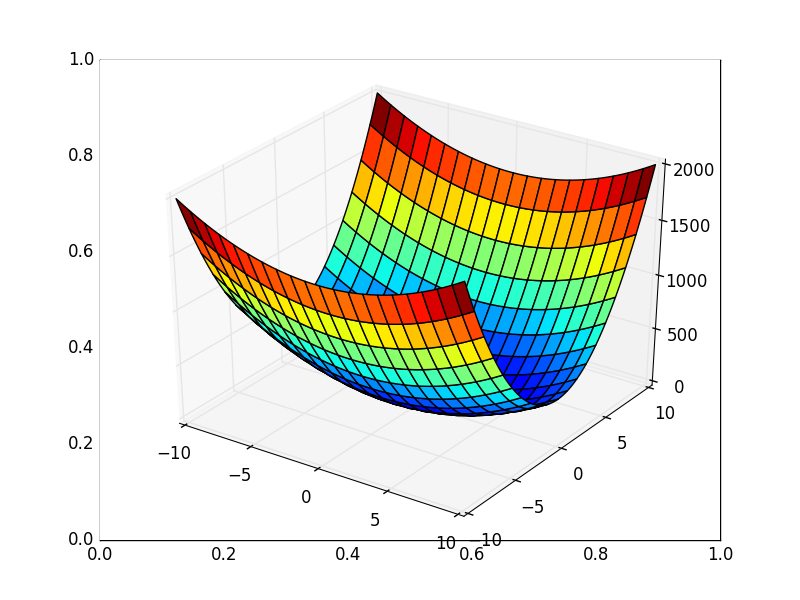
Также возможно рассмотреть работу алгоритма на трехмерном графике. Часто рисуют только изолинии какой-то фигуры. Я взял простой параболоид вращения: . В 3D выглядит он так: , а график с изолиниями — «вид сверху».

Также обратите внимание, что все линии градиента, направлены перпендикулярно изолиниям. Это означает, что двигаясь в сторону антиградиента, не получится за один шаг сразу же прыгнуть в минимум — градиент указывает совсем не туда.

После графического пояснения, найдем формулу для вычисления неизвестных параметров 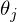линейной регрессии с МНК.

Если бы количество элементов в тестовой выборке было равно единице, то формулу можно было бы так и оставить и считать. В случае, когда в наличии n элементов алгоритм выглядит так:

Повторять v раз
<

для каждого j одновременно.
>, где n — количество элементов в обучающей выборке, v — количество итераций

Требование одновременности означает, что производная должна быть вычислена со старыми значениями theta, не стоит вычислять сначала отдельно первый параметр, затем второй и т.д., потому что после изменения первого параметра отдельно, производная также изменит свое значение. Псевдокод одновременного изменения:

Если вычислять значения параметров по одиночке, то это уже будет не градиентный спуск. Допустим, у нас трехмерная фигура и если вычислять параметры один за одним, то можно представить этот процесс как движение только по одной координате за раз — один шажок по x координате, затем шажок по y координате и т.д. ступеньками, вместо движения в сторону вектора антиградиента.

Приведенный выше вариант алгоритма называют пакетный градиентный спуск. Количество повторений можно заменить на фразу «Повторять, пока не сойдется». Эта фраза означает, что параметры будут корректироваться до тех пор, пока предыдущее и текущее значения функции стоимости не сравняются. Это значит, что локальный или глобальный минимум найден и дальше алгоритм не пойдет. На практике равенства достичь невозможно и вводится предел сходимости . Его устанавливают какой-нибудь малой величиной и критерием остановки является то, что разность предыдущего и текущего значений меньше предела сходимости — это значит, что минимум достигнут с нужной, установленной точностью. Выше точности (меньше ) — больше итераций алгоритма. Выглядит это как-то так:

Так как пост неожиданно растянулся, я бы хотел его на этом завершить — в следующей части я продолжу разбор градиентного спуска для линейной регрессии с МНК.

Градиентный спуск и метод нормальных уравнений для решения линейной регрессии дают различные решения

я работаю над проблемой машинного обучения и хотите использовать линейную регрессию в качестве алгоритма обучения. Я реализовал 2 разных метода поиска параметров theta модели линейной регрессии: градиентный (самый крутой) спуск и нормальное уравнение. На одних и тех же данных они оба должны давать примерно равные theta вектор. Однако они этого не делают.

и theta векторы очень похожи на все элементы, кроме первого. Это тот, который используется для умножения вектора всех 1 добавленных данных.

вот как theta S выглядит так (первый столбец-выход градиентного спуска, второй выход нормального уравнения):

что может вызвать разницу в theta(1, 1) возвращается градиентным спуском по сравнению с theta(1, 1) возвращается нормальным уравнением? У меня есть ошибка в коде?

вот моя реализация нормального уравнения в Matlab:

вот код для градиентного спуска:

I передайте точно такие же данные X и y для обеих функций (я не нормализую X ).

Edit 1:

на основе ответов и комментариев я проверил несколько мой код и запустить некоторые тесты.

сначала я хочу проверить, может ли проблема быть вызвана X beeing рядом с сингулярным, как предложено @user1489497 ответ. Поэтому я заменил pinv на inv-и при запуске я действительно получил предупреждение Matrix is close to singular or badly scaled. . Чтобы быть уверенным, что это не проблема я получил гораздо больший набор данных и запуск тестов с этим новым набором данных. На этот раз inv(X) не отображается предупреждение и использование pinv и inv дал такие же результаты. Так что я надеюсь, что X больше не близок к сингулярному.

затем сменил normalEque код, как предложил by щепы Итак, теперь это выглядит так:

однако проблема все еще существует. Новый normalEque функция на новых данных, которые не близко к единственному дает разные theta as gradientDesc .

чтобы узнать, какой алгоритм глючит, я запустил алгоритм линейной регрессии программного обеспечения для интеллектуального анализа данных Weka на тех же данных. Weka вычисленная тета очень похожа на выход normalEque но отличается от выхода gradientDesc . Так что я думаю, что normalEque правильная и в gradientDesc .

вот это theta s вычисляется Weka, normalEque и GradientDesc :

я также вычислял ошибки, как предложено ответ Джастина пила. Выход normalEque дает немного меньшую квадратную ошибку, но разница незначительна. Более того когда я вычисляю градиент стоимости theta С помощью функции cost (такой же, как тот, который используется gradientDesc ) у меня градиент около нуля. То же самое сделано на выходе gradientDesc не дает градиента вблизи нуля. Вот что я имею в виду:

этот предполагают, что градиентный спуск просто не сходится к глобальному минимуму. Но это вряд ли так, поскольку я запускаю его для тысяч итераций. так где же ошибка?

4 ответов

у меня наконец-то было время вернуться к этому. Нет никакого «жука».

если матрица вырождена, то существует бесконечно много решений. Вы можете выбрать любое решение из этого набора и получить одинаково хороший ответ. Решение pinv (X)*y является хорошим, что многим нравится, потому что это решение минимальной нормы.

никогда нет веской причины использовать inv (X)*y. Хуже того, использовать обратное для нормальных уравнений, таким образом, inv(X’*X)*X’*y-это просто числовое дерьмо. Я не заботьтесь, кто сказал вам использовать его, они ведут вас в неправильное место. (Да, это будет приемлемо для проблем, которые хорошо обусловлены, но большую часть времени вы не знаете, когда он собирается дать вам дерьмо. Так зачем им пользоваться?)

нормальные уравнения, как правило, плохо делать, даже если вы решаете регуляризованную проблему. Есть способы сделать это, чтобы избежать возведения в квадрат номера условия системы, хотя я не буду объяснять их, если их не спросят, поскольку этот ответ получил достаточно долго.

X\y также даст результат, который является разумным.

нет абсолютно никаких оснований бросать неограниченный оптимизатор на проблему, так как это даст результаты, которые нестабильны, полностью зависят от ваших начальных значений.

в качестве примера я начну с особой проблемы.

pinv и обратная косая черта возвращают немного разные решения. Как оказалось, есть базовое решение, к которому можно добавить любое сумма вектора nullspace для пространства строк X.

pinv генерирует решение минимальной нормы. Из всех решений, которые могли бы привести к этому, у этого есть минимум 2-норма.

напротив, обратная косая черта генерирует решение, в котором одна или несколько переменных будут равны нулю.

но если вы используете неограниченный оптимизатор, он будет генерировать решение, которое полностью зависит от ваших начальных значений. Опять же, ANLY количество этого нулевого вектора может добавьте к вашему решению, и у вас все еще есть полностью действительное решение с тем же значением суммы квадратов ошибок.

обратите внимание, что, хотя сингулярность waring не возвращается, это не означает, что ваша матрица не близка к сингулярной. Вы мало изменились в проблеме, поэтому она все еще близка, просто недостаточно, чтобы вызвать предупреждение.

Как уже говорили, плохо обусловленной матрицы гессиана, скорее всего, причиной вашей проблемы.

число шагов, которые стандартные алгоритмы градиентного спуска выполняют для достижения локального оптимума, является функцией наибольшего собственного значения гессиана, деленного на наименьшее (это известно как номер условия Гессиана). Таким образом, если ваша матрица плохо обусловлена, то для сходимости градиентного спуска к оптимуму может потребоваться чрезвычайно большое количество итераций. (Для единичный случай, он может сходиться ко многим пунктам, конечно.)

Я бы предложил попробовать три разные вещи, чтобы убедиться, что неограниченный алгоритм оптимизации работает для вашей проблемы (которая должна): 1) генерировать некоторые синтетические данные, вычисляя результат известной линейной функции для случайных входов и добавляя небольшое количество гауссовского шума. Убедитесь, что у вас гораздо больше точек данных, чем измерений. Это должно породить не-сингулярный гессиан. 2) Добавить условия регуляризации к вашей функции ошибки, чтобы увеличить номер условия гессиана. 3) Используйте метод второго порядка, такой как сопряженный градиент или L-BFGS, а не градиентный спуск, чтобы уменьшить количество шагов, необходимых для сходимости алгоритма. (Вы, вероятно, нужно сделать это в сочетании с #2).

не могли бы вы опубликовать немного больше о том, как вы X выглядит? Вы используете pinv (), который является псевдо-инверсией Мура-Пенроуза. Если матрица плохо обусловлена, это может вызвать проблемы с получением обратной. Я бы поспорил, что метод градиентного спуска ближе к отметке.

вы должны определить, какой метод на самом деле дает вам наименьшую ошибку. Это покажет, какой метод борется. Я подозреваю, что метод нормального уравнения является проблемным решением, потому что если X плохо обусловлен, тогда у вас могут быть некоторые проблемы.

вы, вероятно, должны заменить свое нормальное решение уравнения на theta = X\y который будет использовать метод QR-декомпозиции для его решения.