Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
Пусть дана некоторая прямая L. Проведём через начало координат прямую n, перпендикулярно данной и назовём её нормалью к прямой L. Буквой N отметим точку, в которой нормаль пересекает прямую L. На нормали введём направление от точки O к точке N.
Обозначим через 

будет нормальным уравнением прямой.
С помощью нормального уравнения прямой можно определить расстояние от данной точки плоскости до прямой. Пусть 

Общее уравнение прямой можно привести к нормальному виду. Пусть
— общее уравнение прямой, а
— её нормальное уравнение.
Так как оба уравнения определяют одну и ту же прямую, их коэффициенты пропорциональны.
Очевидно, для получения нормального уравнения следует все члены общего уравнения умножить на постоянный множитель 

В этой формуле берётся знак, противоположный знаку C в общем уравнении прямой.
Таким образом, получаем уравнение

которое и будет нормальным уравнением прямой на плоскости.
Пример 1. Привести общее уравнение прямой 
Решение. Вычисляем нормирующий множитель:

Умножаем все члены общего уравнения на нормирующий множитель и получаем:

Пример 2. Привести общее уравнение прямой 
Решение. Вычисляем нормирующий множитель:

Умножаем все члены общего уравнения на нормирующий множитель и получаем:

Пример 3. Найти расстояние от точки 

Решение. Приведём данное уравнение к нормальному виду. Вычисляем нормирующий множитель:

Умножаем все члены общего уравнения на нормирующий множитель и получаем нормальное уравнение:

По формуле (2) находим искомое расстояние:

Нормированное уравнение прямой
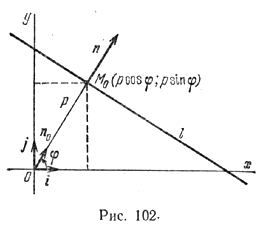
Пусть l — произвольная прямая (рис. 102).
Обозначим через p расстояние от начала координат до прямой l, а через φ — угол между осью Ох и нормальным вектором прямой l. Угол будем отсчитывать от оси Оx в направлении, противоположном движению часовой стрелки. Очевидно, что положение прямой на плоскости полностью определяется заданием величин p и φ. Выразим коэффициенты уравнения прямой l через p и φ.
Пусть M0 — точка пересечения прямой l и перпендикулярной ей прямой, проходящей через начало координат, n0 — единичный нормальный вектор прямой l, т. е. |n0| = 1. Координаты точки M0 и вектора n0 выражаются через заданные величины p и φ следующим образом:
Известно уравнение прямой, проходящей через точку (х0; у0) с нормальным вектором <А; В):
Подставив в это уравнение координаты точки M0 и вектора n0, получим
cos φ <x — p cos φ) + sin φ (у — р sin φ) = 0,
х cos φ + у sin φ — р (cos 2 φ + sin 2 φ) = 0.
В результате приходим к уравнению
х cos φ + у sin φ — р = 0.
Оно называется нормированным уравнением прямой.
В нормированном уравнении все коэффициенты имеют геометрический смысл: коэффициенты при переменных х и у — координаты единичного нормального вектора прямой; свободный член (-р) равен расстоянию от начала координат до прямой, взятому со знаком «минус». Подчеркнем еще раз, что в нормированном уравнении прямой свободный член меньше или равен нулю.
Рассмотрим, например, уравнение х — у + 5√ 2 = 0. Оно не является нормированным: вектор (1; -1) не единичный, так как | n | =√ 2 =/=1; свободный член уравнения положителен. Умножим обе части уравнения на (- 1 /√ 2 ). Тогда уравнение прямой примет вид
и станет нормированным, так как теперь вектор (- 1 /√ 2 ; 1 /√ 2 ) очевидно, единичный, а свободный член уравнения отрицателен. Нормальный вектор рассматриваемой прямой образует с осью Оx угол φ такой, что cos φ = — 1 /√ 2 , sin φ = 1 /√ 2 ,
т. е. φ = 135°. Прямая проходит на расстоянии 5 единиц длины от начала координат.
Общее уравнение прямой
всегда можно привести к нормированному виду (нормировать). Если С 0 сводится к предыдущему умножением обеих частей уравнения на -1. Поэтому, если С > 0, то за нормирующий множитель следует взять число \( -\frac<1><\sqrt
Задача. Вычислить расстояние от начала координат до прямой 6x — 8y + 25 = 0.
Тaк как С = 25 > 0, то, умножив обе части уравнения на нормирующий множитель
получим нормированное уравнение данной прямой
Учитывая геометрический смысл свободного члена нормированного уравнения прямой, видим, что искомое расстояние равно 2,5.
Нормальное уравнение плоскости
В данной статье мы рассмотрим нормальное уравнение плоскости. Приведем примеры построения нормального уравнения плоскости по углу наклона нормального вектора плоскости от осей Ox, Oy, Oz и по расстоянию r от начала координат до плоскости. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
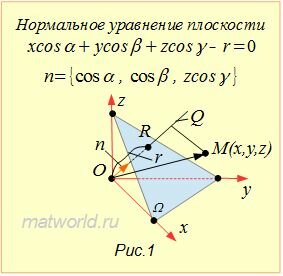
Пусть в пространстве задана декартова прямоугольная система координат. Тогда нормальное уравнение плоскости Ω представляется следующей формулой:
| xcosα+ycosβ+zcosγ−r=0, | (1) |
где r− расстояние от начала координат до плоскости Ω, а α,β,γ− это углы между единичным вектором n, ортогональным плоскости Ω и координатными осьями Ox, Oy, Oz, соответственно (Рис.1). (Если r>0, то вектор n направлен в сторону плоскости Ω, если же плоскость проходит через начало координат, то направление вектора n выбирается произвольной).
Выведем формулу (1). Пусть в пространстве задана декартова прямоугольная система координат и плоскость Ω (Рис.1). Проведем через начало координат прямую Q, перпендикулярную плоскости Ω, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 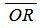
 |
Выразим уравнение плоскости Ω через следующие параметры: длину отрезка 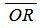
Так как вектор n является единичным вектором, то его проекции на Ox, Oy, Oz будут иметь следующие координаты:
| n=<cosα, cosβ, cosγ>. | (2) |
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M (x,y, z). Точка M лежит на плоскости Ω тогда и только тогда, когда проекция вектора 
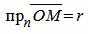 | (3) |
Скалярное произведение векторов n и 
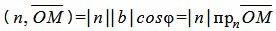 , , | (4) |
где 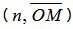


Поскольку n единичный вектор, то (4) можно записать так:
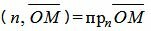 . . | (5) |
Учитывая, что n=<cosα, cosβ, cosγ>, 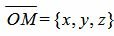
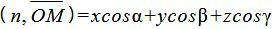 . . | (6) |
Тогда из уравнений (3), (5), (6) следует:
| xcosα+ycosβ+zcosγ=r, |
| xcosα+ycosβ+zcosγ−r=0. | (7) |
Мы получили нормальное уравнение плоскости Ω. Уравнение (7) (или (1)) называется также нормированным уравнением плоскости . Вектор n называется нормальным вектором плоскости .
Как было отмечено выше, число r в уравнении (1) показывает расстояние плоскости от начала координат. Поэтому, имея нормальное уравнение плоскости легко определить расстояние плоскости от начала координат. Для проверки, является ли данное уравнение плоскости уравнением в нормальном виде, нужно проверить длину нормального вектора этой плоскости и знак числа r, т.е. если |n|=1 и r>0, то данное уравнение является нормальным (нормированным) уравнением плоскости.
Пример 1. Задано следующее уравнение плоскости:
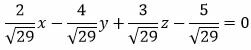 . . | (7) |
Определить, является ли уравнение (7) нормальным уравнением плоскости и если да, то определить расстояние данной плоскости от начала координат.
Решение. Нормальный вектор плоскости имеет следующий вид:
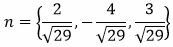 |
Определим длину вектора n:
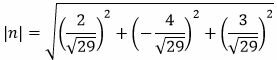 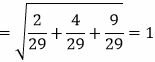 |
Ответ: Длина вектора n равна 1, 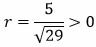
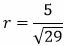
Приведение общего уравнения плоскости к нормальному виду
| Ax+By+Cz+D=0. | (8) |
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Утрерждение 2 статьи «Общее уравнение плоскости»), то существует такое число t, что
| tA=cosα, tB=cosβ, tC=cosγ, tD=−r. | (9) |
Возвышая в квадрат первые три равенства в (9) и складывая их, получим:
| (tA) 2 +(tB) 2 +(tС) 2 =cos 2 α+cos 2 β+cos 2 γ=1. | (10) |
Упростим выражение и найдем t:
| t 2 A 2 +t 2 B 2 +t 2 C 2 =t 2 (A 2 +B 2 +C 2 )=1, |
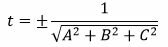 . . | (11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B, C не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на четвертое равенство в (9). Так как r−это расстояние от начала координат до плоскости, то r≥0. Тогда произведение tD должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку D.
Подставляя в (1) вместо cosα, cosβ, cosγ и −r значения из (9), получим tAx+tBy+tCz+tD=0. Т.е. для приведения общего уравенения плоскости к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем .
Пример 2. Задано общее уравнение плоскости
| 2x−3y+6z+4=0. | (12) |
Построить нормальное уравнение плоскости (12).
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=6, D=4. Вычислим t из равенства (11):
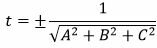 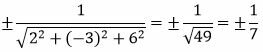 . . |
Так как D>0, то знак t отрицательный:
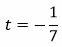 . . |
Умножим уравнение (12) на t:
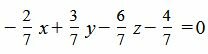 . . |
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
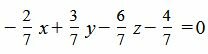 . . |
Отметим, что число 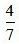
http://razdupli.ru/teor/115_normirovannoe-uravnenie-pryamoj.php
http://matworld.ru/analytic-geometry/normalnoe-uravnenie-ploskosti.php