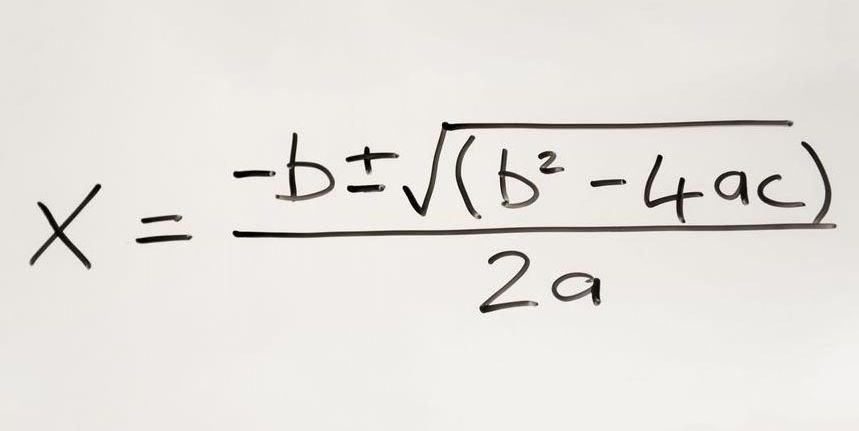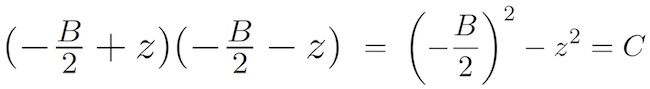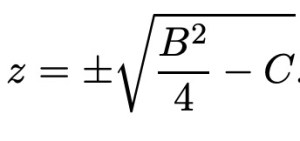Самый простой способ решения квадратичных уравнений упускается из виду в течение 4000 лет
Профессор математики открыл новый способ решения квадратных уравнений. Это вычислительно эффективнее и проще для запоминания, чем традиционная квадратичная формула. Удивительно, что такой простой метод оставался незамеченным в течение 4000 лет.
В элементарной алгебре квадратные уравнения могут быть решены с использованием различных методов, таких как факторинг, построение графиков, построение квадратов и другие.
История квадратичной формулы — формула обеспечивает решение (я) квадратного уравнения — может быть прослежена до древне-вавилонского периода около 2000–1600 гг. До н.э. Многие великие математики оставили свой след на этом предмете, и формула стала одной из самых важных частей в алгебре.
Формула, однако, довольно сложна, и ее вычисления несколько запутаны. Это может быть сложной задачей для начинающих изучающих алгебру.
Недавно математик из Университета Карнеги-Меллона в Питтсбурге опубликовал более простое решение для любого квадратного уравнения. Этот новый метод прост в запоминании и эффективен в вычислительном отношении.
По словам его автора, По-Шен Ло , он имеет потенциал для демистификации квадратичной формулы для студентов во всем мире.
Альтернативный метод решения квадратичных задач
Самый первый шаг — посмотреть, можно ли разложить квадратное уравнение следующим образом:
Если факторизация возможна, то квадратичная функция равна нулю при X=R или X=S. Согласно традиционному методу, если сумма и произведение R и S равно -B и C соответственно, то
А вот теперь начинается поворот.
Два числа суммируют с -B именно тогда, когда их среднее значение равно -B / 2. Рассмотрим эти два числа в виде -B / 2 ± z, где z — неизвестная величина, а произведение этих чисел равно C.
Если z оказывается равным нулю, то мы разложим с R = S = (- B / 2), в противном случае,
Квадратный корень всегда существует (с учетом комплексных чисел), поэтому искомые R и S всегда существуют для любого квадратичного уравнения. Таким образом, исходные корни могут быть выражены как
А, это новая квадратичная формула; гораздо проще и легче запомнить, чем предыдущий.
Почему сейчас?
Новый метод интуитивно понятен и не требует запоминания формулы вообще. Однако, более интересный вопрос, почему никто не думал об этом раньше.
Автор исследовал 4000-летнюю историю по этой теме: он изучал различные подходы, построенные древними вавилонянами, греками, индийцами, арабами и китайцами, а также современными математиками, но не нашел ничего похожего на его метод.
По-Шен Ло считает, что это связано с тем, как традиционный метод доказывает, что квадратные уравнения имеют два корня. Обычно считается, что квадратное уравнение всегда имеет два корня, и эти корни имеют произведение C и -B.
Возможно, к тому времени, когда математика продвинулась до «приличного уровня», Вавилонская техника исчезла из недавней памяти, и люди нашли подход завершения квадрата достаточно хорошим, чтобы интегрироваться в основную учебную программу.
Теперь вопрос в том, как быстро и насколько широко он будет распространяться.
Теоретический материал по теме «10 способов решений квадратных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
10 способов решения квадратных уравнений
Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Многие практические задачи решаются с их помощью. Например, квадратное уравнение позволяет рассчитать тормозной путь автомобиля, мощность ракеты для вывода на орбиту космического корабля, траектории движения различных физических объектов – от элементарных частиц до звёзд.
В школе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения. Предлагаю 10.
Определение 1. Квадратным уравнением называют уравнение вида ах 2 + b х + с = 0, где коэффициенты а, в, с- действительные числа, а ≠ 0.
Определение 2 . Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых т.е. коэффициенты в и с отличны от нуля.
Неполное квадратное уравнение — это уравнение, в котором хотя бы один из коэффициентов в или, с равен нулю.
Определение 3. Корнем квадратного уравнения ах 2 + вх + с = 0 называют всякое значение переменной х, при котором квадратный трехчлен ах 2 + вх + с обращается в нуль.
Определение 4 . Решить квадратное уравнение — значит найти все его
корни или установить, что корней нет.
Разложение левой части уравнения на множители.
Решим уравнение х 2 + 10х — 24 = 0 .
Разложим левую часть на множители:
х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
Произведение множителей равно нулю, если по крайней мере, один из его множителей равен нулю.
х + 12= 0 или х – 2=0
2. Метод выделения полного квадрата двучлена.
Решим уравнение х 2 + 6х — 7 = 0 .
Выделим в левой части полный квадрат:
тогда, данное уравнение можно записать так:
х + 3=4 или х + 3 = -4
3.Решение квадратных уравнений по формулам.
а) Решим уравнение:
б) Решим уравнение:
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
Данное уравнение корней не имеет.
Ответ: корней нет.
4. Решение уравнений с использованием теоремы Виета.
Чтобы квадратное уравнение привести к приведенному виду, нужно все его члены разделить на a ,, тогда
сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
5. Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
Умножая обе его части на а, получаем уравнение а 2 х 2 + а b х + ас = 0.
Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению у 2 + by + ас = 0,
Его корни у 1 и у 2 найдем с помощью теоремы Виета и окончательно:
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 2х 2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
Согласно теореме Виета
6. Свойства коэффициентов квадратного уравнения.
1. Пусть дано квадратное уравнение ах 2 + b х + с = 0, где а ≠ 0.
Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю),
А. Решим уравнение 345х 2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
Б. Решим уравнение 132х 2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
2) Решим уравнение 2х 2 + 3х +1= 0. Так как 2 — 3+1=0, значит х 1 = — 1, х 2 = -с/а= -1/2
Данный метод удобно применять к квадратным уравнениям с большими коэффициентами.
2. Если второй коэффициент уравнения b = 2 k – четное число, то формулу корней можно записать в виде
Решим уравнение 3х 2 — 14х + 16 = 0 .
Приведенное уравнение х 2 + рх + q = 0 совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней принимает вид
Формулу ( ) удобно использовать, когда р — четное число.
Пример. Решим уравнение х 2 – 14х – 15 = 0.
Решение. Имеем а=1, в =-14, (к=-7),с=-15.
7.Графическое решение квадратного уравнения.
И спользуя знания о квадратичной и линейной функциях и их графиках, можно решить квадратное уравнение так называемым функционально-графическим методом. Причем некоторые квадратные уравнения можно решить различными способами, рассмотрим эти способы на примере одного квадратного уравнения.
Пример. Решить уравнение =0
1способ . Построим график функции , воспользовавшись алгоритмом.
Значит, вершиной параболы служит точка (1;-4), а осью параболы – прямая x=1
2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки рис.2
х= -1 и х=3, тогда f (-1)= f (3)=0.
3) Через точки (-1;0) , (1;-4), (3;0) проводим параболу (рис 2).
Корнями уравнений являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения
Преобразуем уравнение к виду .
Построим в одной системе координат графики функций и (рис 3 ).
Они пересекаются в двух точках A(-1;1) и B(3;9). Корнями уравнения служат абсциссы точек A и B , значит, .
3 способ
Преобразуем уравнения к виду.
Построим в одной системе координат графики функций и (рис.4) Они пересекаются в двух точках A(-1;-2) и В (3;6). Корнями уравнения являются абсциссы точек А и В, поэтому .
Преобразуем уравнение к виду , затем т.е.
Построим в одной системе координат параболу и прямую . Они пересекаются в точках А(-1;4) и В(3;4). Корнями уравнений служат абсциссы точек А и В, поэтому (рис.5) .
Рис.5
Разделим почленно обе части уравнения на x, получим:
Построим в одной системе координат гиперболу и прямую (рис.6). Они пересекаются в двух точках А(-1;-3) и В(3;1). Корнями уравнений являются абсциссы точек А и В, следовательно, .
Первые четыре способа применимы к любым уравнениям вида
ах 2 + b х + с = 0, а пятый- только к тем, у которых с не равно нулю.
Графические способы решения квадратных уравнений красивы, но не дают стопроцентной гарантии решения любого квадратного уравнения.
8. Решение квадратных уравнений с помощью циркуля и
Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + b х + с = 0 с помощью циркуля и линейки (рис.7 ).
Допустим, что искомая окружность пересекает ось
Центр окружности находится в точке пересечения перпендикуляров SF и SK , восстановленных в серединах хорд AC и BD , поэтому
Итак:
1) построим точки (центр окружности) и A (0; 1) ;
2) проведем окружность с радиусом SA ;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
2) Радиус окружности равен ординате центра ( AS = SB , или R = a + c /2 a ) , окружность касается оси Ох (рис.8б) в точке В(х 1 ; 0) , где х 1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра
окружность не имеет общих точек с осью абсцисс (рис 8в), в этом случае уравнение не имеет решения.
Решим уравнение х 2 — 2х — 3 = 0 (рис.9).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA , где А (0; 1).
9. Решение квадратных уравнений с помощью
Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
Таблица XXII . Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-

Криволинейная шкала номограммы построена
по формулам (рис.10):
Полагая ОС = р, ED = q , ОЕ = а (все в см.), из
подобия треугольников САН и CDF получим
откуда после подстановок и упрощений вытекает уравнение
причем буква z означает метку любой точки криволинейной шкалы.
2) Решим с помощью номограммы уравнение
Разделим коэффициенты этого уравнения на 2,
3) Для уравнения z 2 — 25 z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5 t , получим уравнение t 2 — 5 t + 2,64 = 0,
10. Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
1) Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.12).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD , достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25) , т.е. S = х 2 + 10х + 25. Заменяя
х 2 + 10х числом 39 , получим, что S = 39 + 25 = 64 , откуда следует, что сторона квадрата ABCD , т.е. отрезок АВ = 8 . Для искомой стороны х первоначального квадрата получим
2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0 .
Решение представлено на рис 13. где
Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой
один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у 1 = 2, у 2 = — 8 (рис. .
3) Решить геометрически уравнение у 2 — 6у — 16 = 0.
Преобразуя уравнение, получаем
На рис 14. находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3 . Значит, если к выражению у 2 — 6у прибавить 9 , то получим площадь квадрата со стороной у — 3 . Заменяя выражение у 2 — 6у равным ему числом 16,

http://infourok.ru/teoreticheskij-material-po-teme-10-sposobov-reshenij-kvadratnyh-uravnenij-4034975.html