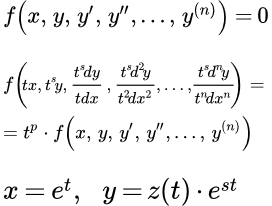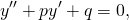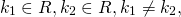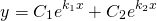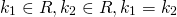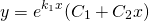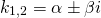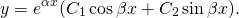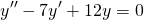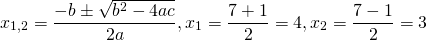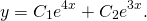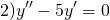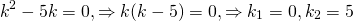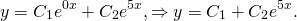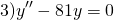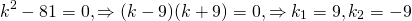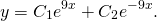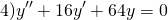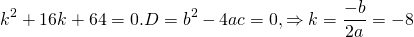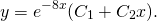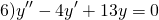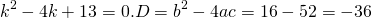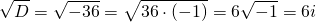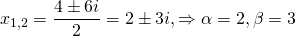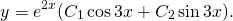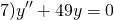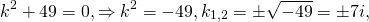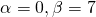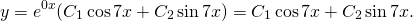Обобщенное однородное дифференциальное уравнение 2 порядка

Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков

Определения однородных уравнений и функций

Ранее мы рассматривали дифференциальные уравнения высших порядков, однородные относительно функции и ее производных. Теперь рассмотрим уравнения, однородные относительно переменных. Эти уравнения не меняют вид, если сделать замену
,
где t – постоянная. Однако мы немного усложним задачу, и будем рассматривать уравнения, которые не меняют вид при замене
(1) .
При этом производная порядка m умножается на :
.
Такие уравнения называются обобщенными однородными дифференциальными уравнениями высших порядков относительно переменных. Число s называют измерением однородности для переменной y .

Функция, зависящая от производных и переменных, называется обобщенно однородной относительно переменных, если она обладает следующим свойством:
(2) ,
где t – произвольное выражение;
Коэффициент p называется показателем однородности функции. Его также называют измерением однородности функции f .

Таким образом, если у нас имеется дифференциальное уравнение
(3) ,
и при этом функция f обладает свойством (2), то такое уравнение является обобщенно однородным относительно переменных. Действительно, выполнив замену (1) в уравнении (3), и воспользовавшись (2), имеем:
;
;
.
Постоянная t сократилась. Значит это обобщенно однородное уравнение относительно переменных.

Заметим, что обобщенно однородное уравнение в общем виде можно записать так:
(4) .
Это наиболее общая форма записи уравнения, которое не меняет вид при замене (1).

При определении обобщенно однородных уравнений можно рассмотреть и более общую замену
,
введя измерение однородности k и для переменной x . Однако, если принять во внимание, что , то такая замена сводится к (1) с измерением однородности , и поэтому не дает ничего нового.

Как распознать обобщенно однородное относительно переменных дифференциальное уравнение высшего порядка

Чтобы определить, является ли дифференциальное уравнение обобщенно однородным относительно переменных, надо в уравнении выполнить следующие замены:
.
Если удастся подобрать такое число s , в результате чего t сократится, то это обобщенное однородное ДУ с измерением однородности s для переменной y .

Пример

Покажем, что следующее уравнение является обобщенно однородным:
(П1) .

Для этого делаем замену (1), и попытаемся найти такое s , при котором t сократится:
;
;
;
;
;
;
;
.
Левая часть уравнения (П1):

.
Для того, чтобы множители, содержащие t можно было вынести за скобки, они должны быть равны:
.
Отсюда
;
.
Таким образом, при все множители, содержащие t равны . Поэтому их можно сократить, в результате чего уравнение (П1) сохранит свой вид. Это означает, что уравнение (П1) является обобщенно однородным уравнением относительно переменных с измерением однородности для переменной y , . При этом функция

имеет показатель однородности (или измерение однородности ).

В заключение, приведем исходное уравнение к виду (4), выполняя преобразования.

.
Отсюда получаем уравнение
,
где .

Метод решения обобщенно однородных уравнений

Обобщенно однородное уравнение приводится к уравнению, не содержащему независимую переменную, при помощи подстановки:
(2.1) при ,
или при .
Здесь t – новая независимая переменная; – новая зависимая переменная, то есть функция от t :
.
Зависимость определяется из (2.1) в параметрическом виде.

После подстановки (2.1) в исходное уравнение, множители, содержащие переменную t , сокращаются, и мы получаем дифференциальное уравнение, не содержащее в явном виде зависимую переменную t . Далее приводится пример решения такого уравнения.

Пример

Решить уравнение:
(П2.1)

В первом примере ⇑ мы показали, что это обобщенно однородное уравнение относительно переменных с измерением однородности для переменной . Понижаем его порядок с помощью (2.1).

Поскольку в исходное уравнение входит , то оно определено при . Делаем подстановку
(П2.2) .
Здесь t – новая независимая переменная; – зависимая переменная, то есть функция от t :
.

В исходное уравнение (П2.1) входят производные и по переменной x . Выразим их через переменную t . Для этого из (П2.2) находим производные x и y по t :

.
Находим производную y по x , применяя правило дифференцирования функции, заданной параметрическим способом.
.
Тем самым мы нашли производную y по x , в параметрическом виде:
(П2.3)
Находим вторую производную y по x . Для этого дифференцируем из (П2.3) по t :

.
Снова применяем правило дифференцирования параметрической функции.
.

Подставляем , выраженные через , и производные по t в исходное уравнение (П2.1).

;
;
;
;

.
Сокращаем множитель и выполняем дальнейшие преобразования.
;
;
(П2.4) .

Мы получили дифференциальное уравнение, не содержащее зависимую переменную t в явном виде. Делаем подстановку
(П2.5) .
Теперь мы считаем, что независимой переменной является , а зависимой – u . То есть u – является функцией от :
.
Выражаем вторую производную по t через переменные и u , применяя правило дифференцирования сложной функции, и применяя (П2.5).
;
.
Подставляем в (П2.4).
.

Делим на u . При имеем:
.

В переменных и u мы получили дифференциальное уравнение первого порядка. Разделяем переменные и интегрируем.
;

Делим на . При имеем:
;
;
.
Потенцируем.
.
Раскрытие знаков модулей эквивалентно умножению на постоянную или . Заменим постоянную: .
.

Переходим к переменным t и , подставляя .
.
Разделяем переменные и интегрируем.
.

При имеем:
;
;
;
;
.
Потенцируем.
.
Заменим постоянную и выполняем преобразования.
;
.
Снова заменим постоянную .
.

Переходим к переменным x и y , используя (П2.2).

;
(П2.6) .

Теперь рассмотрим случаи ⇑, ⇑, ⇑, ⇑, которые мы исключили при выполнении операций деления.

1) Рассмотрим случай . Отсюда
– произвольная постоянная. Тогда
(П2.7) .
Подстановкой можно убедиться, что удовлетворяет уравнению (П2.4). Поэтому (П2.7) является решением исходного уравнения (П2.1).

Однако почти все решения вида (П2.7) уже включены в (П2.6) при . Из уравнения можно определить для всех C , кроме значения : . Поэтому к решению вида (П2.6) нужно добавить только одно решение (П2.7) с :
.

2) Рассмотрим случай . При этом
.
Это решение мы уже добавили.

3) Рассмотрим случай :
;
;
(П2.8) .
Можно убедиться, что удовлетворяет уравнению (П2.4). Поэтому (П2.8) является решением исходного уравнения (П2.1).

4) Рассмотрим случай . Отсюда
;
Выше мы рассмотрели более общий случай . Поэтому здесь ничего нового нет.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 19-11-2021

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Данная статья рассматривает способы решения линейных дифференциальных однородных уравнений второго порядка с постоянными коэффициентами вида y » + p y ‘ + q y = 0 с p и q являющимися действительными числами. Будет рассмотрена теория с приведением примеров с подробным решением.

Перейдем к формулировке теоремы, которая показывает, какого вида должно быть уравнение, чтобы можно было искать общее решение ЛОДУ.

Теорема общего решения линейного однородного дифференциального уравнения

Общим решением линейного однородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = 0 с непрерывными на интервале интегрирования x коэффициентами f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяют линейную комбинацию вида y 0 = ∑ j = 1 n C j · y j , где y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на интервале x , где C j , j = 1 , 2 , . . . , n берут за произвольные постоянные.

Отсюда получаем, что общее решение такого уравнения y » + p y ‘ + q y = 0 может быть записано как y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 выражаются линейно независимыми решениями, а С 1 и C 2 – произвольными постоянными. Необходимо поработать с нахождением частных решений y 1 и y 2 .

Существует формула по Эйлеру для поиска частных решений вида y = e k · x .

Если взять y = e k · x за частное решение ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 , тогда, используя подстановку, получим тождество вида:

e k · x » + p · e k · x ‘ + q · e k · x = 0 k 2 · e k · x + p · e k · x + q · e k · x = 0 e k · x · ( k 2 + p · k + q ) = 0 k 2 + p · k + q = 0

Данное тождество называют характеристическим уравнением с постоянными коэффициентами k 1 и k 2 , которые и являются его решениями и определяют частые решения вида y 1 = e k 1 · x и y 2 = e k 2 · x заданного ЛОДУ.

При различных значениях p и q можно получить характеристические уравнения с корнами такого вида:

1. Действительные и различные k 1 ≠ k 2 , k 1 , k 2 ∈ R .
2. Действительные и совпадающие k 1 = k 2 , = k 0 , k 0 ∈ R .
3. Комплексно сопряженную пару k 1 = α + i · β , k 2 = α — i · β .

Первый случай показывает, что решениями такого уравнения могут быть y 1 = e k 1 · x и y 2 = e k 2 · x , а общее решение принимает вид y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x с постоянными коэффициентами. Функции y 1 = e k 1 · x и y 2 = e k 2 · x рассматриваются, как линейно независимыми по причине отличного от нуля определителя Вронского W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 1 · x e k 2 · x k 1 · e k 1 · x k 2 · e k 2 · x = e k 1 · x · e k 2 · x · k 2 — k 1 с действительными k 1 ≠ k 2 , k 1 , k 2 ∈ R .

Второй случай объясняет, что первым частным решением функции – это выражение y 1 = e k 0 · x . Вторым частным решением можно брать y 2 = x · e k 0 · x . Определим, что y 2 = x · e k 0 · x может являться частным решением ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 и докажем линейную независимость y 1 и y 2 .

Имеем, что k 1 = k 0 и k 2 = k 0 являются совпадающими корнями характеристического уравнения. Тогда оно примет вид k — k 0 2 = 0 ⇔ k 2 — 2 k 0 · k + k 0 2 = 0 . Отсюда следует, что y » — 2 k 0 · y ‘ + k 0 2 · y = 0 является линейным однородным дифференциальным уравнением. Необходимо подставить выражение y 2 = x · e k 0 · x для того, чтобы убедиться в тождественности:

y 2 » — 2 k 0 · y ‘ 2 + k 0 2 · y 2 = 0 x · e k 0 · x » — 2 k 0 · x · e k 0 x ‘ + k 0 2 · x · e k 0 · x = 0 e k 0 · x + k 0 · x · e k 0 x ‘ — 2 k 0 · e k 0 · x + k 0 · x · e k 0 x + k 0 2 · x · e k 0 · x = 0 ( k 0 · e k 0 · x + k 0 · e k 0 · x + k 0 2 · x · e k 0 · x — — 2 k 0 · e k 0 · x — k 0 2 · x · e k 0 · x + k 0 2 · x · e k 0 · x ) = 0 0 ≡ 0

Отсюда следует, что y 2 = x · e k 0 · x — это частное решение данного уравнения. Необходимо рассмотреть линейную независимость y 1 = e k 0 · x и y 2 = x · e k 0 · x . Чтобы убедиться в этом, следует прибегнуть к вычислению определителя Вронского. Он не должен быть равен нулю.

W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 0 · x x · e k 0 · x e k 0 · x ‘ x · e k 0 · x ‘ = = e k 0 · x x · e k 0 · x k 0 · e k 0 · x e k 0 · x · ( 1 + k 0 · x ) = = e k 0 · x · e k 0 · x · 1 + k 0 · x — k 0 · x · e k 0 · x · e k 0 · x = e 2 k 0 · x ≠ 0 ∀ x ∈ R

Можно сделать вывод, что линейно независимые частные решения ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 считаются y 1 = e k 0 · x и y 2 = x · e k 0 · x . Это подразумевает то, что решением будет являться выражение y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R .

Третий случай говорит о том, что имеем дело с парой комплексных частных решений ЛОДУ вида y 1 = e α + i · β · x и y 2 = e α — i · β · x .

Запись общего решения примет вид y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x .

Функции y 1 = e a · x · cos β x и y 2 = e a · x · sin β x могут быть записаны вместо частных решений уравнения, причем с соответствующими действительной и мнимой частями. Это понятно при преобразовании общего решения y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x . Для этого необходимо воспользоваться формулами из теории функции комплексного переменного вида. Тогда получим, что

y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x = = C 1 · e α · x · cos β x + i · sin β x + C 2 · e α · x · cos β x — i · sin β x = = ( C 1 + C 2 ) · e α · x · cos β x + i · ( C 1 — C 2 ) · e α · x · sin β x = = C 3 · e α · x · cos β x + C 4 · e α · x · sin β x

Отчетливо видно, что С 3 и С 4 используются в качестве произвольных постоянных.

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения 2 порядка с постоянными переменными вида y » + p y ‘ + q y = 0 :

1. Запись характеристического уравнения k 2 + p ⋅ k + q = 0 .
2. Нахождение корней характеристического уравнения k 1 и k 2 .
3. Производим запись ЛОДУ, исходя из полученных значений с постоянными коэффициентами:

• y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x при k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R ;
• y 0 = e α · x · ( C 1 · cos β x + C 2 · sin β x ) при k 1 = α + i · β , k 2 = α — i · β .

Найти общее решение заданного уравнения с постоянными коэффициентами y » + 4 y ‘ + 4 y = 0 .

Решение

Следуя алгоритму, необходимо записать характеристическое уравнение k 2 + 4 ⋅ k + 4 = 0 , после чего обозначить его корни. Получаем, что

k 2 + 4 k + 4 = 0 ( k + 2 ) 2 = 0 k 1 = k 2 = k 0 = — 2

Очевидно, что полученные корни являются совпадающими.

Ответ: Запись общего решения: y 0 = C 1 · e k 0 x + C 2 · x · e k 0 x = C 1 · e — 2 x + C 2 · x · e — 2 x .

Найти решение заданного уравнения вида y » — 5 y ‘ + 6 y = 0 .

Решение

По условию имеется ЛОДУ 2 порядка с постоянными коэффициентами. Это указывает на то, что необходимо записать характеристическое уравнение и обозначить его корни. Получим:

k 2 — 5 k + 6 = 0 D = 5 2 — 4 · 6 = 1 k 1 = 5 — 1 2 = 2 k 2 = 5 + 1 2 = 3

Видно, что корни различные и действительные. Это говорит о том, что уравнение общего вида запишется как y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .

Ответ: y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .

Найти общее решение дифференциального уравнения вида y » — y ‘ + 3 y = 0 .

Решение

Необходимо перейти к характеристическому уравнению ЛОДУ 2 порядка, что соответствует записи k 2 — k + 3 = 0 , после чего обозначить его корни. Тогда получим, что

D = 1 2 — 4 · 3 = — 11 k 1 = 1 + i 11 2 = 1 2 + i · 11 2 k 2 = 1 — i 11 2 = 1 2 — i · 11 2 ⇒ α = 1 2 , β = 11 2

На выходе имеем пару комплексно сопряженных корней характеристического уравнения. Отсюда следует, что общим решением является запись уравнения вида

y 0 = e a · x · ( C 1 · cos β x + C 2 · sin β x ) = = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2

Ответ: y 0 = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2 .

Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид

где p и q — действительные числа. Рассмотрим на примерах, как решаются однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Решение линейного однородного однородного дифференциального уравнения второго порядка зависит от корней характеристического уравнения. Характеристическое уравнение — это уравнение k²+pk+q=0.

1) Если корни характеристического уравнения — различные действительные числа:

то общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

2) Если корни характеристического уравнения — равные действительные числа

(например, при дискриминанте, равном нулю), то общее решение однородного дифференциального уравнения второго порядка есть

3) Если корни характеристического уравнения — комплексные числа

(например, при дискриминанте, равном отрицательному числу), то общее решение однородного дифференциального уравнения второго порядка записывается в виде

Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

Найти общие решения однородных дифференциальных уравнений второго порядка:

Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.

Отсюда, общее решение этого однородного ДУ 2-го порядка есть

Составим и решим характеристическое уравнение:

Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:

В этом случае характеристическое уравнение

Корни различны и действительны. Поэтому общее решение однородного дифференциального уравнения 2-го порядка здесь

Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как

Характеристическое уравнение здесь

Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.

Общее решение этого однородного дифференциального уравнения второго порядка имеет вид

Отсюда находим общее решение данного диф. уравнения:

Примеры для самопроверки.

Найти общее решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами: